Sistemi di equazioni: 15 ESERCIZI SVOLTI
Sistemi di equazioni: 15 ESERCIZI SVOLTI! In questa pagina vedremo come risolvere i sistemi di equazioni, ed utilizzeremo i metodi principali per la risoluzione. Gli esercizi in ogni sezione sono in ordine di difficoltà, e verranno spiegati con calma in ogni singolo passaggio. Partiamo!
Indice
- Come risolvere sistemi di equazioni
- Sistemi di equazioni: esercizi col metodo di sostituzione
- Sistemi di equazioni: esercizi col metodo del confronto
- Sistemi di equazioni: esercizi col metodo di riduzione
- Sistemi di equazioni: metodo di Cramer
Diamo un attimo una panoramica generale su cosa è un sistema di equazioni, e come risolverlo in generale!
Come risolvere sistemi di equazioni
Un sistema di equazioni è un insieme di n equazioni lineari (o di primo grado) ed n incognite, quindi ad esempio avete 2 equazioni con 2 incognite (x ed y). Ci sono vari metodi per risolvere un sistema di equazioni: metodo di sostituzione, metodo del confronto, metodo di riduzione. Sono tutti equivalenti! Infatti personalmente preferisco usare sempre il metodo di sostituzione.
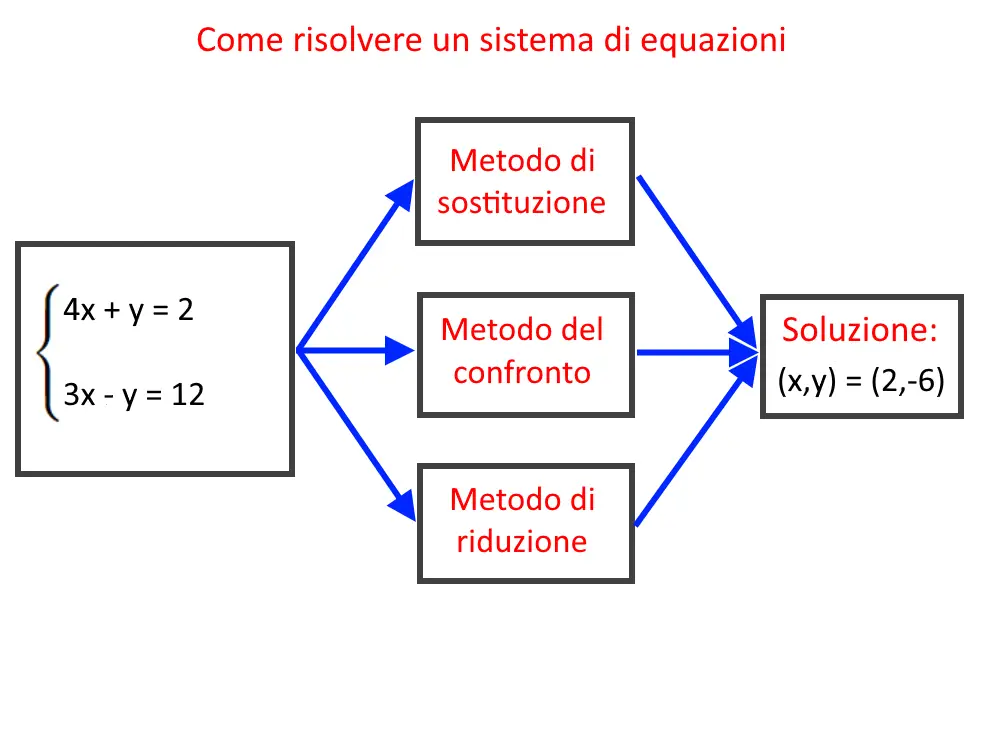
Perché è utile saper risolvere un sistema di equazioni? Il risultato, come vedete, è una coppia (x,y), ed in geometria analitica rappresenta il punto di intersezione fra due rette.
Detto questo, vediamo subito degli esercizi sui sistemi di equazioni svolti, col metodo di sostituzione!
Sistemi di equazioni: esercizi
col metodo di sostituzione
Il metodo di sostituzione consiste nel ricavare una incognita (x o y, scegliete voi, è uguale) in una delle due equazioni. Poi, tale espressione trovata la sostituiamo nell’altra equazione. A parole sembra complicato, ma basta un esempio per capire tutto!
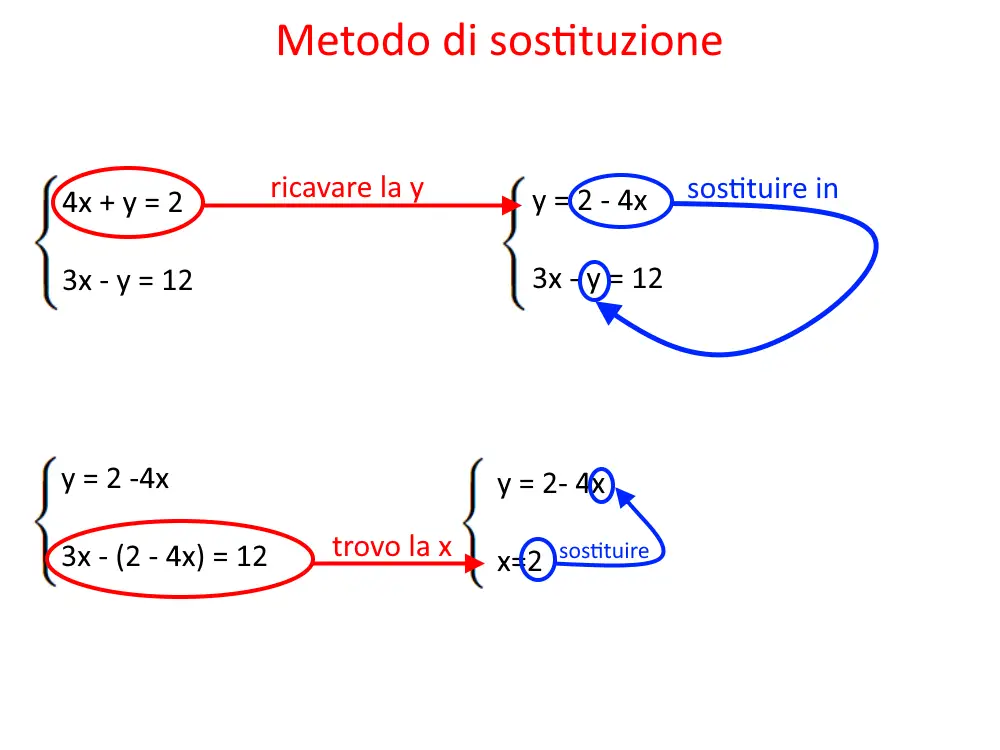
Esercizio 1. \begin{cases} x+2y = -1 \\ 5x +4y -7 = 0 \end{cases}
Nel metodo di sostituzione il primo passaggio è ricavare una incognita: x oppure y, a vostra scelta. La scelta però deve essere fatta in modo da fare meno calcoli possibili, quindi noi scegliamo, se possibile, sempre l’incognita che sta senza coefficiente vicino (quindi x da sola, o y da sola).
Nella prima equazione infatti c’è la x da sola, senza numero attaccato vicino! Quello che facciamo è rimanere la x a sinistra, e portare tutto il resto a destra, come segue.
\begin{cases} x= -1-2y \\ 5x +4y -7 = 0 \end{cases}
RICORDATE: ricavare una incognita significa trovare una espressione che contenga numeri e l’altra incognita. Ad esempio, ora ci siamo trovati x=-1-2y e va benissimo perché a destra contiene numeri e l’altra incognita y! Mentre invece NON va bene trovarsi un qualcosa del tipo x=-1-2y+2x!
A questo punto il secondo passaggio: sostituiamo l’espressione ricavata al posto della x nella seconda equazione:
\begin{cases} x= -1-2y \\ 5(-1-2y) +4y -7 = 0 \end{cases}
Abbiamo ottenuto così al secondo rigo una equazione di primo grado (contiene solo la y) che sappiamo risolvere, quindi svolgiamo prima questa, senza pensare all’altra! Il nostro obiettivo adesso è trovare la y!
\begin{cases} x= -1-2y \\ -5-10y +4y -7 = 0 \end{cases}
\begin{cases} x= -1-2y \\ -10y +4y = 7+5 \end{cases}
Sommiamo i rispettivi termini e con ultimi passaggi ci troviamo la y. Se non vi ricordate come si risolve una equazione cliccateci.
\begin{cases} x= -1-2y \\ -6y =12 \end{cases}
Come vedete, mentre risolviamo una equazione, l’altra non la tocchiamo! Questo perché dobbiamo pensare una alla volta.
\begin{cases} x= -1-2y \\ y =-2 \end{cases}
Prossimo passaggio: sostituire il valore della y trovato nell’altra equazione!
\begin{cases} x= -1-2(-2) \\ y =-2 \end{cases}
\begin{cases} x= -1+4 \\ y =-2 \end{cases}
E quindi il sistema ora è risolto:
\begin{cases} x= 3 \\ y =-2 \end{cases}
Ossia siamo riusciti a trovare sia la x, che la y! La soluzione è la coppia (3,-2).
Esercizio 2. \begin{cases} 4x-3y +1 = 0 \\ -x -2y = - \frac{5}{2} \end{cases}
Osserviamo il sistema: scegliamo una incognita soletta da ricavare…c’è la x nella seconda equazione! Il segno meno non è un problema. Ripetiamo: potete partire da dove volete, ad esempio nell’esercizio precedente siamo partiti dalla prima equazione, ora dalla seconda, è uguale. L’importante è capire il senso del procedimento.
\begin{cases} 4x-3y +1 = 0 \\ -x = 2y - \frac{5}{2} \end{cases}
A questo punto cambiando di segno, ci siamo ricavati l’espressione della x:
\begin{cases} 4x-3y +1 = 0 \\ x = -2y + \frac{5}{2} \end{cases}
Ricavata l’espressione dell’incognita x, sostituiamo tale espressione nell’altra equazione!
\begin{cases} 4(-2y + \frac{5}{2})-3y +1 = 0 \\ x = -2y + \frac{5}{2} \end{cases}
Adesso ci concentriamo sulla prima equazione, che è di primo grado e sappiamo risolvere: da essa infatti possiamo trovarci la y! Pensiamo a questa adesso!
\begin{cases} -8y + 10 -3y +1 = 0 \\ x =-2y + \frac{5}{2} \end{cases}
Portiamo la y a primo membro ed il resto a secondo:
\begin{cases} -8y -3y = -10-1 \\ x =-2y + \frac{5}{2} \end{cases}
\begin{cases} -11y = -11 \\ x =-2y + \frac{5}{2} \end{cases}
E ci troviamo finalmente il valore dalla y:
\begin{cases} y = 11 \\ x =-2y + \frac{5}{2} \end{cases}
Ora che ci siamo trovati una incognita (la y in questo caso), sostituiamo tale valore nell’altra equazione:
\begin{cases} y = 11 \\ x =-2 \cdotp 1 + \frac{5}{2} \end{cases}
\begin{cases} y = 11 \\ x =-2 + \frac{5}{2} \end{cases}
Visto che c’è una frazione, facciamo un minimo comune multiplo per trovare un numero solo:
\begin{cases} y = 1 \\ x = \frac{-4+5}{2} \end{cases}
\begin{cases} y = 1 \\ x = \frac{1}{2} \end{cases}
Il sistema ora è risolto: la soluzione è la coppia (\frac{1}{2},1) .
Esercizio 3. \begin{cases} \frac{1-x}{2} + \frac{2y+x}{3} = y \\ 3(x+y) = x-y+6 \end{cases}
Qui il discorso si complica un po’ ma il senso rimane sempre lo stesso. Noi diamo un occhio al sistema: partiamo sempre dall’equazione più semplice. La prima è con frazioni, quindi la scartiamo. La seconda appare più semplice, iniziamo da questa.
Questa volta non possiamo immediatamente ricavare una incognita, quindi svolgiamo un attimo la moltiplicazione con la parentesi e cerchiamo di renderla più semplice, in modo da trovare una delle due incognite:
\begin{cases} \frac{1-x}{2} + \frac{2y+x}{3} = y \\ 3x+3y = x-y+6 \end{cases}
Portando le x e y a primo membro, le possiamo sommare ed ottenere così una forma più semplice di tale equazione:
\begin{cases} \frac{1-x}{2} + \frac{2y+x}{3} = y \\ 3x+3y-x+y = 6 \end{cases}
\begin{cases} \frac{1-x}{2} + \frac{2y+x}{3} = y \\ 2x+4y = 6 \end{cases}
Purtroppo, come ora, non c’è una incognita soletta. Scegliamo lo stesso una incognita da ricavare, ad esempio la x:
\begin{cases} \frac{1-x}{2} + \frac{2y+x}{3} = y \\ 2x = 6-4y \end{cases}
Dividendo per 2, ci troviamo la x:
\begin{cases} \frac{1-x}{2} + \frac{2y+x}{3} = y \\ x = 3-2y \end{cases}
Ora secondo passaggio: sostituiamo l’espressione trovata nella prima equazione.
\begin{cases} \frac{1-(3-2y) }{2} + \frac{2y+3-2y}{3} = y \\ x = 3-2y \end{cases}
(Quando ci sono dei meno mettete le parentesi)
\begin{cases} \frac{1-3+2y }{2} + \frac{2y+3-2y}{3} = y \\ x = 3-2y \end{cases}
La prima è una equazione di primo grado in y, focus su questa e risolviamola!
\begin{cases} \frac{-2+2y }{2} + 1 = y \\ x = 3-2y \end{cases}
C’è una fastidiosa frazione, moltiplichiamo per il suo denominatore 2 per levarla:
\begin{cases} -2+2y + 2 = 2y \\ x = 3-2y \end{cases}
Portiamo le y a sinistra:
\begin{cases} 0y = 0 \\ x = 3-2y \end{cases}
Ciò che viene è una equazione del tipo 0y=0 e che non ha soluzione, ossia è indeterminata. Non serve andare oltre: automaticamente anche il sistema è indeterminato!
Esercizio 4. \begin{cases} -3x+2(y+5) = x+4y+1 \\ ( x- \frac{1}{2} )( x+ \frac{1}{2} ) -y = (x-1)(x+3) \end{cases}
Qui è evidente che l’equazione dove partire, ossia la più semplice è la prima! Iniziamo a svolgere qualche operazione, come levare quella parentesi, e vediamo cosa ci conviene ricavare.
\begin{cases} -3x+2y+10 = x+4y+1 \\ ( x- \frac{1}{2} )( x+ \frac{1}{2} ) -y = (x-1)(x+3) \end{cases}
\begin{cases} -3x+2y-x-4y = +1-10 \\ ( x- \frac{1}{2} )( x+ \frac{1}{2} ) -y = (x-1)(x+3) \end{cases}
Sommiamo:
\begin{cases} -4x-2y = -9 \\ ( x- \frac{1}{2} )( x+ \frac{1}{2} ) -y = (x-1)(x+3) \end{cases}
A questo punto bisogna essere furbi: se scegliamo di ricavare la x, poi dopo dobbiamo andare a sostituire nella seconda equazione per ben 4 volte! Mentre se scegliamo di ricavare la y poi dobbiamo sostituire giusto una volta dopo!
\begin{cases} -2y =4x -9 \\ ( x- \frac{1}{2} )( x+ \frac{1}{2} ) -y = (x-1)(x+3) \end{cases}
\begin{cases} y =-2x +\frac{9}{2} \\ ( x- \frac{1}{2} )( x+ \frac{1}{2} ) -y = (x-1)(x+3) \end{cases}
Espressione ricavata: andiamo a sostituire nella seconda equazione!
\begin{cases} y =-\frac{3}{2}x +\frac{9}{2} \\ ( x- \frac{1}{2} )( x+ \frac{1}{2} ) -(-2x +\frac{9}{2}) = (x-1)(x+3) \end{cases}
Compare all’inizio la differenza di quadrati, quindi usiamo tale formula.
\begin{cases} y =-\frac{3}{2}x +\frac{9}{2} \\ x^2 - \frac{1}{4} +2x -\frac{9}{2} = x^2 +3x -x -3 \end{cases}
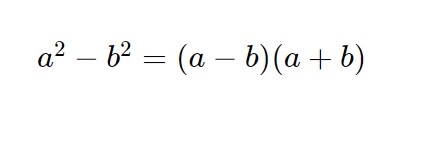
Portiamo i termini con la x a sinistra ed il resto a destra:
\begin{cases} y =-\frac{3}{2}x +\frac{9}{2} \\ x^2 +2x -x^2 -3x +x = -3 + \frac{1}{4} + \frac{9}{2} \end{cases}
I termini quadratici si levano, ed è una prova che stiamo andando bene, visto che si tratta di equazioni di primo grado.
\begin{cases} y =-\frac{3}{2}x +\frac{9}{2} \\ 2x -2x = -3 + \frac{1}{4} + \frac{9}{2} \end{cases}
A secondo membro facciamo un minimo comune multiplo:
\begin{cases} y =-\frac{3}{2}x +\frac{9}{2} \\ 0x = \frac{-12+1+18}{4} \end{cases}
\begin{cases} y =-\frac{3}{2}x +\frac{9}{2} \\ 0x = \frac{7}{4} \end{cases}
Questo è un altro caso particolare delle equazioni, ossia per qualsiasi valore di x l’equazione risulterà sempre:
0= \frac{7}{4}
(Questo perché 0 moltiplicato per qualsiasi cosa dà sempre zero)
E 0 non è uguale a sette-quarti chiaramente! Essa si dirà impossibile!
0 \ne \frac{7}{4}
Automaticamente il sistema risulta impossibile anch’esso!
Passiamo ad utilizzare il metodo del confronto negli esercizi sistemi di equazioni!
Sistemi di equazioni: esercizi
col metodo del confronto
Il metodo del confronto ha una logica abbastanza semplice: consiste nel trovare in entrambe le equazioni la y, poi uguagliare i secondi membri, ed infine risolvere l’equazione risultante. Trovata la soluzione di una incognita, bisognerà sostituire in una delle due a piacere.
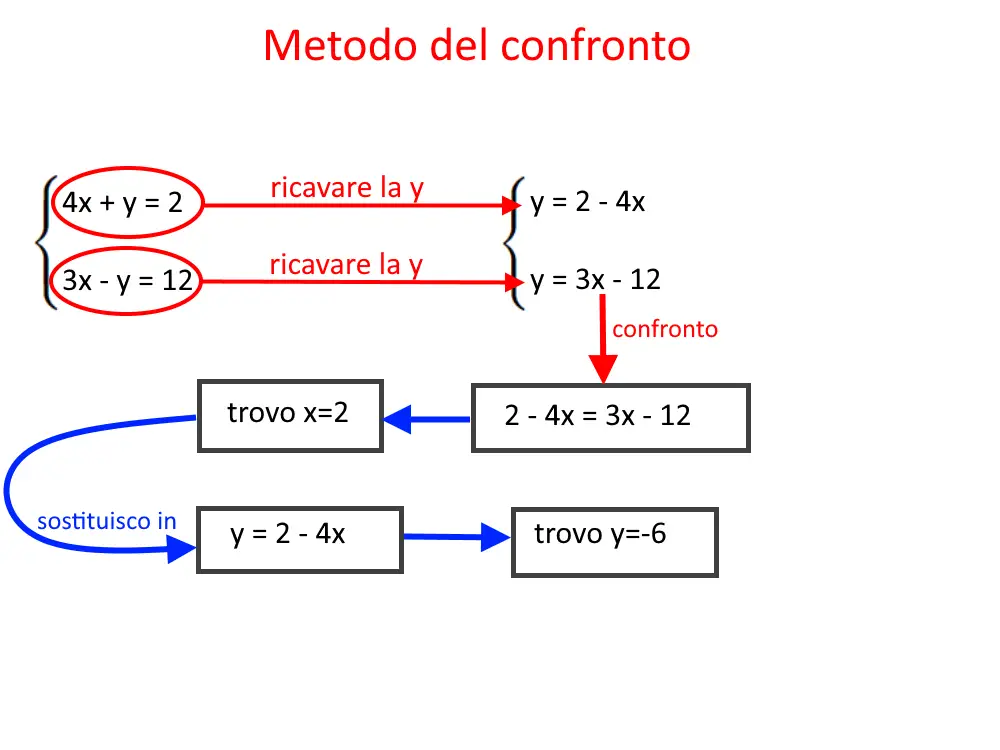
Esercizio 5. \begin{cases} 3x-2y = 7 \\ 4y = -3x-11 \end{cases}
Il metodo del confronto prevede di ricavare da entrambe le equazioni, la y! Quindi svogliamo il calcoli su entrambe le equazioni. Quello che vogliamo è avere la y da sola a sinistra.
\begin{cases} -2y =-3x+ 7 \\ 4y = -3x-11 \end{cases}
Fatto ciò, nella prima dividiamo per 2 e cambiamo di segno, e nella seconda dividiamo tutto per 4:
\begin{cases} y =\frac{3x-7}{2} \\ y = \frac{-3x-11}{4} \end{cases}
A questo punto le mettiamo a confronto: cioè inseriamo la prima espressione di y nella seconda. (Potete anche fare il contrario, a vostra scelta).
\begin{cases} y =\frac{3x-7}{2} \\ \frac{3x-7}{2} = \frac{-3x-11}{4} \end{cases}
Il secondo rigo è una equazione di primo grado che possiamo risolvere, trovando alla fine la x! Facciamolo! Moltiplichiamo tutto per 4 per eliminare le due frazioni, che rompono sempre.
\begin{cases} y =\frac{3x-7}{2} \\ 2(3x-7) = -3x-11 \end{cases}
\begin{cases} y =\frac{3x-7}{2} \\ 6x-14 = -3x-11 \end{cases}
Portiamo le x a primo membro e sommiamo:
\begin{cases} y =\frac{3x-7}{2} \\ 9x = 3 \end{cases}
\begin{cases} y =\frac{3x-7}{2} \\ x = \frac{1}{3} \end{cases}
Abbiamo trovato già una incognita, ossia la x. Adesso mettiamo questo valore nella prima equazione, e ci troviamo così anche l’altra incognita y!
\begin{cases} y =\frac{3 \frac{1}{3} -7}{2} \\ x = \frac{1}{3} \end{cases}
\begin{cases} y =\frac{1 -7}{2} \\ x = \frac{1}{3} \end{cases}
E poi, semplificando numeratore e denominatore:
\begin{cases} y = -3 \\ x = \frac{1}{3} \end{cases}
La coppia di soluzioni è stata trovata!
Esercizio 6. \begin{cases} 3x-y = 6 \\ x-2 = \frac{1}{3} y \end{cases}
La logica del metodo del confronto prevede di ricavare la y da sola a sinistra, facciamolo. La seconda equazione, essendo una uguaglianza possiamo anche invertirla (perché sinistra=destra e destra=sinistra chiaramente):
\begin{cases} -y =-3x+ 6 \\ \frac{1}{3} y = x-2 \end{cases}
Nella prima cambiamo di segno, nella seconda poi moltiplichiamo per 3:
\begin{cases} y =3x- 6 \\ y = 3x-6 \end{cases}
Il gioco è fatto! Adesso mettiamo la prima espressione nella seconda!
\begin{cases} y =3x- 6 \\ 3x- 6 = 3x-6 \end{cases}
Portando la x a sinistra, ed il -6 a destra notiamo che:
\begin{cases} y =3x- 6 \\ 0x = 0 \end{cases}
Questo 0x=0 è il caso indeterminato di una equazione. Automaticamente il sistema assume la stessa soluzione di essere indeterminato!
Esercizio 7. \begin{cases} 3x - [ - (3y-1) ] = 20 \\ 2(y-1) +x = 4 \end{cases}
Iniziamo a svolgere un po’ di calcoli per riuscire a trovare la y, ricordate che si fanno prima le parentesi tonde e poi quelle quadre dopo.
\begin{cases} 3x - [ -3y+1 ] = 20 \\ 2y-2 +x = 4 \end{cases}
Poi dopo quella quadra:
\begin{cases} 3x +3y-1 = 20 \\ 2y-2 +x = 4 \end{cases}
\begin{cases} 3y = 20 -3x+1 \\ 2y =2+ 4-x \end{cases}
E quindi otteniamo:
\begin{cases} y = \frac{21 -3x}{3} \\ y =\frac{6-x}{2} \end{cases}
Poniamo la prima espressione della prima nella seconda equazione al posto della y, come sempre.
\begin{cases} y = \frac{21 -3x}{3} \\ \frac{21 -3x}{3} =\frac{6-x}{2} \end{cases}
Moltiplichiamo per il massimo comune denominatore che è 6:
\begin{cases} y = \frac{21 -3x}{3} \\ 2(21 -3x) = 3(6-x) \end{cases}
Sciogliamo le parentesi:
\begin{cases} y = \frac{21 -3x}{3} \\ 42 -6x = 18-3x \end{cases}
E ricaviamoci la x finalmente:
\begin{cases} y = \frac{21 -3x}{3} \\ 3x-6x = -42+18 \end{cases}
\begin{cases} y = \frac{21 -3x}{3} \\ x = 8 \end{cases}
E concludiamo l’esercizio, trovando anche la y:
\begin{cases} y = \frac{21 -3\cdotp 8}{3} \\ x = 8 \end{cases}
\begin{cases} y = -1 \\ x = 8 \end{cases}
Esercizio 8. \begin{cases} x= y-4 \\ (y-2)^2 = y(y-1) + x \end{cases}
Osserviamo l’esercizio: trovare la y dalla seconda equazione sembra alquanto complicato. Il metodo del confronto può anche essere applicato con la x. Questo soprattutto quando ricavare la y sembra più difficile. Il procedimento è uguale, nel senso che portiamo a sinistra la x ed alla fine li mettiamo a confronto.
\begin{cases} x= y-4 \\ x = (y-2)^2 - y(y-1) \end{cases}
In un solo passaggio ci siamo ritrovati già ad applicare il confronto: mettiamo in uguaglianza le due espressioni, mettendo la prima nella seconda. Bisogna essere furbi ed andare sempre con calma, nessuno ci corre appresso.
\begin{cases} x= y-4 \\ y-4 = (y-2)^2 - y(y-1) \end{cases}
La seconda è una equazione di primo grado in y questa volta. Applichiamo il quadrato del binomio, che ha la seguente formula.
\begin{cases} x= y-4 \\ y-4 = y^2 + 4 - 4y - y^2 +y \end{cases}
\begin{cases} x= y-4 \\ 4y = 8 \end{cases}
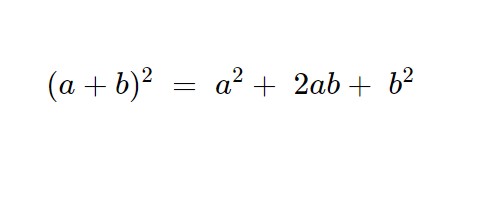
E di conseguenza:
\begin{cases} x= y-4 \\ y = 2 \end{cases}
Ricaviamo anche la x molto facilmente:
\begin{cases} x= -2 \\ y = 2 \end{cases}
Come vedete è bastato osservare il sistema, per applicare il confronto alla x, e risparmiare una gran quantità di conti e calcoli!
Andiamo avanti con gli esercizi sui sistemi di equazioni, ora utilizzando il metodo di riduzione.
Sistemi di equazioni: esercizi
col metodo di riduzione
Risolvere un sistema di equazioni col metodo di riduzione significa sommare o sottrarre fra loro le due equazioni. Questo però si applica soprattutto quando si nota che dei termini sono uguali o opposti (altrimenti non ne vale la pena fidatevi). Quindi in un solo passaggio, in questi particolari casi, si semplifica notevolmente l’esercizio.
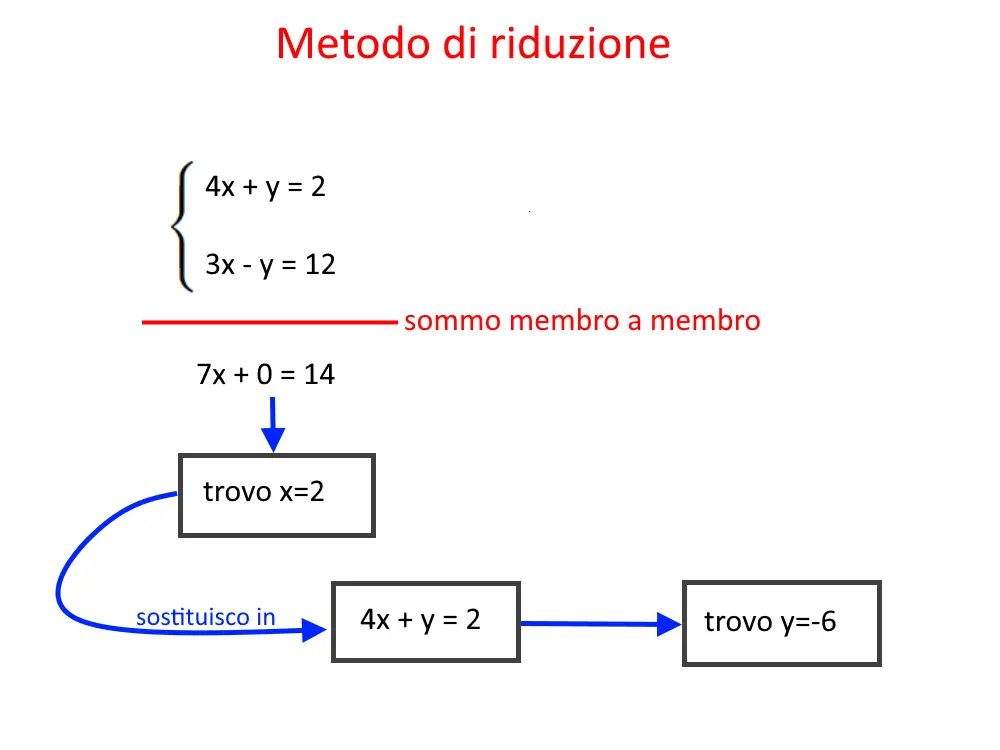
Esercizio 9. \begin{cases} 6x - y = 3 \\ -2x - y = -5 \end{cases}
Notiamo immediatamente che in entrambe le equazioni vi è un termine uguale, ossia -y. Quando si ha a che fare con termini uguali si sottrae membro a membro prima equazione meno seconda equazione. Viene fuori dalla sottrazione:
6x-(-2x) + 0 = 3- (-5)
Questa è una equazione in x, che ci permette appunto di ricavare una incognita.
6x+2x = 3+5
8x = 8 \implies x=1
In pochissimi passaggi abbiamo già ricavato una incognita! Adesso per trovare l’altra sostituiamo tale valore x=1 in una delle due: scegliamo ovviamente sempre la più semplice. La prima sembra esserlo:
6 \cdotp 1 - y = 3
- y = 3-6 \implies y=3
Con questo metodo non c’è neanche bisogno di scrivere il sistema. Si risolvono quindi due equazioni separatamente.
Esercizio 10. \begin{cases} -3x +2y = 1 \\ 3x -4y = 7 \end{cases}
Osserviamo il sistema: c’è il termine 3x e -3x che sono opposti, quindi possiamo applicare il metodo di riduzione. Essendo opposti, sommiamo membro a membro. Facciamo prima equazione + seconda equazione, viene fuori:
0 + 2y -4y = 1+7
Attenzione a non confondersi con i segni quando si somma o sottrae! La somma preserva i segni, il sottrarre cambia i segni della seconda equazione!
-2y = 8 \implies y=-4
Buttiamo questo -4 al posto della y ad esempio della prima equazione (scegliete voi, è la stessa cosa).
-3x +2\cdotp -4 = 1
-3x -8 = 1
Ossia:
-3x = 9 \implies x=-3
Esercizio 11. \begin{cases} -x +2y = 5 \\ x-2y = 10 \end{cases}
Qui sia il termine con la x che quello con la y sono opposti, di fatti uscirà una cosa particolare dopo. Di conseguenza sommiamo membro a membro:
0x +0y = 15
Per qualsiasi valore di x e y, essendo che viene moltiplicato per 0 darà 0. Di conseguenza il membro di sinistra farà sempre 0, e non potrà mai essere uguale a 15. Avremo sempre:
0 = 15
Che ovviamente non è mai verificata, quindi è impossibile!
E’ un po’ il caso analogo di avere 0x=0 per la quale si ha impossibile.
Di conseguenza anche il sistema avrà lo stesso risultato di “impossibile“.
Esercizio 12. \begin{cases} \frac{1}{3}x -2y = \frac{1}{6} \\ -2x +8y = 3 \end{cases}
Qui non c’è nulla di uguale: come fare? In realtà possiamo fare un primo ulteriore passaggio, cioè andiamo a moltiplicare tutta la prima equazione per 4, in questo modo la y raggiungerà il valore di -8y, che quindi sarà l’opposto di 8y nella seconda equazione.
\begin{cases} \frac{4}{3}x -8y = \frac{4}{6} \\ -2x +8y = 3 \end{cases}
Grazie a questo primo passaggio, adesso abbiamo dei termini opposti, e possiamo applicare il metodo di riduzione, sommando membro a membro. Otteniamo l’equazione:
\frac{4}{3}x-2x = \frac{4}{6} +3
Facciamo due minimi comuni multipli (uno a sinistra ed uno a destra):
\frac{4x-6x}{3} = \frac{4+18}{6}
-\frac{2}{3}x = \frac{22}{6}
E cioè:
-\frac{2}{3}x = \frac{11}{3} \implies x= - \frac{11}{2}
Mettiamo questo valore nella seconda equazione (la più semplice), ed otteniamo anche la y:
-2\cdotp (- \frac{11}{2}) +8y = 3
\frac{22}{2} +8y = 3
Isoliamo la y a sinistra:
8y = 3 - 11
8y = -8 \implies y=-1
Ed ora vi è l’ultimo metodo, molto utile per altro!
Sistemi di equazioni col Metodo di Cramer
Per spiegazione ed esercizi sull’utilissimo Metodo di Cramer clicca qui!
In questa pagina abbiamo visto come risolvere un sistema di equazioni con esercizi svolti!
Trovate altri centinaia di esercizi sia di matematica che di geometria analitica e geometria! Continuate a studiare sul nostro sito!
di
Cramer
