Numeri complessi: 20 ESERCIZI SVOLTI
Numeri complessi: 20 ESERCIZI SVOLTI! In questa pagina tratteremo esercizi svolti di numeri complessi, dalle basi fino alle forme esponenziali. Basterà dunque una giornata su questa pagina per prepararsi alla verifica in classe! Prendete carta e penna ed iniziamo!
Indice
- Formulario
- Somma di numeri complessi
- Moltiplicazione tra numeri complessi
- Divisione tra numeri complessi
- Potenze di numeri complessi
- Esercizi sui numeri complessi
- Numeri complessi in forma esponenziale
Prima di iniziare, facciamo un riassunto di tutte le formule che useremo!
Formulario numeri complessi

Iniziamo subito a vedere esercizi svolti numeri complessi: partiamo da una operazione semplice, come si fa la somma di numeri complessi.
Somma di numeri complessi
Esercizio 1. (-9-i) + (2+i) - (-5+2i)
Come possiamo vedere vi sono addizioni e sottrazioni di numeri complessi. La regola principale per la somma di numeri complessi è: si somma parte reale e parte immaginaria separatamente.
Quindi sciogliamo le parentesi, e poi mettiamo la parte reale ad esempio a sinistra, e poi la parte immaginaria (ossia i numeri con la i) a destra:
-9-i + 2+i +5-2i = -9+2 -i+i-2i
E poi sommiamo separatamente parte reale e parte immaginaria. Otteniamo:
-7 -2i
E questo è il risultato finale, cioè il numero complesso finale!
Esercizio 2. \frac{3}{4}i + (2-\frac{1}{3}i)
Così come prima, sciogliamo la parentesi, e poi portiamo separatamente parte reale e parte immaginaria:
\frac{3}{4}i + 2-\frac{1}{3}i = 2 - \frac{1}{3}i + \frac{3}{4}i
La parte reale è 2, ora facciamo il minimo comune multiplo solamente per la parte immaginaria (cioè gli ultimi due numeri):
2+ \frac{-4i + 9i}{12} = 2+ \frac{5}{12}i
E l’esercizio è concluso, abbiamo ottenuto un nuovo numero complesso.
La somma di numeri complessi come vedete non presenta particolari difficoltà. Passiamo avanti andando a vedere come esercizi svolti sulla moltiplicazione di numeri complessi!
Moltiplicazione tra numeri complessi
Esercizio 3. (2-5i)(1+i)
La moltiplicazione fra numeri complessi avviene proprio come un normale prodotto fra polinomi. Quindi andiamo a moltiplicare termine per termine, facendo tutte le combinazioni. Otteniamo:
(2-5i)(1+i)= 2 +2i -5i -5i \cdotp i
Qui, nelle moltiplicazioni è importante ricordare la definizione di unità complessa i:
i= \sqrt{-1} \implies i\cdotp i = i^2 = (\sqrt{-1})^2= -1
E quindi otteniamo:
2 +2i -5i -5 \cdotp (-1) = 2 -3i +5 = 7 -3i
Come sempre, per ordine, andiamo alla fine a sommare le parti reali e immaginarie, e le andiamo a ordinare mettendo la parte reale a sinistra, e quella immaginaria a destra.
Esercizio 4. (2i+7)(2i-7)
Qui non c’è bisogno di fare la moltiplicazione termine per termine, perché notiamo subito che figura una formula molto utile e comodissima (che vi fa risparmiare tanti conti), cioè la formula di differenza di quadrati.
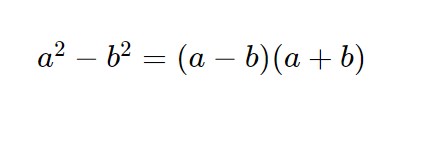
Di conseguenza, seguendo la formula al contrario otteniamo:
(2i+7)(2i-7) = (2i)^2 - 7^2 = 4i^2 - 49 = -4-49 = -53
Con questa moltiplicazione in particolare, il risultato è un numero reale. Questo può capitare tante volte: cioè il risultato non deve essere per forza un altro numero complesso, ma anche contenere solo parte immaginaria o solo parte reale (come in questo caso)!
Conclusa questa parentesi sulla moltiplicazione fra numeri complessi, ne apriamo una sulla divisione fra numeri complessi, un pochetto più fastidiosa.
Divisione tra numeri complessi

Esercizio 5. \frac{3+4i}{2i}
Possiamo identificare due casi diversi che vi possono capitare per la divisione (o frazione) fra due numeri complessi: quando al denominatore c’è solo la parte immaginaria e quando c’è tutto un numero complesso.
Per questo esercizio notiamo che al denominatore c’è 2i, ossia solo parte immaginaria. Ciò che andiamo a fare per eliminare la frazione ed avere un numero complesso è moltiplicare e dividere per il denominatore. Quindi in questo caso moltiplichiamo e dividiamo per 2i.
\frac{3+4i}{2i} = \frac{3+4i}{2i} \cdotp \frac{2i}{2i}
Adesso andiamo a fare la moltiplicazione fra numeratore e numeratore, e denominatore e denominatore. Andiamo quindi ad unire le frazioni in una:
\frac{(3+4i)\cdotp 2i}{(2i)^2} = \frac{6i +8i^2 }{4i^2}
Ricordando che:
i=\sqrt{-1} \implies i^2 = -1
Segue che:
\frac{6i +8\cdotp (-1) }{4 \cdotp (-1)} = \frac{6i-8}{-4}
Grazie ad una proprietà delle frazioni, a questo punto dividiamo in due termini la frazione:
\frac{6i}{-4} + \frac{-8}{-4} = -\frac{3}{2} i + 2
Ed abbiamo così ottenuto un numero complesso nella sua forma base: parte reale + parte immaginaria!
Esercizio 6. \frac{2-i}{2+3i}
Questo è il secondo caso che vi può capitare: cioè che al denominatore c’è un numero complesso completo (reale + immaginaria). Quello che andiamo a fare è sfruttare la formula della differenza di quadrati seguente.
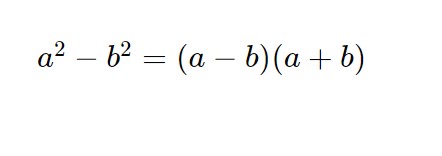
Quindi andiamo a moltiplicare e dividere per il numero complesso del denominatore ma con il segno in mezzo opposto:
\frac{2-i}{2+3i} \cdotp \frac{2-3i}{2-3i} = \frac{(2-i)(2-3i)}{(2+3i)(2-3i)}
Ed ora andiamo a fare la moltiplicazione fra numeri complessi che abbiamo visto prima, e al denominatore applichiamo semplicemente la formula sopra scritta.
\frac{ 4 -6i -2i +3i^2}{2^2-(3i)^2} = \frac{ 4 -6i -2i -3}{4-9i^2}
\frac{ 1 -8i }{4+9 } = \frac{1-8i}{13}
E come prima, per ottenere un numero complesso nella sua forma solita, andiamo a spezzare la frazione in due parti separate, come segue.
\frac{1}{13} - \frac{8}{13}i
L’ultima operazione importante per risolvere esercizi sulle espressioni con numeri complessi, è la potenza di un numero complesso. Vediamole!
Potenze di numeri complessi
Qui le seguenti sono delle formule molto comode e importanti da ricordare per quanto riguarda le potenze di una unità immaginaria!

Esercizio 7. i^7
Quando abbiamo una unità immaginaria i elevata ad un numero superiore di 4 come si fa? Adesso vediamo come utilizzare l’ultima formula sopra scritta.
In pratica dobbiamo prendere l’esponente (7) e dobbiamo dividerlo per 4.
A noi interessa solo del resto: prendiamo il resto (3) e questo sarà il nuovo esponente dell’unità immaginaria!
i^7 = i^3
A questo punto possiamo vedere in tabella sopra, e quindi ottenere il risultato della potenza:
i^3 = -i
Esercizio 8. i^{28}
Come prima, seguiamo lo stesso procedimento: dividiamo l’esponente (28) per 4 e ci segniamo da parte il resto.
Il resto è 0. E di conseguenza:
i^{28} = i^0 = 1
Esercizio 9. (-1+2i)^2
Questo è un quadrato di un binomio complesso, la formula da seguire non cambia ed è sempre la stessa!
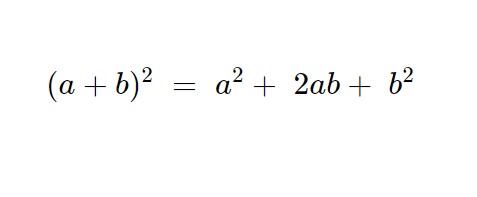
Applicando la formula otteniamo quindi:
(-1+2i)^2 = 1 + (2i)^2 -4i = 1+4i^2 -4i =1 -4-2i = -3 -4i
Come vedete nulla di così diverso da ciò cui siamo abituati!
Vediamo adesso degli esercizi svolti sui numeri complessi, unendo tutte le operazioni. Vediamo come semplificare delle espressioni di numeri complessi!
Esercizi sui numeri complessi
Esercizio 10. (3+2i)(3-2i) + (2-4i)3i - (6+2i)^2
Semplifichiamo questa espressione in un numero complesso. Al primo termine possiamo applicare la formula della differenza di quadrati, poi abbiamo un prodotto fra numeri complessi, e l’ultimo termine è una potenza di un numero complesso.
9 - (2i)^2 + 6i - 12i^2 - (36+4i^2 + 24i) = 9 -4i^2 + 6i - 12i^2 - 36-4i^2 - 24i
Ricordatevi che un meno davanti ad una parentesi cambia tutti i segni dei termini dentro la parentesi. Ricordando che i^2 = -1 scriviamo:
9 +4 + 6i +12 - 36 + 4 - 24i = -7 -18i
L’obiettivo di questi esercizi è sempre lo stesso: semplificare l’espressione che ci dà l’esercizio e ricondurre tutto ad un numero complesso della forma classica.
Esercizio 11. ( \frac{1+2i}{i-1} + \frac{39i}{2+3i} - \frac{19}{2} ) \cdotp 2i + 6i
Partiamo da ciò che c’è dentro la parentesi. Abbiamo due modi di agire: fare subito il minimo comune multiplo oppure fare prima la divisione fra numeri complessi. E’ decisamente più consigliato fare prima la divisione! Per cui moltiplichiamo e dividiamo ogni frazione per il suo denominatore col segno centrale cambiato:
( \frac{1+2i}{i-1} \cdotp \frac{i+1}{i+1} + \frac{39i}{2+3i} \cdotp \frac{2-3i}{2-3i} - \frac{19}{2} ) \cdotp 2i + 6i
( \frac{ (1+2i)(i+1) }{i^2 -1} + \frac{39i(2-3i) }{4-9i^2} - \frac{19}{2} ) \cdotp 2i + 6i
Quando ci sono così tanti calcoli è facile sbagliare, meglio fare una cosa alla volta con calma! Facciamo la moltiplicazione fra le parentesi e semplifichiamo ulteriormente il denominatore ricordando che i^2 =-1 !
( \frac{ i+1+2i^2 +2i}{-2} + \frac{39i(2-3i) }{13} - \frac{19}{2} ) \cdotp 2i + 6i
Inoltre semplifichiamo il 39 col 13:
( -\frac{ 3i-1 }{2} + 3i(2-3i) - \frac{19}{2} ) \cdotp 2i + 6i
( -\frac{ 3i-1 }{2} + 6i - 9i^2 - \frac{19}{2} ) \cdotp 2i + 6i
Come potete vedere, facendo così non serve nemmeno fare il minimo comune multiplo! Questo metodo è quindi molto più comodo, andiamo adesso a scrivere:
( -\frac{ 3i-1 }{2} + 6i +9 - \frac{19}{2} ) \cdotp 2i + 6i
Ora ci conviene sicuramente moltiplicare la parentesi per 2i, non serve nemmeno spezzare la prima frazione, perché tanto il denominatore si semplifica!
-(3i-1)i + 12i^2 +18i - 19i + 6i
3 +i - 12 +18i - 19i + 6i = -9 +6i
Esercizio 12. \frac{3+i}{2-i} - \frac{i-2}{3-i} + (i-1)(i+2) -i
Per le prime due frazioni, effettuiamo la divisione fra numeri complessi, dove quindi moltiplichiamo e dividiamo per i denominatori col segno in mezzo cambiato. Poi svolgiamo la moltiplicazione fra numeri complessi fra quelle due parentesi.
\frac{3+i}{2-i} \cdotp \frac{2+i}{2+i} - \frac{i-2}{3-i} \cdotp \frac{3+i}{3+i} + (i^2 +2i -i -2) -i
Ricordatevi di stare attenti che è facilissimo sbagliare anche un solo segno! Ogni tanto fermatevi, respirate, e ricontrollate tutto!
\frac{(3+i)(2+i) }{4-i^2} - \frac{(i-2)(3+i) }{9-i^2 } -1 +2i -i -2 -i
Effettuiamo prima di tutto la moltiplicazione fra le parentesi presente ai due numeratori, inoltre sommiamo già giusto gli ultimi termini!
\frac{ 6+3i+2i+i^2 }{5} - \frac{ 3i+i^2 - 6 -2i }{10 } -3
Che sarebbe:
\frac{ 5+5i }{5} - \frac{ i - 7 }{10 } -3
Spezziamo le frazioni, e così otteniamo somme semplici e l’esercizio volgerà al termine!
1+i - \frac{1}{10}i + \frac{7}{10 } -3
Sommiamo separatamente le parti reali e immaginarie, quindi facciamo due mcm diversi:
\frac{10+7-30}{10} - \frac{10-1}{10}i = -\frac{13}{10} + \frac{9}{10}i
Esercizio 13. \frac{ (2i^{28} - i^{45} )^2 }{2i^{41} }
Prima di iniziare a toccare mano a fare moltiplicazioni ed altro, dobbiamo innanzitutto come primissima cosa risolvere quelle potenze di unità immaginarie! Facciamo quindi le 3 divisioni. Partiamo con il primo esponente 28.
Abbiamo quindi come resto 0, per cui:
i^{28} = i^0 = 1
Facciamo lo stesso per le altre due potenze. Non vi lasciamo il disegno delle frazioni, scriviamo direttamente i risultati.
i^{45} = i^1 = i
i^{41}= i^1 = i
Piuttosto che fare ogni volta una divisione che comunque fa perdere tempo ed è noiosa, vi insegno un trucchetto per fare prima! In pratica partite da 4 e dite la tabellina del 4 fino a che non vi avvicinate al numero dell’esponente. Quando vi siete avvicinati contate quanto ci vuole per arrivarci esattamente. Per esempio, se l’esponente è 41 allora contante così:
4-8-12-...-40
Ora che vi siete avvicinati più che potete, quanto ci vuole per arrivare a 41? Beh 1! E quindi il resto è proprio 1!
Ritorniamo all’esercizio, sostituiamo i risultati ottenuti:
\frac{ (2 - i)^2 }{2i } = \frac{4+i^2 - 4i}{2i} = \frac{3-4i}{2i}
Ora l’esercizio è praticamente quasi concluso, andiamo semplicemente ad effettuare la divisione di numeri complessi. Moltiplichiamo e dividiamo quindi per il denominatore 2i:
\frac{3-4i}{2i} = \frac{3-4i}{2i} \cdotp \frac{2i}{2i} = \frac{(3-4i)2i}{4i^2}
Effettuiamo la moltiplicazione al numeratore, e poi…chiaramente andremo a spezzare la frazione!
\frac{6i - 8i^2}{-4} = \frac{6i +8}{-4} = -2 - \frac{3}{2} i
Attenti sempre ai segni! Questi esercizi non sono così complicati, quindi attenzione che potrete aumentare la media: questa è l’occasione davvero perfetta per prendere un discreto voto alla verifica in classe!
Esercizio 14. (1+i)^5 + 4i
Qui bisogna procedere con furbizia ed intelligenza, altrimenti usciranno fuori calcoli infiniti. Scriviamo la potenza come segue, semplicemente sfruttando una delle proprietà delle potenze:
(1+i)^5 + 4i = (1+i)(1+i)^2(1+i)^2 + 4i
Prendiamo il termine (1+i)^2 da parte e calcoliamolo. Se ve lo state chiedendo, abbiamo diviso la potenza in tre termini perché potenze superiori sono difficili da calcolare, mentre un quadrato di un binomio lo sappiamo fare.
(1+i)^2 = 1+i^2 +2i = 1-1 +2i = 2i
Sostituiamo nell’espressione. Come vedete abbiamo ben due quadrati uguali! Quindi:
\implies (1+i)\cdotp 2i \cdotp 2i + 4i = (1+i) \cdotp 4i^2 +4i
\implies -(1+i)4 +4i
E questa è una moltiplicazione super facile da fare rispetto a quella che avevamo prima! L’abbiamo risolta anche con pochissimi passaggi! La furbizia è sempre buon alleato: osservate bene l’espressione o equazione che la professoressa vi dà, in modo da individuare eventuali semplificazioni o altro.
-(1+i)4 +4i = -4-4i +4i = -4
La parte riguardante l’espressione esplicita di numeri complessi ed operazioni di numeri complessi è conclusa! Vediamo adesso altre varianti e sezioni riguardo sempre ai numeri complessi!
Numeri complessi in forma esponenziale
Esercizio 15. z= 2+2i
Troviamo la forma esponenziale di questo numero complesso.
PRIMO PUNTO: calcolare il modulo del numero complesso, utilizzando la formula sopra scritta nella tabella, ossia:
z=a+ib \implies \rho = \sqrt{a^2 + b^2}
Nel nostro caso a=2 mentre b=2, poiché sarebbe il coefficiente dell’unità immaginaria!
Quindi il modulo di z in questo caso sarà:
\rho =\sqrt{2^2 + 2^2} = \sqrt{4+4} = \sqrt{8}
SECONDO PUNTO: trovare l’argomento del numero complesso. In pratica dobbiamo trovare l’angolo \theta che si forma nel piano complesso fra il raggio e l’asse x.
La formula della trigonometria che ci permette di trovare tale angolo deriva dalla formula:
\tg \theta = \frac{b}{a} = \frac{2}{2} = 1
(Senza mettere la i nella formula per ricavare l’angolo mi raccomando)
Questa è una equazione goniometrica elementare, quindi l’angolo lo ricaviamo semplicemente dalla calcolatrice: premiamo shift, poi tangente, poi inseriamo 1 ed infine ci darà un angolo. Nel nostro caso ci darà:
\implies \theta = 45° = \frac{\pi}{4}
Ora in realtà a volte ci sarebbe bisogno di aggiungere un \pi a tale angolo. Per vedere se l’angolo che ci dà la calcolatrice va bene, dobbiamo controllare la figura sotto (disegno del punto z in un piano complesso). Come vedete il punto sta nel primo quadrante, e l’angolo di \frac{\pi}{4} sta anch’esso nel primo quadrante, sono concordi e quindi va bene!
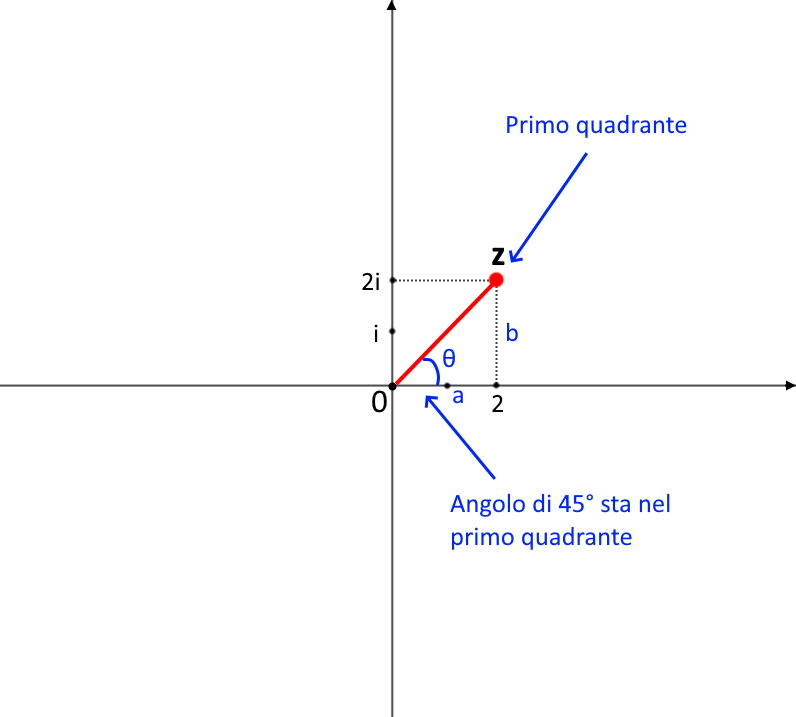
Il numero complesso quindi si scriverà nella forma esponenziale:
z=\rho e^{i \theta } = \sqrt{8} e^ {i \frac{\pi}{4} }
Se poi la volessimo anche nella forma trigonometrica, basta semplicemente applicare la formula sempre scritta in tabella.
E quindi:
z = \sqrt{8} e^ {i \frac{\pi}{4} } \implies z = \sqrt{8} (\cos \frac{\pi}{4} + i \sin \frac{\pi}{4} )
Esercizio 16. z = -2i
PRIMO PUNTO: modulo. Notiamo fin da subito che non ha la parte reale, quindi i due coefficienti sono a=0, b=-2. Detto questo calcoliamo pure il modulo usando sempre quella formula:
\rho = \sqrt{a^2 + b^2} = \sqrt{(-2)^2}=2
SECONDO PUNTO: argomento del numero complesso, ossia l’angolo che forma nel piano complesso. Usiamo sempre la solita formula detta prima anche:
\tg \theta = \frac{b}{a} = \frac{-2}{0} = - \infin
In questo caso la formula non ci dà l’informazione che noi vogliamo. Questo perché se vi ricordate, la tangente non è definita nei punti \frac{\pi}{2} e \frac{3}{2} \pi . Quando abbiamo un caso del genere, facciamo direttamente il disegno del piano complesso e ricaviamo l’angolo manualmente. In realtà si vede ad occhio come vedete.
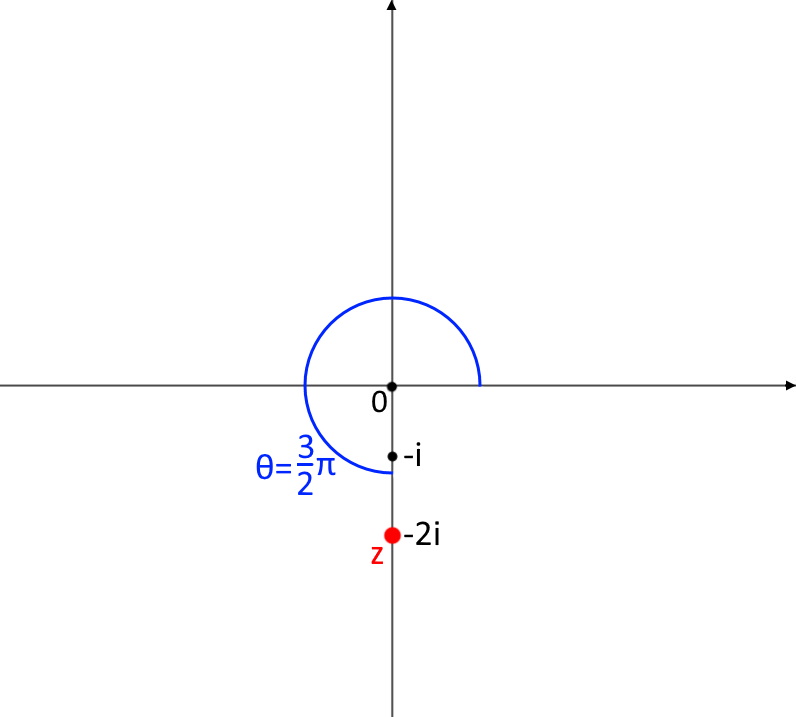
L’angolo/ argomento è quindi \frac{3}{2} \pi .
Il numero complesso di questo esercizio in forma esponenziale si scriverà dunque come:
z= 2 \; e^{i \frac{3}{2} \pi }
Che in forma trigonometrica è poi:
z = 2 (\cos \frac{3}{2} \pi + i \sin \frac{3}{2} \pi )
Esercizio 17. z = - \sqrt{3} -i
PRIMO PUNTO: modulo. Calcoliamo come sempre prima di tutto il modulo (cioè alla fine sarebbe la lunghezza del raggio) del numero complesso. In questo esercizio come vedete a=- \sqrt{3} , e b=-1.
\rho = \sqrt{a^2 + b^2} = \sqrt{(- \sqrt{3})^2 + (-1)^2}=\sqrt{3+1}=2
SECONDO PUNTO: argomento. Utilizziamo sempre la solita formula trigonometrica della tangente, dove però qui c’è da STARE ATTENTI ed ora vedremo perché!
\tg \theta = \frac{b}{a} = \frac{-1}{- \sqrt{3}} = \frac{1}{\sqrt{3} }
Razionalizzando:
\tg \theta = \frac{\sqrt{3}}{3} \implies \theta =\frac{\pi}{6}
QUESTO PERO’ NON E’ L’ANGOLO DA USARE! Come detto due esercizi fa, a volte è necessario aggiungere un \pi, e questo lo possiamo dedurre disegnando il piano complesso.
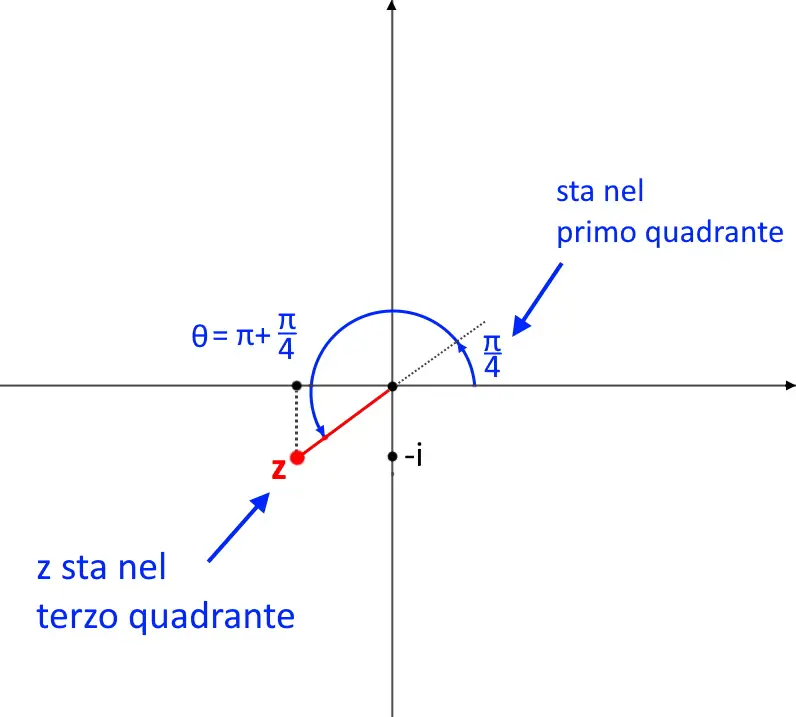
Come vedete l’angolo di \frac{\pi}{6} = 30° sta nel primo quadrante, mentre il raggio corrispondente al numero complesso z sta nel terzo quadrante. Quando c’è questa non corrispondenza allora dobbiamo aggiungere un \pi.
\implies \theta = \frac{\pi}{6} + \pi = \frac{7}{6} \pi
Ora sì che possiamo scrivere il numero complesso nella sua forma esponenziale!
z= 2 \; e^{i \frac{7}{6} \pi }
E la sua forma trigonometrica sarà:
z = 2 (\cos\frac{7}{6} \pi + i \sin \frac{7}{6} \pi )
In questa pagina abbiamo trattato esercizi svolti sui numeri complessi di ogni tipo! Sul nostro sito trovate altre centinaia di pagine come questa con tantissimi esercizi svolti e spiegati mano mano, sia di matematica che altro ancora!
Per approfondire:
https://it.wikipedia.org/wiki/Numero_complesso
Numeri complessi esercizi svolti
goniometriche
esercizi