Funzione suriettiva, iniettiva e biiettiva: definizioni ed esempi
In questa pagina capiremo cosa sono è una funzione suriettiva, iniettiva e biiettiva. Argomento sottovalutato ma super delicato, e spesso descritto in maniera superficiale sui libri. Noi cercheremo di spiegarvi passo dopo passo e con tanti esempi cosa sono le funzioni suriettive, iniettive e biiettive, e perché sono importanti. Iniziamo subito!
Indice
Prima di iniziare, ripetiamo al volo cosa è una funzione, cui già ne abbiamo parlato abbondantemente nella pagina dedicata.
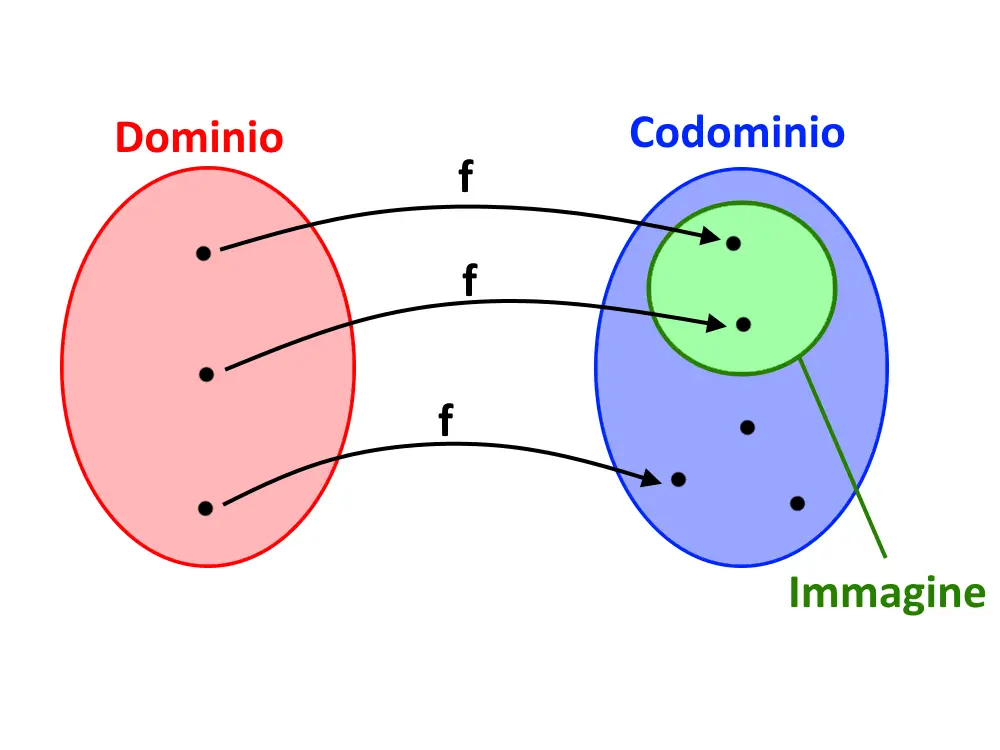
Una funzione f: A \to B associa ad ogni elemento A un solo elemento di B (cioè da ogni oggetto di A parte una sola freccia). Avevamo detto che A, insieme di partenza, era detto dominio. L’insieme di arrivo B l’avevamo chiamato codominio. Poi gli oggetti di B che venivano associati rappresentano un insieme chiamato immagine della funzione. (In molti libri confondono codominio con l’immagine, state attenti, sbagliano anche loro)
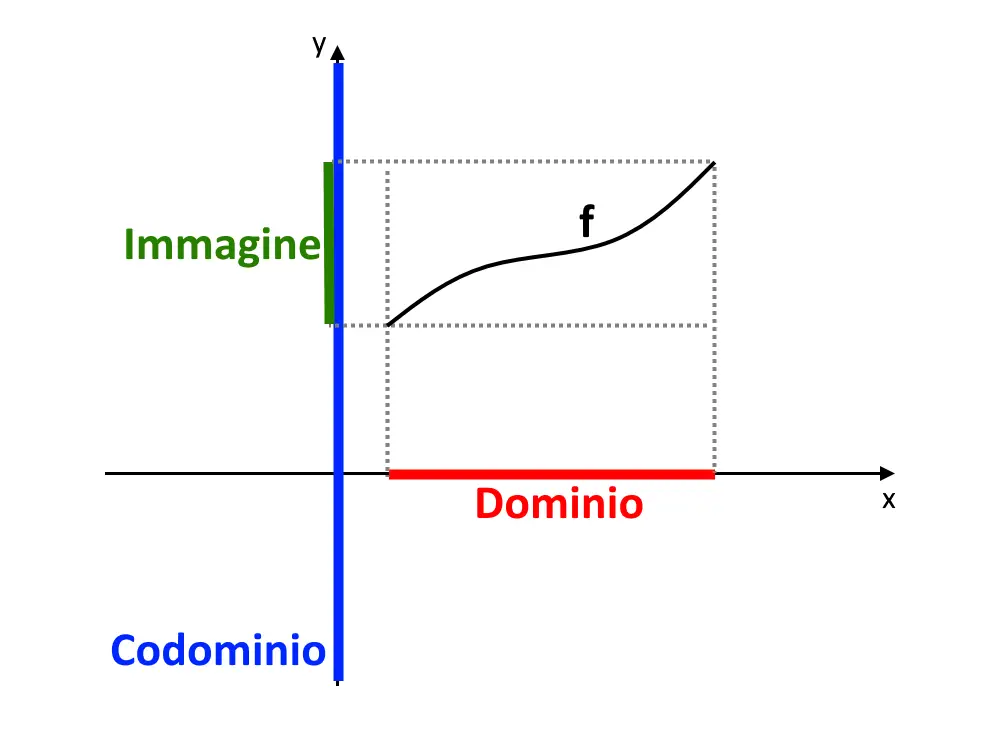
Abbiamo notato che al Liceo si studiano solo le funzioni reali, di conseguenza i due insiemi A e B sono dei numeri reali. Mettiamo il dominio sull’asse x di un piano cartesiano, ed il codominio sull’asse y. Il codominio ce lo deve dare il libro, non possiamo trovarlo noi: esso può essere tutto l’asse y o una parte (ripetiamo che ce lo dà il libro o l’esercizio). L’immagine invece possiamo trovarla noi, ed è quella parte dell’asse y cui vi corrispondono punti della funzione. La funzione f è il grafico.
Queste funzioni, cui vi invito a cliccarci prima di iniziare, si dividono in tre grandi categorie: suriettive, iniettive e biiettive. Ognuna di questa ha delle caratteristiche diverse. La più importante è quella biiettiva, perché se una funzione è biiettiva allora può anche essere invertibile, quindi ha diretto riscontro anche negli esercizi.
In ogni sezione di questa pagina partiremo dalle definizioni di ognuna e passeremo a grafici ed esempi pratici! Iniziamo!
Funzione suriettiva
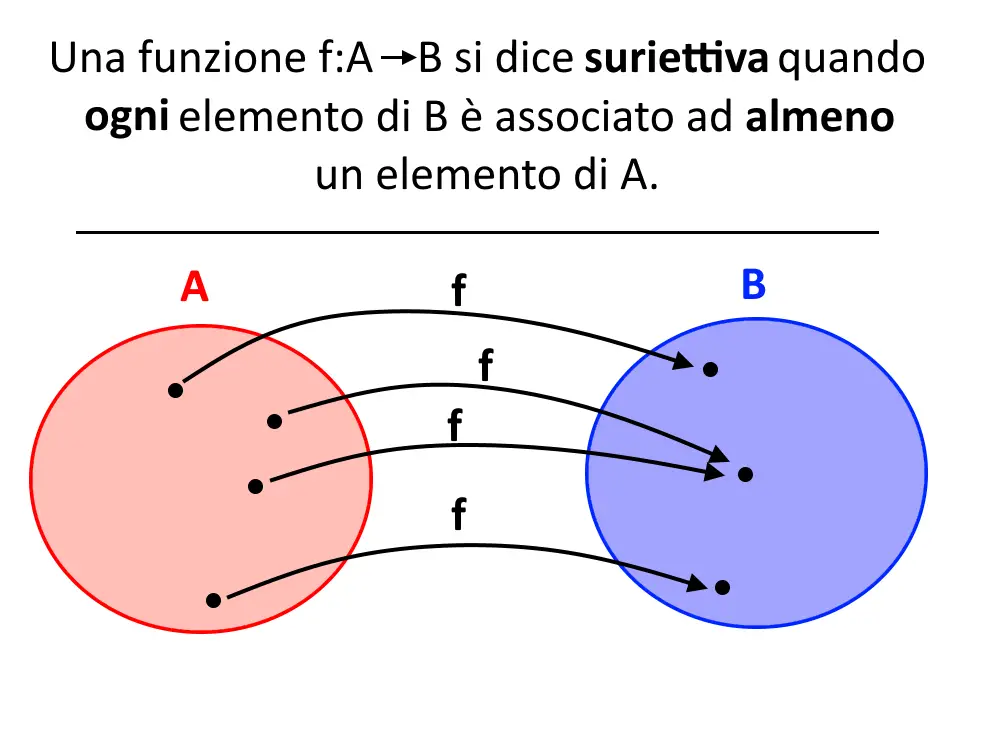
Ok, ma quindi in pratica cosa vuol dire? Spieghiamo una cosa per volta con calma. Nella pagina delle funzioni, avevamo detto che B era il codominio. Il codominio è un insieme che ce lo deve dare il libro. Di fatti il codominio può essere tutto l’asse y, oppure una parte. Poi c’è l’immagine, che sono un insieme di punti cui corrisponde appunto l’immagine della funzione. L’immagine invece non è a scelta, ma deve corrispondere la funzione.
Detto questo rispondiamo alla domanda. Nella definizione sta scritto che ad ogni elemento di B arriva almeno una freccia: questo significa che tutti gli elementi di B, ossia del codominio, sono occupati. Ma gli oggetti di B associati ad una freccia fanno parte dell’immagine: di conseguenza codominio ed immagine coincidono nelle funzioni suriettive!
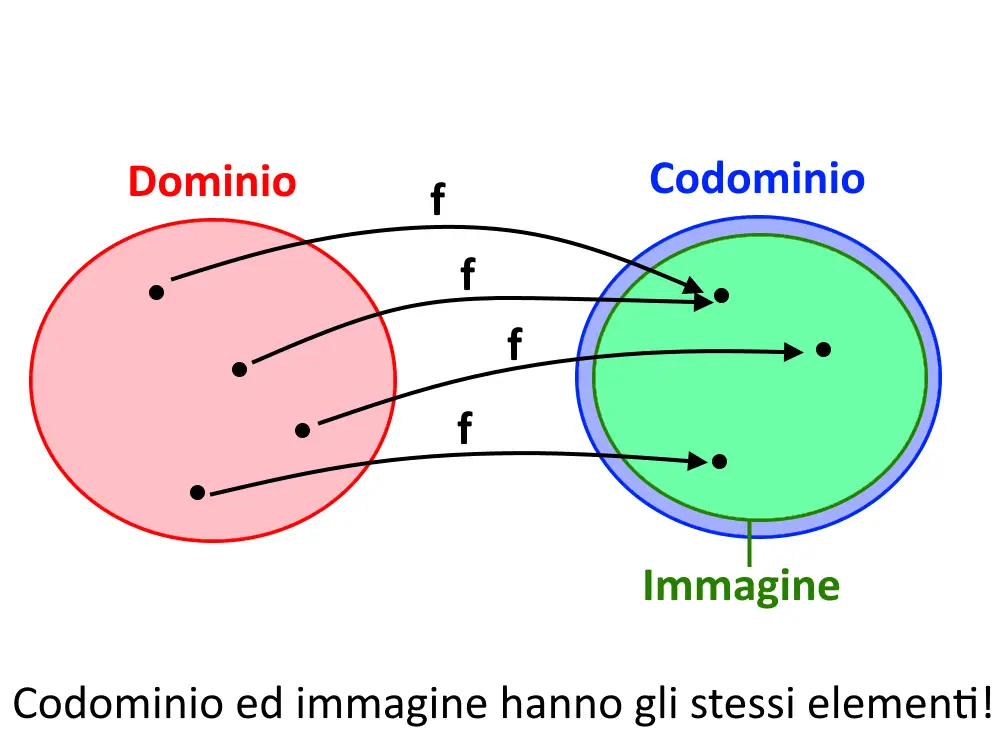
La funzione suriettiva si rappresenta, in degli assi cartesiani, in qualcosa del genere dove vi mostriamo anche i vari insiemi.
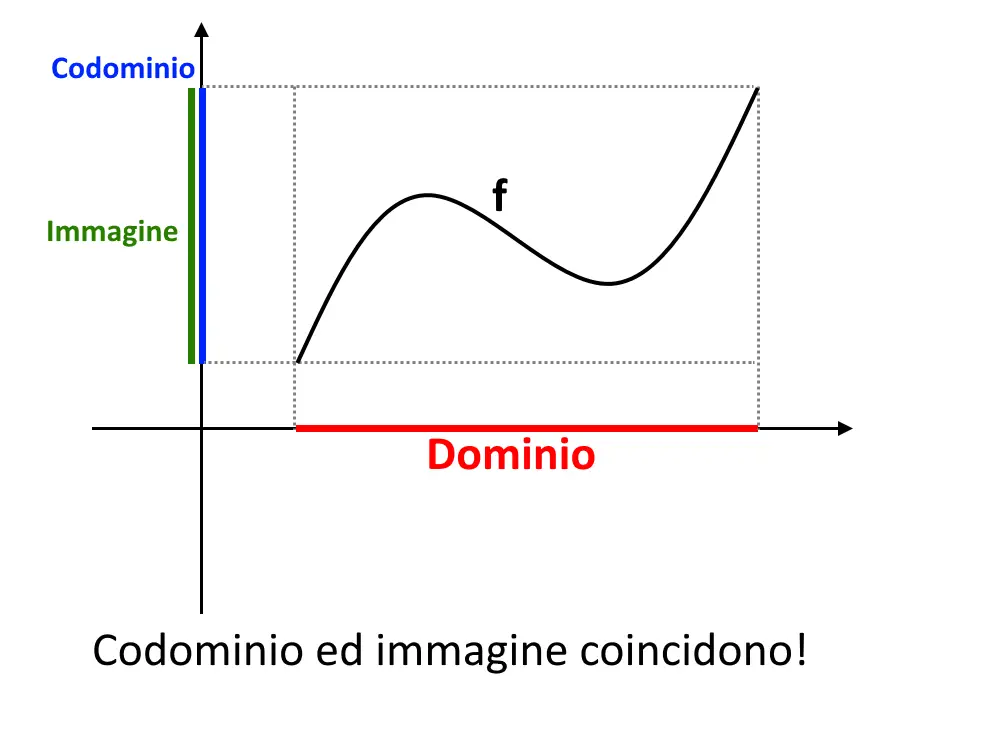
Notate come codominio coincide con l’immagine. In questo preciso caso immagine e codominio sono insiemi uguali. Vediamo altri esempi! Sottolineiamo che questi seguenti esempi potrebbero essere di un livello un po’ più alto.
Funzioni suriettive: grafici ed esempi
Esempio 1. Consideriamo la funzione f: \Reals \to \Reals dove f: x \in dom(f) \longmapsto y=x
Solitamente il libro vi dirà questo. La prima notazione ci dice gli insiemi (quindi A= \Reals , \; B= \Reals ): la traccia ci sta dicendo che tutto l’asse reale x è il dominio, e tutto l’asse y è il codominio. La funzione in sé ci viene esplicitata con la seconda notazione, e rappresenta il grafico. Da questa possiamo ricavare l’immagine.
Vi mostriamo il grafico di questa funzione f(x)=x.
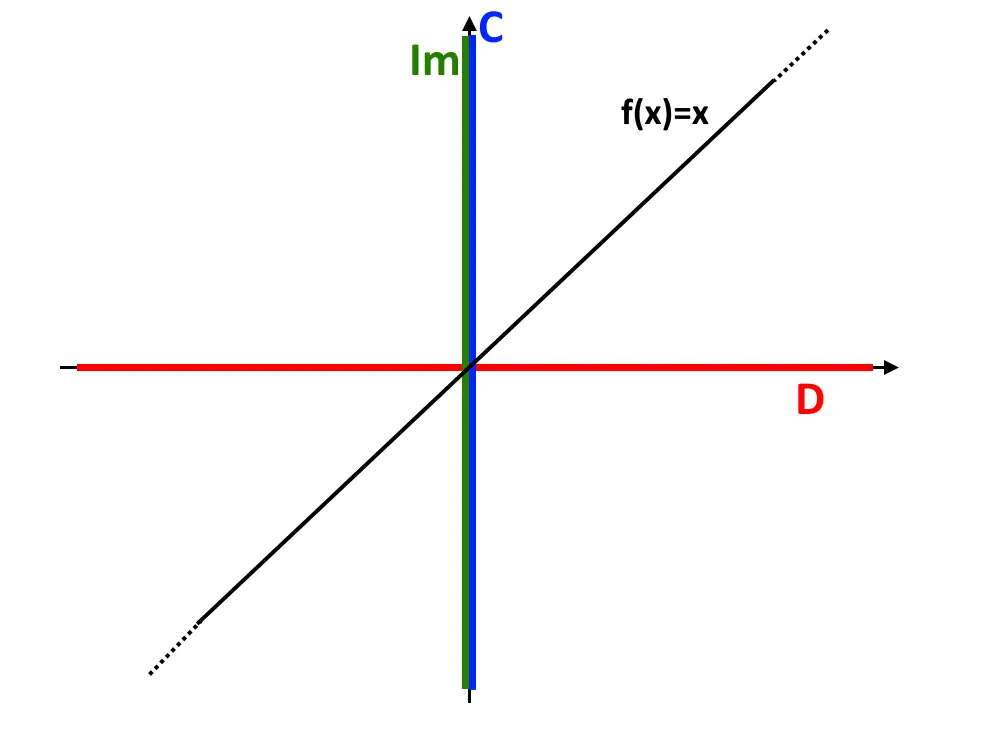
Come possiamo vedere codominio ed immagine coincidono, quindi la funzione è suriettiva!
Esempio 2. Consideriamo la funzione f: [0, + \infin [ \to \Reals dove f: x \in dom(f) \longmapsto y=\sqrt{x}
Mettiamo sugli assi dominio e codominio. Poi vi mostriamo il grafico della funzione f(x)= \sqrt{x} . Dopo aver disegnato il grafico della funzione notiamo che l’immagine sta solo nella parte superiore dell’asse y. Quindi codominio ed immagine non sono uguali.
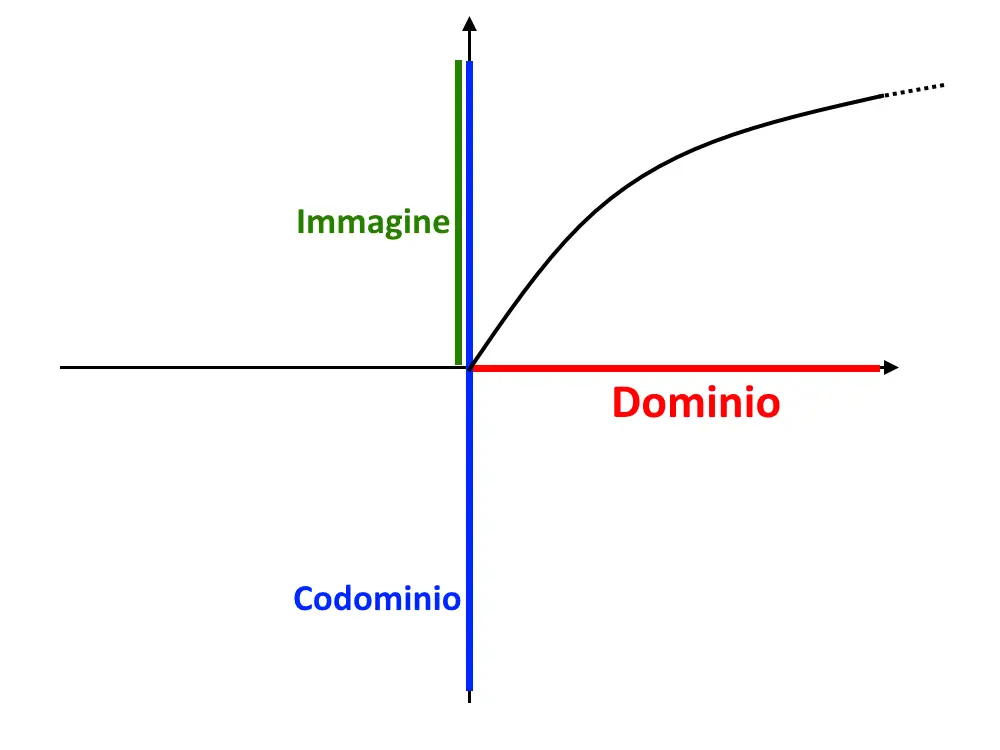
Qua invece codominio ed immagine non coincidono, la funzione non è suriettiva!
Esempio 3. Consideriamo la funzione f: \Reals \to \Reals dove f: x \in dom(f) \longmapsto y=x^3
Anche in questo caso lungo tutta la lunghezza degli assi cartesiani ci piazziamo dominio e codominio. La funzione f(x)=x^3 è precisamente la seguente. Come possiamo notare codominio ed immagine coincidono. Quindi la funzione è suriettiva!
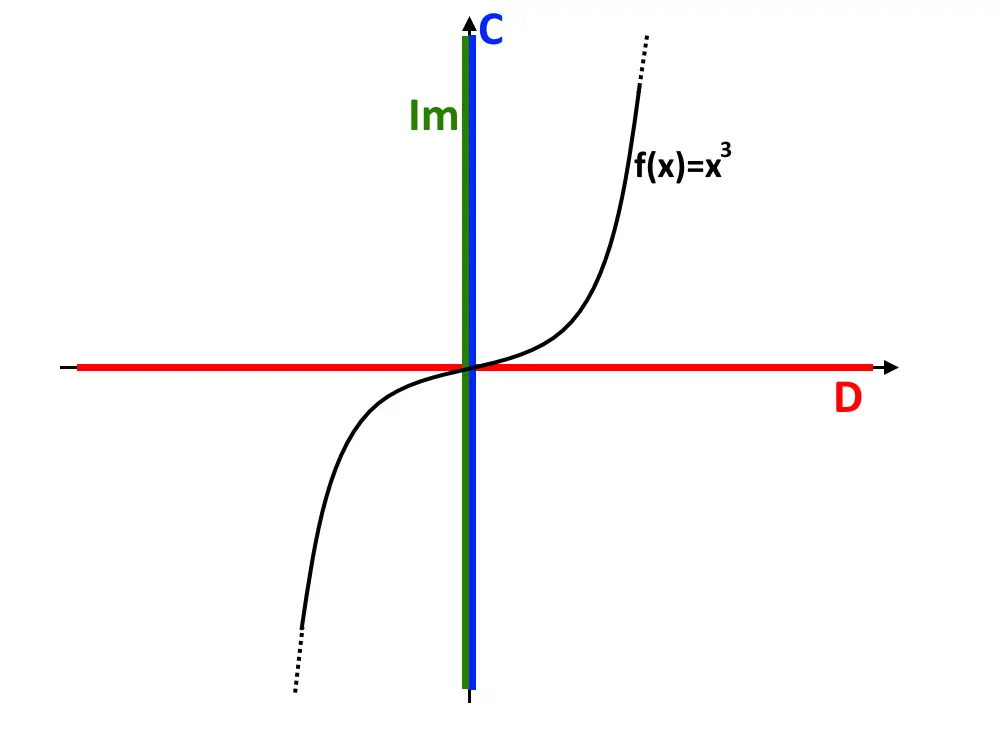
Passiamo adesso a vedere cosa sono e cosa significano le funzioni iniettive!
Funzioni iniettive
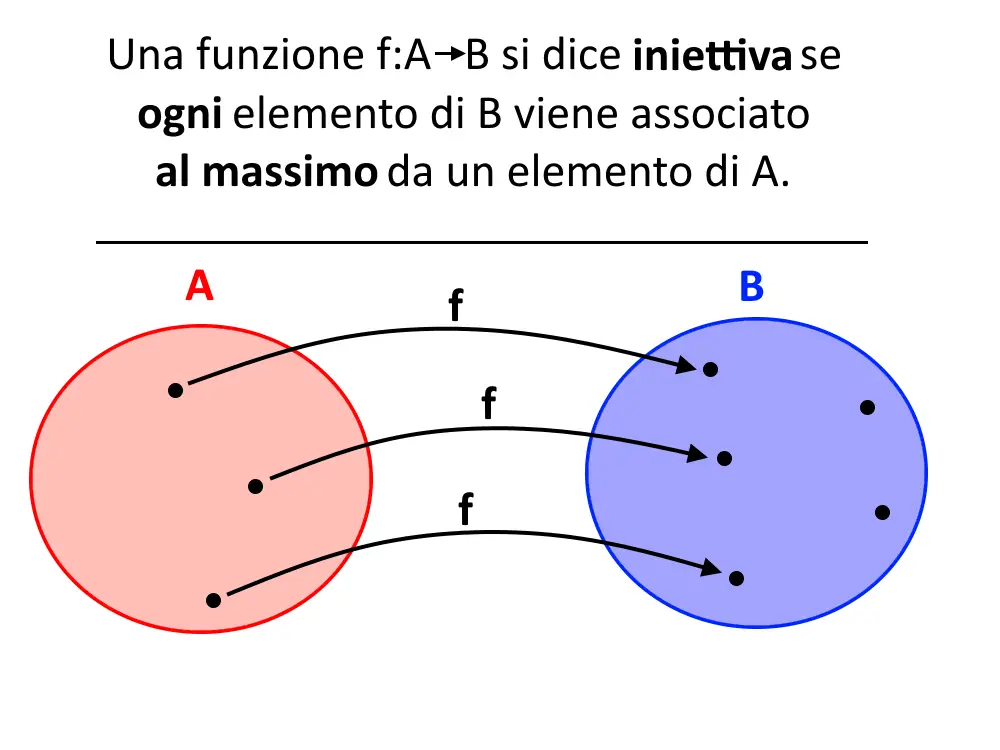
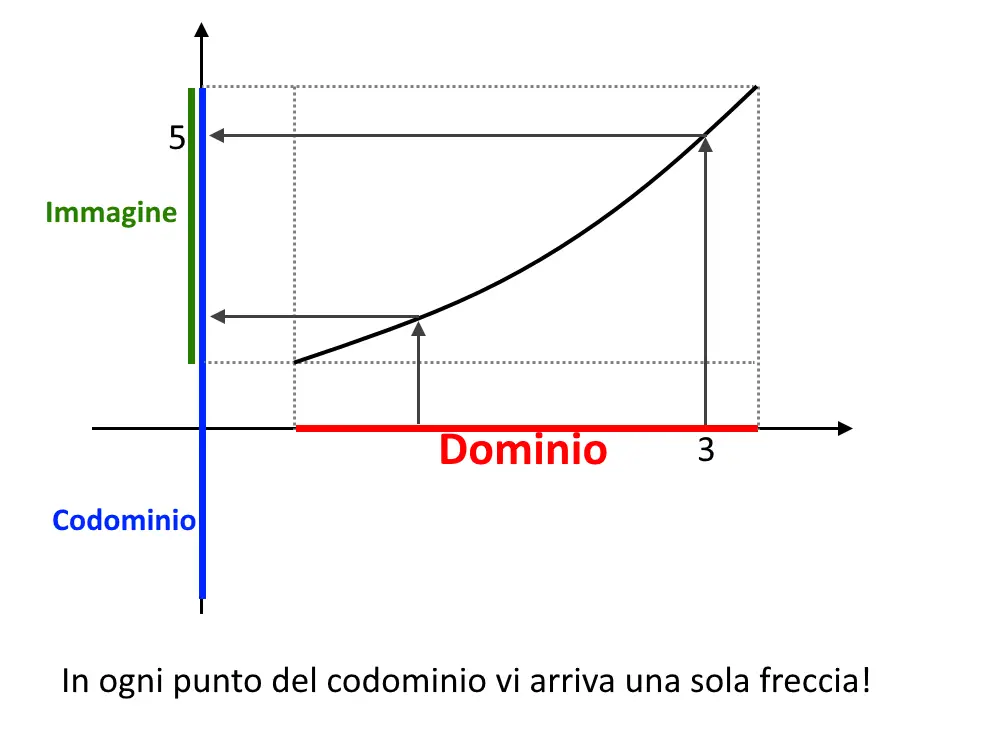
Cosa significa questa definizione? Per ogni oggetto di B arriva massimo una freccia. Facciamo un esempio parlando degli assi cartesiani, che è quello che ci interessa. In pratica ad ogni punto del dominio (insieme A) viene associato un solo punto del codominio (insieme B). Nel seguente esempio, come vedete, ogni punto dell’asse x (nel dominio) corrisponde ad un solo punto dell’asse y (nel codominio). Come vedete, per esempio l’oggetto x=3 in A viene associato il solo oggetto y=5 in B. Nell’oggetto y=5 di B arriva al massimo una freccia.
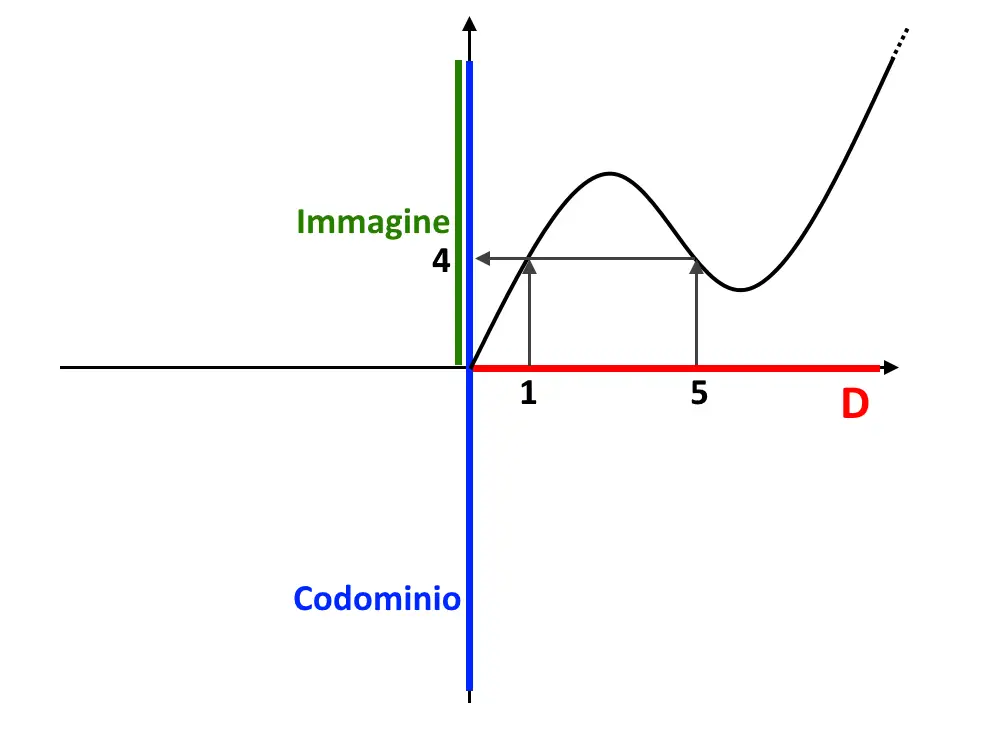
Per capire ancora meglio, consideriamo adesso un diverso esempio seguente dove la funzione non è iniettiva. Notiamo che nell’immagine seguente, a due punti del dominio (insieme A) vengono associati lo stesso punto del codominio (insieme B). Cioè x=1 e x=5 (di A) sono associati allo stesso punto y=4 (di B). Quindi nell’oggetto y=4 di B arrivano due frecce. Quindi tale funzione non è iniettiva!
Vediamo altri esempi e grafici per capire ancora di più cosa è una funzione iniettiva!
Esempi di funzioni iniettive
Esempio 4. Consideriamo la funzione f: \Reals \to \Reals dove f: x \in dom(f) \longmapsto y=x+2
Questa è una funzione iniettiva, perché vedendo il grafico di questa funzione notiamo che ad ogni punto di x nel dominio vi corrisponde un solo punto y nel codominio.
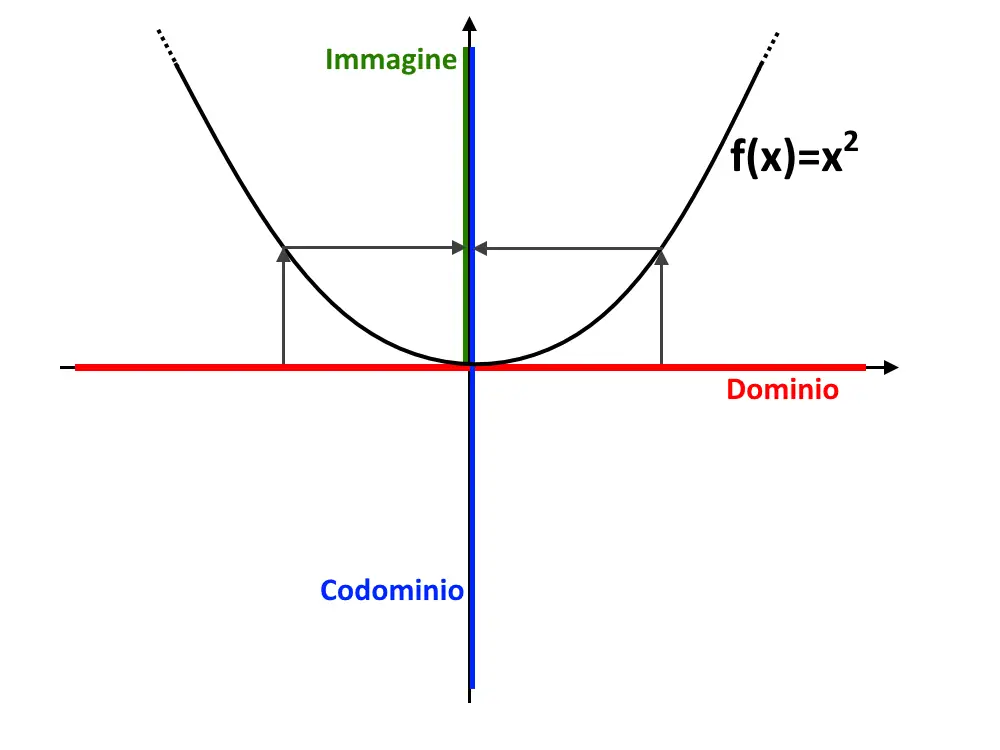
Esempio 5. Consideriamo la funzione f: \Reals \to \Reals dove f: x \in dom(f) \longmapsto y=x^2
Vedendo il grafico, capiamo che questa non è una funzione iniettiva. Se prendiamo per esempio un oggetto qualsiasi di B vi corrispondono due punti diversi (arrivano due frecce).
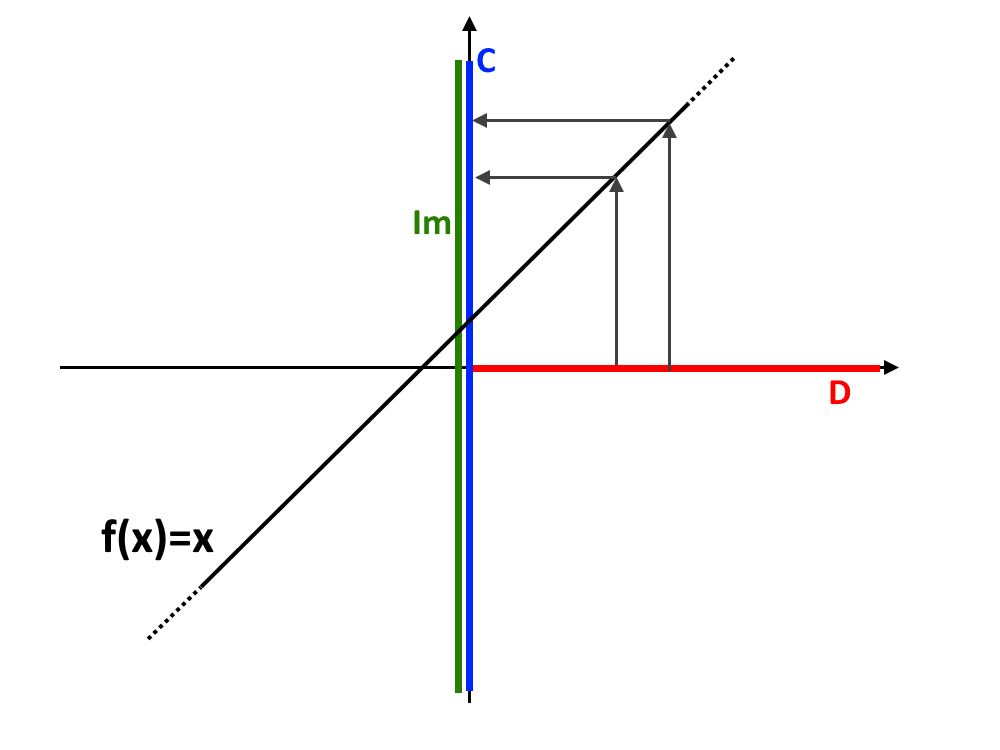
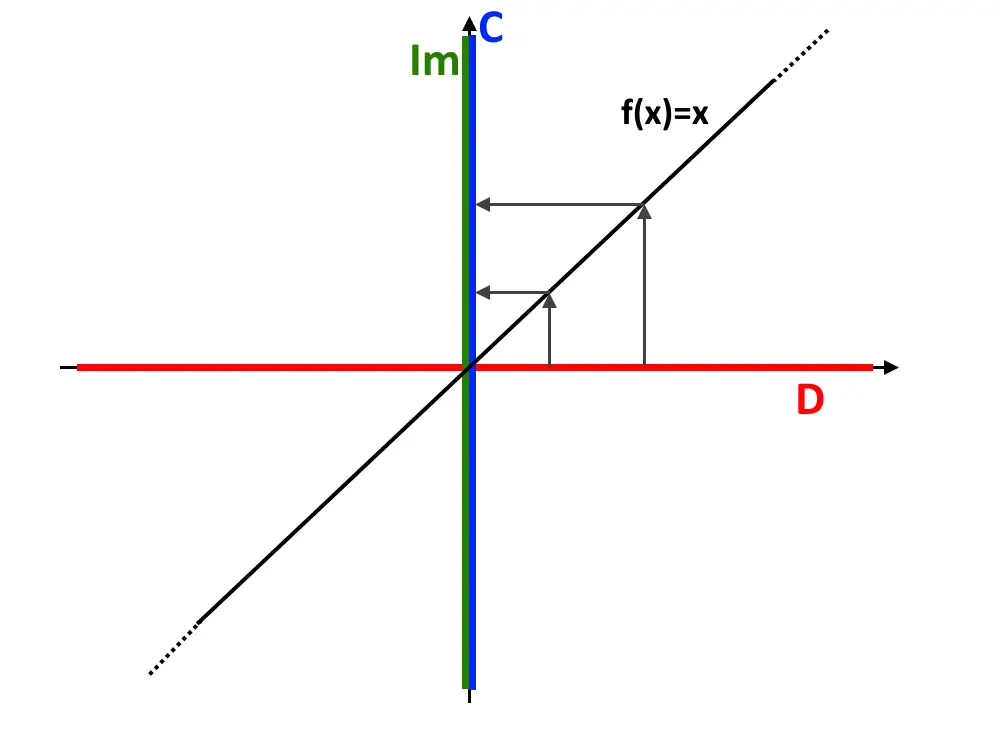
Esempio 6. Consideriamo la funzione f: \Reals \to \Reals dove f: x \in dom(f) \longmapsto y=x
Il grafico di questa funzione l’abbiamo già visto in un esempio precedente. E avevamo detto che questa era suriettiva…beh è anche iniettiva! Se prendiamo un qualsiasi punto sulla y arriva solamente una volta al grafico, cui corrisponde quindi una sola x!
Adesso passiamo all’ultima sezione, quella più importante, che riguarda le funzioni biiettive!
Funzioni biiettive
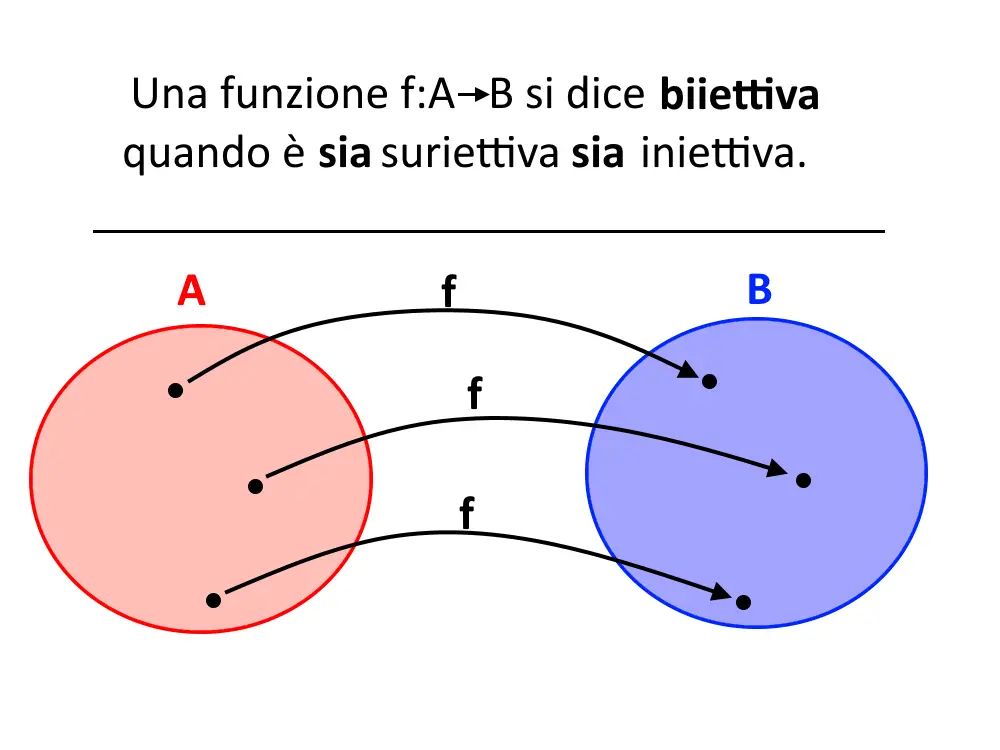
Cosa significa questo? La definizione sta dicendo che ogni elemento di B è occupato (quindi codominio coincide con immagine) ed in più sta dicendo che ad ogni oggetti di B arriva una freccia.
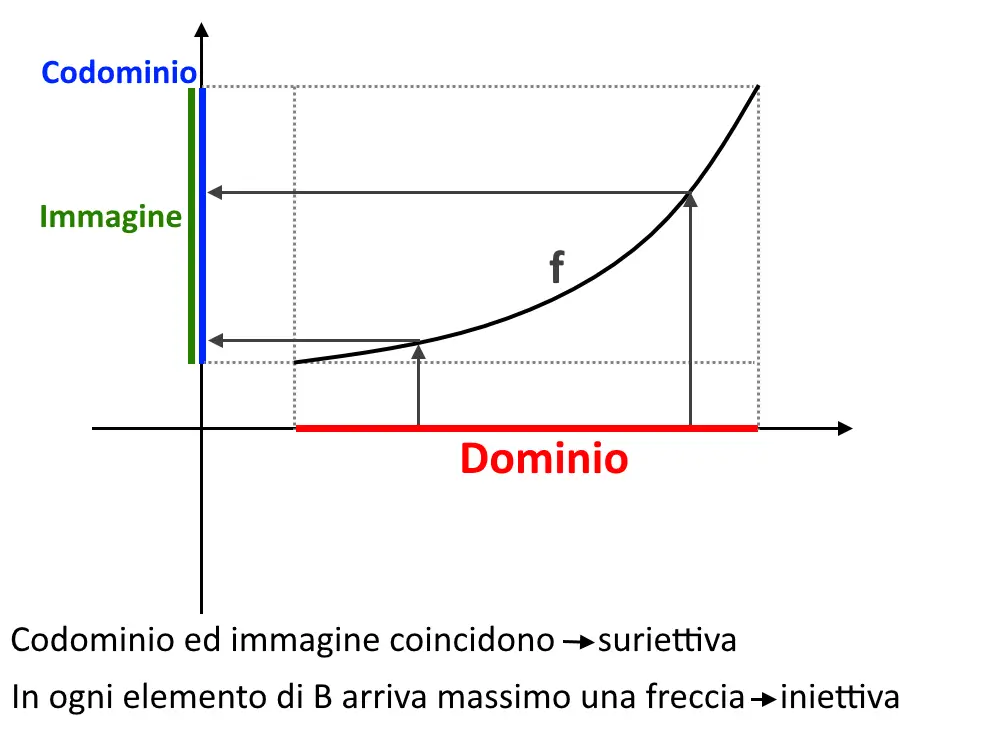
Unendo queste due considerazioni, una funzione biiettiva (o biunivoca) è una funzione che è sia suriettiva che iniettiva! Dalla caratteristica suriettiva prende il fatto che tutti gli oggetti di B sono occupati (e quindi codominio coincide con l’immagine). Poi dalla caratteristica iniettiva prende il fatto che ad ogni oggetto di B arriva al massimo una freccia, ma visto che sono tutti occupati allora prende una sola freccia. Un esempio è la seguente funzione.
Una funzione che possiede questa caratteristica è anche invertibile, ma questo è un altro paio di maniche.
Vediamo degli esempi di grafici di funzioni biiettive!
Funzioni biiettive: esempi
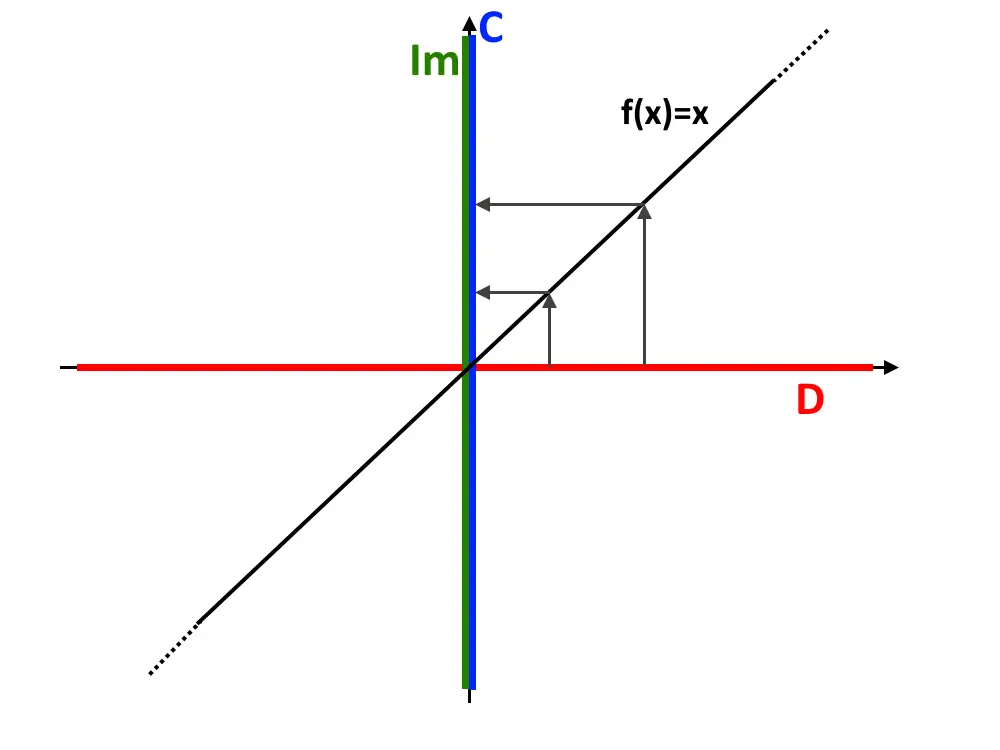
Esempio 7. Consideriamo la funzione f: \Reals \to \Reals dove f: x \in dom(f) \longmapsto y=x
La prima è questa! Negli scorsi esempi abbiamo detto che questa funzione è sia suriettiva che iniettiva, e di conseguenza è biiettiva!
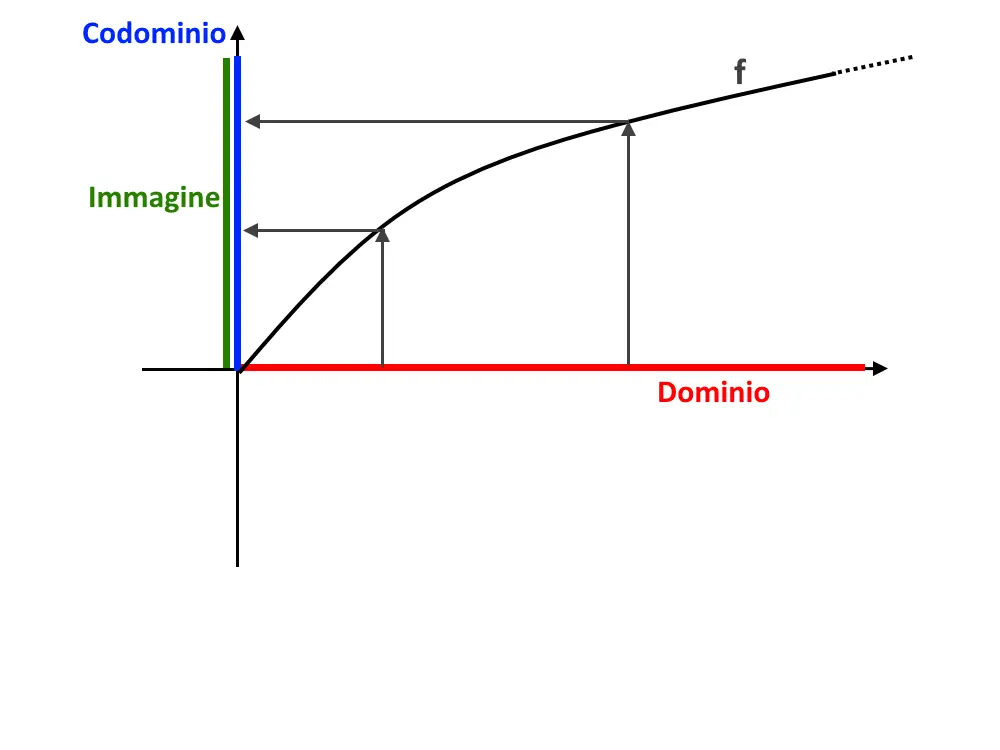
Esempio 8. Consideriamo la funzione f: [0, + \infin [ \to [0, + \infin [ dove f: x \in dom(f) \longmapsto y= \sqrt{x}
Questa è una funzione biiettiva come vedete, perché codominio ed immagine coincidono e poi è anche iniettiva!
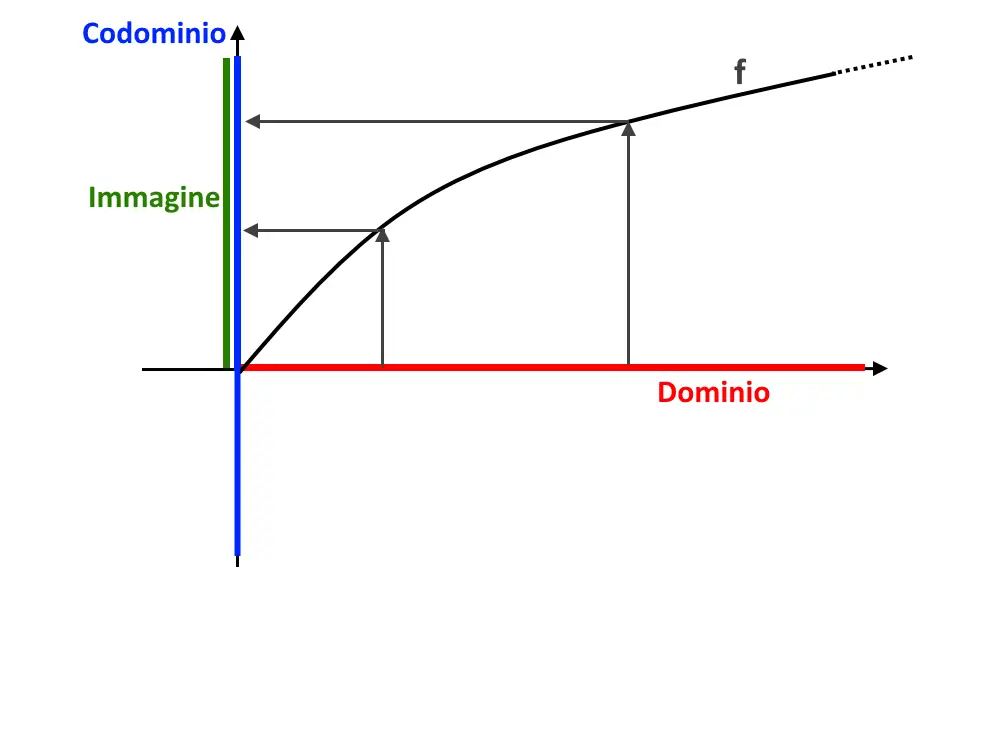
Esempio 9. Consideriamo la funzione f: [0, + \infin [ \to \Reals [ dove f: x \in dom(f) \longmapsto y= \sqrt{x}
Questa è sì la stessa funzione di prima (stesso grafico), ma è su insiemi diversi. Di fatti adesso codominio ed immagine non coincidono, quindi non è più biiettiva.
Concludiamo questa pagina aggiungendo che molto spesso nei libri, per semplificare le cose, fanno sempre coincidere codominio ed immagine. Quindi le funzioni saranno considerate tutte almeno suriettive d’ora in poi.
Abbiamo visto in questa lunga pagina degli argomenti delicati, dove anche all’università si hanno sempre dei dubbi, a causa anche di superficialità nei libri. Se siete interessati ad avere più informazioni riguardo la facoltà di matematica, una delle migliori è l’Università di Pisa. Facoltà non semplice ma molto interessante.
Trovate comunque altre centinaia di argomenti di matematica, geometria analitica e geometria sul nostro sito!
Continuate a supportarci!
teoria
esempi
crescenti
decrescenti