Funzione continua e continuità in un punto
Funzione continua e continuità in un punto: in questa pagina vedremo cosa la definizione e cosa significa che una funzione è continua. Mostreremo degli esempi e dei piccoli esercizi svolti con il loro procedimento.
Indice
- Funzione continua in un punto
- Funzione non continua in un punto
- Esempi di funzioni continue in un punto
- Funzioni continue nel dominio
Iniziamo subito a vedere il significato e la definizione di continuità in un punto!
Funzione continua in un punto
Per capire cosa significa davvero che una funzione è continua in un punto, mostriamo il seguente esempio. Consideriamo una certa funzione f(x). Nel suo dominio, alla componente x_0 vi corrisponde la componente y_0 (detto anche f(x_0)) di un certo punto P.
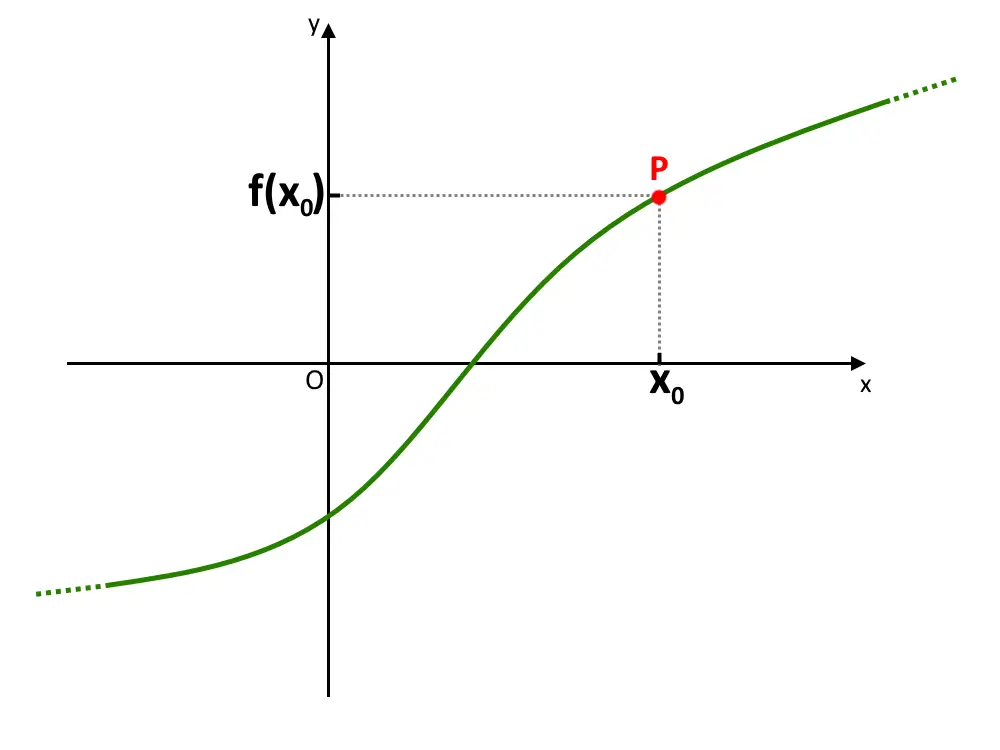
Quello che notiamo è che se io calcolo il limite sinistro di f(x) in x_0 , il valore di tale limite sarà proprio f(x_0)!
\lim\limits_{x \to x_0 ^- } f(x) = f(x_0)
Cosa significa questo? Fare il limite sinistro significa che la x va verso il punto x_0 da sinistra percorrendo il percorso della f(x) e, come vedete dall’immagine seguente, il limite (la freccetta) va a ricadere proprio sul punto P, cui corrisponde il valore di f(x_0) .
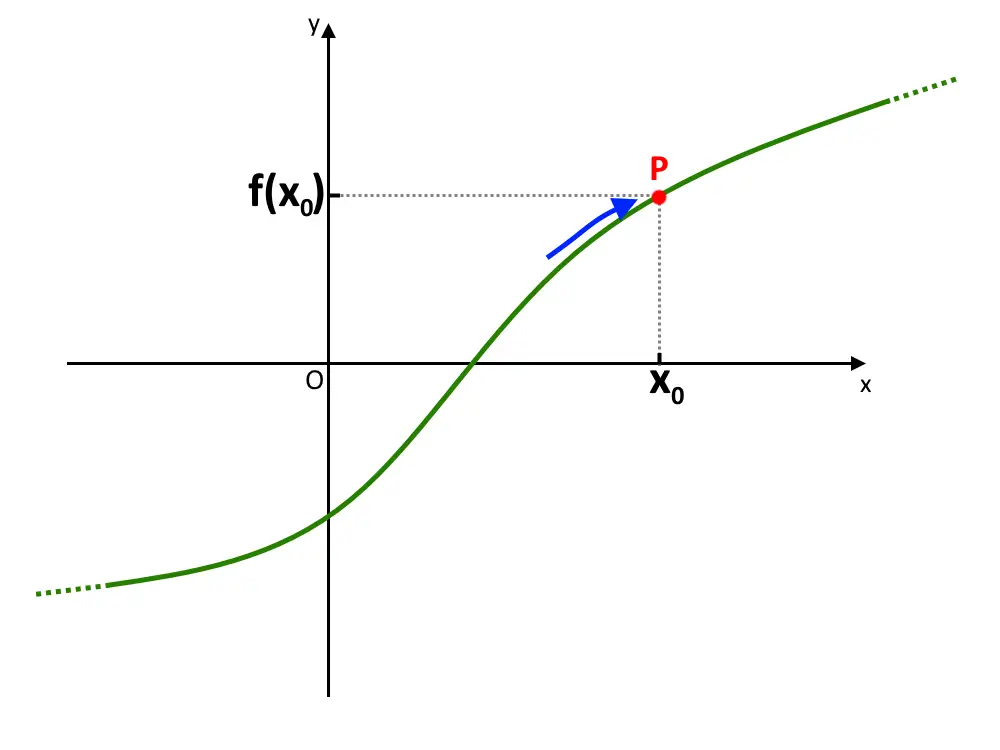
Anche se calcoliamo il limite destro, accade la stessa cosa: ossia la funzione f(x) anche da destra (la freccetta) ricade su punto P cui corrisponde sempre f(x_0) !
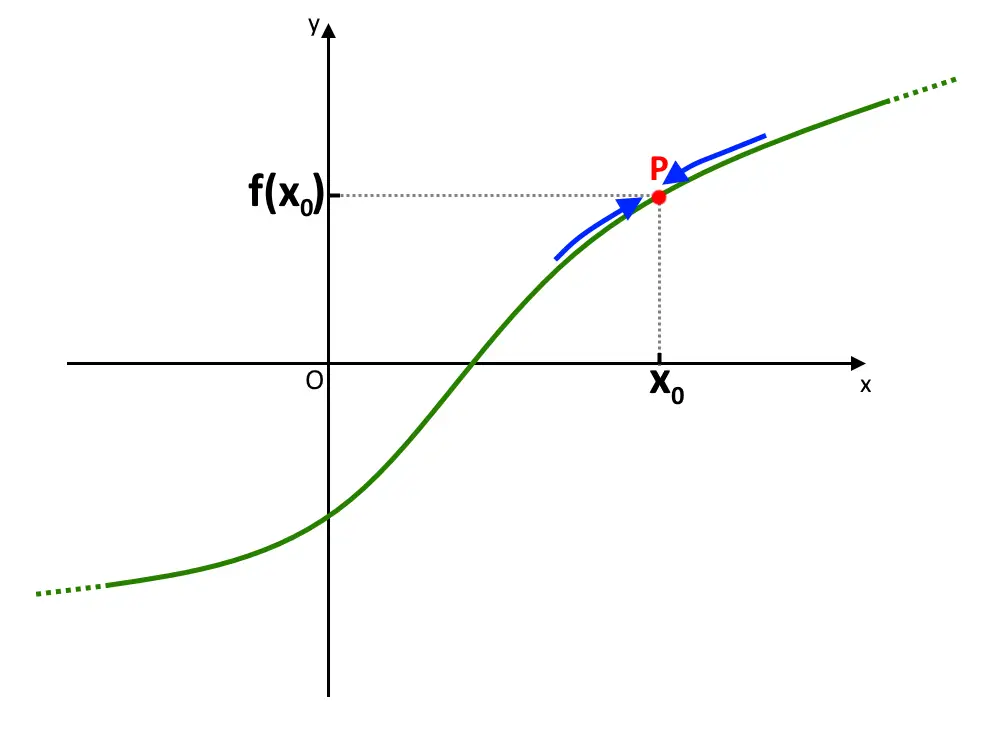
Una funzione che possiede tale caratteristica si dice che è continua nel punto x_0 . In formule è equivalente a dire che:
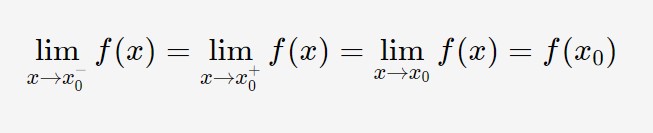
Queste formule sopra sono importanti, perché vi serviranno negli esercizi. Lo stesso significato si può esprimere anche in un modo più formale:

Ciò significa che preso un qualsiasi numero piccolo \epsilon (ad esempio 0,1), prendiamo un intorno di x_0 di raggio 0,1. In questo intorno per una qualsiasi x cui corrisponde f(x), la f(x) ricadrà vicino a f(x_0) , al massimo con una distanza appunto di \epsilon .
Per capire ancora meglio il tutto, è necessario a questo punto vedere allora quando si ha a che fare con funzioni non continue in un punto!
Funzione non continua in un punto
Ora che abbiamo visto cosa significa funzione continua in un punto, a questo punto rafforziamo tale concetto mostrando esempi in cui una funzione non lo è. Abbiamo detto che una f(x) presenta continuità in un punto se:
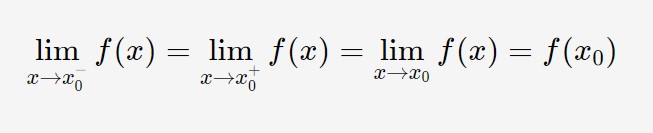
Che in parole povere significa che la freccetta, sia che parte da sinistra che da destra verso x_0, sempre va a finire nello stesso punto P di componenti (x_0 , f(x_0) ).
Quindi, quando una funzione non è continua in un punto? Quando la formula della continuità in un punto non è verificata, ossia se:
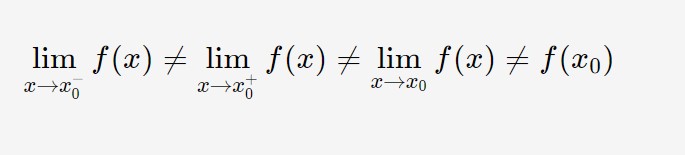
E questo cosa significa? Significa che la freccetta va a ricadere in un punto diverso, a seconda che parte da sinistra o da destra!
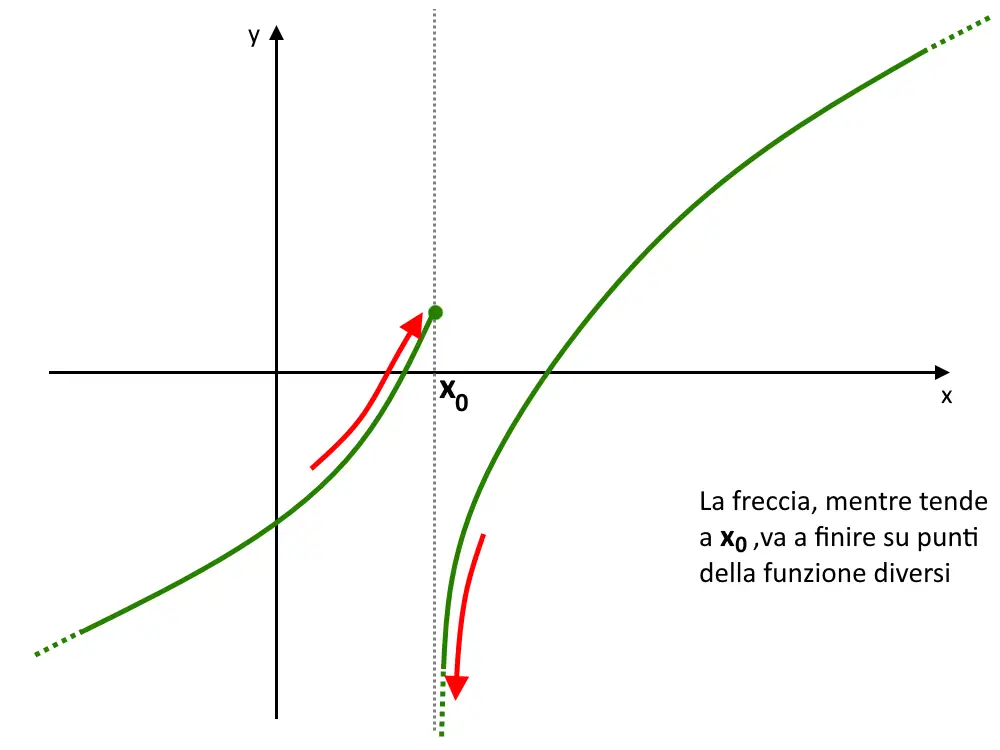
Vediamo alcuni esempi pratici, con calcoli per vedere come fare.
Esempi di funzioni continue in un punto
Esempio 1. Abbiamo la funzione f(x) = x^3 + 1 , vediamo se la f(x) è continua in x_0 = 2 .
Per verificare che una funzione sia continua in un punto, dobbiamo utilizzare la formula con i limiti:
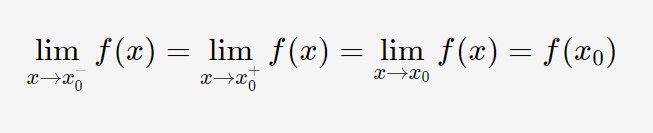
Calcoliamo il limite sinistro:
\lim\limits_{x \to x_0 ^- } f(x) = \lim\limits_{x \to 2^- } x^3 -1 = (2^-)^3 -1 = 8-1=7
Calcoliamo il limite sinistro:
\lim\limits_{x \to x_0 ^+ } f(x) = \lim\limits_{x \to 2^+ } x^3 -1 = (2^+)^3 -1 = 8-1=7
Come vediamo il limite sinistro e destro coincidono (cioè se vado da sinistra o da destra sempre a 7 arrivo). E di conseguenza la funzione è continua in tale punto. Ossia il cammino per arrivarci è “continuo, lineare”. Di fatti il grafico della funzione f(x) è il seguente.
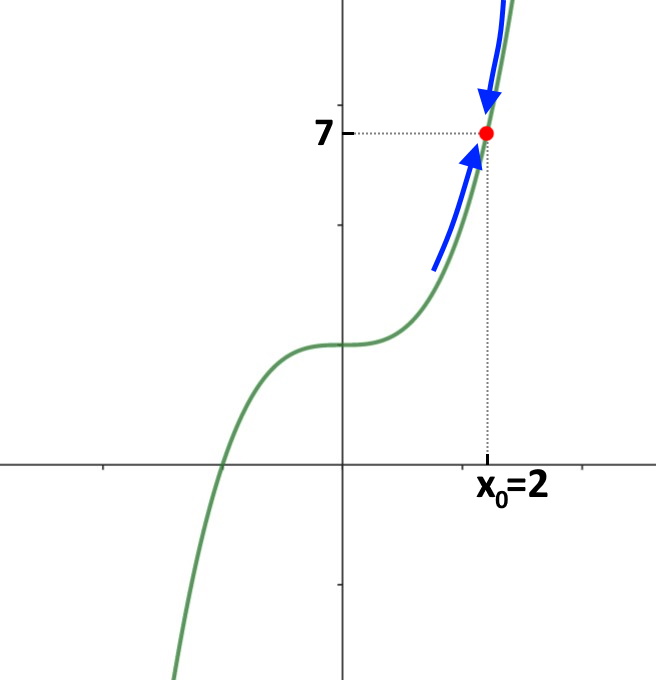
Esempio 2. Abbiamo la funzione f(x) = \ln (x+1) , vediamo se la f(x) è continua in x_0 = 0 .
Come detto prima, dobbiamo verificare che il limite sinistro e destro coincidano.
Calcoliamo quello sinistro:
\lim\limits_{x \to x_0 ^- } f(x) = \lim\limits_{x \to 0^- } \ln (x+1) = \ln (0^- +1) = \ln 1 = 0
E poi quello destro:
\lim\limits_{x \to x_0 ^+ } f(x) = \lim\limits_{x \to 0^+ } \ln (x+1) = \ln (0^+ +1) = \ln 1 = 0
I due valori coincidono: la funzione è continua in x=0! E ciò lo si può notare dall’immagine!
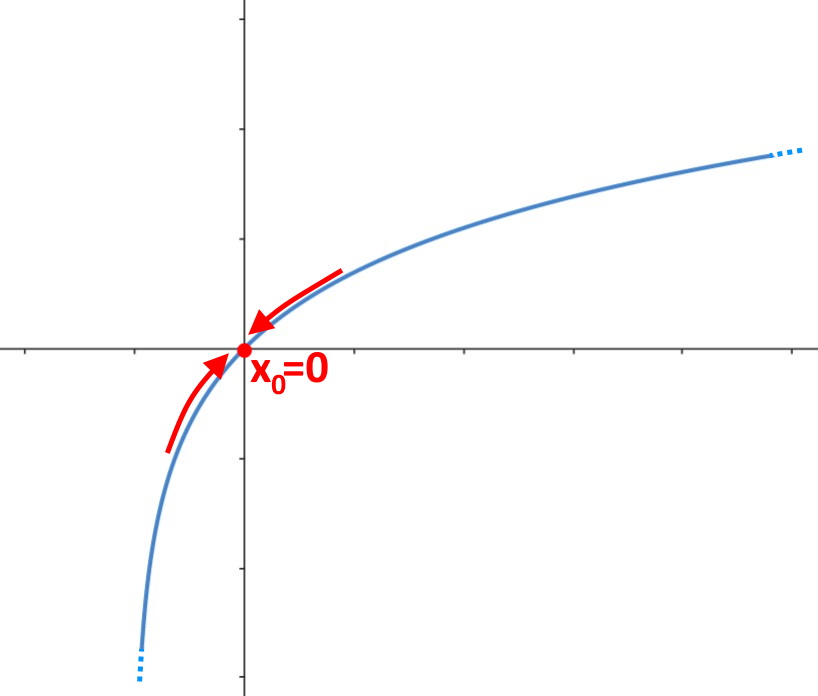
Esempio 2. Abbiamo la funzione f(x) = \begin{cases} 1\;\; se \; \; x<0 \\ x \;\; se \;\; x \ge 0 \end{cases} , vediamo se la f(x) è continua in x_0 = 0 .
Calcoliamo il limite sinistro di questa funzione. Il punto è 0^- e di conseguenza la f(x)=1 in tale intervallo! (questo perché 0^- sta in x<0) Quindi:
\lim\limits_{x \to x_0 ^- } f(x) = \lim\limits_{x \to 0^- } 1 = 1
In quello destro il punto è katex]0^+ [/katex] e quindi la funzione è f(x)=x in questo intervallo. Calcoliamo quindi tale limite:
\lim\limits_{x \to x_0 ^+ } f(x) = \lim\limits_{x \to 0^+ } x = 0
I due valori non coincidono, di conseguenza la funzione non è continua nel punto x=0, di fatti guardate l’immagine seguente della funzione!
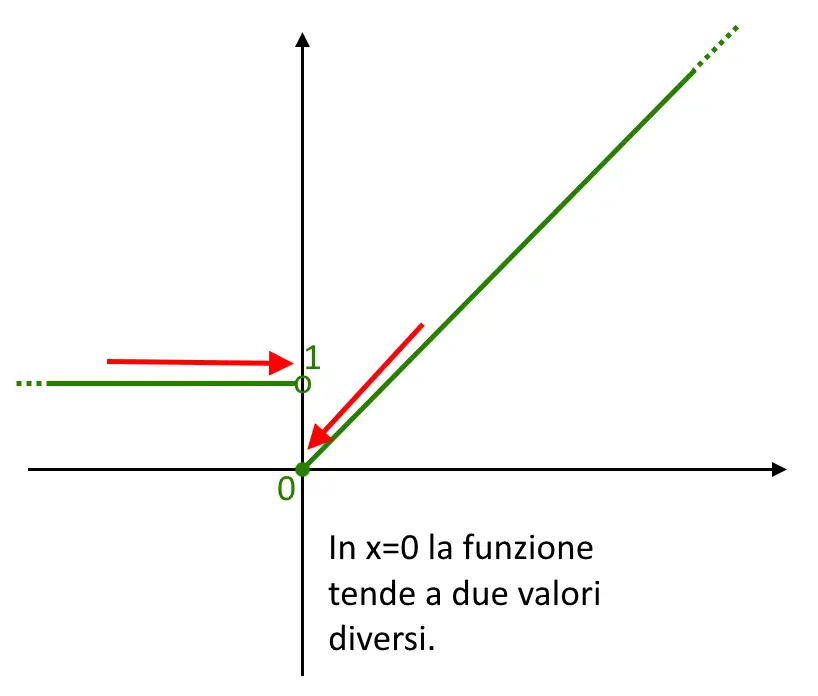
Adesso estendiamo il concetto di continuità a tutto il dominio, e non più ad un singolo punto.
Funzioni continue nel dominio
Consideriamo una funzione f(x) definita in un certo dominio [a,b]. Tale funzione si dice continua in tutto il dominio, se f(x) in ogni punto x_0 \in [a,b] è continua. In pratica stiamo semplicemente estendendo il concetto espresso prima: prima avevamo una f(x) continua in un punto, adesso stiamo dicendo che una f(x) è continua in tutto un intervallo se f(x) è continua in qualsiasi punto dell’intervallo.
Per esempio se consideriamo la f(x)=x , essa è continua in tutto il dominio suo ]-\infin , + \infin [ perché per qualsiasi punto, la f(x) è continua in quel punto!
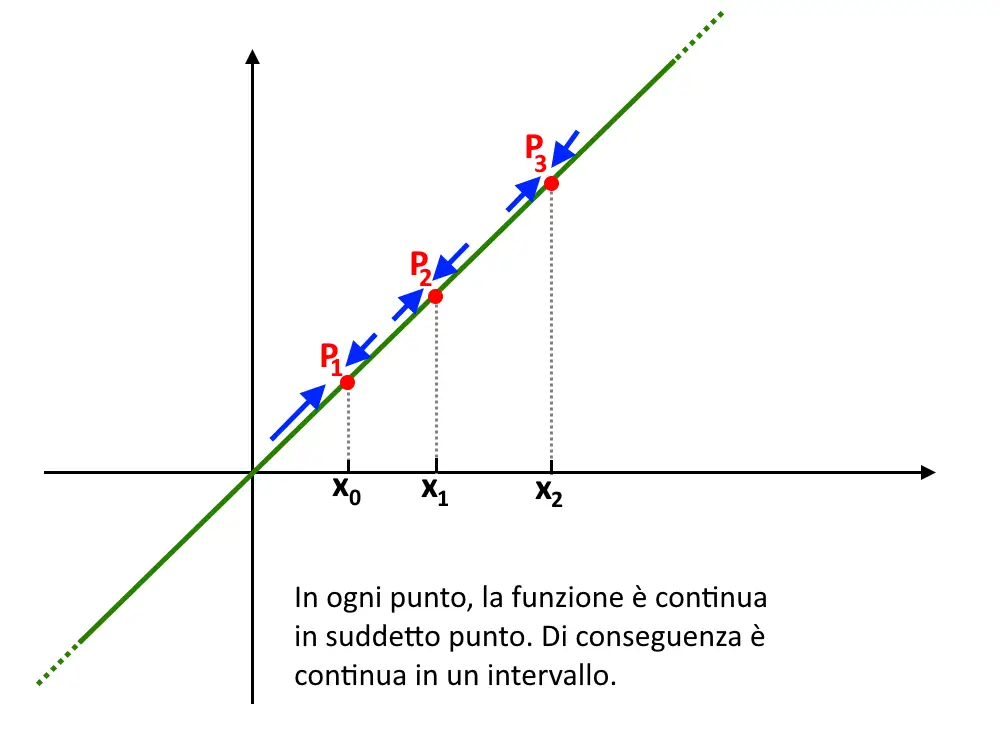
La pagina è conclusa.
E’ importante per gli esercizi sapere come fare i limiti base: trovate 30 esercizi svolti.
Trovate altri centinaia di argomenti e di esercizi svolti di matematica, geometria analitica e geometria!
Continuate a studiare sul nostro sito!
Per approfondire:
https://it.wikipedia.org/wiki/Funzione_continua#:~:text=Una%20funzione%20%C3%A8%20continua%20in%20un%20punto%20se%20e%20solo,continua%20a%20destra%20e%20a%20sinistra.&text=non%20esiste%20relazione%20d’ordine,%22%20o%20una%20%22sinistra%22.
funzioni
esercizi