Funzione composta: definizione, come calcolarla ed esempi
Funzione composta: in questa pagina vedremo la definizione, e poi tanti esempi su come calcolarla. Anche il calcolo del dominio richiede un discorso a parte, e non è una cosa banale. Poi vedremo che se due funzioni sono continue, anche la loro composta sarà continua. Ma iniziamo subito!
Indice
- Funzione composta: definizione
- Come calcolare una funzione composta
- Composta della funzione inversa
- Dominio di una funzione composta
Iniziamo subito!
Funzione composta: definizione
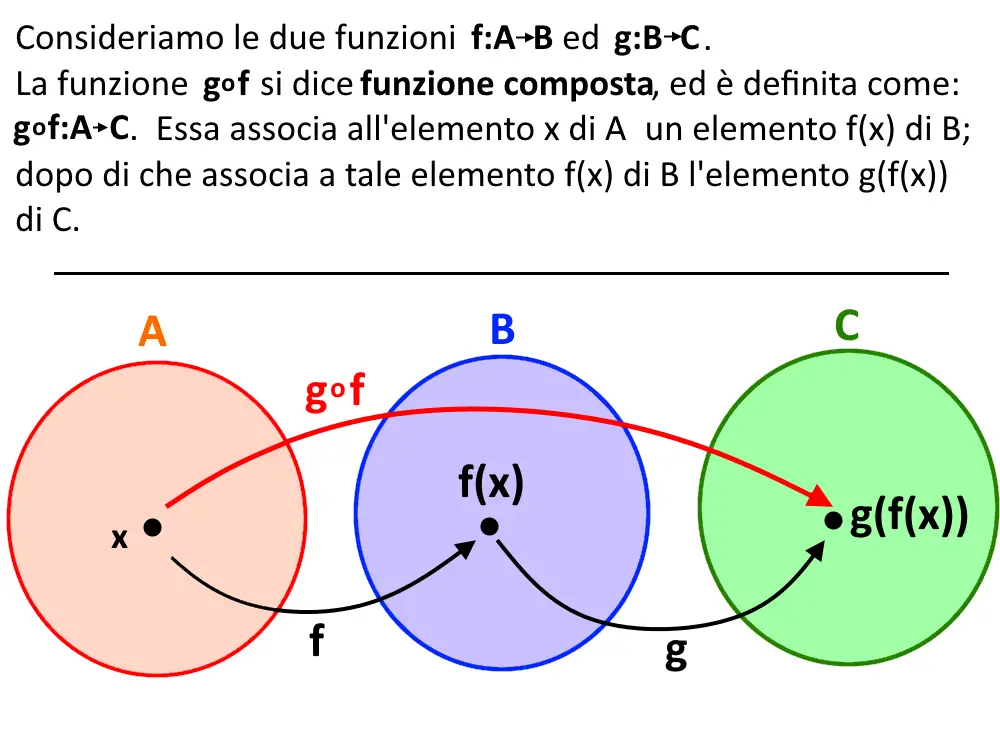
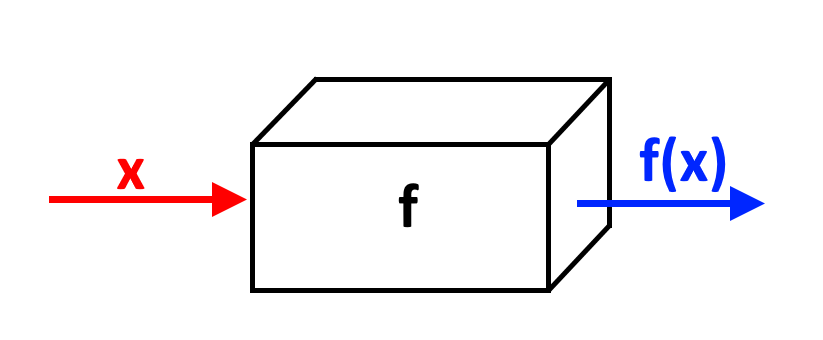
Cosa significa tutto questo in breve? Ricordiamo che una funzione f:A \to B è come una scatola: vi entra un “input”, questo input passa nella scatola e viene trasformata in “output” dalla scatola stessa. Se x è l’input, l’output è f(x). Osservate come si mette l’input dentro la f()!
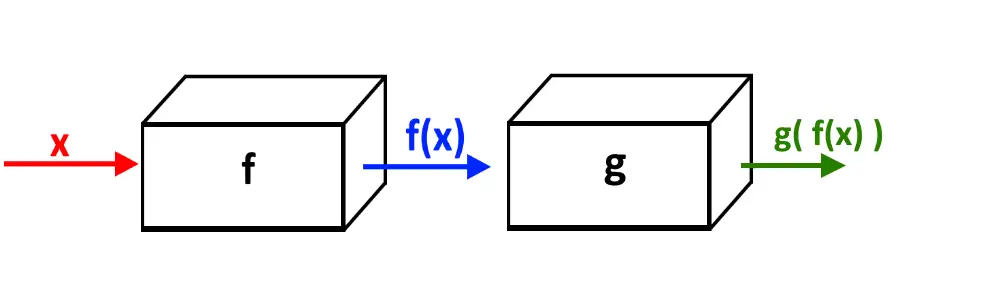
Una funzione composta invece passa per due scatole! Di conseguenza se dalla prima scatola esce f(x), questa f(x) adesso rappresenta l’input della seconda scatola…cioè quello che deve entrare nella seconda scatola! Di conseguenza quello che uscirà sarà un qualcosa del tipo g(). E dentro cosa ci mettiamo? Come detto prima, bisogna metterci l’input, che è f(x)!
E quindi uscirà fuori g(f(x))!
Vediamo adesso un esempio pratico per capire meglio!
Come calcolare una funzione composta
Sia f: \Reals \to \Reals e sia g: \Reals \to \Reals .
Dove di preciso f(x)=x+1 e g(x)=2x+2.
Calcoliamo la funzione composta g \circ f .
Come possiamo vedere, essendo che f: A \to B allora notiamo dalla traccia che A= \Reals , B= \Reals , ed anche g: B \to C fa sì che C= \Reals .
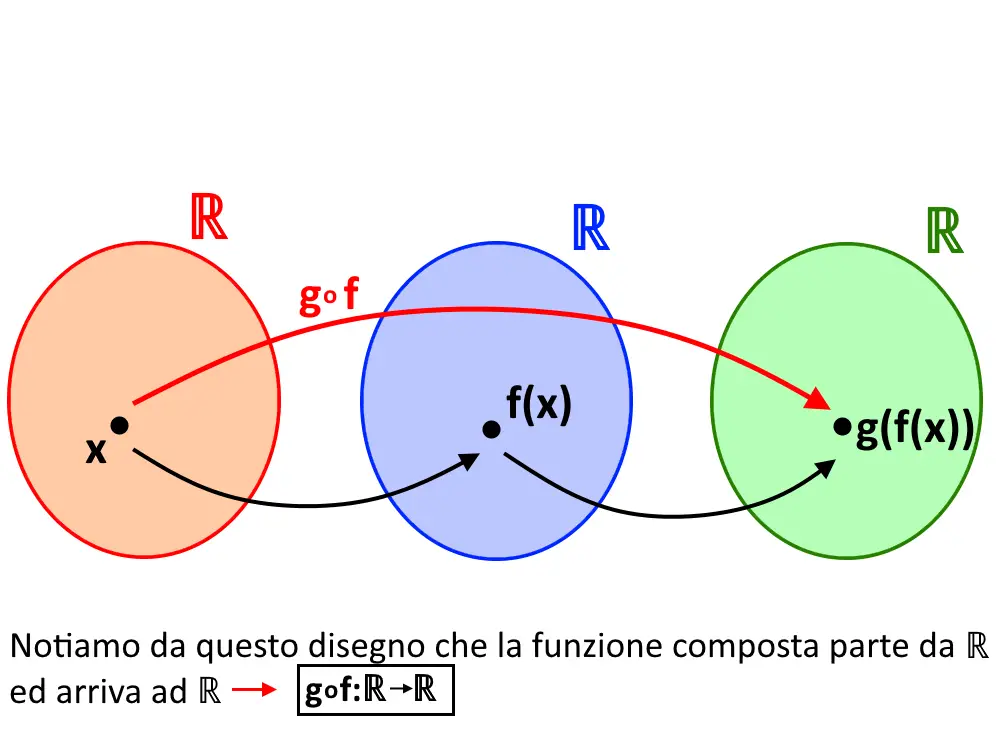
Visto che la funzione composta deve essere g \circ f : A \to C , allora sarà g \circ f : \Reals \to \Reals !
Ma chi è in pratica questa funzione composta? g(f(x)) come si calcola?
In pratica ciò che dobbiamo fare è partire dal considerare la g(x):
g(x)=2x+2
E per trovare g(f(x)), dobbiamo sostituire al posto della x la f(x):
g(f(x))=2(x+1)+2
Ed a questo punto semplificare il più possibile la funzione che è uscita fuori:
g(f(x))=2x+2+2
g(f(x))=2x+4
E questa è la funzione composta g \circ f (x)!
E se volessimo calcolare invece f \circ g (x) cosa esce fuori? La stessa cosa?
No, in genere g \circ f \ne f \circ g , ossia l’operazione di composizione di funzioni non è commutativa.
Riprendiamo lo stesso esempio, e calcoliamoci adesso f \circ g (x) .
Questa funzione composta, a livello di insiemi è f \circ g : C \to A che sarebbe sempre f \circ g : \Reals \to \Reals . Cioè rappresenta il percorso inverso!
Adesso ci dobbiamo calcolare la funzione composta f(g(x)). Quindi ora, al contrario, scriviamo:
f(x)=x+1
E sostituiamo al posto della x la g(x):
f(g(x))=(2x+2)+1
f(g(x))= 2x+3
E come possiamo vedere è diverso! Quindi l’ordine nella composizione di funzioni è importante!
Composta della funzione inversa
Sia f: A \to B , e sia la sua funzione inversa f^{-1} : B \to A . Cosa esce fuori se ci calcoliamo la composta della funzione e della sua inversa f^{-1} \circ f ?
Questo è molto particolare. Disegniamo gli insiemi per capire meglio. Seguiamo lo stesso ragionamento della definizione classica di funzione composta: partiamo dall’insieme A dove c’è un primo input x, questo passa per la prima scatola (f) che lo fa finire in B dove c’è f(x). Dopo di che vi è la scatola f^{-1} , che è una funzione inversa, ed è definita in modo tale da “ritornare indietro”: quindi f(x) entra nella seconda scatola f^{-1} ed esce fuori x un’altra volta!
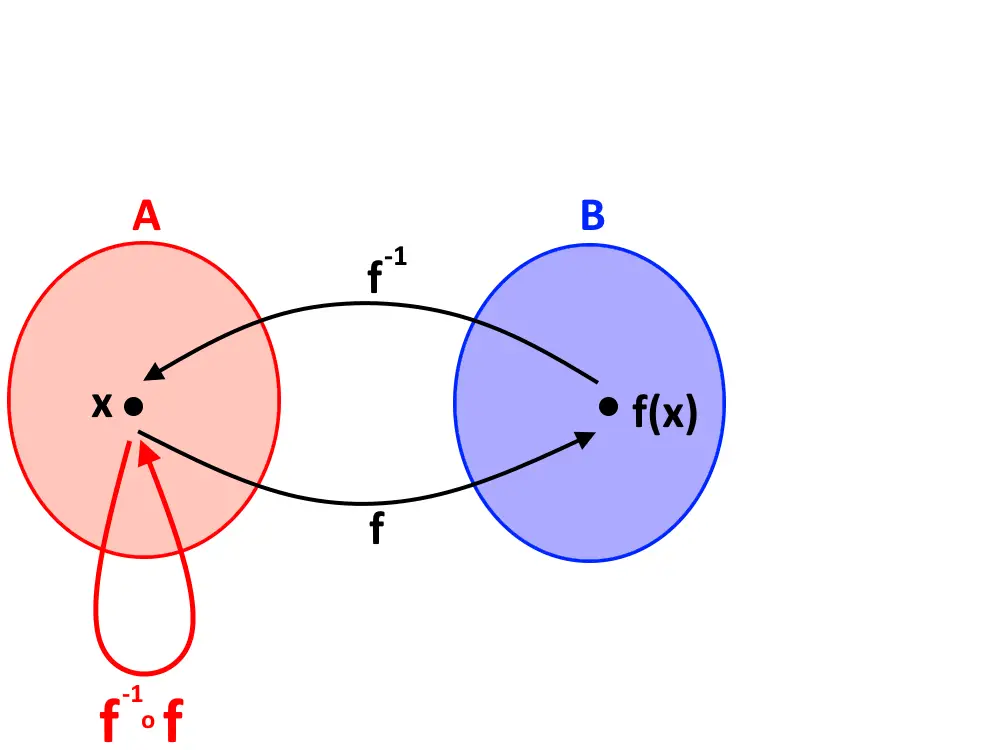
Questo vuol dire che la funzione composta risultante f^{-1} \circ f : A \to A !
Ciò implica, capibile dal disegno, che:
f^{-1} (f(x)) = x
E questo vale qualsiasi sia la funzione di partenza! La funzione inversa della funzione stessa è la x! O in altre parole, la composta della funzione e della sua inversa dà sempre la variabile iniziale x!
Questo vale anche se calcoliamo la composta f \circ f^{-1} …il percorso è inverso ma il risultato è sempre lo stesso!
Quindi anche:
f (f^{-1}(x)) = x
Di conseguenza qui, solo in questo caso, vale che la composizione di una funzione con la sua inversa è commutativa:
f^{-1} \circ f = f \circ f^{-1}
Facciamo adesso un esempio pratico per capire meglio ciò che abbiamo detto!
Esempio. Sia la funzione f(x)= e^x e la sua inversa, calcolare la loro composizione.
Calcolando la sua funzione inversa (cliccateci sopra per vedere come si fa) viene fuori che:
f^{-1}(x)= \ln x
Adesso proviamo a calcolare f \circ f^{-1} , ossia f (f^{-1}(x)) . Prendiamo in considerazione:
f^{-1}(x)= \ln x
E ci sostituiamo al posto della x la f(x):
f^{-1}(f(x))= \ln e^x
Applicando la proprietà dei logaritmi secondo cui:
\log_a b^n = n \log_a b
Allora, nel nostro caso, viene fuori che:
f^{-1}(f(x))= x \ln e
Ma il \ln e = 1 ! Di conseguenza otteniamo quello che ci aspettavamo:
f^{-1}(f(x))= x
Cioè la composizione ci ritorna a dare la x!
E stessa cosa otterremo se facessimo il contrario. Adesso proviamo a calcolare invece f^{-1} \circ f , ossia f^{-1} (f(x)) . Prendiamo in considerazione ora:
f(x)= e^x
E sostituiamo al posto della x la f^{-1}(x):
f(f^{-1}(x))= e^{\ln x }
Qui, per una proprietà degli esponenziali con logaritmi segue che:
f(f^{-1}(x))= x
Abbiamo ottenuto sempre la variabile di partenza ed abbiamo confermato il fatto che:
f^{-1} \circ f = f \circ f^{-1}
In questa sezione non abbiamo considerato gli insiemi nel dettaglio, questo perché il discorso del dominio richiede delle considerazioni particolari, che vedremo nella prossima sezione!
Dominio di una funzione composta
Fino ad ora non abbiamo parlato di dominio della funzione composta, questo perché richiede un’attenzione diversa. Consideriamo le due funzioni f(x)=\sqrt{x} e g(x)=x^2 .
Calcoliamo la funzione composta g \circ f . Partiamo da:
g(x)= x^2
E come sempre sostituiamo al posto della x la f(x):
g(f(x))= (\sqrt{x})^2
Radice ed esponente si semplificano, dunque otteniamo che la funzione composta è:
g(f(x))=x
Chi è il dominio di questa funzione? Essendo che c’è solo la x voi direste tutto R? Purtroppo non è così! Vediamo perché.
Per arrivare alla risposta basta esplicitare i loro insiemi dominio e codominio.
La radice quadrata f(x) = \sqrt{x} è definita nel modo seguente:
f: [0,+\infin [ \to [0,+\infin [
Mentre la g(x)= x^2 è definita come:
g: \Reals \to \Reals
Adesso la composizione g \circ f : A \to C che dominio ha?
Seguendo la definizione di funzione composta, A e C rappresentano l’insieme di partenza e l’insieme di arrivo, dunque:
g \circ f : [0,+\infin [ \to \Reals
E quindi possiamo notare come il dominio rimanga quello di partenza, ossia:
D: [0,+\infin [
Di conseguenza g(f(x)) avrà il seguente grafico.
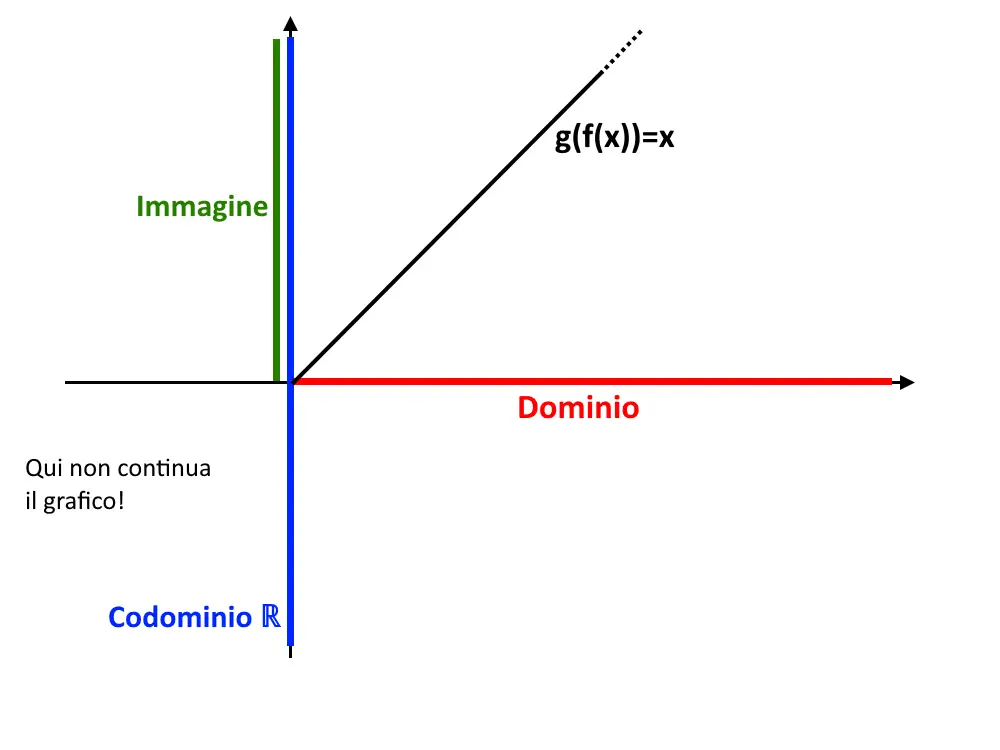
Sul dominio quindi bisogna prestare un’attenzione in più!
Notate come il codominio non corrisponde con l’immagine, quindi la funzione non è suriettiva! Molti libri confondono codominio ed immagine, quindi vi consiglio di leggere la pagina sulle funzioni suriettive. O spesso, per semplificare il tutto i libri fanno coincidere apposta codominio ed immagine.
La pagina è conclusa. Speriamo che sia stata esaustiva. Trovate comunque altri centinaia di argomenti ed esercizi svolti sia di matematica che di geometria analitica e geometria!
Continuate a supportare il sito!
pari e
dispari
esponenziali
esercizi