Equazioni fratte esercizi svolti
Esercizi svolti equazioni fratte! Per essere preparati per la verifica in classe sulle equazioni fratte basta uno o due giorni a studiare su questa pagina, e vedere come vengono svolti gli esercizi sulle equazioni fratte. Come vedete dall’indice, una parte sarà sulle equazioni fratte lineari, l’altra parte sarà sulle equazioni razionali fratte di secondo grado, cioè con la presenza di equazioni di secondo grado da risolvere alla fine.
Indice
- Condizioni di esistenza equazioni fratte
- Equazioni fratte di primo grado
- Equazioni fratte di secondo grado
- Equazioni fratte difficili
- Consigli generali da seguire
Vediamo innanzitutto come calcolare le condizioni di esistenza di una equazione fratta: passaggio importantissimo per risolverle!
Condizioni di esistenza
equazioni fratte
Il primo passaggio per risolvere le equazioni fratte è scrivere le condizioni di esistenza. Per una equazione fratta le condizioni di esistenza sono: scrivere il denominatore diverso da zero. E se abbiamo più denominatori? Allora dovremmo scrivere più condizioni di esistenza, e alla fine unirle con un sistema.
Vediamo subito con degli esempi come calcolare le condizioni di esistenza!
Esempio 1.
Iniziamo da questo esempio semplice. Abbiamo detto che le condizioni di esistenza è: denominatore diverso da zero.
Il denominatore è x+7 come potete vedere, e quindi:
CE:
Dobbiamo risolvere questa disuguaglianza. Una equazione con disuguaglianza si tratta proprio come se fosse un uguale, quindi non cambia nulla!
Isoliamo la x e viene:
CE:
Fatto! E poi la risoluzione dell’equazione la vediamo nel paragrafo successivo più giu!
Esempio 2.
Qui abbiamo invece più frazioni! Quindi dobbiamo scrivere più condizioni di esistenza, ed unirle con un sistema. Scriviamo perciò un sistema con la condizione di esistenza della prima frazione, e poi al secondo rigo del sistema la CE della seconda frazione, come segue:
CE:
CE:
Unire significa prenderle entrambe, e quindi la condizione di esistenza totale è semplicemente tutte e due insieme:
CE:
Esempio 3.
Qui state attenti! Abbiamo due frazioni ma a noi interessa solo quella con la x al denominatore! Quindi andiamo a considerare solamente la prima frazione chiaramente.
CE:
CE:
E così come per le equazioni di secondo grado, con solamente un numero, la soluzione è la radice con entrambi i segni:
CE:
Iniziamo ora a vedere come risolvere le equazioni fratte lineari con esercizi svolti!
Equazioni fratte di primo grado
esercizi svolti
Esercizio 1.
Come primissima cosa da fare SEMPRE nelle equazioni fratte, bisogna trovare le condizioni d’esistenza. Nel caso delle funzioni fratte, la condizione d’esistenza è: denominatore diverso da zero.
Qui per esempio abbiamo due frazioni, quindi due denominatori. Quindi in questo caso dobbiamo fare scrivere due condizioni d’esistenza:
CE: per quanto riguarda la prima frazione;
CE: per la seconda.
Quindi unendo le due condizioni, otteniamo chiaramente un’unica che è:
CE:
E solamente dopo fatto ciò possiamo passare alla risoluzione dell’equazione. In generale il secondo passo è ridurre tutto allo stesso denominatore, quindi facciamo un minimo comune multiplo ad ambo i membri:
Fatto ciò possiamo semplificare i due denominatori.
E come potete vedere ci siamo ricondotti ad una equazione lineare adesso, che sappiamo risolvere! Di fatti portiamo il 3x a primo membro (ricordandoci di cambiarlo di segno quando si passa da un lato all’altro).
Ora cambiamo tutto di segno, perchè vogliamo la x isolata per bene.
E poi dividiamo tutto per 2.
Ed abbiamo trovato la soluzione dell’equazione. Prima di concludere l’esercizio però bisogna controllare una cosa: se questo risultato fa parte delle condizioni di esistenza allora possiamo prendere questa soluzione per buona.
Le condizioni di esistenza ci dicono che x deve essere diverso da zero, noi abbiamo x=-2 e quindi vabenissimo!
Volendo, durante la verifica in classe visto che non avete il risultato del libro, per vedere se avete commesso errori potete effettuare la verifica dell’equazione, per controllare se le soluzioni sono giuste.
Esercizio 2.
Come abbiamo già detto: prima cosa scrivere le condizioni d’esistenza, ossia porre diversi da zero i denominatori. Partiamo dal primo denominatore:
CE:
Ora il secondo:
CE:
Unendo le due condizioni, troviamo una unica seguente.
CE:
In pratica per essere più chiari, le condizioni d’esistenza ti dicono quali valori la x può assumere! Ed è per questo che alla fine si controlla se la soluzione rientra nelle condizioni d’esistenza.
Torniamo all’esercizio, facciamo il minimo comune multiplo di tutti e due i membri:
Semplifichiamo ora i denominatori.
Nel primo membro possiamo applicare la formula del quadrato del binomio:
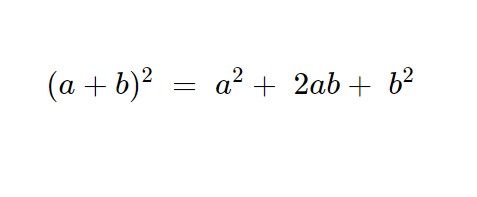
Quindi nel nostro caso viene, stando attenti ai segni:
Portiamo i termini con la x a primo membro, e gli altri al secondo. Ricordatevi di cambiare segno quando passate da una parte all’altra!
Sommiamo i termini comuni.
Cambiamo di segno tutto.
Poi dividiamo tutto per 15, ed il gioco è fatto!
Però attenzione! Controlliamo prima che questo risultato è accettabile, ossia rientra nelle condizioni d’esistenza…e di fatto rientra! Quindi vabene.
Esercizio 3.
Prima di scrivere le condizioni d’esistenza, notiamo subito una cosa: i due denominatori sono in realtà uguali ma di segno opposto. Cioè nel secondo denominatore possiamo scrivere mettendo un segno meno in evidenza:
Quindi la nostra equazione diventa:
Il segno – per il segno – del denominatore fa +, quindi viene:
Ed in questo modo abbiamo uno stesso denominatore, ci basta scrivere una sola condizione d’esistenza.
CE:
Adesso torniamo all’esercizio, facciamo il minimo comune multiplo.
Moltiplichiamo tutto per (x-8) così se ne va via il denominatore:
A questo punto ci basta risolvere questa equazione lineare:
La soluzione rientra anche nelle condizioni d’esistenza e quindi vabene come soluzione!
Continuiamo con altri esercizi svolti sulle equazioni fratte!
Esercizio 4.
Prima di fare qualsiasi calcolo date uno sguardo alla traccia dell’esercizio. Perchè vi potrebbe far risparmiare un po’ di inutili calcoli. Di fatti anche in questo caso notiamo che i due denominatori hanno un termine in comune, iniziamo a mettere in evidenza il 3:
Dopo di che, mettiamo anche in evidenza un segno meno come fatto nell’esercizio precedente:
Chiaramente ricordatevi dopo aver messo un segno meno in evidenza di cambiare anche i segni all’interno della parentesi. Comunque possiamo portare questo segno meno davanti alla frazione come segue:
A questo punto notiamo che apparte un 3, il denominatore è uguale. Quindi scriviamo una condizione d’esistenza, visto che il 3 è un numero positivo ed è ovvio che sia diverso da zero.
CE:
Ora possiamo andare a fare il minimo comune multiplo all’equazione:
Semplifichiamo i denominatori:
Ed ora sciogliamo le parentesi. State attenti che il segno meno cambia tutti i termini all’interno della parentesi di segno!
Che ha come soluzione x=0. Essa rientra anche nelle condizioni di esistenza, e quindi vabene come soluzione.
Esercizio 5.
Partiamo dalle condizioni d’esistenza come sempre. Per la prima frazione abbiamo semplicemente:
CE:
Per la seconda invece:
CE:
Ora, possiamo passare a fare il minimo comune multiplo ad ambo i membri.
Semplifichiamo i denominatori:
E poi svolgiamo le parentesi:
Ricordatevi una cosa: come prova del 9 per vedere se vi trovate, visto che non avete fatto ancora le equazioni di secondo grado allora i termini con la se ne devono andare via; se ciò non accade avete fatto qualche piccolo errore ed andate a ricontrollare.
E questa è la soluzione, essa rientra nelle condizioni d’esistenza? No. Le condizioni di esistenza ci dicono che la x deve essere diversa da e quindi la soluzione che abbiamo trovato non vabene: il risultato quindi è impossibile.
Continuiamo con altri esercizi svolti sulle equazioni fratte!
Esercizio 6.
Anche in questo caso possiamo notare, vedendo la traccia, che nell’ultimo denominatore possiamo mettere in evidenza una x:
In questo modo abbiamo due termini per il quale calcolare le condizioni d’esistenza, ossia la x e il termine (3x-1).
CE:
CE:
E quindi abbiamo in sintesi che le condizioni di esistenza dell’equazione è:
CE:
Ora possiamo tranquillamente passare al passaggio successivo: minimo comune multiplo di ambo i membri.
Passaggio successivo: semplificare i denominatori.
Svolgiamo la moltiplicazione della parentesi:
Sommiamo i termini comuni:
E quindi la soluzione trovata è x=0. Le condizioni di esistenza però ci dicono che questa non può essere presa, e quindi l’equazione non ha soluzione: essa è impossibile.
Esercizio 7.
Anche in questo caso spicca all’occhio i segni opposti dei denominatori, e quindi prima di tutto mettiamo in evidenza un segno meno in uno dei denominatori:
E portiamo il segno – davanti alla frazione.
A questo punto calcoliamo l’unica condizione d’esistenza dell’esercizio.
CE:
Passiamo al passaggio successivo: minimo comune multiplo come sempre! Attenzione ai segni adesso, fate un passaggio alla volta con calmissima.
Semplifichiamo i due denominatori:
Sciogliamo la parentesi prestando attenzione a cambiare il segno anche al 4, non scordatevelo.
Il risultato è concorde con la condizione d’esistenza e quindi vabene questa soluzione.
Continuiamo con altri esercizi svolti sulle equazioni fratte!
Esercizio 8.
Questo è un esercizio modello ed alla fine capirete il perchè.
Primo punto che ormai abbiamo imparato: condizioni d’esistenza.
CE:
Adesso possiamo passare a fare il minimo comune multiplo:
Passiamo a semplificare entrambi i denominatori ed otteniamo:
Facciamo la moltiplicazione con la parentesi tonda adesso.
Quando viene fuori questo risultato, si scrive che la soluzione è indeterminata, con , ossia la CE.
Esercizio 9.
Prima di passare alle condizioni di esistenza, come già detto, bisogna dare uno sguardo ai denominatori e cercare di trovare (se c’è) un modo per renderli simili. In questo caso per la seconda frazione, possiamo sfruttare la formula della differenza di quadrati:
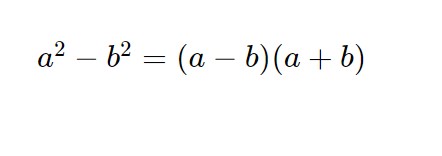
E quindi nel nostro caso:
Sostituiamo tale risultato nell’equazione.
Ed ora possiamo finalmente trovare le condizioni d’esistenza.
CE:
CE:
Ed in conclusione abbiamo:
CE:
Passiamo al m.c.m. di ambo i membri ora:
Semplifichiamo ed otteniamo:
Svolgiamo la moltiplicazione della prima parentesi e della terza, mentre per la seconda ci ricordiamo direttamente che:
E quindi:
E dividendo tutto per -2, otteniamo chiaramente x=0. E questa rispetta anche le CE.
Esercizio 10.
Qui la condizione d’esistenza è immediata.
CE:
Secondo step: minimo comune multiplo di tutto.
Semplifichiamo i denominatori:
Svolgiamo le parentesi:
Portiamo i termini ai corrispettivi posti:
Ed anche in questo caso, quando viene un risultato del genere si scrive: soluzione indeterminata con CE:
Continuiamo con altri esercizi svolti sulle equazioni fratte!
Equazioni fratte di secondo grado
esercizi svolti
Esercizio 11.
Dire equazioni fratte di secondo grado significa semplicemente che abbiamo a che fare con equazioni fratte, ma con la presenza di termini di secondo grado, e quindi andremo a risolvere anche una equazione di secondo grado alla fine.
Il procedimento è lo stesso per grossi punti: il primo è quello di calcolare le condizioni di esistenza anche qui.
CE:
CE:
Quindi solo x diverso da zero. Adesso come negli altri esercizi, passiamo a fare il minimo comune multiplo:
E semplifichiamo entrambi i denominatori:
Ora, ricordandoci di come si svolgono le equazioni di secondo grado, portiamo tutto a primo membro, cercando di arrivare alla forma seguente:
Se non vi ricordate i discriminanti ecc. vi consiglio di vederli nella pagine in blu sopra segnata. Comunque, essendo il coefficiente b dispari calcoliamo il Delta con la formula:
Il discriminante è positivo, e quindi ci aspettiamo due soluzioni distinte, calcolabili tramite:
E quindi le due soluzioni sono:
Entrambe le soluzioni rispettano le CE, e quindi le prendiamo entrambe come soluzioni dell’esercizio!
Esercizio 12.
Scriviamo le condizioni di esistenza.
CE:
CE:
E quindi abbiamo in sintesi:
CE:
Adesso facciamo il mcm.
Semplifichiamo i denominatori.
E svolgiamo la parentesi.
Portiamo tutto a primo membro, come prima:
A questo punto si può risolvere in due modi. Il primo modo è applicare lo stesso la formula di prima e calcolare il discriminante ecc. Il secondo modo che è quello più veloce è quello di mettere in evidenza la x:
E questa notiamo che può essere uguale a zero se un termine o l’altro è uguale a zero, ossia se:
E queste due sono anche le soluzioni dell’esercizio. Chiaramente controlliamo se rispettano le CE e sì: le rispettano, sono le soluzioni!
Continuiamo con altri esercizi svolti sulle equazioni fratte!
Equazioni fratte esercizi difficili
Esercizio 13.
Qui con qualche passaggio algebrico possiamo rendere i due denominatori uguali, di fatti mettendo in evidenza nella seconda frazione il termine viene:
Poi razionalizziamo solamente il termine . Facciamolo un attimo separatamente qui:
E quindi sostituendo questo risultato nell’equazione otteniamo:
E così facendo abbiamo ottenuto due denominatori con i termini con l’incognita uguali, quindi facciamo un solo CE.
CE:
Adesso passiamo finalmente al mcm:
Semplifichiamo i lunghi ahimè denominatori:
Portiamo tutto a primo membro, come vedete quando gli esercizi sono lunghi: pazienza e fate un passaggio alla volta!
Calcoliamo adesso il discriminante con la classica formula a noi nota:
Se fate questo conto su calcolatrice, ci rendiamo conto che il Delta è negativo, e quindi non esiste nessuna soluzione.
Esercizio 15.
Mettiamo innanzitutto in evidenza il 2 nella seconda frazione:
E quindi abbiamo solo la seguente condizione d’esistenza:
CE:
Passiamo al minimo comune multiplo come sempre:
Moltiplichiamo tutto per 2(x-1) in modo da levarci da mezzo il denominatore e ricondurre tutto a:
Mettendola in ordine, come vi consiglio sempre di fare:
Calcoliamo il discriminante.
E poi le due soluzioni distinte:
Ed allora abbiamo che le due soluzioni sono:
Però attenzione! Controllando le CE, la soluzione x=1 non possiamo prenderla. Ed allora prendiamo solamente x=-4 come soluzione dell’esercizio!
Vediamo dei consigli sugli esercizi delle equazioni fratte!
Consigli generali

Abbiamo fatto insieme tanti esercizi sulle equazioni fratte, vi consigliamo anche di fare esercizi sulle equazioni di secondo grado, per essere pronti al meglio per la verifica!
Continuate a studiare sul nostro sito e a fare altri esercizi di matematica che altro ancora!
Per approfondire: https://it.wikipedia.org/wiki/Equazione_fratta
disequazioni
esercizi
grafico
disequazione