Esercizi equazioni con valore assoluto
Esercizi equazioni con valore assoluto: 15 esercizi SVOLTI! Risolveremo le equazioni con valore assoluto spiegando ogni singolo passaggio con calma ed uno alla volta! Prima però è necessario che sappiate fare o almeno vi ricordate bene o male come si fanno le equazioni di secondo grado, e le disequazioni. Ma anche se non vi ricordate, iniziamo comunque! Partiamo dall’indice.
Indice
- Equazioni della forma: |f(x)| = k
- Equazioni della forma: |f(x)| = g(x)
- Equazioni della forma: |f(x)| = |g(x)|
- Equazioni con valore assoluto con parametri
Iniziamo subito con gli esercizi equazioni con valore assoluto !
Esercizi equazioni con valore assoluto della forma:
|f(x)| = k
Esercizio 1. 3 - |x-2| = 1
Quello che vogliamo fare, vedendo la traccia dell’esercizio, è ricondurci alla forma seguente di equazione con valore assoluto.
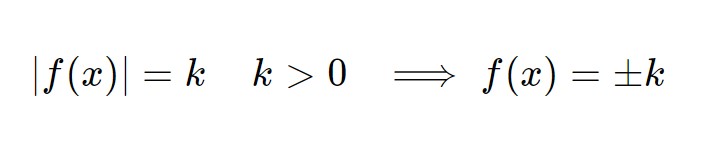
Quindi isoliamo il valore assoluto e portiamo il 3 a secondo membro:
- |x-2| = 1-3
- |x-2| = -2
A questo punto, cambiamo tutto di segno e ci siamo ricondotti esattamente alla forma sopra citata.
|x-2| = 2
E quindi per la risoluzione tutto ciò che dobbiamo fare è seguire la formula. Quindi segue che:
x-2 = \pm 2
Il \pm non deve spaventare: semplicemente dobbiamo risolvere due equazioni separate. Una contenente il segno + ed una col segno -. Quindi le seguenti:
x-2 = + 2
x-2 = - 2
Ognuna delle quali ci darà una soluzione. Partiamo dalla prima!
x-2 = + 2
Portiamo il -2 a secondo membro cambiandolo di segno non dimenticatevi:
x = 4
Ed abbiamo trovato così la prima soluzione dell’esercizio! Passiamo alla seconda equazione:
x-2 = - 2
Facciamo lo stesso:
x = - 2+2
x = 0
Ed abbiamo trovato anche la seconda soluzione. Abbiamo concluso l’esercizio, e le due soluzioni di esso sono:
x=4 \lor x=0
Volendo, durante la verifica in classe visto che non avete il risultato del libro, per vedere se avete commesso errori potete effettuare la verifica dell’equazione, per controllare se le soluzioni sono giuste.
Esercizio 2. |x^2 - 4x| -5 = 0
Dobbiamo sempre ricondurci alla forma dell’esercizio precedente. Quindi come prima cosa isoliamo il valore assoluto.
|x^2 - 4x| = 5
A questo punto possiamo applicare la formula per la risoluzione!
x^2 - 4x = \pm 5
E quindi dobbiamo risolvere due equazioni separate:
x^2 - 4x = + 5
x^2 - 4x = - 5
E quindi come potete vedere abbiamo due equazioni di secondo grado, che vi invito un attimo a vedere prima di procedere se non vi ricordate le formule. Iniziamo dalla prima:
x^2 - 4x = + 5
x^2 - 4x - 5 = 0
A questo punto possiamo andarci a calcolare il Delta. Essendo il coefficiente b pari usiamo la formula seguente:
\frac{\Delta}{4} = (\frac{b}{2})^2 -ac = 4+5=9
Il discriminante è positivo, e quindi ci aspettiamo due soluzioni distinte che sono:
x_{1,2} = \frac{- \frac{b}{2} \pm \sqrt{\frac{\Delta}{4}} }{a} = \frac{2 \pm 3 }{1}
E quindi:
x_1 = 2 + 3 = 5
x_2 = 2 - 3 = -1
Abbiamo calcolato le prime due soluzioni dell’esercizio! Ora passiamo all’altra equazione che ci rimane!
x^2 - 4x = - 5
x^2 - 4x + 5 = 0
Calcoliamo il discriminante un’altra volta:
\frac{\Delta}{4} = (\frac{b}{2})^2 -ac = 4-5=-1 <0
Abbiamo Delta<0, e quindi ciò significa che non esiste soluzione!
Le uniche due soluzioni dell’esercizio sono quindi:
x = -1 \lor x = 5
Esercizio 3. 3 + |2x^2 +9x | = -15
Come primo punto: isoliamo il valore assoluto.
|2x^2 +9x | = -15-3
|2x^2 +9x | = -18
Questa volta però notiamo una differenza! Nella formula notiamo che k>0, qui invece è <0! Un valore assoluto per definizione è positivo o al massimo uguale a zero, ma mai negativo. Questo significa che non può mai essere =-18. Quindi qui non c’è soluzione: è impossibile!
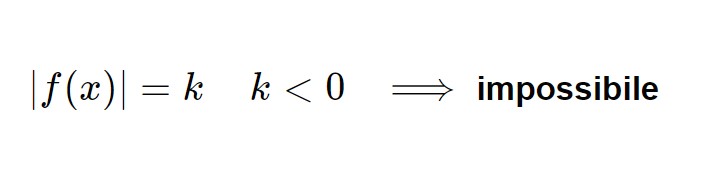
Esercizio 4. - | 6 - \frac{9}{x-2} | +3 = 0
Isoliamo sempre prima il valore assoluto:
- | 6 - \frac{9}{x-2} | = -3
Cambiamo tutto di segno:
| 6 - \frac{9}{x-2} | = 3
Qua notate che c’è soluzione perchè qui k>0. A questo punto prima di procedere, visto che abbiamo a che fare con una equazione fratta, dobbiamo trovare le condizioni di esistenza! Ossia denominatore diverso da zero:
CE: x-2 \ne 0 \implies x \ne 2
Ora possiamo procedere applicando la solita formula!
6 - \frac{9}{x-2} =\pm 3
Dobbiamo quindi risolvere separatamente due equazioni fratte:
6 - \frac{9}{x-2} = 3
6 - \frac{9}{x-2} = - 3
Iniziamo dalla prima, facciamo il minimo comune multiplo ad ambo i membri:
\frac{6(x-2)-9}{x-2} = \frac{3(x-2)}{x-2}
Semplifichiamo i denominatori (vi ricordo di cliccare sulla pagina delle equazioni fratte se non vi ricordate come si fanno):
6(x-2)-9 =3(x-2)
Sciogliamo le parentesi:
6x-12-9 =3x-6
6x-3x = -6 + 12 + 9
E quindi:
3x = 15
x=5
Abbiamo ottenuto la prima soluzione! Essa rispetta anche le condizioni di esistenza e quindi vabene! Passiamo alla seconda equazione:
6 - \frac{9}{x-2} = - 3
Facciamo il minimo comune multiplo.
\frac{6(x-2)-9}{x-2} = \frac{-3(x-2)}{x-2}
Semplifichiamo i denominatori:
6(x-2)-9 = -3(x-2)
6x-12-9 = -3x+6
Portiamo le x da una parte e il resto a secondo membro:
9x = 27 \implies x=3
Anche questa soluzione va bene perchè rispetta le CE! Abbiamo quindi che le soluzioni dell’esercizio sono:
x=3 \lor x= 5
Esercizio 5. 4 - | 25x^2 -5 | = 0
Iniziamo sempre dall’isolare il valore assoluto.
- | 25x^2 -5 | = -4
E poi non dimentichiamoci di cambiare segno, vogliamo il valore assoluto positivo, come in formula.
| 25x^2 -5 | = 4
E quindi abbiamo che:
25x^2 -5 = \pm 4
Dobbiamo quindi risolvere due equazioni di secondo grado:
25x^2 -5 = + 4
25x^2 -5 = - 4
Non spaventiamoci ed iniziamo con calma dalla prima.
25x^2 -5 = + 4
Questa la risolviamo comodamente portando i numeri a secondo membro:
25x^2 = + 4+5
25x^2 = 9
Poi isoliamo la x dividendo per 25:
x^2 = \frac{9}{25}
Ed infine facciamo la radice a tutto, ricordandoci di mettere un segno \pm!
x = \pm \sqrt{\frac{9}{25}}
x = \pm \frac{3}{5}
Abbiamo così le prime due soluzioni! Passiamo analogamente all’altra equazione, cui seguirà lo stesso procedimento: provate a farlo voi!
25x^2 -5 = - 4
25x^2 = 1
Isoliamo la x come fatto prima e poi facciamone la radice.
x^2 = \frac{1}{25}
x = \pm \frac{1}{5}
Ed ecco le altre due soluzioni! Come potete vedere le equazioni con valore assoluto richiedono molto spesso gli altri tipi di equazioni fatte quest’anno o negli anni precedenti!
La soluzione dell’esercizio è:
x= \pm \frac{1}{5} \lor x = \pm \frac{3}{5}
Continuiamo con altri esercizi equazioni con valore assoluto!
Esercizi equazioni con valore assoluto della forma:
|f(x)| = g(x)
Esercizio 6. | 4 -x | = 3 - 2x
Questa è una equazione con valore assoluto della seguente forma. La differenza con prima è che qui anche a secondo membro abbiamo delle x, mentre prima avevamo solo numeri.
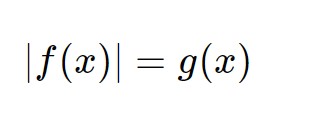
Quando abbiamo un esercizio del genere, bisogna risolvere i seguenti sistemi e trovarne le soluzioni:
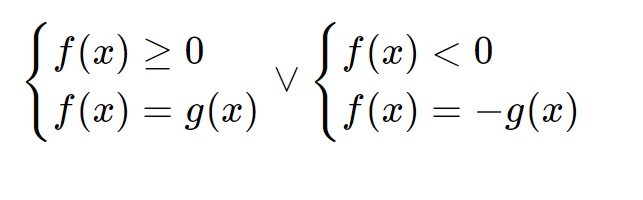
In questo esercizio abbiamo già l’equazione nella forma |f(x)| = g(x) e di conseguenza possiamo già seguire la formula appena sopra scritta ed andare a risolvere due sistemi:
\begin{cases} 4-x \ge 0 \\ 4 -x = 3 - 2x \end{cases} \lor \begin{cases} 4-x<0 \\ 4 -x = -3 + 2x \end{cases}
Non spaventiamoci! Ora vi faremo vedere come si calcola! Una alla volta, portiamo le x a primo membro e gli altri numeri a secondo membro.
\begin{cases} -x \ge -4 \\ -x+2x = 3 -4 \end{cases} \lor \begin{cases} -x<-4 \\ -x-2x = -3 -4 \end{cases}
Cambiamo di segno dove la x ha un segno-, e ricordatevi che in una disequazione quando cambiate tutto di segno anche il segno della disequazione cambia ( ad esempio da < diventa > ):
\begin{cases} x \le 4 \\ x = -1 \end{cases} \lor \begin{cases} x>4 \\ -3x = -7 \end{cases}
Ci rimane l’ultimo termine, nel quale cambiamo di segno e dividiamo per 3 ed abbiamo finito:
\begin{cases} x \le 4 \\ x = -1 \end{cases} \lor \begin{cases} x>4 \\ x = \frac{7}{3} \end{cases}
Ora avviene il passaggio successivo: disegniamo con un grafico dei segni il primo sistema.
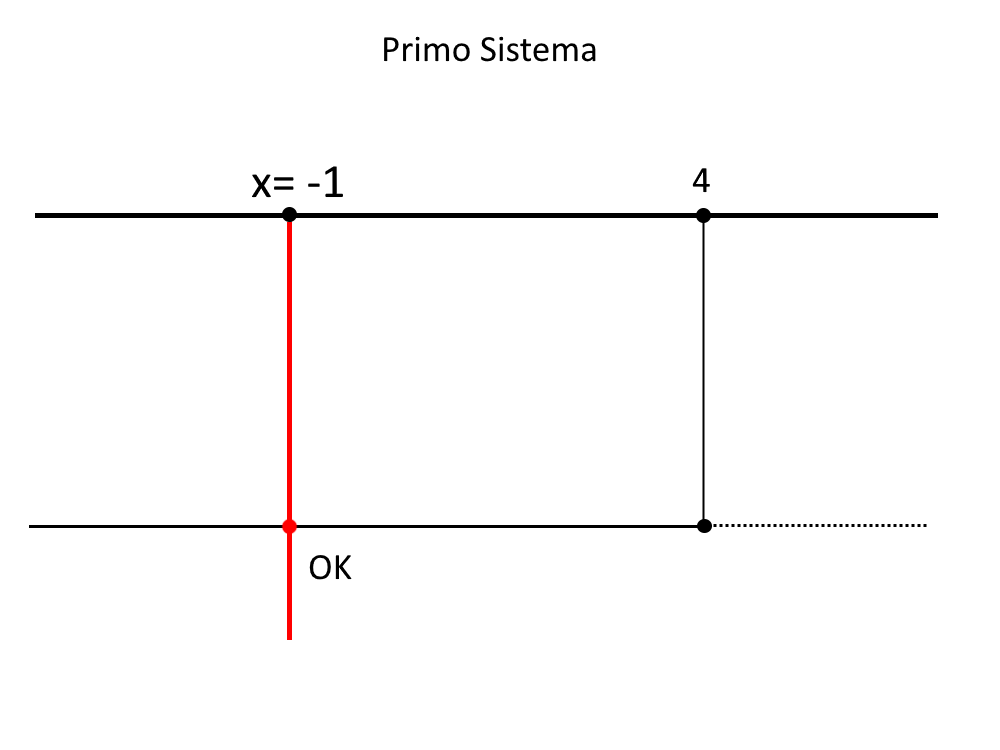
Ora, se la soluzione x=-1 cade nell’intervallo della disequazione, allora tale soluzione è accettabile, altrimenti no.
In questo caso notiamo che la soluzione x=-1 cade nell’intervallo della disequazione, e quindi è accettabile!
Passiamo al secondo sistema con un altro grafico dei segni.
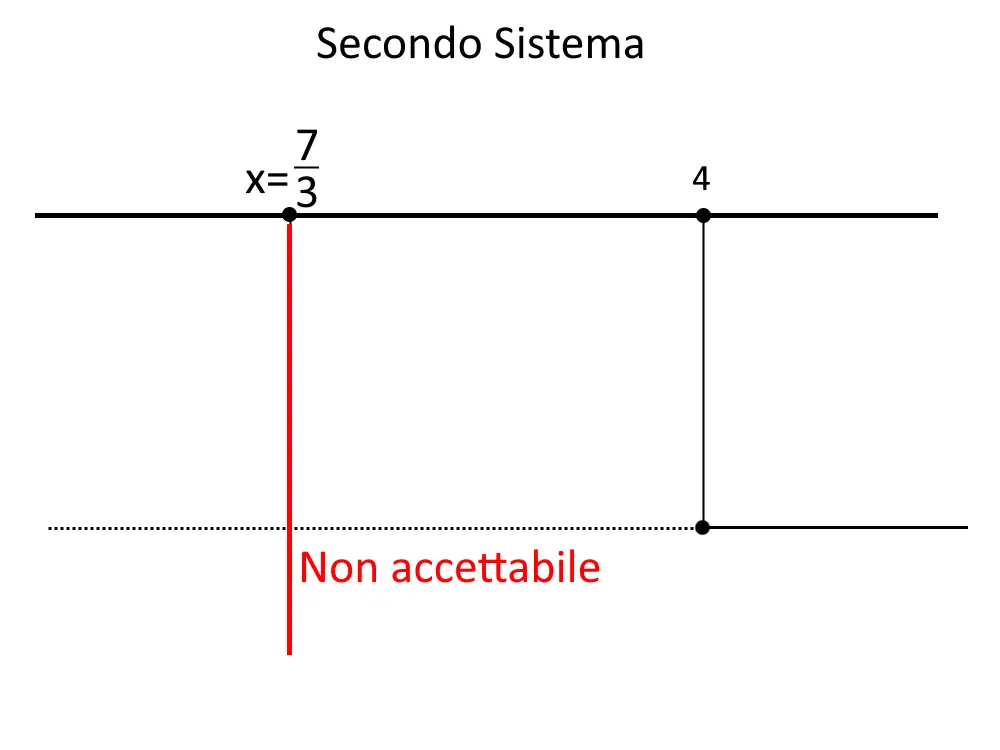
Qui invece notiamo che la soluzione non cade in nessun intervallo! Quindi questa non la prendiamo! Non è accettabile!
L’unica soluzione dell’esercizio è quindi x=-1.
Esercizio 7. | x^2 - 2x | = 3x
Stesso caso di prima: andiamo a risolvere i seguenti sistemi:
\begin{cases} x^2 - 2x \ge 0 \\ x^2 - 2x = 3x \end{cases} \lor \begin{cases} x^2 - 2x<0 \\ x^2 - 2x = -3x \end{cases}
Da ora in poi dobbiamo stare attenti, perchè gli esercizi non sono difficilissimi, ma prevedono tanti calcoli. L’importante è capire come funziona il tutto!
Nelle due disequazioni notiamo che possiamo mettere in evidenza una x per la risoluzione. (Come visto nell’esercizio 8 della pagina disequazioni di secondo grado).
\begin{cases} x(x - 2) \ge 0 \\ x^2 - 2x - 3x=0 \end{cases} \lor \begin{cases} x(x - 2) <0 \\ x^2 - 2x +3x=0 \end{cases}
\begin{cases} x(x - 2) \ge 0 \\ x^2 - 5x =0 \end{cases} \lor \begin{cases} x(x - 2) <0 \\ x^2 +x=0 \end{cases}
Notiamo che stesso discorso vale anche per le due equazioni, quindi mettiamo in evidenza anche lì una x:
\begin{cases} x(x - 2) \ge 0 \\ x(x - 5) =0 \end{cases} \lor \begin{cases} x(x - 2) <0 \\ x(x +1)=0 \end{cases}
Adesso concentriamoci su un sistema alla volta per non fare confusione! Partiamo dal PRIMO:
\begin{cases} x(x - 2) \ge 0 \\ x(x - 5) =0 \end{cases}
L’equazione x(x - 5) =0 ha come soluzione:
x=0 \lor x=5
per far sì che risulti =0.
Mentre per la disequazione dobbiamo andare a svolgere un falso sistema a parte (lo so che sono tanti passaggi ma bisogna farli):
\big\| x \ge 0 \\ \big\| x- 2 \ge 0
\big\| x \ge 0 \\ \big\| x \ge 2
Facciamo un quadro dei segni e andiamo a prendere gli intervalli col segno +, essendo la disequazione con un maggiore.
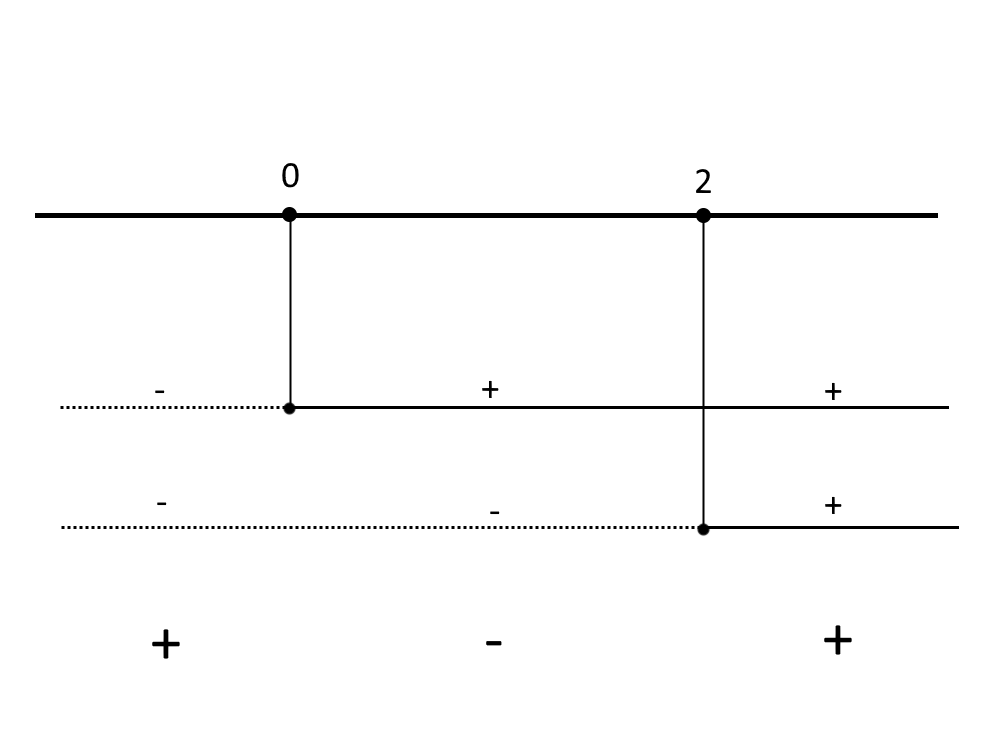
E quindi prendiamo:
x \le 0 \lor x \ge 2
E finalmente possiamo sostituire questi risultati nel primo sistema iniziale:
\begin{cases} x \le 0 \lor x \ge 2 \\ x=0 \lor x=5 \end{cases}
Notiamo che sia la soluzione x=0 sia la soluzione x=5 cadono negli intervalli pieni. Quindi sono entrambe soluzioni accettabili!
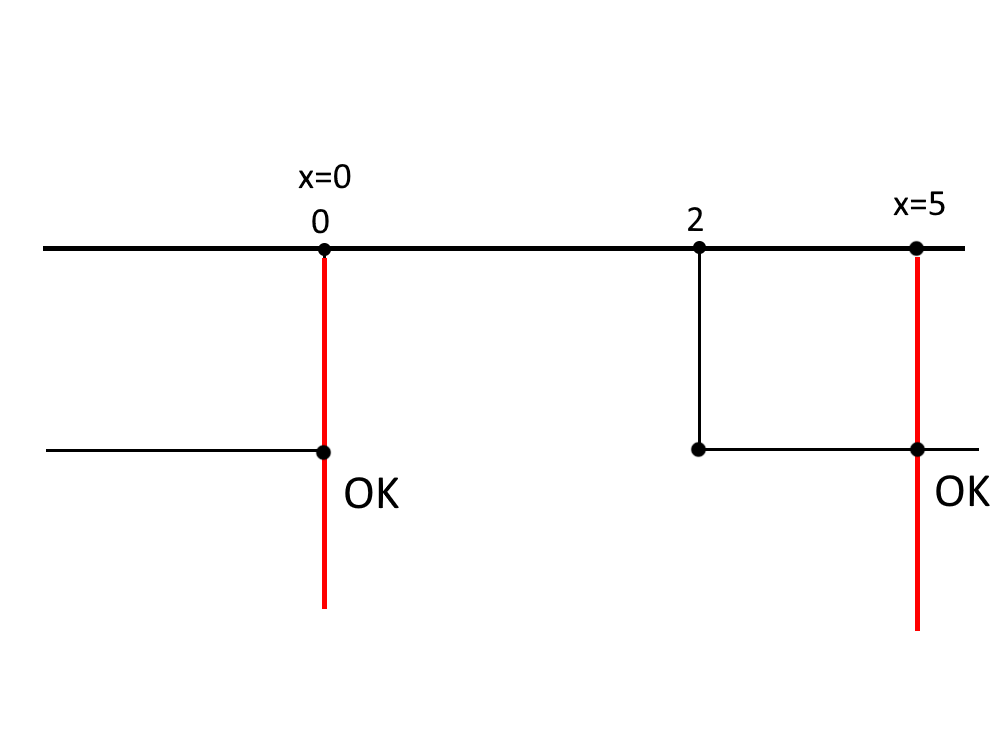
Adesso passiamo al SECONDO sistema:
\begin{cases} x(x - 2) <0 \\ x(x +1)=0 \end{cases}
L’equazione ha come soluzione x=0 e x=-1. Mentre per la disequazione dobbiamo risolvere un falso sistema:
\big\| x < 0 \\ \big\| x- 2 < 0
\big\| x < 0 \\ \big\| x < 2
Dove prendiamo gli intervalli col segno -, essendo la disequazione in questione con un minore (<) e quindi:
0<x<2
Sostituiamo nel sistema questi risultati:
\begin{cases} 0<x<2 \\ x=0 \lor x=-1 \end{cases}
E notiamo che nessuna delle due cade nell’intervallo 0<x<2. Quindi le uniche due soluzioni dell’esercizio che prendiamo sono quelle del primo sistema, ossia:
x=0, x=5
CON UN PASSAGGIO ALLA VOLTA SI FA TUTTO!
Esercizio 8. 2x - | 1 + x^2 | = 2
Iniziamo ad isolare come sempre il valore assoluto e poi a cambiare di segno arrivando a:
| 1 + x^2 | = 2x - 2
A questo punto siamo arrivati alla forma |f(x)|=g(x) e dobbiamo quindi per la risoluzione svolgere due sistemi:
\begin{cases} 1 + x^2 \ge 0 \\ 1 + x^2 = 2x - 2 \end{cases} \lor \begin{cases} 1 + x^2 <0 \\ 1 + x^2 = -2x + 2 \end{cases}
Partiamo con lo svolgere il primo sistema:
\begin{cases} 1 + x^2 \ge 0 \\ 1 + x^2 = 2x - 2 \end{cases}
Riordiniamo i vari termini.
\begin{cases} x^2 \ge -1 \\ x^2 -2x +3 = 0 \end{cases}
Il termine x^2 è un quadrato e quindi sempre maggiore di -1, ed allora scriviamo:
\begin{cases} \forall x \\ x^2 -2x +3 = 0 \end{cases}
L’equazione è di secondo grado, quindi andiamoci a calcolare il discriminante:
\frac{\Delta}{4} = (\frac{b}{2})^2 -ac = 1-3=-2<0
Il delta<0 e quindi non esiste soluzione.
\begin{cases} \forall x \\ \nexists x \end{cases}
E di conseguenza non esiste soluzione per questo sistema. Passiamo al secondo sistema:
\begin{cases} 1 + x^2 <0 \\ 1 + x^2 = -2x + 2 \end{cases}
Qui possiamo giocare d’astuzia e notare che per la disequazione abbiamo che:
x^2 < -1 \implies impossibile.
E visto che in un sistema bisogna prendere le soluzioni in comune, qualsiasi sia il risultato del secondo termine del sistema la soluzione sarà impossibile.
Quindi nessuno dei due sistemi ha soluzione.
Continuiamo con altri esercizi equazioni con valore assoluto!
Esercizi equazioni con valore assoluto della forma:
|f(x)| = |g(x)|
Esercizio 9. | 2x + 1 | = | 6-x |
Quando abbiamo due valori assoluti, questo significa che ciò che c’è all’interno o è uguale, o è opposto. Questo è il caso più semplice, perchè basterà risolvere le seguenti due equazioni separatamente:
f(x)=g(x)
f(x)=-g(x)
Tutto qui! Quindi in questo caso basterà risolvere queste due equazioni di primo grado:
2x + 1 = 6-x
2x + 1 = - ( 6-x )
In pratica una con un segno + ed una con un segno – ! Partiamo dalla prima equazione:
2x + 1 = 6-x
Chiaramente portiamo le x a primo membro, e i numeri al secondo, ricordandoci di cambiare segno quando passiamo da una parte all’altra.
2x + x = 6-1
3x = 5
E quindi la soluzione di questa prima equazione è:
x= \frac{5}{3}
Passiamo alla seconda equazione:
2x + 1 = - ( 6-x )
2x + 1 = - 6 +x
Facciamo stesso procedimento:
2x -x = - 6-1
x = -7
Le due soluzioni dell’esercizio sono allora:
x=-7 \lor x= \frac{5}{3}
Esercizio 10. | 5 - 16x | = | x |
Il procedimento è uguale, dobbiamo risolvere le seguenti due equazioni di primo grado separatamente:
5 - 16x = x
5 - 16x = - x
Partiamo dalla prima equazione portando le x a primo membro e il 5 a secondo, otteniamo:
- 16x -x = -5
- 17x = -5
Cambiamo di segno e dividiamo per 17, ed otteniamo la soluzione:
x = \frac{5}{17}
Passiamo alla seconda equazione facendo lo stesso procedimento:
- 16x +x = - 5
- 15x = - 5
E quindi:
x = \frac{1}{3}
Leggermente più lungo quando abbiamo a che fare con equazioni di secondo grado, come nel seguente esercizio.
Esercizio 11. | x^2 + 2x | = | x +20 |
Dobbiamo risolvere:
x^2 + 2x = x +20
x^2 + 2x = -( x +20)
Partiamo dalla prima equazione di secondo grado.
x^2 + 2x = x +20
Riordiniamola nella forma consueta per il calcolo del discrimiante.
x^2 + 2x-x -20 = 0
x^2 + x -20 = 0
A questo punto calcoliamo il delta:
\Delta = b^2 - 4ac = 1 + 80 = 81
E calcoliamo le due soluzioni distinte e separate, essendo il delta>0:
x_{1,2} = \frac{- b \pm \sqrt{\Delta} }{2a} = \frac{-1 \pm 9 }{2}
E quindi le due soluzioni per questa prima equazione sono:
x_1 = \frac{-1 + 9 }{2} = 4
x_2 = \frac{-1 - 9 }{2} = -5
Ora passiamo alla seconda equazione, anche questa di secondo grado:
x^2 + 2x = -( x +20)
x^2 + 2x = -x -20
Riordiniamola.
x^2 + 3x +20 = 0
E calcoliamone ora il delta:
\Delta = b^2 - 4ac = 9 -80 = -81 < 0
Il delta è negativo e quindi non esiste alcuna soluzione.
Esercizio 13. | x + 4 | = | \frac{7}{x-2} |
Qui dobbiamo andare a risolvere due equazioni fratte:
x + 4 = \frac{7}{x-2}
x + 4 = - \frac{7}{x-2}
Prima di iniziare, dobbiamo andare a scrivere le condizioni di esistenza, ossia denominatore diverso da zero, che in entrambe le equazione le CE sono le stesse.
CE: x-2 \ne 0 \implies x \ne 2
Ora possiamo passare ad iniziare a svolgere la prima.
x + 4 = \frac{7}{x-2}
Se non vi ricordate come si svolgono, cliccateci un attimo. Comunque il primo passaggio è fare il minimo comune multiplo ad ambo i membri:
\frac{(x + 4)(x-2)}{x-2} = \frac{7}{x-2}
Semplifichiamo i denominatori.
(x + 4)(x-2) = 7
E svolgiamo la parentesi:
x^2 -2x +4x -8= 7
x^2 +2x -15=0
Abbiamo una equazione di secondo grado: calcoliamo il discriminante, usando questa formula, essendo il coefficiente b pari.
\frac{\Delta}{4} = (\frac{b}{2})^2 -ac = 1+15=16
Delta>0 e ci aspettiamo due soluzioni distinte e separate:
x_{1,2} = \frac{- \frac{b}{2} \pm \sqrt{\frac{\Delta}{4}} }{a} = \frac{-1 \pm 4 }{1}
Le due soluzioni per questa prima equazione sono:
x_1 = -1+4 = 3
x_2 = -1-4 = -5
Passiamo alla secoda, equazione fratta.
x + 4 = - \frac{7}{x-2}
I passaggi sono gli stessi ma attenti al segno opposto! Facciamo il mcm:
\frac{(x + 4)(x-2)}{x-2} = \frac{-7}{x-2}
Semplifichiamo i denominatori ed otteniamo:
(x + 4)(x-2) = -7
Svogliamo la parentesi, copiamo lo stesso risultato di prima, non cambia nulla, solo il segno del 7.
x^2 -2x +4x -8= -7
x^2 +2x -1= 0
Abbiamo ottenuto ancora una volta una equazione di secondo grado, calcoliamone il delta:
\frac{\Delta}{4} = (\frac{b}{2})^2 -ac = 1+1=2
Ed andiamoci a calcolare finalmente le altre due soluzioni dell’esercizio:
x_{1,2} = \frac{- \frac{b}{2} \pm \sqrt{\frac{\Delta}{4}} }{a} = -1 \pm \sqrt{2}
Tutte e 4 le soluzioni ottenute rispettano le CE, e quindi non escludiamo nessuna!
Continuiamo con altri esercizi equazioni con valore assoluto!
Equazioni con valore assoluto con parametri
Esercizio 14. Calcola le soluzioni al variare del parametro reale h.
| 5x +h | = h+3
k è un numero, quindi ci troviamo di fronte al caso di una equazione con valore assoluto della prima forma:
|f(x)| = k
dove ricordiamo che se k<0, non c’è alcuna soluzione. Quindi nel nostro caso (dove k=h+3) se:
h+3<0 \implies h<-3
Non c’è alcuna soluzione. Ed abbiamo discusso così il primo caso. L’altro caso è che tutto il numero a secondo membro sia maggiore di zero, cioè nel nostro caso se:
h+3>0 \implies h>-3
E qui risolviamo l’equazione applicando la formula, quindi troviamo:
5x +h =\pm (h+3)
Quindi in questo caso, dobbiamo andare a risolvere due equazioni:
5x +h = h+3
5x +h =-( h+3 )
Partiamo dalla prima equazione, lasciando la h così com’è, trovando semplicemente la x.
5x = h-h+3
5x = 3 \implies \frac{3}{5}
Adesso passiamo alla seconda equazione, trovando un’altra soluzione ancora.
5x +h =-( h+3 )
5x +h =-h-3
E quindi:
5x =-2h-3
\implies x = \frac{-2h-3}{5}
Adesso abbiamo l’ultimo caso, ossia quando il secondo membro è uguale a zero, e quindi ciò significa che tutto ciò che c’è dentro al valore assoluto è nullo.
Se h+3=0 ossia h=-3 segue che:
| 5x -3 | = 0
E se il valore assoluto stesso è nullo implica che ciò che c’è dentro sia nullo:
5x - 3 = 0 \implies x = \frac{3}{5}
E la discussione è completa!
Esercizio 15. | kx - 2 | = k+1
Anche questo esercizio ha la stessa forma di equazione con valore assoluto di prima, quindi dobbiamo distinguere tre casi.
Se k+1 <0 \implies k < -1
Allora il secondo membro è negativo, e come abbiamo visto nel primo capitolo non ha soluzione questo caso, perchè un valore assoluto è per definizione positivo.
Invece se k+1 >0 \implies k > -1
Ciò implica che vi è soluzione, e quindi applicando la formula dobbiamo risolvere queste due equazioni:
kx - 2 = k+1
kx - 2 = -(k+1)
Partiamo dalla prima equazione. Stesso procedimento di prima.
kx - 2 = k+1
kx = k+1+2
E quindi:
x =\frac{ k+3}{k}
Passiamo alla seconda equazione:
kx - 2 = -(k+1)
kx - 2 = -k-1
Ed allora:
kx = -k+1
E la seconda soluzione è allora:
x = \frac{-k+1}{k}
Adesso passiamo all’ultimo caso, ossia per k+1=0, ossia k=-1. Abbiamo:
| -x - 2 | = 0
E se il valore assoluto è zero ciò implica che ciò che c’è dentro deve essere uguale a zero, cioè:
-x-2 = 0 \implies x = -2
E anche questa discussione è conclusa!
Abbiamo visto in questa pagina tantissime varietà di esercizi di equazioni con valore assoluto! Come detto esse comprendono assolutamente la conoscenza delle equazioni, equazioni di secondo grado, equazioni fratte e disequazioni di secondo grado.
Trovate altre centinaia di esercizi svolti sia di matematica che geometria analitica e geometria!
Per approfondire:
https://it.wikiversity.org/wiki/Equazione_con_il_valore_assoluto
disequazione
impossibile?
valore
assoluto