Equazioni Logaritmiche ESERCIZI
Equazioni Logaritmiche ESERCIZI: 15 esercizi SVOLTI! Per la verifica sulle equazioni logaritmiche basteranno un paio di giorni su questa pagina: a capire e risolvere insieme a noi gli esercizi sulle equazioni logaritmiche. Iniziamo subito!
Indice
- Proprietà dei logaritmi
- Equazioni logaritmiche \log_a b = c
- Equazioni logaritmiche \log_a b = \log_a c
- Equazioni logaritmiche con più logaritmi
- Equazioni logaritmiche con sostituzione
Per la risoluzione degli esercizi è importantissimo sapere le proprietà dei logaritmi: segnatevele su un foglio!
Proprietà dei logaritmi
Iniziamo subito con le equazioni logaritmiche esercizi svolti!
Equazioni logaritmiche esercizi
\log_a b = c
Esercizio 1. \ln ( x-2 ) = 1
Il PRIMO PUNTO fondamentale e da non saltare mai in nessuna equazione logaritmica è scrivere le condizioni d’esistenza: importantissime perchè ci diranno alla fine dell’esercizio se la soluzione trovata va bene o no! Per le funzioni logaritmiche le condizioni di esistenza significa scrivere l’argomento del/i logaritmo/i positivo.
CE: x-2 > 0 \implies x > 2
Le soluzioni che dovremmo prendere dovranno quindi essere maggiori di 2. Solo adesso possiamo procedere alla risoluzione dell’esercizio.
Quando abbiamo la forma di equazione seguente
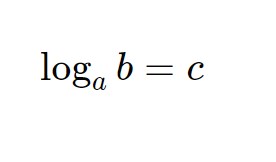
allora possiamo applicare la formula più importante per lo svolgimento degli esercizi di questo capitolo, ossia:
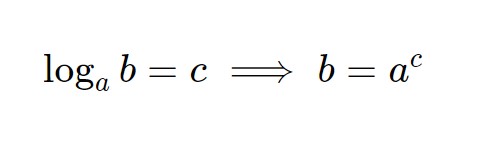
Cioè passiamo dal logaritmo all’esponenziale. Ricordando che il \ln significa logaritmo in base e, allora nel nostro caso applicando la formula otteniamo:
\ln ( x-2 ) = 1 \implies x-2=e^1
Ossia:
x-2 = e
Per cui grazie a questa importantissima formula siamo passati da logaritmi ad una equazione semplice che sappiamo risolvere! Di fatti portiamo il -2 a secondo membro (ricordatevi di cambiare segno quando passate da una parte all’altra) ed otteniamo:
x= e +2
Tale soluzione rispetta anche le CE e quindi va bene perchè è una soluzione più grande di 2 (come dicono le CE) quindi è ok. L’esercizio è concluso!
Volendo, durante la verifica in classe visto che non avete il risultato del libro, per vedere se avete commesso errori potete effettuare la verifica dell’equazione, per controllare se le soluzioni sono giuste.
Esercizio 2. \log_4 ( 3x-20 ) = 3
Vediamo un altro esercizio simile al precedente. Come primissima cosa non dimenticatevi mai le condizioni di esistenza, cioè argomento maggiore di zero, facciamole.
CE: 3x-20 > 0 \implies x > \frac{20}{3}
Anche questa equazione è della stessa forma di quella precedente, e quindi possiamo sempre applicare la formula solita di prima che ci permette di passare agli esponenziali.
\log_a b = c \implies b = a^c
Nel nostro caso:
\log_4 ( 3x-20 ) = 3 \implies 3x-20 = 4^3
Ed allora dovremmo solamente risolvere una equazione lineare:
3x-20 = 4^3
3x-20 = 64
Portiamo il -20 a secondo membro:
3x = 64+20
E poi dividiamo per 3. La soluzione è:
x = 28
La soluzione rispetta le CE, perchè x=28 è più grande di \frac{20}{3} = 6,66 ed allora va bene! (Ci saranno casi in cui la soluzione viene scartata per via delle CE).
Esercizio 3. \log_{ \frac{1}{3} } ( 2x-3 ) = -2
Qui abbiamo una piccola differenza, cioè la base del logaritmo è più piccola di 1, non cambia presso a poco nulla né nel procedimento né nella formula da usare. Partiamo dalle CE.
CE: 2x-3 >0 \implies x > \frac{3}{2}
Fatto ciò, abbiamo l’equazione logaritmica che è nella forma adatta per applicare la formula, quindi facciamolo!
\log_{ \frac{1}{3} } ( 2x-3 ) = -2 \implies 2x-3= (\frac{1}{3})^{-2}
L’equazione seguente, ossia:
2x-3= (\frac{1}{3})^{-2}
è facilmente risolvibile ricordando la quarta proprietà delle potenze, di conseguenza possiamo scrivere quel termine esponenziale come:
2x-3= 3^2
2x-3= 9
Arriviamo alla soluzione dell’esercizio:
x= 6
Che rispetta le condizioni d’esistenza e quindi ce la prendiamo. Non dimenticatevi mai di controllare le CE!
Continuiamo con altre equazioni logaritmiche esercizi!
Equazioni logaritmiche esercizi
\log_a b = \log_a c
Esercizio 4. \log ( x-2 ) = \log (2x +3 )
Adesso vediamo invece il caso in cui abbiamo una equazione logaritmica in cui abbiamo due logaritmi con stessa base.
Prima di spiegarvi come si procede, la prima cosa da fare anche in questo caso è scrivere le condizioni di esistenza, che questa volta ne sono due! Quando ne sono più di una bisogna scrivere un sistema e prendere le soluzioni comuni, per ottenere così una unica condizione d’esistenza. Poniamo quindi entrambi gli argomenti positivi:
CE: \begin{cases} x-2 > 0 \\ 2x+3 > 0 \end{cases}
CE: \begin{cases} x > 2 \\ x > - \frac{3}{2} \end{cases}
E visto che è un sistema, bisogna prendere gli intervalli di soluzione in comune!
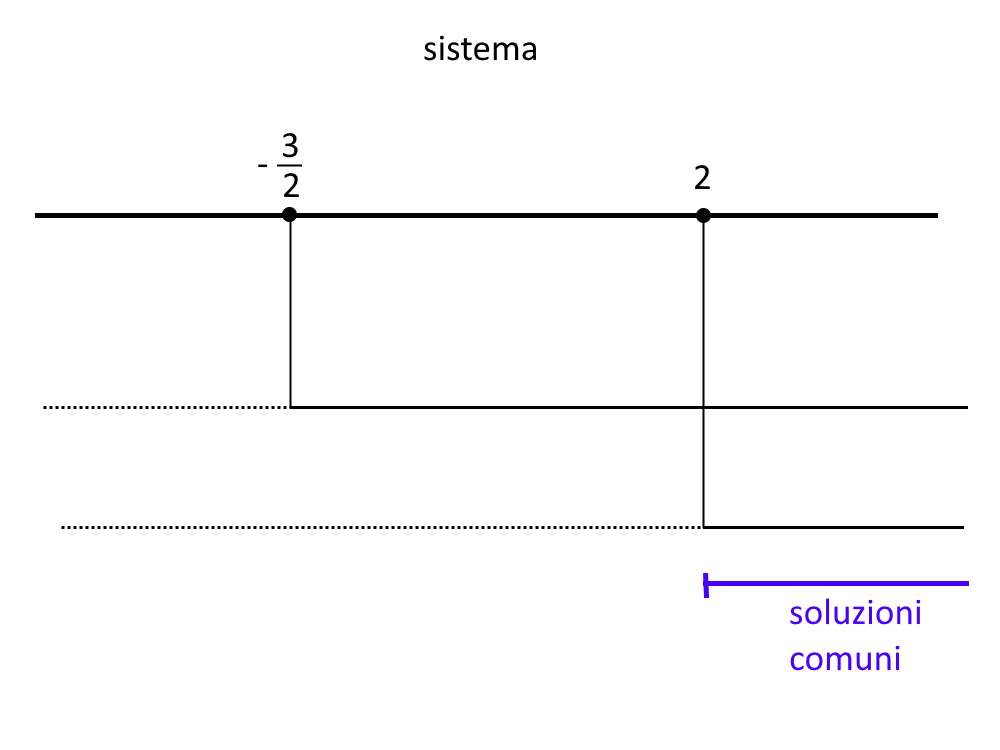
Quindi:
CE: x>2
Adesso possiamo passare alla risoluzione vera e propria dell’esercizio. Se abbiamo esattamente le stesse basi, senza coefficienti davanti ai logaritmi, allora si può applicare la nuova formula seguente che applicheremo anche dopo.
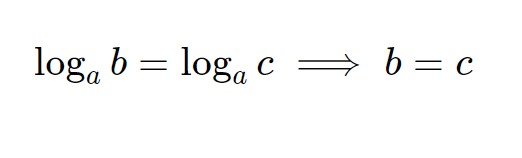
Quindi basterà uguagliare gli argomenti dei due logaritmi!
x-2 = 2x +3
Risolviamo questa equazione!
x-2x = 2 +3
-x = 5
Cambiamo tutto di segno ed otteniamo:
x=-5
Questa soluzione però non rispetta le CE! Quindi la scartiamo, non va bene!
Diciamo allora che tale equazione non ha soluzione o è impossibile.
Esercizio 5. 2 \log_5 x = \log_5 (2x-1)
Calcoliamo un attimo le CE.
CE: \begin{cases} x > 0 \\ 2x-1 > 0 \end{cases}
CE: \begin{cases} x > 0 \\ x > \frac{1}{2} \end{cases}
E quindi prendiamo l’intervallo comune di:
CE: x > \frac{1}{2}
Ora possiamo procedere.
Qui abbiamo sicuramente due logaritmi con stessa base, ma c’è un coefficiente 2 prima di un logaritmo, e la formula dice che ci devono essere solo logaritmi senza nient’altro! Quindi quello che facciamo per levare questo 2 di mezzo è applicare la terza proprietà dei logaritmi. Ossia:
\log_a b^n = n \cdotp \log_a b
Quindi nel nostro caso viene:
\log_5 x^2 = \log_5 (2x-1)
Attenzione a non confondervi! Il 2 va ad elevare solamente l’argomento del logaritmo non tutto il logaritmo! Cioè:
2 \log_5 x \implies \log_5 x^2
E NON:
2 \log_5 x \implies \log_5 ^2 x
Torniamo alla nostra equazione:
\log_5 x^2 = \log_5 (2x-1)
Essa ora ha la forma giusta per applicare la formula: uguagliamo gli argomenti.
x^2 = 2x-1
x^2 - 2x+1 = 0
Qui abbiamo una equazione di secondo grado, quindi calcoliamo il Delta-quarti, visto che il secondo termine è pari (se non ricordate queste cose cliccateci un attimo e segnatevele che vi serviranno).
\frac{\Delta}{4} = ( \frac{b}{2} )^2 -ac = 1-1 = 0
Il discriminante è zero, e quindi abbiamo una soluzione. Calcoliamola con la formula:
x = \frac{- \frac{b}{2} \pm \sqrt{\frac{\Delta}{4}} }{a} = 1 \pm 0 = 1
Essa rispetta le CE, quindi è ok.
Come potete vedere vecchi argomenti come le equazioni di secondo grado ritornano, ma torneranno anche altri.
Esercizio 6. \log_2 x = \log_{ \frac{1}{2} } (2x-1)
CE: \begin{cases} x > 0 \\ 2x-1 > 0 \end{cases}
CE: \begin{cases} x > 0 \\ x > \frac{1}{2} \end{cases}
E quindi prendiamo CE: x > \frac{1}{2}
Torniamo all’equazione: essa ha due logaritmi e ciò va bene, ma con basi diverse. Quindi ciò che dobbiamo fare è applicare la formula del cambiamento di base:
\log_a b = \frac{\log_c b }{\log_c a}
Nel nostro caso il termine:
\log_c b = \log_2 x
Visto che vogliamo la base in 1/2, allora moltiplichiamo e dividiamo per:
\log_2 x \frac{ \log_2 \frac{1}{2} }{ \log_2 \frac{1}{2} } = \log_{ \frac{1}{2} } (2x-1)
\log_2 \frac{1}{2} \frac{ \log_2 x }{ \log_2 \frac{1}{2} } = \log_{ \frac{1}{2} } (2x-1)
Il termine in frazione sarebbe il logaritmo nella nuova base, quindi l’equazione diventa:
\log_2 \frac{1}{2} \cdotp \log_{ \frac{1}{2} } x = \log_{ \frac{1}{2} } (2x-1)
Ora dobbiamo solo levare di mezzo il primo pezzo. Adesso vediamo sempre in tabella ed anche usando le proprietà delle potenze, riscriviamo il primo pezzo come:
\log_2 \frac{1}{2} = \log_2 (2)^{-1} = -1 \cdotp \log_2 2 = -1 \cdotp 1 = -1
E quindi sostituendo nell’equazione si ha:
-1 \cdotp \log_{ \frac{1}{2} } x = \log_{ \frac{1}{2} } (2x-1)
Non abbiamo però ancora l’esatta forma per applicare la formula, perchè dobbiamo avere due logaritmi senza nient’altro. Applichiamo sempre la terza proprietà dei logaritmi, e quindi il – va ad elevare la x:
\log_{ \frac{1}{2} } x^{-1} = \log_{ \frac{1}{2} } (2x-1)
Che sarebbe una frazione!
\log_{ \frac{1}{2} } \frac{1}{x} = \log_{ \frac{1}{2} } (2x-1)
Adesso applichiamo la formula e quindi eguagliamo gli argomenti dei logaritmi:
\frac{1}{x} = 2x-1
Abbiamo adesso una equazione fratta da risolvere. Come vedete nei passaggi finali ritornano argomenti passati, quindi cliccateci sopra e scrivete un attimo i passaggi da seguire per risolverla.
Prima di tutto anche qui CE, che significa denominatore diverso da zero.
CE: x\ne 0
Che unita all’iniziale CE non cambia nulla, e quindi sempre x > \frac{1}{2} rimane.
Adesso o facciamo il minimo comune multiplo, o moltiplichiamo tutto per x. Moltiplichiamo tutto per x che è più veloce:
1 = 2x^2 - x
Riordiniamola:
2x^2 - x -1 = 0
Abbiamo una equazione di secondo grado, quindi calcoliamo il Delta:
\Delta = b^2 - 4ac = 1 +8 = 9
Delta>0 e quindi esistono due soluzioni: andiamo a calcolarle!
x_{1,2} = \frac{- b \pm \sqrt{ \Delta } }{2a} = \frac{1 \pm 3}{4}
E quindi le due soluzioni sono:
x_1 = \frac{1 + 3}{4} =1
x_2 = \frac{1 - 3}{4} = - \frac{1}{2}
A causa delle CE, solo la prima soluzione prendiamo. Quindi l’unica soluzione è: x=1.
Continuiamo con altre equazioni logaritmiche esercizi!
Equazioni logaritmiche esercizi con più logaritmi
Esercizio 9. \log_5 x + \log_5 3 = \log_5 6
Prima di iniziare partiamo con le condizioni di esistenza anche qui.
CE: x>0
Ora possiamo cominciare. Quando avete più di due logaritmi bisogna sempre fare una cosa: o applichiamo la prima proprietà dei logaritmi o la seconda! Questo per far sì di ridurre il numero di logaritmi.
In questo caso notiamo che abbiamo un solo logaritmo a destra e questo ci va bene. Se applichiamo la prima proprietà al primo membro arriveremo ad avere un logaritmo a sinistra ed uno a destra e siamo ritornati al caso precedente!
Sfruttiamo quindi:
\log_a b + \log_a c = \log_a b\cdotp c
Nel nostro caso ai primi due termini:
\log_5 3x = \log_5 6
E siamo arrivati esattamente al caso di prima! Quindi da qui in poi è uguale: uguagliamo gli argomenti!
3x = 6 \implies x =2
Che rispettano anche le CE.
Esercizio 10. \log_3 5 + \log_3 2 - \log_3 x = \log_3 4
CE: x>0
(le CE si fanno solo con gli argomenti che presentano una x ovviamente)
Allora l’obiettivo è ridurre il numero di logaritmi, quindi ai primi due termini applichiamo la prima proprietà:
\log_3 5\cdotp 2 - \log_3 x = \log_3 4
\log_3 10 - \log_3 x = \log_3 4
Dobbiamo ridurre ulteriormente, adesso applichiamo ai primi due termini la seconda proprietà perché abbiamo un segno meno (-).
\log_3 \frac{10}{x} = \log_3 4
Ed adesso possiamo uguagliare gli argomenti:
\frac{10}{x} = 4
Abbiamo una equazione fratta, quindi poniamo denominatore diverso da zero.
CE: x \ne 0
Moltiplichiamo tutto per x:
10 = 4x \implies x = \frac{5}{2}
Che rispetta anche le CE.
Esercizio 11. \log x - \log 4 = \log (x-1) + \log 3
CE: x-1>0 \implies x > 1
CE:x>0
E quindi possiamo scrivere un’unica condizione d’esistenza come x>1.
Qui abbiamo 4 logaritmi, 2 a sinistra e 2 a destra. Applichiamo allora la prima proprietà dei logaritmi a secondo membro visto che abbiamo una somma, e la seconda proprietà al primo membro visto che abbiamo una differenza. Così otteniamo:
\log \frac{x}{4} = \log 3(x-1)
I logaritmi hanno stessa base e ne abbiamo solo due, quindi possiamo uguagliare i loro argomenti, arrivando così alla soluzione dell’esercizio.
\frac{x}{4} = 3(x-1)
Moltiplichiamo tutto per 4 per levare di mezzo quella frazione:
x= 12(x-1)
x= 12x-12
Portiamo le x a primo membro:
x- 12x = -12
-11x = -12
Cambiamo tutto di segno e dividiamo per 11, per isolare la x.
x = \frac{12}{11}
Esercizio 12. \log_2 (x^2 - 4 ) + 2 \log_2 x = 1 + \log_2 (5x^2 +16)
Prima della discussione, facciamo un secondo le tre condizioni d’esistenza.
CE: x^2 -4 > 0 \implies x^2 > 4
\implies x<-2 \lor x > 2
Facciamo la seconda: x>0
E l’ultima:
CE: 5x^2 + 16 > 0 \implies 5x^2 > -16
\implies \forall x essendo un quadrato sempre positivo.
Riassumendole, abbiamo solo che x>2.
Passiamo alla discussione. Così d’occhio c’è un 1 che dà fastidio. Ma così come l’1 era un jolly nelle equazioni esponenziali, così è un jolly anche qui. E’ possibile trasformare di fatti un numero in logaritmo.
Di fatti vedendo nella tabella in basso, visto che in questo esercizio ci serve un logaritmo in base 2, allora possiamo scrivere quell’1 come:
1= \log_2 2
Sostituiamo:
\log_2 (x^2 - 4 ) + 2 \log_2 x = \log_2 2 + \log_2 (5x^2 +16)
Ora al secondo termine c’è un coefficiente moltiplicativo 2 davanti al logaritmo e quindi applichiamo la terza proprietà per levarcelo da mezzo.
\log_2 (x^2 - 4 ) + \log_2 x^2 = \log_2 2 + \log_2 (5x^2 +16)
Ora abbiamo tutti e soli logaritmi in stessa base, possiamo quindi applicare la prima proprietà per ridurre il numero.
\log_2 x^2(x^2 - 4 ) = \log_2 2(5x^2 +16)
Uguagliamo gli argomenti:
x^2(x^2 - 4 ) = 2(5x^2 +16)
Sciogliamo le parentesi:
x^4 - 4x^2 = 10x^2 + 32
Portiamo tutto a primo membro:
x^4 - 14x^2 -32 = 0
Abbiamo di fronte una equazione di quarto grado, che però abbiamo già visto negli esercizi sulle equazioni di secondo grado. Di fatti queste si risolvono per sostituzione. Cioè poniamo:
z=x^2
E l’equazione diventa proprio di secondo grado:
z^2 - 14z -32 = 0
Calcoliamo il discriminante:
\frac{\Delta}{4} = ( \frac{b}{2} )^2 -ac = 49+32 = 81
Delta-quarti > 0 e quindi esistono due soluzioni. Calcoliamole:
z_{1,2} = \frac{- \frac{b}{2} \pm \sqrt{\frac{\Delta}{4}} }{a} = 7 \pm 9
Abbiamo:
z_1 = 7+9 = 16
z_2 = 7-9 = -2
Attenzione perchè queste sono le soluzioni nelle variabili z. L’esercizio le vuole in x, quindi risostituiamo uno alla volta, partiamo dal secondo:
z= x^2 = -2
Essendo un quadrato per definizione maggiore o uguale a zero, esso non può mai essere uguale a -2, quindi qui non c’è soluzione. Andiamo all’altro:
z= x^2 = 16 \implies x = \pm 4
Dove però viste le CE, ci teniamo solamente x=4!
Continuiamo con altre equazioni logaritmiche esercizi!
Equazioni logaritmiche esercizi con sostituzione
Esercizio 13. 3 \log^2 x - 2 \log x = 0
CE: x>0
Quando abbiamo a che fare con logaritmi elevati a qualcosa ( che è ben diverso dalla terza proprietà ) come:
\log^2 x
Allora solitamente si svolge l’esercizio utilizzando una sostituzione. Poniamo:
\log x = t
E quindi l’equazione nella nuova variabile diventa:
3 t^2 - 2 t = 0
Ossia una equazione di secondo grado. Per applicare questo metodo c’è bisogno di due cose: sia la base che gli argomenti dei logaritmi devono essere uguali.
Mettiamo in evidenza la t:
t( 3t - 2 ) = 0
E quindi le due soluzioni in t sono:
t=0 \lor 3t -2 = 0
Ossia.
t=0 \lor t = \frac{2}{3}
Per concludere l’esercizio, come sempre quando si effettua una sostituzione, bisogna tornare alla variabile iniziale x.
Partiamo da t=0 e risostituiamo.
\log x = t = 0 \implies \log x = 0
Questa è una equazione fatta nel primo caso, ad inizio pagina. Quindi sfruttiamo la formula che ci permette di passare dai logaritmi agli esponenziali.
\log x = 0 \implies x = 10^0 = 1
Passiamo ora alla seconda soluzione.
\log x = \frac{2}{3} \implies x = \sqrt[3]{10^2}
Ed abbiamo anche la seconda soluzione, entrambe per le CE vanno bene.
Esercizio 14. \log_4 ^2 x + 3 \log_4 x = 4
CE: x>0
Qui abbiamo un logaritmo al quadrato ( quindi subito ci deve venire in mente di fare una sostituzione ), inoltre i logaritmi che ci sono hanno stessa base e stesso argomento. Quindi poniamo:
\log_4 x = t
Abbiamo ora:
t^2 + 3t = 4
t^2 + 3t - 4 = 0
Equazione di secondo grado: calcoliamo il discriminante o delta (sono sinonimi).
\Delta = b^2 - 4ac = 9 + 16 = 25
Delta>0 quindi esistono due soluzioni nella variabile t. Troviamole con la formula:
t_{1,2} = \frac{- b \pm \sqrt{ \Delta } }{2a} = \frac{-3 \pm 5}{2}
E quindi:
t_1 = \frac{-3 + 5}{2} = 1
t_2 = \frac{-3 - 5}{2} = -4
Abbiamo le due soluzioni in t, ora ritorniamo alle x. partiamo dalla prima t=1, ed applichiamo sempre la formula per passare dal logaritmo all’esponenziale.
\log_4 x = 1 \implies x=4^1=4
Trovata la prima, passiamo all’altra:
\log_4 x = -4 \implies x=4^{-4}=\frac{1}{256}
Prendiamo entrambe perché rispettano le CE.
Esercizio 15. \log_2 ^2 x^2 + 4 \log_2 \sqrt{x} -2 = 0
CE: x^2 > 0 \implies x >0
Per la radice è equivalente:
CE: \sqrt{x} > 0 \implies x >0
Qui l’idea che ci balza alla mente è la sostituzione però: abbiamo sì stesse basi, ma con argomenti diversi. Quindi riscriviamo la radice come:
\log_2 ^2 x^2 + 4 \log_2 x^{\frac{1}{2}} -2 = 0
E poi usando la terza proprietà portiamo gli esponenti degli argomenti fuori dai logaritmi.
\log_2 ^2 x^2 + 4\frac{1}{2} \log_2 x -2 = 0
\log_2 ^2 x^2 + 2 \log_2 x -2 = 0
Sul primo c’è da stare molto attenti! Prendiamolo da parte e guardiamo:
\log_2 ^2 x^2 = (\log_2 x^2 )^2 = (2 \log_2 x )^2 =
= 4 \log_2 ^2 x
Quindi come vedete non è solo portare il 2 fuori, perchè essendo un logaritmo quadro, il 2 diventa 4 perchè si eleva anch’esso!
4 \log_2 ^2 x + 2 \log_2 x -2 = 0
Dividiamo inoltre tutto per 2 per comodità.
2\log_2 ^2 x + \log_2 x -1 = 0
Ed ora siamo nelle condizioni per fare una sostituzione. Poniamo:
\log_2 x = t
L’equazione diventa:
2t^2 + t -1 = 0
Ossia una equazione di secondo grado, calcoliamo il discriminante.
\Delta = b^2 - 4ac = 1 + 8 = 9
Troviamo le due soluzioni in t:
t_{1,2} = \frac{- b \pm \sqrt{ \Delta } }{2a} = \frac{-1 \pm 3}{4}
E così:
t_1 = \frac{-1 + 3}{4} = \frac{1}{2}
t_2 = \frac{-1 - 3}{4} = -1
Ritorniamo alla variabile iniziale. Partiamo dalla seconda soluzione.
\log_2 x = -1 \implies x= 2^{-1} = \frac{1}{2}
E poi all’altra.
\log_2 x = -1 \implies x= 2^{\frac{1}{2}} =\sqrt{2}
Entrambe rispettano le CE, quindi non le scartiamo!
Abbiamo concluso questa pagina contente 15 esercizi sulle equazioni logaritmiche. Ci sono servite anche le formule delle equazioni di secondo grado, equazioni fratte ed alcune proprietà usate nelle equazioni esponenziali.
Trovate altre centinaia di esercizi su questo sito sia di matematica che altro ancora!
Per approfondire:
https://it.wikipedia.org/wiki/Equazione_logaritmica
Equazioni logaritmiche esercizi.
numero in
logaritmo
logaritmiche
esercizi
