Equazioni di secondo grado: 20 esercizi SVOLTI
Equazioni di secondo grado: 20 esercizi SVOLTI! Le equazioni di secondo grado sono importantissime non solo per la verifica in classe, ma anche perchè le continuerete ad incontrare negli altri anni di Liceo! In questa pagina faremo vedere come si svolgono le equazioni di secondo grado, e le formule da memorizzare ed utilizzare! Iniziamo subito con l’indice che suddivide i vari sottoargomenti. Chiaramente prima di iniziare è importante che sappiate come si risolve una equazione.
Indice
- Formule per le equazioni di secondo grado
- Esercizi svolti equazioni di secondo grado
- Equazioni di secondo grado con parametri
- Equazioni di secondo grado per sostituzione
Iniziamo subito con questa tabella riassuntiva con le formule che servono per la risoluzione delle equazioni di secondo grado!
Formule per le equazioni di secondo grado
Iniziamo subito con le equazioni di secondo grado: esercizi svolti!
Esercizi svolti equazioni di secondo grado
Esercizio 1. x^2 -5x +6=0
L’equazione, come possiamo vedere, è già della forma della formula:
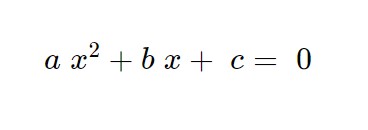
Il coefficiente b è dispari, quindi come prima cosa andiamo a calcolare prima di tutto il discriminante \Delta.
\Delta = b^2 - 4ac = 25-4\cdotp 6 \cdotp 1 = 25-24 = 1
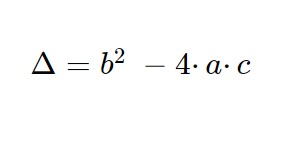
Quindi \Delta >0 e quando il discriminante è positivo allora esistono 2 soluzioni!
Applichiamo la formula generale per calcolare le soluzioni dell’equazione!
x_{1,2}= \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{5 \pm 1}{2}
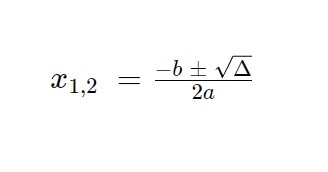
Ed ora abbiamo le due soluzioni dell’equazione:
x_1 = \frac{5+1}{2} = 3
x_1 = \frac{5-1}{2} = 2
Ed abbiamo concluso l’esercizio!
Volendo, durante la verifica in classe, per vedere se avete commesso errori potete effettuare la verifica dell’equazione, per controllare se le soluzioni sono giuste.
Esercizio 2. 4x^2 -7x +3=0
L’equazione è già della forma della formula, non dobbiamo fare nulla. Primo punto: calcolare il discriminante!
Notiamo che il coefficiente b è dispari quindi applichiamo per il calcolo del discriminante, la stessa formula di prima.
\Delta = b^2 - 4ac = 49-4\cdotp 4 \cdotp 3 = 49-48 = 1
Anche qui, il Delta (o discriminante, sono sinonimi) è positivo, quindi esisteranno 2 soluzioni, andiamocele a calcolare! Utilizziamo la solita formula che serve per la risoluzione di una equazione di secondo grado:
x_{1,2}= \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{7 \pm 1}{8}
E quindi le due soluzioni distinte e separate (perchè diverse) sono:
x_1 = \frac{7 + 1}{8} = 1
x_2 = \frac{7 - 1}{8} = \frac{6}{8}= \frac{3}{4}
Esercizio 3. -3x^2 -x +2=0
Qui abbiamo l’equazione con il coefficiente a della solita formula che è negativo. In questi casi vi consiglio fortemente di cambiare tutto di segno, in modo da non confondervi con i segni nell’utilizzo poi della formula!
3x^2 +x -2=0
Ora, come prima, abbiamo l’equazione nella forma giusta, possiamo andare a calcolare il Delta!
\Delta = b^2 - 4ac = 1-4\cdotp 3 \cdotp (-2) = 1+24= 25
Il Delta è positivo, quindi ci aspettiamo 2 soluzioni distinte ed infatti applichiamo la formula:
x_{1,2}= \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{-1 \pm \sqrt{25}}{6}=\frac{-1 \pm 5}{6}
L’esercizio sarà concluso calcolandoci:
x_1 = \frac{-1 + 5}{6} = \frac{4}{6}= \frac{2}{3}
x_2 = \frac{-1 - 5}{6} =- \frac{6}{6}=-1
Continuiamo con altre equazioni di secondo grado con esercizi svolti!
Esercizio 4. x^2 +6x +8=0
Qui l’equazione è della forma giusta, adesso però abbiamo il coefficiente b che è pari, quindi andiamo a calcolarci il discriminante con la formula seguente.
\frac{\Delta}{4} = (\frac{b}{2})^2 - ac = (3)^2 - 9 = 9-8= 1
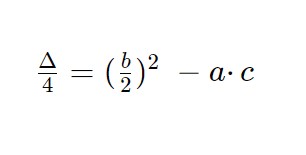
Il discriminante è positivo, ci aspettiamo 2 soluzioni distinte. Calcoliamole ora con la seguente formula:
x_{1,2}= \frac{-\frac{b}{2} \pm \sqrt{\frac{\Delta}{4}} }{a} = \frac{-3 \pm 1 }{1}
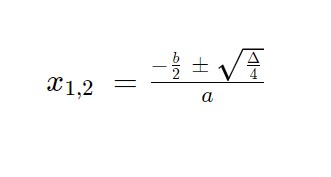
Le due soluzioni dell’esercizio sono quindi:
x_1 = -3+1 = -2
x_2 = -3-1 = -4
Esercizio 5. -x^2 +2x -2 =0
Abbiamo il coefficiente a negativo, quindi cambiamo prima di tutto di segno l’equazione! Dobbiamo semplificarci la vita!
x^2 -2x +2 =0
Ricordiamo che questo lo si può fare perchè stiamo moltiplicando per -1 entrambi i membri, e questo è il risultato.
Ora calcoliamo il discriminante, utilizzando la formula del \frac{\Delta}{4} poichè il coefficiente b è pari.
\frac{\Delta}{4} = (\frac{b}{2})^2 - ac = 1-2= -1
Abbiamo ora un discriminante negativo \frac{\Delta}{4} <0 e quindi non c’è soluzione!
Esercizio 6. (2-3x)x = \frac{1}{3}
Abbiamo questa volta una equazione non è immediatamente riconducibile alla forma solita:
ax^2 +bx + c=0
Quindi, iniziamo a svolgere la moltiplicazione con la parentesi.
2x - 3x^2 = \frac{1}{3}
Adesso portiamo \frac{1}{3} a primo membro, chiaramente ricordandoci di cambiare di segno, perchè quando si porta qualche termine da una parte o dall’altra si deve cambiare quel termine di segno.
2x - 3x^2 - \frac{1}{3} =0
Mettiamo in ordine i vari coefficienti:
- 3x^2 +2x - \frac{1}{3} =0
Abbiamo il coefficiente a negativo, quindi cambiamo ora tutta l’equazione di segno!
3x^2 -2x + \frac{1}{3} =0
Adesso possiamo finalmente calcolare il Delta.
\Delta = b^2 - 4ac = 4 - 4 \cdotp 3 \cdotp \frac{1}{3} = 4-4 =0
Il discriminante è uguale a zero, questo significa che esisteranno due soluzioni ma coincidenti! Ossia una soluzione:
x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{2}{6}=\frac{1}{3}
Continuiamo con altre equazioni di secondo grado con esercizi svolti!
Esercizio 7. \frac{ x^2}{2} -\sqrt{2 } x -8=0
Anche se a prima vista potrebbe sembrare una forma strana, l’equazione è esattamente della forma:
ax^2 +bx + c=0
Se non siete convinti ragionateci e notate che abbiamo:
a=\frac{1}{2} , b= - \sqrt{2} , c=-8
Se non siete convinti del coefficiente a, beh l’equazione la possiamo anche scrivere come:
\frac{ 1}{2}x^2 -\sqrt{2 } x -8=0
Adesso quindi, passiamo al calcolo del discriminante. Quando non sapete se il coefficiente è pari o dispari, utilizzate la formula di quello dispari!
\Delta = b^2 - 4ac = (-\sqrt{2})^2 + 4 \cdotp \frac{ 1}{2} \cdotp 8 = 2+16=18
Delta positivo, ci aspettiamo quindi 2 soluzioni distinte:
x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{\sqrt{2 } \pm \sqrt{18}}{2 \frac{1}{2}}=
= \frac{\sqrt{2 } \pm \sqrt{9 \cdotp 2}}{1}= \sqrt{2 } \pm 3 \sqrt{ 2}
Quindi le due soluzioni sono:
x_1 = \sqrt{2 } + 3 \sqrt{ 2} = 4 \sqrt{ 2}
x_2 = \sqrt{2 } - 3 \sqrt{ 2} = -2 \sqrt{ 2}
Esercizio 8. (3-2x)^2 - (2-x)^2 =0
Innanzitutto svolgiamo i due quadrati, usando la formula del quadrato di un binomio:
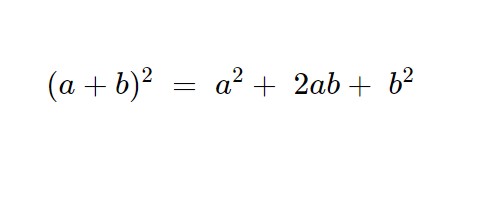
Quindi abbiamo che:
(9+4x^2 -12x) - (4+x^2 -4x ) =0
Sciogliamo le parentesi, stando attenti a quel segno meno davanti alla seconda parentesi che ne cambia tutto il segno!
9+4x^2 -12x - 4-x^2 +4x =0
Riordiniamo i termini:
4x^2 -x^2 -12x +4x -4+9 =0
E poi sommiamo i termini con stesso grado:
3x^2 -8x +5 =0
E adesso, possiamo finalmente calcolare il discriminante:
\frac{\Delta}{4} = (\frac{b}{2})^2 - ac = 16 - 15= 1
Adesso calcoliamo le due soluzioni:
x_{1,2}= \frac{-\frac{b}{2} \pm \sqrt{\frac{\Delta}{4}} }{a} = \frac{4 \pm 1 }{3}
E quindi abbiamo:
x_1 = \frac{4 + 1 }{3} = \frac{5}{3}
x_2 = \frac{4 - 1 }{3} = 1
Esercizio 9. \sqrt{3}x (\sqrt{3}x -2 ) =-1
Innanzitutto svolgiamo la moltiplicazione, sciogliendo quindi la parentesi:
\sqrt{3} \cdotp \sqrt{3}x -2\sqrt{3} =-1
3x^2 -2\sqrt{3}x =-1
E portiamo il -1 a primo membro.
3x^2 -2\sqrt{3}x +1 =0
Calcoliamo il Delta, quello riguardo l’dispari, essendoci una radice:
\Delta = b^2 - 4ac = (-2\sqrt{3})^2 - 4 \cdotp 3 = 12 -12=0
Abbiamo un discriminante uguale a zero, quindi ci aspettiamo due soluzioni coincidenti. Calcoliamole:
x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{2\sqrt{3}}{6}=\frac{\sqrt{3}}{3}
Ed il gioco è fatto!
Esercizio 10. \frac{x}{9} = (\frac{x-6}{3})^2
Iniziamo a svolgere chiaramente il quadrato. Se avete dubbi su come svolgerlo, scriviamola nella seguente forma equivalente più comoda:
\frac{x}{9} = \frac{(x-6)^2}{3^2}
Ed ora appare molto più familiare il quadrato di un binomio. Utilizziamo la formula usata anche negli esercizi predenti:
(a+b)^2 = a^2 + b^2 + 2ab
\frac{x}{9} = \frac{x^2 +36 - 12x }{9}
Ciò che notiamo adesso è che entrambi i membri hanno come denominatore il 9, quindi moltiplichiamo tutto per 9, così ci leviamo da mezzo la frazione e ci semplifichiamo l’esercizio!
9 \frac{x}{9} =9 \frac{x^2 +36 - 12x }{9}
x = x^2 +36 - 12x
Adesso portiamo tutto a primo membro (ricordatevi di cambiare segno quando passate dall’altro lato):
x -x^2 -36 +12x = 0
Ora sommiamo i termini con la x.
-x^2 -36 +13x = 0
-x^2 +13x -36 = 0
Ora abbiamo, come potete vedere, il coefficiente a negativo, quindi per comodità di calcolo andiamo a cambiare tutto di segno:
x^2 -13x +36 = 0
Ora possiamo finalmente calcolare il discriminante dell’equazione:
\Delta = b^2 - 4ac = 169 -144 = 25
Adesso possiamo usare la solita formula per l’equazione di secondo grado, e calcolarci le due soluzioni:
x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{13 \pm 5 }{2}
E quindi le due dell’esercizio soluzioni sono:
x_1 = \frac{13 + 5 }{2} = 9
x_2 = \frac{13 - 5 }{2} =4
Continuiamo con altre equazioni di secondo grado con esercizi svolti!
Esercizio 11. 0,75 x^2 + 0,5 x-2 =0
Anche se in questa equazione abbiamo dei numeri decimali, con la virgola, il processo è sempre lo stesso, non cambia nulla. L’equazione è nella forma classica, quindi andiamo a calcolare subito il discriminante:
\Delta = b^2 - 4ac = 0,25 + 6 = 6,25
Discriminante >0, ci aspettiamo due soluzioni distinte: calcoliamole!
x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{-0,5 \pm 2,5 }{1,5}
Quindi abbiamo:
x_1 = \frac{-0,5 + 2,5 }{1,5} = \frac{2}{1,5}
Se semplifichiamo dividendo per 0,5 otteniamo:
= \frac{4}{3}
x_2 = \frac{-0,5 - 2,5 }{1,5} =- \frac{3}{1,5} = -2
Esercizio 12. -x^2 +6(x-2) =0
Cosa fare come prima cosa? Ditelo voi…esatto, svolgiamo innanzitutto la parentesi:
-x^2 +6x-12 =0
Abbiamo il termine di x^2 negativo, quindi come detto tante volte, cambiamo tutto di segno per comodità. Così facendo eviterete tante volte errori di segno!
x^2 -6x+12 =0
Ora, calcoliamo il Delta quarti, essendo il coefficiente b pari.
\frac{\Delta}{4} = (\frac{b}{2})^2 - ac = 9-12= 1-3 =-2<0
Discriminante negativo e quindi non c’è nessuna soluzione all’equazione!
Esercizio 13. 12(y^2 -1) =-7y
Ora abbiamo la y anzichè la x, cosa cambia? Esattamente nulla! L’incognita si può chiamare in qualsiasi modo. Chiamare l’incognita come x è semplicemente una convenzione. Quindi facciamo il procedimento tale e quale! Sciogliamo la parentesi tonda:
12y^2 -12 =-7y
Portiamo il -7y a primo membro, cambiandolo di segno.
12y^2 -12 +7y =0
12y^2 +7y -12 =0
Ok, a questo punto, calcoliamo il Delta.
\Delta = b^2 - 4ac = 49 +576 = 625
Calcoliamo le due soluzioni distinte:
x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{-7 \pm 25 }{24}
E quindi abbiamo:
x_1 = \frac{-7 + 25 }{24} = \frac{18}{24} = \frac{9}{12} =\frac{3}{4}
x_2 = \frac{-7 - 25 }{24} = - \frac{32}{24}=- \frac{4}{3}
Esercizio 14. 0,25z^2 +z -0,5 =0
Qui vale lo stesso discorso di un paio di esercizi fa: l’incognita ha semplicemente un nome diverso ma in sostanza non cambia nulla. Di fatti andiamo subito a calcolare il discriminante. Anche con i numeri decimali se non sapete se il coefficiente b è pari o dispari, usate sempre la formula normale del delta:
\Delta = b^2 - 4ac = 1 +0,5 = 1,5
Discriminante positivo, e quindi ci aspettiamo due soluzioni:
x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{-1 \pm \sqrt{1,5} }{0,5}
E quindi:
x_1 = \frac{-1 + \sqrt{1,5} }{0,5}
x_1 = \frac{-1 - \sqrt{1,5} }{0,5}
Continuiamo con altri esercizi svolti equazioni di secondo grado!
Equazioni di secondo grado con parametri
Esercizio 15. Calcola le soluzioni dell’equazione di secondo grado seguente, senza discutere al variare del paramtero a:
x^2 - 2ax +a^2 =0
Allora, quando la traccia non ci chiede la discussione al variare del parametro, allora dobbiamo considerare il parametro come una costante, cioè come un qualsiasi numero. Quindi, come se non fosse cambiato nulla dagli altri esercizi, calcoliamo il discriminante.
Qui il coefficiente b è: -2a, e non sappiamo quindi se è pari o no. Questo perchè se a=1,5 il coefficiente ad esempio è dispari. Perciò usiamo la formula classica. Attenzione a non confondervi col la a nella formula che è tutto il coefficiente:
\Delta = b^2 - 4ac = 4a^2 - 4a^2 = 0
Il discriminante è nullo, perciò ci aspettiamo due soluzioni coincidenti. Il ragionamento è sempre lo stesso!
x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{2a }{2} = a
Esercizio 16. Calcola il parametro k affinché l’equazione seguente risulti avere discriminante nullo.
x^2 - kx +5k^2 =0
La traccia dell’esercizio è chiara: dobbiamo calcolare il discriminante, e fare in modo che questo risulti zero.
\Delta = b^2 - 4ac = k^2 - 20k^2 = -19k^2
Ora dobbiamo fare in modo che il Delta risulti zero, quindi vediamo per quale parametro k, il Delta risulta essere nullo. Calcoliamo:
\Delta = 0
-19k^2= 0
Dobbiamo vedere quali valori di k fanno sì che questo sia vero. Anche questa, se con due termini in meno, è una equazione di secondo grado. Essa risulta essere vera solo chiaramente per k=0. Perchè -19 moltiplicato per qualcosa fa zero, solo se k^2 fa zero. E quindi k=0.
Ed allora, per k=0 abbiamo che l’equazione iniziale risulta avere discriminante nullo.
Continuiamo con altre equazioni di secondo grado con esercizi svolti!
Esercizio 17. Calcola le soluzioni dell’equazione seguente, al variare del parametro m.
2\sqrt{2}mx - \sqrt{2}mx^2 =0
Le equazioni con il parametro devono essere trattate come le altre. Cerchiamo innanzitutto quindi di ordinare l’equazione.
- \sqrt{2}mx^2 + 2\sqrt{2}mx =0
Poi cambiamo tutto di segno, ed abbiamo l’equazione ben ordinata.
\sqrt{2}mx^2 - 2\sqrt{2}mx =0
Ora, abbiamo l’equazione nella forma:
ax^2 +bx + c=0
Notate però che il coefficiente c=0!
Poi il coefficiente a= \sqrt{2}m
Ed il coefficiente b=-2 \sqrt{2}m
Ed allora calcoliamo il discriminante innanzitutto, questa volta però dobbiamo commentare cosa succede al variare del parametro m, e vedremo come si fa.
\Delta = b^2 - 4ac = 8m^2
Adesso dobbiamo discutere cosa succede al variare di m. Abbiamo tre casi sempre:
- Abbiamo \Delta >0 e quindi 8m^2 >0 per qualsiasi m diversa da zero. Questo perchè abbiamo una m al quadrato, e quindi sicuramente positivo; però se esso è uguale a zero allora essa non saraà più >0. Quindi abbiamo discriminante positivo \forall m \ne 0
- Abbiamo \Delta =0 e quindi 8m^2 =0 se m=0! Quindi discriminante nullo se e solo se m=0.
- Abbiamo \Delta <0 e quindi 8m^2 <0 per nessuna m! Questo perchè esso è sicuramente positivo, essendo un singolo quadrato, moltiplicato per 8 che è positivo. Al massimo è zero, ma mai negativo.
Abbiamo discusso i tre casi. Calcoliamo le soluzioni adesso.
Per \forall m \ne 0 abbiamo discriminante positivo, e le due soluzioni sono:
x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{ 2\sqrt{2}m \pm \sqrt{8m^2} }{2\sqrt{2}m}
E lasciamo tutto così.
Poi abbiamo il caso in cui m=0 e quindi discriminante nullo, ed in questo caso la soluzione è:
x_{1,2} = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{ 2\sqrt{2}m }{2\sqrt{2}m} = 1
E poi abbiamo l’ultimo caso che però non si verifica mai, quindi non possiamo calcolare nessuna soluzione.
Continuiamo con altri esercizi svolti equazioni di secondo grado!
Equazioni di secondo grado per sostituzione
Esercizio 19. 4(\frac{x+3}{2-x})^2 -4(\frac{x+3}{2-x}) =-1
Qui possiamo notare una cosa a colpo d’occhio. Le quantità in parentesi sono uguali, e nelle situazioni come queste possiamo effettuare una sostituzione. Cioè facciamo una sostituzione di cambiamento di variabili e poniamo:
y=\frac{x+3}{2-x}
E possiamo riscrivere l’equazione in termini della y quindi come:
4y^2 -4y =-1
Adesso abbiamo una equazione che sappiamo risolvere. Portiamo il -1 dall’altra parte e poi calcoliamo il discriminante.
4y^2 -4y +1 =0
\frac{\Delta}{4} = (\frac{b}{2})^2 - ac = 16- 16= 0
Abbiamo quindi due soluzioni coincidenti:
y=\frac{-\frac{b}{2} \pm 0 }{a} = \frac{2}{4}= \frac{1}{2}
L’esercizio però non è finito, perchè vogliamo le soluzioni della x, e non della y! Quindi ricordiamo che:
y=\frac{x+3}{2-x}
Sappiamo quanto vale la y, quindi possiamo scrivere:
\frac{1}{2}=\frac{x+3}{2-x}
A questo punto diventa una equazione normale. Moltiplichiamo tutto per 2-x:
\frac{1}{2} (2-x) =x+3
1 - \frac{1}{2}x =x+3
Questa è una equazione lineare. Portiamo le x da una parte e i termini noti dall’altra:
- \frac{1}{2}x -x =3 -1
- \frac{3}{2}x =2
Moltiplichiamo tutto per 2, e poi dividiamo tutto per -3, in modo da isolare la x.
x =- \frac{4}{3}
E siamo arrivati alla soluzione della x!
Esercizio 20. (\frac{2a-1}{a})^2 - \frac{4a-2}{a} + \frac{3}{4}= 0
Qui non c’è nulla di uguale per il momento per fare una sostituzione. Però possiamo notare che possiamo mettere in evidenza il 2 come segue:
(\frac{2a-1}{a})^2 - \frac{2(a-1)}{a} + \frac{3}{4}= 0
E quindi:
(\frac{2a-1}{a})^2 - 2 \frac{a-1}{a} + \frac{3}{4}= 0
Ed ora, abbiamo fatto comparire due termini uguali e quindi come fatto prima, possiamo procedere con una sostituzione:
y= \frac{a-1}{a}
E quindi l’equazione di secondo grado diventa:
y^2 - 2y + \frac{3}{4}= 0
Questa la sappiamo fare sicuramente. Calcoliamo il discriminante:
\frac{\Delta}{4} = (\frac{b}{2})^2 - ac = 1- \frac{3}{4}= \frac{1}{4}
E le due soluzioni sono:
y_{1,2} = 1 \pm \frac{1}{2}
Ossia:
y_1 = 1 + \frac{1}{2} = \frac{3}{2}
y_2 = 1 - \frac{1}{2} = \frac{1}{2}
Ora risostituendo abbiamo, a differenza dell’esercizio precedente, due altre equazioni da risolvere. Questo perchè abbiamo:
\frac{3}{2}= \frac{a-1}{a}
\frac{1}{2}= \frac{a-1}{a}
Dobbiamo fare una cosa per volta, non spaventiamoci. Iniziamo a concentrarci sulla prima.
\frac{3}{2}= \frac{a-1}{a}
Moltiplichiamo tutto per a:
\frac{3}{2}a= a-1
\frac{3}{2}a- a= -1
\frac{3}{2}a- a= -1
\frac{1}{2}a= -1
Moltiplichiamo tutto per 2, ed abbiamo la prima soluzione dell’esercizio:
a= -2
Adesso concentriamoci sulla seconda equazione, ossia:
\frac{1}{2}= \frac{a-1}{a}
Moltiplichiamo per a.
\frac{1}{2}a= a-1
\frac{1}{2}a - a = -1
- \frac{1}{2}a = -1
Moltiplichiamo per -2, ed abbiamo anhce la seconda soluzione dell’esercizio, ed abbiamo completato l’esercizio! Lunghetto però facendo una cosa alla volta, si fa tutto!
a = 2
Continuate a studiare sul nostro sito con altre centinaia di esercizi sia di matematica che altro ancora!
Per approfondire: https://it.wikipedia.org/wiki/Equazione_di_secondo_grado
Cramer
di 2° grado
