Dominio di una funzione fratta: esercizi svolti
In questa pagina vediamo altri esercizi extra riguardo al dominio di una funzione fratta. Nella pagina di esercizi del dominio, abbiamo calcolato il dominio di tantissime diverse funzioni. Qui approfondiamo il dominio di una funzione fratta.
Ripetiamo che il dominio di una funzione fratta è il seguente. Cioè denominatore diverso da zero.
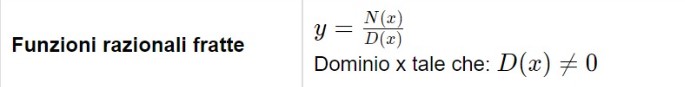
Esercizio extra 1. y = \frac{1}{ (2x^2 -4x)(x+3) }
Il discorso non cambia: questa è una pura funzione fratta, quindi dobbiamo porre denominatore diverso da zero.
D: \; (2x^2 -4x)(x+3) \ne 0
Questa, seppur con un disuguale, è una equazione, in cui vi compare un prodotto. Di conseguenza abbiamo che bisogna porre diverso da zero sia il primo pezzo che il secondo. Partiamo dal primo:
2x^2 -4x \ne 0 \implies 2x (x -2) \ne 0
A sua volta abbiamo un altro prodotto. Quindi deve risultare:
2x \ne 0 \implies x \ne 0
E poi anche ovviamente:
x-2 \ne 0 \implies x \ne 2
Teniamo da parte questi due risultati. Adesso passiamo al porre diverso da zero il secondo pezzo della frazione, che abbiamo messo da parte all’inizio.
x+3 \ne 0 \implies x \ne -3
Uniamo tutti i risultati ottenuti, perché nel dominio si considera tutto insieme contemporaneamente. Otteniamo:
D: \; x \ne 0 \land x \ne 2 \land x \ne -3
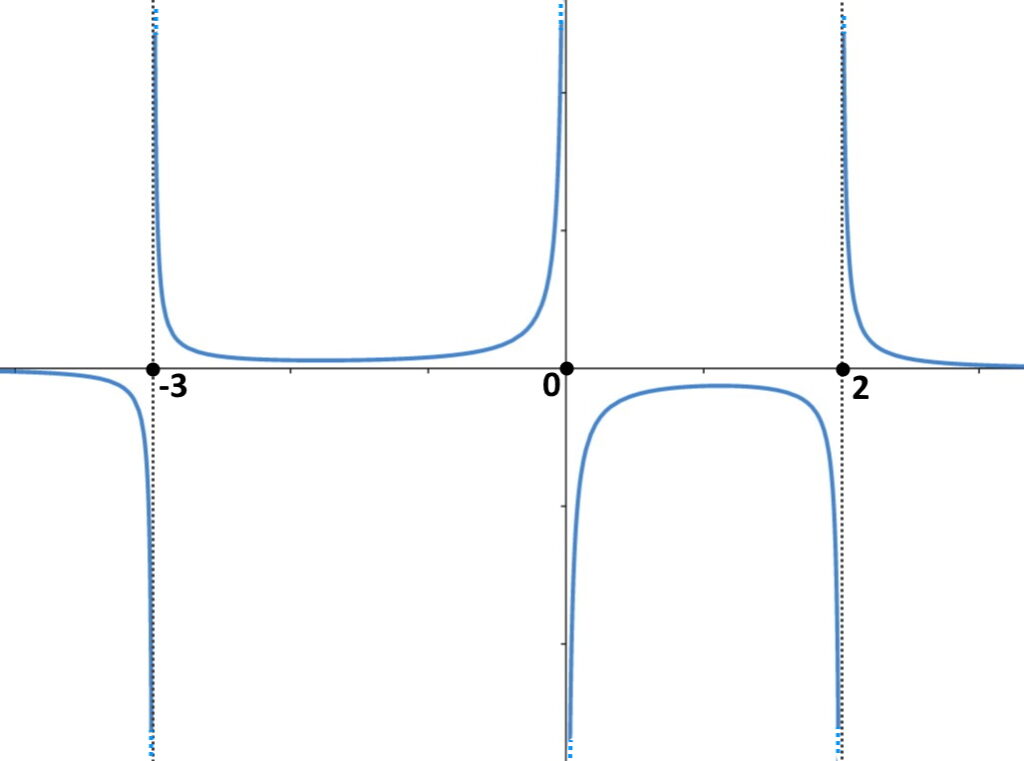
E questo è il dominio della funzione fratta dell’esercizio. Potete notare nel grafico questi punti particolari in cui la funzione non esiste, ossia non c’è nessuna y corrispondente a tali punti.
Esercizio extra 2. y = \frac{x^2 -3x +1}{ x^3 -2x +4 }
Chiaramente ormai sappiamo cosa dobbiamo fare, ed è:
D: \; x^3 -2x +4 \ne 0
Questa è una equazione (con \ne, ma non cambia nulla) di grado superiore al secondo. Non possiamo inoltre mettere in evidenza nulla, quindi dobbiamo scomporre utilizzando Ruffini. Con Ruffini dobbiamo cercare un valore da sostituire alla x, tale che risulti tutto zero. Il numero in questione è x=-2, di fatti in tal modo:
(-2)^3 -2 \cdotp (-2) +4 = -8 +4+4 = 0
Da qui si ha Ruffini.
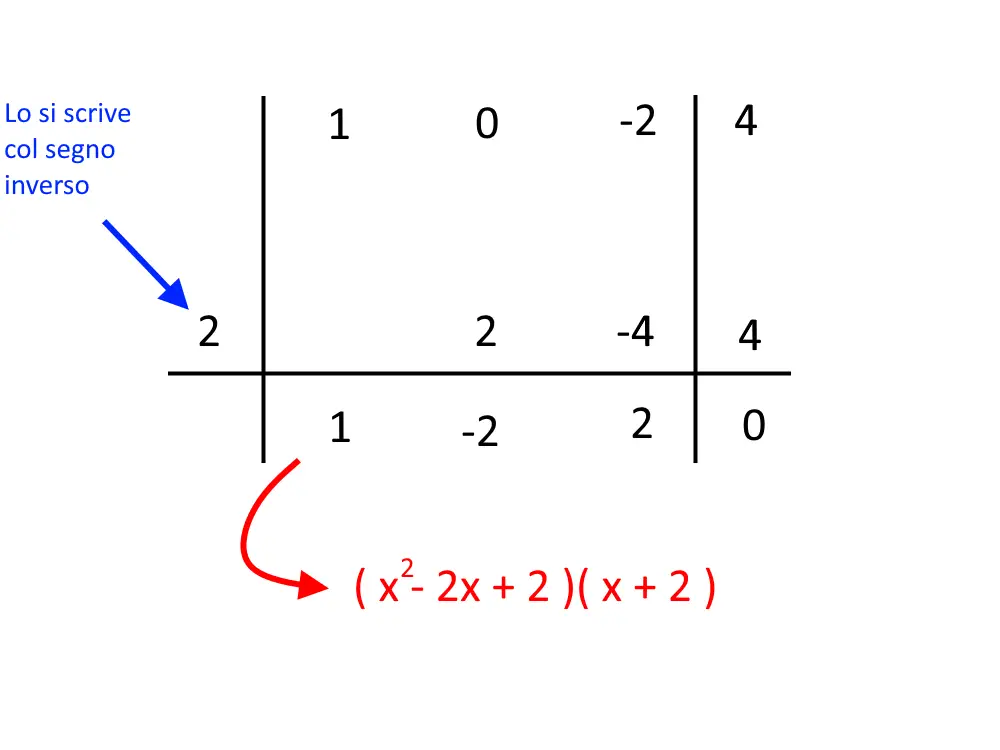
Ciò che viene fuori è quindi che l’espressione può essere riscritta come:
x^3 -2x +4 = (x^2 -2x +2)(x+2)
A questo punto il dominio è di più facile forma per essere calcolata!
D: \; (x^2 -2x +2)(x+2) \ne 0
Come nell’esercizio di prima, vi è un prodotto. Di conseguenza sia:
x^2 -2x +2 \ne 0
Equazione di secondo grado, quindi calcoliamo il delta-quarti (visto che il coefficiente b è pari):
\frac{\Delta}{4} = (\frac{b}{2})^2 -ac = 1 -2 = -1
Essendo il delta-quarti < 0 non vi è soluzione. Quindi non dobbiamo escludere nessun punto dal dominio per questo pezzo!
E poi il secondo pezzo:
x+2 \ne 0 \implies x \ne -2
Il dominio è solamente questo:
D: \; x \ne -2
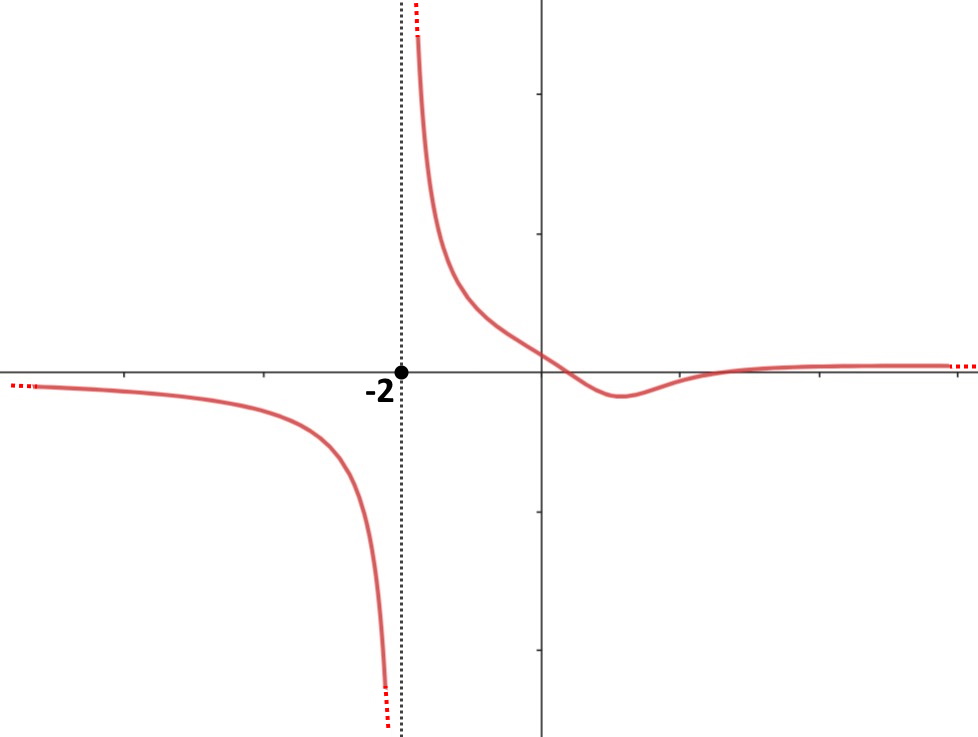
Comprensibile, vedendo il grafico di questa funzione.
Esercizio extra 3. y = \frac{x-3}{ x^4 -3x^2 +2 }
Qui non bisogna confondersi, perché potrebbe sembrare che si deve applicare Ruffini, ma non è così. Questa è riconducibile ad una equazione di secondo grado, grazie alla sostituzione:
t = x^2
Di conseguenza il dominio:
D: \; x^4 -3x^2 +2 \ne 0
Diventa più facile:
D: \; t^2 -3t +2 \ne 0
Questa la sappiamo risolvere, calcoliamone il delta:
\Delta = b^2 - 4ac = 9 -8 = 1
E le due soluzioni (dove alla fine bisogna mettere il \ne ovviamente) sono:
t_{1,2} = \frac{-b \pm \sqrt{ \Delta } }{2a} = \frac{3 \pm 1 }{2}
Nella nuova variabile t si ottiene quindi:
t_1 \ne \frac{3 + 1 }{2} = 2
t_2 \ne \frac{3 - 1 }{2} = 1
Adesso però è tempo di ritornare alla variabile x iniziale chiaramente!
t = x^2 \implies x^2 = 2 \implies x = \pm \sqrt{2}
E poi l’altra soluzione:
t = x^2 \implies x^2 = 1 \implies x = \pm 1
Nella scrittura del dominio finale, noi dobbiamo scartare queste soluzioni! Esso risulta quindi essere:
D: \; x \ne \pm 1 \land x \ne \pm \sqrt{2}
Esercizio extra 4. y = \frac{1}{ 1+ \frac{1}{ 1+ \frac{1}{x} } }
Sembra davvero essere complicato, in effetti vi sono tante cose da considerare. Non vi è un solo denominatore…ma ce ne sono ben tre! Di fatti essa è una frazione di frazione, quindi vi si devono considerare più diverse frazioni. La prima frazione, quella principale presenta un numeratore principale che è 1, poi il denominatore principale è:
D: \; 1+ \frac{1}{ 1+ \frac{1}{x} } \ne 0
Scalando, notiamo nella traccia dell’esercizio, la presenza di una seconda frazione \frac{1}{ 1+ \frac{1}{x} }. Per questa il suo denominatore è:
D: \; 1+ \frac{1}{x} \ne 0
Infine, notiamo la presenza di una terza frazione che è \frac{1}{x}. Il suo denominatore, e di conseguenza ques’altro aggiuntivo dominio sarà:
D: \; x \ne 0
Abbiamo tre domini da considerare, e da unire alla fine! Il terzo è ovvio, ossia x \ne 0 . Passiamo al secondo:
1+ \frac{1}{x} \ne 0
Dobbiamo risolverla. Questa è una equazione fratta, facciamo per cui il minimo comune multiplo:
\frac{x+1}{x} \ne 0 \implies x+1 \ne 0 \implies x \ne -1
Ed ecco il secondo punto da scartare. Passiamo ora al primo dominio che abbiamo scritto:
1+ \frac{1}{ 1+ \frac{1}{x} } \ne 0
Risolviamola! Questa è più complicata, iniziamo a fare il minimo comune multiplo sotto:
1+ \frac{1}{ \frac{x+1}{x} } \ne 0
Invertiamo quella frazione di frazione:
1+ \frac{x}{x+1} \ne 0
E poi:
\frac{x+1+x}{x+1} \ne 0
\frac{2x+1}{x+1} \ne 0 \implies 2x+1 \ne 0 \implies x \ne - \frac{1}{2}
A questo punto abbiamo trovato tre numeri in totali da scartare. Il dominio della funzione è:
D: \; x \ne 0 \land x \ne -1 \land x \ne - \frac{1}{2}
Questa è la procedura corretta da seguire; non potete fare passaggi o calcoli direttamente all’inizio prima di scrivere il dominio. Bisogna prima scrivere il dominio della funzione che si vede nella traccia dell’esercizio. Se fate calcoli all’inizio direttamente sulla funzione, state modificando la funzione stessa!
Abbiamo finito con gli esercizi extra sul calcolo del dominio di una funzione fratta.
Tornate nella pagina degli esercizi sul dominio delle funzioni! Continuate a studiare sul nostro sito!
Trovate poi altri centinaia di argomenti di Matematica, geometria analitica o geometria!
funzione