Disequazioni con valore assoluto ESERCIZI
Disequazioni con valore assoluto ESERCIZI: 15 esercizi svolti! In questa pagina risolveremo tutti i tipi di disequazioni con valore assoluto e ne vedremo tutti i casi spiegati passo dopo passo. Assicuratevi almeno di sapere le basi delle equazioni con valore assoluto prima! Partiamo subito!
Indice
- Disequazioni della forma: |f(x)| \ge k
- Disequazioni della forma: |f(x)| \le k
- Disequazioni della forma: |f(x)| \lessgtr g(x)
- Disequazioni con più valori assoluti
Iniziamo subito a risolvere delle disequazioni con valore assoluto esercizi svolti!
Disequazioni con valore assoluto
|f(x)| \ge k
Durante questa prima parte di esercizi sarà questa la formula che seguiremo.

Esercizio 1. | 6x-3 | > 1
L’equazione è proprio della stessa forma della formula sopra citata: ossia abbiamo a sinistra solo un valore assoluto e a destra un numero. Quindi applichiamo la formula direttamente senza fare ulteriori passaggi:
\implies 6x-3 < -1 \lor 6x-3 > 1
(Qui non c’è l’uguale anche perché bisogna sempre mantenere gli stessi segni della disequazione dell’esercizio).
La logica però è sempre la stessa per le disequazioni: anche qui come vedete c’è un maggiore e di fatti prendiamo i valori esterni.
Nelle disequazioni questo accade quasi sempre nelle formule.
Comunque torniamo all’esercizio. Risolviamo uno per volta separatamente ogni disequazione. Partiamo dalla prima:
6x-3 < -1
Essa è una semplice disequazione, quindi isoliamo la x:
6x < -1+3
Poi dividiamo per 6.
x < \frac{2}{6}
Ossia semplificando col 2:
x < \frac{1}{3}
Ed il primo termine è risolto, adesso passiamo alla seconda disequazione!
6x-3 > 1
6x > 4
Dividiamo per 6 ed otteniamo il secondo intervallo di soluzioni:
x > \frac{2}{3}
A questo punto dobbiamo mettere insieme queste due soluzioni mantenendo la forma originaria, ossia mettendo fra le due sempre un \lor . Quindi:
x < \frac{1}{3} \lor x > \frac{2}{3}
L’esercizio è concluso!
Esercizio 2. 3| x-4 | - 12 \ge 0
Qui l’esercizio non è immediato come prima, però non ci sono molti passaggi da memorizzare in più: semplicemente per raggiungere la stessa forma della formula dobbiamo isolare a sinistra il valore assoluto. Cioè noi vogliamo solo il valore assoluto a primo membro, per poter applicare la formula.
Quindi iniziamo a portare il -12 a secondo membro:
3| x-4 | \ge 12
La forma non è ancora quella giusta, dividiamo per 3.
| x-4 | \ge 4
Adesso sì che possiamo applicare la formula! Quindi:
x-4 \le -4 \lor x-4 \ge 4
Come prima ne risolviamo uno alla volta separatamente. Iniziamo da:
x-4 \le -4
x \le -4+4 \implies x \le 0
Adesso passiamo all’altra:
x-4 \ge 4
\implies x \ge 8
Adesso è il momento di rimettere insieme le due soluzioni:
x \le 0 \lor x \ge 8
Quindi come potete ben vedere queste sono molto diverse dalle equazioni con valori assoluti.
Continuiamo con altre disequazioni con valore assoluto esercizi svolti!
Esercizio 3. | 5-x | +1 \ge 0
Questo è un ESERCIZIO IMPORTANTE!
Iniziamo ad isolare il valore assoluto, come visto prima. Quindi portiamo 1 a secondo membro:
| 5-x | \ge -1
Nei due esercizi precedenti abbiamo visto il caso in cui il numero a secondo membro era positivo o uguale a zero. Qui però è diverso, abbiamo un numero negativo. Come si procede?
A sinistra abbiamo un valore assoluto che per definizione è positivo o al massimo uguale a zero, quindi esso sarà SICURAMENTE maggiore di -1, sempre!
Quindi per qualsiasi x tale disequazione sarà soddisfatta. La soluzione è:
\forall x \in \Reals
Esercizio 4. | x^2 + x | > 6
La disequazione è già nella giusta forma, quindi utilizziamo la solita formula.
x^2 + x < - 6 \lor x^2 +x > 6
Ciò che dobbiamo fare è risolvere queste due disequazioni uno per volta. Partiamo dalla prima:
x^2 + x < - 6
Essa è una disequazione di secondo grado (se non vi ricordate cliccateci un attimo almeno per le formule). Per la risoluzione di una disequazione di secondo grado dobbiamo riordinarla prima:
x^2 + x +6 < 0
Calcoliamo il discriminante ( o delta, sono sinonimi):
\Delta = b^2 - 4ac = 1 - 24 = -23
Il delta<0, e visto che la disequazione ha un minore (<) significa che la soluzione di questa prima disequazione è:
\nexists x
Cioè per nessuna x.
Adesso passiamo alla seconda disequazione:
x^2 +x > 6
Come prima, anche questa è di secondo grado, quindi riordiniamola prima:
x^2 +x -6 >0
Calcoliamo quest’altro delta:
\Delta = b^2 - 4ac = 1 +24 = 25
Delta>0 e quindi esistono soluzioni. Calcoliamo le due singole soluzioni con la formula seguente, e poi prendiamone i valori esterni essendoci una disequazione con maggiore come segno (>).
x_{1,2} = \frac{-b \pm \sqrt{\Delta} }{2a} = \frac{-1 \pm 5 }{2}
E quindi:
x_1 = \frac{-1 + 5 }{2} = 2
x_2 = \frac{-1 - 5 }{2} = -3
E come detto prima, dobbiamo prendere i valori esterni. Se non vi ricordate queste cose cliccateci un attimo e vedete qualche esempio di come si risolve una disequazione di secondo grado.
La soluzione è:
x < -3 \lor x > 2
L’altra soluzione non la mettiamo perché sarebbe:
\nexists x \lor x < -3 \lor x > 2
E visto che il simbolo \lor significa unione, alla fine si prendono solo le soluzioni valide, cioè quelle scritte prima.
Continuiamo con altre disequazioni con valore assoluto esercizi svolti!
Disequazioni con valore assoluto
|f(x)| \le k
Adesso la formula è diversa. Seguiremo quest’altra.

Esercizio 5. | 3x + 1 | \le 5
Ora le disequazioni con valore assoluto hanno una forma diversa (il segno minore) e seguono una formula diversa sopra scritta.
La forma è quella giusta, ossia valore assoluto a sinistra da solo e a destra un numero.
Applichiamo la formula:
-5 \le 3x +1 \le 5
(Qui potete notare che c’è un minore ed infatti eccovi i valori interni). Se prima potevamo risolvere quelle due disequazioni separatamente, qui non possiamo farlo: dobbiamo per forza mettere a sistema queste due disequazioni, e quindi prendere le soluzioni in comune!
Risolviamo quindi il sistema:
\begin{cases} 3x+1 \le 5 \\ 3x+1 \ge -5 \end{cases}
\begin{cases} 3x \le 4 \\ 3x \ge -6\end{cases}
Dividiamo per 3, ed abbiamo così due soluzioni:
\begin{cases} x \le \frac{4}{3} \\ x \ge -2 \end{cases}
Mettere a sistema significa cercare le soluzioni in comune, ossia prendiamo il seguente schema e cerchiamo gli stessi intervalli.
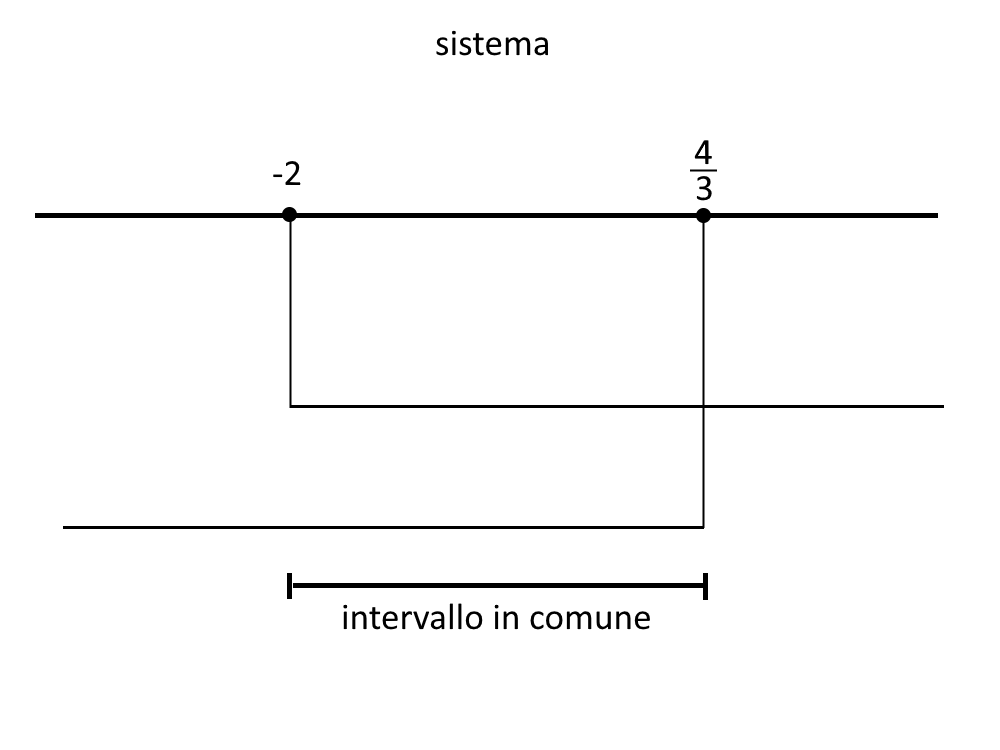
Ossia:
-2 \le x \le \frac{4}{3}
Esercizio 6. 6 - | x + 2 | > 0
Come primo punto iniziamo ad isolare a primo membro il valore assoluto, questo sempre.
- | x + 2 | > -6
Ciò non basta per applicare la formula perché vogliamo solo il valore assoluto, senza nient’altro. Quindi cambiamo tutto di segno ( e ricordatevi che quando si cambia tutto di segno una disequazione si cambia anche il segno stesso della disequazione, cioè ora diventa <).
| x + 2 | < 6
Adesso è della forma giusta. Risolviamo quindi il sistema:
\begin{cases} x+2 < 6 \\ x+2 > -6 \end{cases}
\begin{cases} x < 4 \\ x > -8 \end{cases}
Mettiamo ogni soluzione nello schema solito.
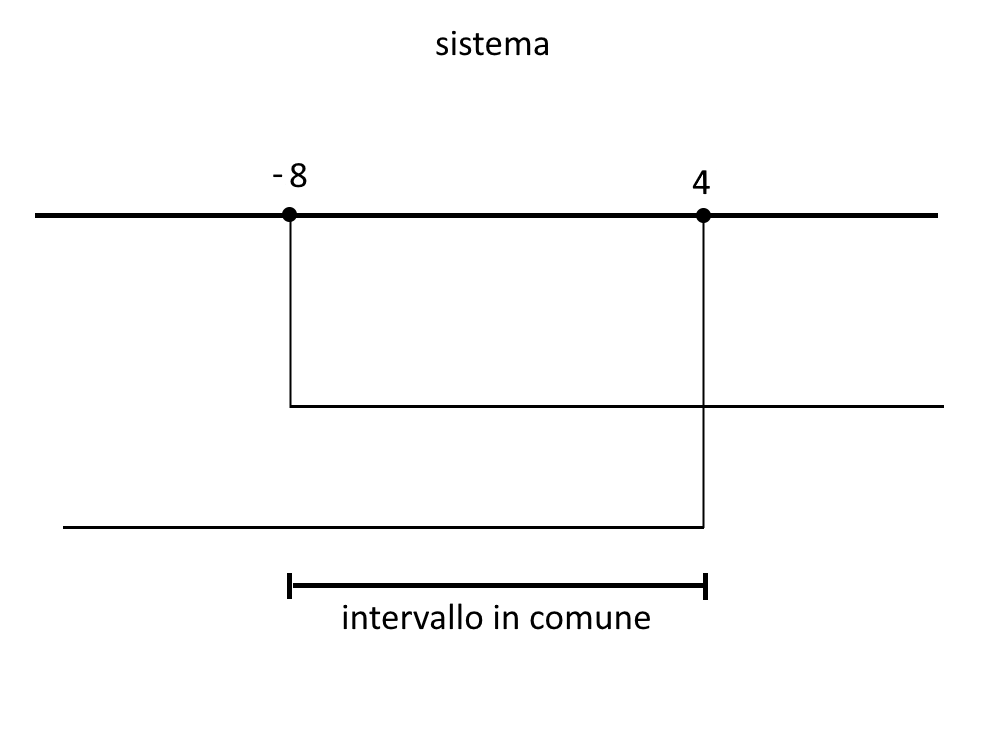
Ed essendo un sistema si prendono le soluzioni comuni. Quindi la soluzione finale è:
-8 < x < 4
Continuiamo con altre disequazioni con valore assoluto esercizi svolti!
Esercizio 7. 5 + | 2x - 3 | \le 0
Isoliamo il valore assoluto:
| 2x - 3 | \le -5
Ecco che abbiamo un valore assoluto a sinistra, però abbiamo poi un numero negativo a secondo membro.
Come si procede? Facciamo un discorso simile al precedente. Abbiamo a sinistra un valore assoluto per definizione positivo o uguale a zero. Esso quindi non può MAI essere più piccolo di un numero negativo, cioè più piccolo di -5. Ad esempio non può essere uguale a -6 né tanto meno a -7. Questo perché ripetiamo che un valore assoluto è per definizione \ge 0 !
Quindi la soluzione dell’esercizio è impossibile.
Esercizio 8. | 3x - 1-x^2 | \le 1
Come potete vedere non c’è nulla da fare, applichiamo direttamente la formula. Risolviamo direttamente il sistema seguente.
\begin{cases} 3x - 1-x^2 \le 1 \\ 3x - 1-x^2 \ge -1 \end{cases}
Entrambe sono disequazioni di secondo grado, quindi portiamo tutto a primo membro:
\begin{cases} 3x - 2-x^2 \le 0 \\ 3x -x^2 \ge 0 \end{cases}
Nella prima disequazione riordiniamo i termini, per poi così poter calcolare il discriminante. E poi nel secondo invece mettiamo in evidenza una x:
\begin{cases} -x^2 +3x -2 \le 0 \\ x(3 -x) \ge 0 \end{cases}
Nella disequazione di secondo grado è comodo ed importante che il termine con la x quadratica sia positivo, quindi cambiamo prima tutto di segno.
\begin{cases} x^2 -3x +2 \ge 0 \\ x(3 -x) \ge 0 \end{cases}
Adesso visto che non sono immediate, le risolviamo un attimo da parte singolarmente. Partiamo dalla prima, nella quale calcoliamo il delta:
\Delta = b^2 - 4ac = 9 -8 = 1
Delta>0 e quindi esistono soluzioni. Calcoliamo le singole soluzioni con la formula:
x_{1,2} = \frac{-b \pm \sqrt{\Delta} }{2a} = \frac{3 \pm 1 }{2}
Ed allora:
x_1 = \frac{3+1 }{2} = 2
x_2 = \frac{3 - 1 }{2} =1
Poi visto che è una disequazione con il segno di maggiore prendiamo i valori esterni di questi due numeri.
x \le 1 \lor x \ge 2
Sostituiamo nel sistema il dato ottenuto:
\begin{cases} x \le 1 \lor x \ge 2 \\ x(3 -x) \ge 0 \end{cases}
Ora ci rimane il secondo termine del sistema. Questo è un prodotto di due termini, e si risolve con un falso sistema scritto da parte.
\big\| x \ge 0 \\ \big\| 3-x \ge 0
\big\| x \ge 0 \\ \big\| x \le 3
Prendiamo l’intervallo positivo col segno + nel quadro dei segni, perché la disequazione è con un maggiore.
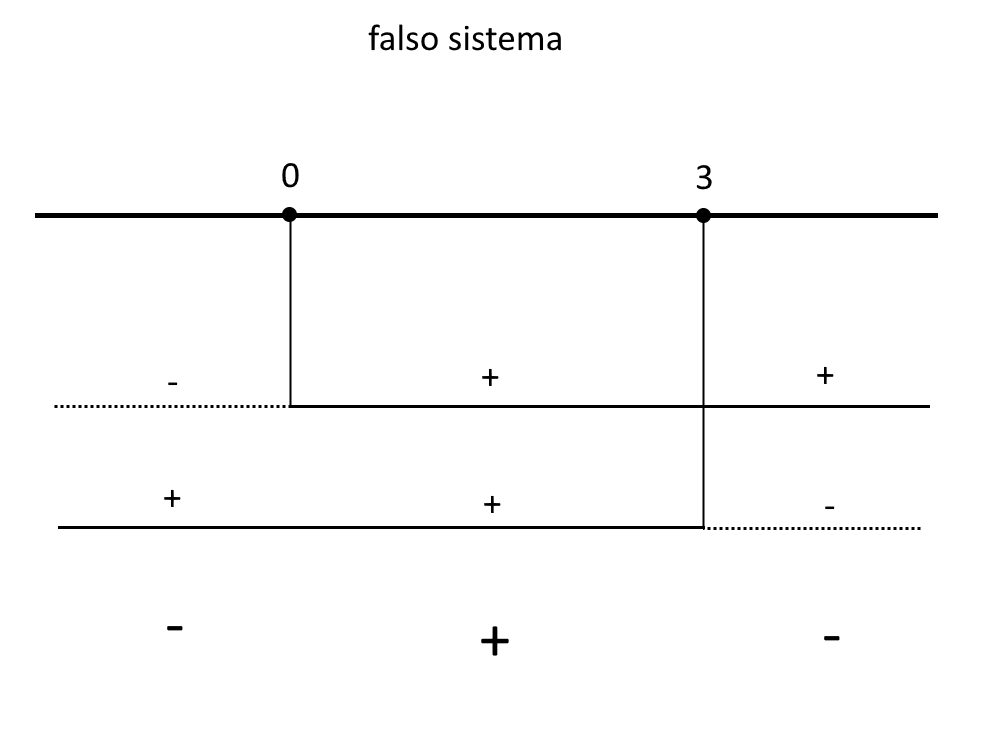
Quindi:
0 \le x \le 3
Adesso sostituiamo anche questo risultato nel sistema iniziale, ed andiamo finalmente a concludere l’esercizio.
\begin{cases} x \le 1 \lor x \ge 2 \\ 0 \le x \le 3 \end{cases}
Prendiamo gli intervalli comuni, essendo un sistema, ed abbiamo come soluzione dell’esercizio:
0 \le x \le 1 \lor 2 \le x \le 3
Continuiamo con altre disequazioni con valore assoluto esercizi svolti!
Disequazioni della forma
|f(x)| \lessgtr g(x)
Vediamo che formula utilizzeremo in questo capitoletto. E’ importantissimo alla fine di capire come si svolgono questi esercizi, soprattutto l’esercizio 12.
La formula è uguale, qui vedete anche degli esempi in cui come vedete cambia solo il segno del secondo termine dei sistemi. Quindi basta imparare a memoria uno solo!

Esercizio 9. | x - 3 | < 3x - 1
In questo capitoletto di esercizi abbiamo una equazione con: a primo membro un valore assoluto, e a secondo membro un qualcosa contenente la x, mentre prima avevamo solamente un numero se vi ricordate.
Una volta raggiunta questa forma, possiamo applicare la formula sopra scritta come vedete. Qui la formula consiste nel risolvere ben due sistemi svolti separatamente! Scriviamoli:
\begin{cases} x -3 \ge 0 \\ x-3<3x-1 \end{cases} \lor \begin{cases} x -3< 0 \\ -(x-3)<3x-1 \end{cases}
In tutte queste quattro disequazioni cerchiamo di isolare la x a primo membro e quindi di risolverle come sappiamo fare!
\begin{cases} x \ge 3 \\ -2x<2 \end{cases} \lor \begin{cases} x < 3 \\ -x-3x<-1-3 \end{cases}
Al secondo termine del primo sistema e del secondo sistema cambiamo di segno tutto e poi dividiamo per 2 (ricordate di cambiare anche il segno della disequazione).
\begin{cases} x \ge 3 \\ x>-1 \end{cases} \lor \begin{cases} x < 3 \\ x>1 \end{cases}
A questo punto pensiamo ad uno alla volta in maniera distinta. Pensiamo al primo sistema. La soluzione comune è:
x \ge 3
Passiamo al secondo: x>1
Adesso bisogna UNIRE queste due singole soluzioni. Visto che il simbolo \lor significa unione, dobbiamo unire la soluzioni con un nuovo schema. Mettiamo tutte le soluzioni su una unica riga come segue.
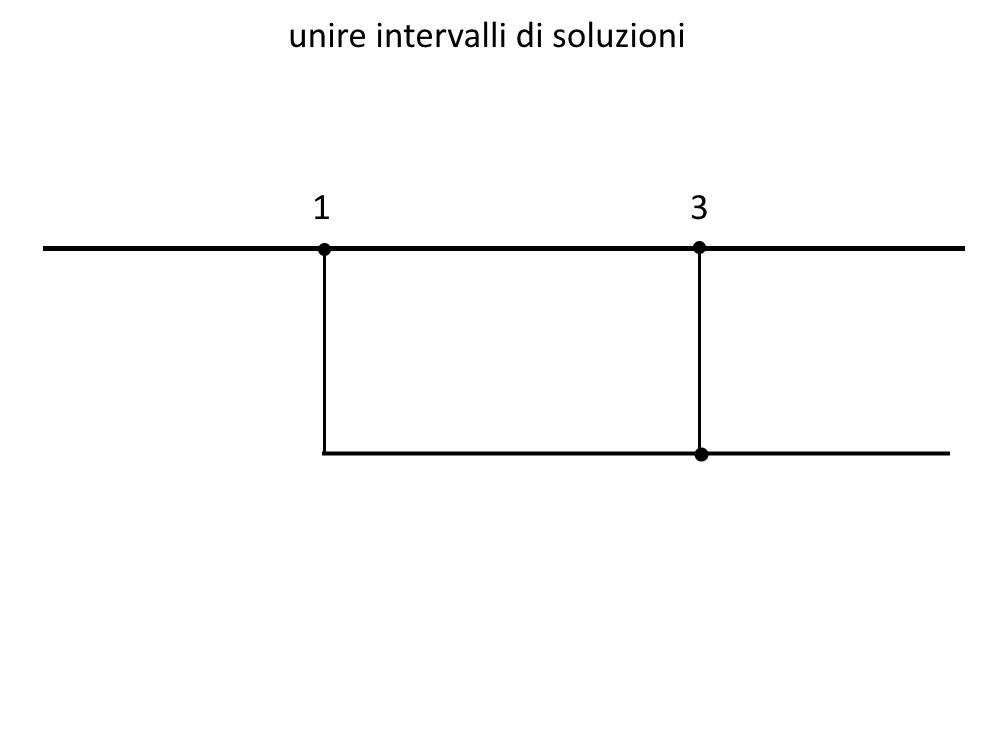
E poi prendiamo il grande intervallo di soluzioni che ne è uscito, quindi:
x>1
Esercizio 10. 2x - | x - 3 | \le 1
Per ottenere la forma della formula esatta: quindi valore assoluto a sinistra e tutto il resto a destra, andiamo a portare il 2x a secondo membro:
- | x - 3 | \le 1-2x
Non basta, perché quel – non lo vogliamo davanti al valore assoluto, quindi cambiamo tutto di segno.
| x - 3 | \ge -1+2x
Ora possiamo applicare la formula e risolvere i due sistemi.
\begin{cases} x -3 \ge 0 \\ x - 3 \ge -1+2x \end{cases} \lor \begin{cases} x -3< 0 \\ -(x - 3) \ge -1+2x \end{cases}
\begin{cases} x \ge 3 \\ x - 3 \ge -1+2x \end{cases} \lor \begin{cases} x <3 \\ -x + 3 \ge -1+2x \end{cases}
Risolviamo le ultime due disequazioni dei due sistemi, ed otteniamo:
\begin{cases} x \ge 3 \\ x \le -2 \end{cases} \lor \begin{cases} x <3 \\ x \le \frac{4}{3} \end{cases}
Riguardo il primo sistema otteniamo una soluzione comune di:
\nexists x
Mentre nel secondo sistema otteniamo un intervallo comune di soluzioni:
x \le \frac{4}{3}
Uniamo le due soluzioni adesso.
\nexists x \lor x \le \frac{4}{3}
Quando c’è di mezzo \nexists x in una unione esso non dà contributo, quindi lo si leva, e la soluzione finale è:
x \le \frac{4}{3}
PICCOLA NOTA!
Discorso diverso se avevamo invece un qualcosa per esempio:
\forall x \lor x \le \frac{4}{3}
Quando c’è invece un \forall x in una unione è questo che domina e quindi la soluzione finale è:
\forall x
Quindi il contrario del caso precedente!
Esercizio 11. | x^2 - 2x | > 2x+5
Abbiamo come vedete nella formula la disequazione nella forma giusta: valore assoluto a sinistra da solo, e il resto con una x a destra. Risolviamo subito i due sistemi:
\begin{cases} x^2 -2x \ge 0 \\ x^2 - 2x > 2x+5 \end{cases} \lor \begin{cases} x^2 -2x < 0 \\ -(x^2 - 2x ) > 2x+5 \end{cases}
Abbiamo delle disequazioni di secondo grado. Dobbiamo, per non confonderci con troppi calcoli, calcolarli uno per volta da parte. Per il primo termine del primo sistema basta semplicemente mettere in evidenza:
x^2 -2x \ge 0 \implies x (x-2) \ge 0
Questo l’abbiamo visto tante volte e si risolve con un falso sistema.
\big\| x \ge 0 \\ x-2 \ge 0 \big\|
\big\| x \ge 0 \\ x \ge 2 \big\|
Prendiamo gli intervalli positivi nel quadro dei segni e quindi:
x \le 0 \lor x \ge 2
Per quanto riguarda l’altro primo termine del secondo sistema, l’unica differenza è il segno.
x^2 -2x < 0 \implies x (x-2) < 0
Potete risolverlo comunque, però quando c’è come differenza solo il segno della disequazione allora il risultato è lo stesso ma con segni diversi. Quindi qui sarà con valori interni:
0 \le x \le 2
Ripeto che se non siete sicuri o convinti fate lo stesso i calcoli! No problem!
Adesso dobbiamo calcolare la seconda disequazione di secondo grado del primo sistema:
x^2 - 2x > 2x+5
Riordiniamola:
x^2 - 4x -5 > 0
Calcoliamo il discriminante, o delta-quarti visto che qui abbiamo il coefficiente b (cioè il secondo) pari. Quindi usiamo quest’altra formula:
\frac{\Delta}{4} = (\frac{b}{2})^2 - ac = 4+5 = 9
Discriminante>0 in una disequazione con >, e quindi esistono soluzioni. Calcoliamo le singole soluzioni e poi prendiamone i valori esterni (perché c’è un maggiore nella disequazione).
x_{1,2} = \frac{-\frac{b}{2} \pm \sqrt{ \frac{\Delta}{4} } }{a}= \frac{ 2 \pm 3 }{1}
Ossia:
x_1 = \frac{ 2 + 3 }{1} = 5
x_2 = \frac{ 2 - 3 }{1} =-1
E poi come detto prima si prendono i valori esterni:
x < -1 \lor x > 5
Adesso risolviamo l’ultima disequazione, la seconda del secondo sistema!
-(x^2 - 2x ) > 2x+5
-x^2 + 2x > 2x+5
Semplifichiamo il 2x:
-x^2 > 5
Cambiamo tutto di segno:
x^2 < -5
Abbiamo un quadrato che per definizione è positivo o uguale a zero, che ovviamente non può MAI essere minore di -5, cioè più piccolo di un numero negativo, perché non è mai negativo un quadrato.
\implies \nexists x
Adesso abbiamo tutti e 4 i risultati, e possiamo finalmente sostituire tutto nei due sistemi iniziali:
\begin{cases} x \le 0 \lor x \ge 2 \\ x < -1 \lor x > 5 \end{cases} \lor \begin{cases} 0 \le x \le 2 \\ \nexists x \end{cases}
Nel secondo sistema non c’è nessuna soluzione chiaramente; nel primo sistema la soluzione comune è proprio:
x < -1 \lor x > 5
E qui non serve unire i due sistemi perché nel secondo non c’è soluzione, e quindi ci ridarebbe sempre questa soluzione scritta appena!
Esercizio 12. \frac{ x-6 }{ |x - 1| } > x+2
Prima di iniziare con la discussione, qui abbiamo una frazione, e quindi bisogna scrivere anche le condizioni di esistenza in questo caso. Per le frazioni è denominatore diverso da zero.
CE: |x-1| \ne 0 \implies x-1 \ne 0 \implies x \ne 1
Adesso passiamo alla discussione dell’esercizio. Quando, come in questo caso, è più difficile isolare un valore assoluto, allora andiamo a risolvere direttamente i due sistemi.
In pratica scriviamo le disequazioni così come sono stando attenti a cambiare di segno solo ai valori assoluti, nel secondo caso.
Vedete come scriviamo:
\begin{cases} x-1 \ge 0 \\ \frac{ x-6 }{ x - 1 } > x+2 \end{cases} \lor \begin{cases} x-1< 0 \\ \frac{ x-6 }{ -(x - 1) } > x+2 \end{cases}
\begin{cases} x \ge 1 \\ \frac{ x-6 }{ x - 1 } > x+2 \end{cases} \lor \begin{cases} x< 1 \\ \frac{ x-6 }{ 1-x } > x+2 \end{cases}
Iniziamo a risolvere il secondo termine del primo sistema da parte, che è una disequazione fratta.
\frac{ x-6 }{ x - 1 } > x+2
I passaggi da seguire per le disequazioni fratte sono: portare tutto a primo membro, fare il mcm, e poi risolvere il falso sistema.
Quindi iniziamo a:
\frac{ x-6 }{ x - 1 } -x-2 > 0
Facciamo il minimo comune multiplo:
\frac{ x-6-x(x-1)-2(x-1) }{ x - 1 } > 0
\frac{ x-6-x^2 +x -2x +2 }{ x - 1 } > 0
Sommiamo i rispettivi termini:
\frac{ -x^2 -4 }{ x - 1 } > 0
E risolviamo questo con un falso sistema.
\big\| -x^2 -4 > 0 \\ \big\| x -1 > 0
\big\| -x^2 > 4 \\ \big\| x > 1
Cambiamo di segno il primo termine.
\big\| x^2 < 4 \\ \big\| x > 1
Il primo si prendono le due radici di segno opposto, e poi i valori interni, essendoci un minore.
\big\| -2<x < 2 \\ \big\| x > 1
Prendiamo nel quadro dei segni gli intervalli positivi.
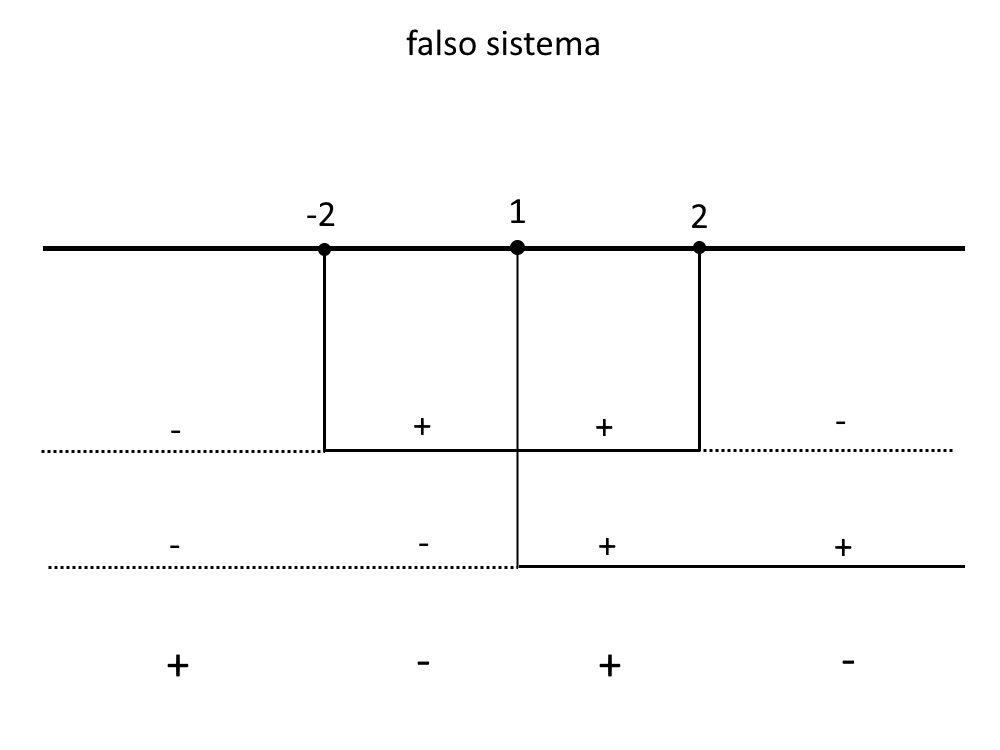
Ossia:
x<-2 \lor 1<x<2
Adesso passiamo a risolvere l’altra disequazione fratta, del secondo sistema.
\frac{ x-6 }{ 1-x } > x+2
Come prima seguiamo gli stessi passaggi.
\frac{ x-6 }{ 1-x } -x-2> 0
Facciamo il mcm:
\frac{ x-6 -x(1-x)-2(1-x)}{ 1-x } > 0
\frac{ x-6 -x+x^2-2+2x }{ 1-x } > 0
Sommiamo i termini corrispettivi al numeratore.
\frac{ x^2+2x -8}{ 1-x } > 0
E scriviamo il suo falso sistema.
\big\| x^2+2x -8 > 0 \\ \big\| 1-x > 0
\big\| x^2+2x -8 > 0 \\ \big\| x < 1
Calcoliamo il primo termine da parte, che è una disequazione di secondo grado. Scriviamo il discriminante:
\frac{\Delta}{4} = (\frac{b}{2})^2 - ac = 1+8 = 9
Delta-quarti>0 in una disequazione con segno (>) maggiore, allora esistono soluzioni. Troviamole:
x_{1,2} = \frac{-\frac{b}{2} \pm \sqrt{ \frac{\Delta}{4} } }{a}= \frac{ -1 \pm 3 }{1}
Ossia:
x_1 = \frac{ -1 + 3 }{1} = 2
x_2 = \frac{ -1 - 3 }{1} = -4
E poi ne prendiamo i valori esterni, essendo la disequazione con un maggiore.
x<-4 \lor x>2
Adesso abbiamo calcolato tutto: sostituiamo nei due sistemi!
\begin{cases} x \ge 1 \\ x<-2 \lor 1<x<2 \end{cases} \lor \begin{cases} x< 1 \\ x<-4 \lor x>2 \end{cases}
Nel primo sistema non c’è soluzione comune. Nel secondo sistema la soluzione in comune è:
x<-4
che è anche la soluzione dell’esercizio!
Essa inoltre rispetta anche le CE.
Quando gli esercizi sono così lunghi bisogna fare un passaggio alla volta SENZA FRETTA!
Continuiamo con altre disequazioni con valore assoluto esercizi svolti!
Disequazioni con più valori assoluti
Esercizio 15. | 9x - 3 | < | x+5 |
Quando ci sono più valori assoluti, cambia il procedimento dell’esercizio. Elencheremo tutti i passaggi. Il PRIMO PUNTO è porre i valori assoluti maggiori o uguale di zero:
9x-3 \ge 0 \implies x \ge \frac{1}{3}
x+5 \ge 0 \implies x \ge -5
Il SECONDO PUNTO è mettere in uno schema come quello seguente questi risultati.
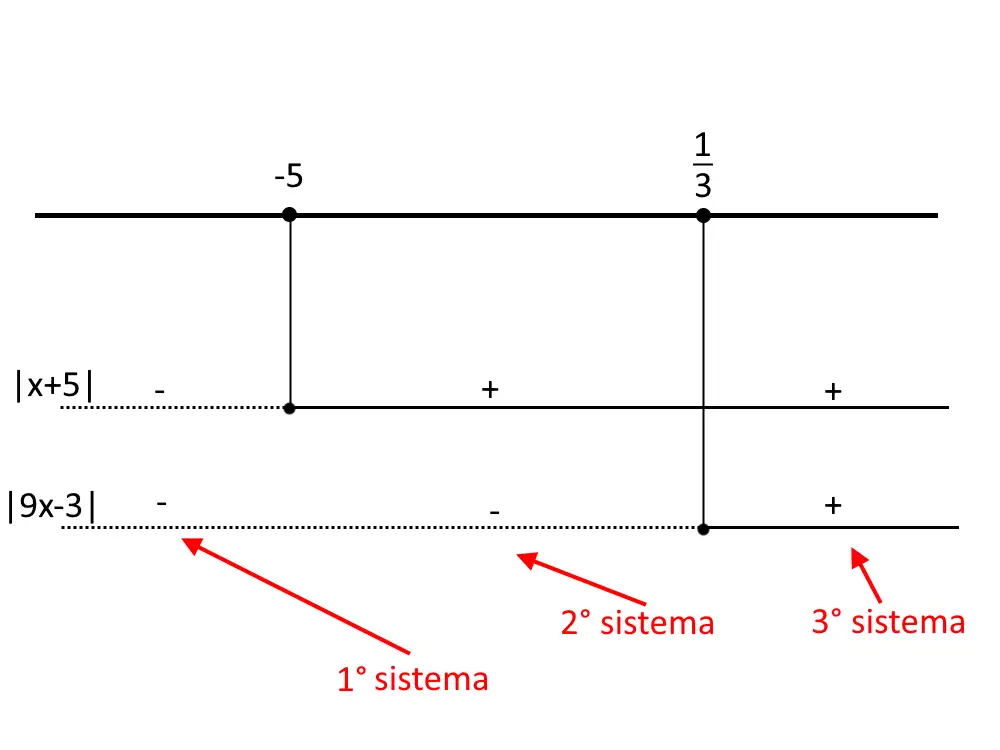
Come vedete è uno schema particolare e nuovo, non è il quadro dei segni. Tutti gli intervalli che abbiamo elencato nello schema è il numero totale di sistemi che bisognerà risolvere. Ogni sistema conterrà i valori assoluti con davanti un segno + o – a seconda di quale intervallo si trovano. Ad esempio nel primo intervallo sulla linea del |x+5| c’è un – e quindi dovremo scrivere -(x+5) nel sistema e così via. Stesso per l’altro valore assoluto.
Scriviamo i tre sistemi che dobbiamo risolvere:
\begin{cases} x \le -5 \\ -(9x - 3) < -(x+5) \end{cases} \lor \begin{cases} -5 \le x < \frac{1}{3} \\ -(9x - 3) < x+5 \end{cases} \lor \begin{cases} x \ge \frac{1}{3} \\ 9x - 3 < x+5 \end{cases}
Come vedete nel primo rigo di ogni sistema mettiamo l’intervallo. Al secondo rigo mettiamo la disequazione con i segni davanti ai rispettivi valori assoluti.
Sono passaggi molto delicati, bisogna stare attenti ai segni ed andare con calma.
\begin{cases} x \le -5 \\ -9x + 3 < -x-5 \end{cases} \lor \begin{cases} -5 \le x < \frac{1}{3} \\ -9x + 3 < x+5 \end{cases} \lor \begin{cases} x \ge \frac{1}{3} \\ 9x - 3 < x+5 \end{cases}
Adesso, risolviamo ogni disequazione lineare, e riportiamo i risultati:
\begin{cases} x \le -5 \\ x > 1 \end{cases} \lor \begin{cases} -5 \le x < \frac{1}{3} \\ x > -\frac{1}{5} \end{cases} \lor \begin{cases} x \ge \frac{1}{3} \\ x < 1 \end{cases}
Troviamo la soluzione di ogni singolo sistema uno per volta. Partiamo dal primo, l’intervallo comune è nessuno.
Ora il secondo, l’intervallo di soluzioni comune è:
-\frac{1}{5} < x < \frac{1}{3}
Il terzo sistema ci dà:
\frac{1}{3} \le x < 1
Uniamo adesso le soluzioni. Cioè scriviamo le soluzioni in uno schema su uno stesso rigo. Quindi otteniamo:
-\frac{1}{5} < x < 1
In questa pagina faticosa abbiamo visto come svolgere disequazioni con valore assoluto esercizi. Non solo, è stato necessario rivedere i passaggi principali e le formule usate nelle disequazioni di secondo grado e disequazioni fratte!
Trovate altre centinaia di esercizi di tantissimi altri argomenti di matematica che altro ancora!
Per approfondire le proprietà dei valori assoluti:
https://it.wikipedia.org/wiki/Valore_assoluto
Disequazioni con valore assoluto esercizi.
valore
assoluto
irrazionali
esercizi