Come trasformare un numero in logaritmo
Come trasformare un numero in logaritmo? In questa pagina vedremo che servirà una sola formula, per poter trasformare un qualsiasi numero in un logaritmo a piacere, con estrema libertà!
Indice
Iniziamo subito, la formula che vedremo sfrutta il comportamento della funzione logaritmo.
La formula da utilizzare
La funzione logaritmo è stata definita in un modo tale che possiede una particolare proprietà che sfrutteremo: se la base e l’argomento del logaritmo sono uguali, allora il logaritmo sarà uguale sempre ad uno, qualsiasi base e argomento siano.
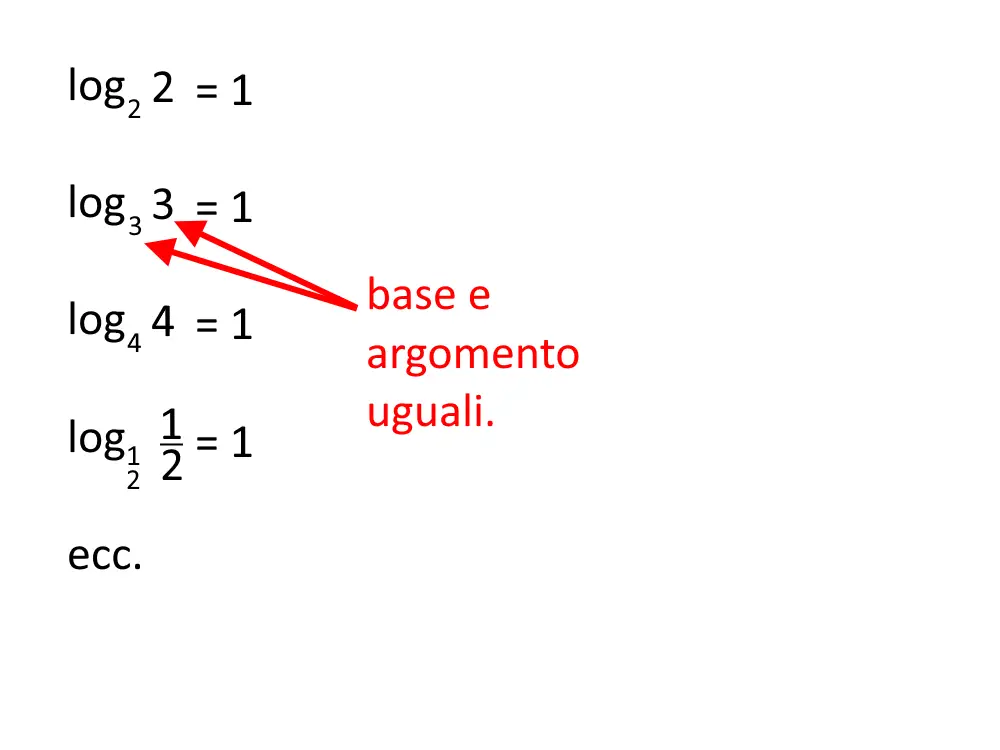
Per poter trasformare un numero in logaritmo utilizzeremo solamente questa proprietà, che vedremo negli esempi di dopo come fare.
Perché è importante?
Trasformare un numero in logaritmo è importantissimo per poter risolvere equazioni logaritmiche e disequazioni logaritmiche. Se per esempio abbiamo la seguente equazione logaritmica:
\log_3 x = 2
La risolviamo trasformando quel numero 2 in logaritmo in base 3, così mettiamo gli argomenti in uguaglianza, e risolviamo così l’equazione. Quindi questo che vedremo è un procedimento breve ma molto efficace ed utile!
Vediamo subito degli esempi su come fare!
Come trasformare un numero in logaritmo: ESEMPI
Esempio 1. Trasformare il 2 della seguente equazione in un logaritmo.
\log_3 x = 2
Prendiamo come esempio quindi proprio l’equazione di prima. Il nostro obiettivo è trasformare il 2 in un logaritmo di base 3, questo perché dobbiamo scegliere la stessa base degli altri logaritmi presenti in una equazione!
Iniziamo! Moltiplichiamo il 2 per 1:
\log_3 x = 2 \cdotp 1
Adesso, essendo che lo vogliamo in base 3, sfruttiamo la relazione seguente:
\log_3 3 = 1
Di conseguenza sostituiamo l’1 con questa relazione:
\log_3 x = 2 \log_3 3
Adesso, sfruttando la proprietà 3 dei logaritmi:
Quindi nel nostro caso quel 2 diventa l’esponente dell’argomento:
\log_3 x = \log_3 3^2
\log_3 x = \log_3 9
Ed abbiamo così trasformato quel numero 2 in un logaritmo, tra l’altro nella stessa base dell’altro nell’equazione, e quindi possiamo tranquillamente continuare l’equazione logaritmica, trovando la soluzione.
Esempio 2. Trasformare l’1 della seguente equazione in un logaritmo.
\log_2 x = 1 + \log_2 (x-2)
Come possiamo vedere, in questa equazione logaritmica ci sono tutti logaritmi in base 2, e poi c’è l’1 che ci dà fastidio perché vorremmo che fosse un logaritmo anch’esso. Questa volta non bisogna moltiplicare nulla, perché è già 1.
Visto che lo vogliamo in base 2, sfruttiamo la seguente relazione:
\log_2 2 = 1
Di conseguenza, sostituendo otteniamo:
\log_2 x = \log_2 2 + \log_2 (x-2)
Ed i giochi sono fatti!
Esempio 3. Trasformare il \frac{1}{2} della seguente equazione in un logaritmo.
\log_2 (x+1) = \frac{1}{2}
Moltiplichiamo il numero \frac{1}{2} per 1:
\log_2 (x+1) = \frac{1}{2} \cdotp 1
Essendo che vogliamo tutto in base 2, sfruttiamo la relazione:
\log_2 2 = 1
Sostituendo tale, otteniamo quindi:
\log_2 (x+1) = \frac{1}{2} \cdotp \log_2 2
Dopo di che come prima, sfruttiamo la proprietà 3 dei logaritmi, e portiamo quindi il coefficiente \frac{1}{2} come esponente dell’argomento!
\log_2 (x+1) = \log_2 2^{\frac{1}{2}}
Che poi sarebbe una radice, ossia radicale di indice 2:
\log_2 (x+1) = \log_2 \sqrt{2}
Esempio 4. Trasformare il \frac{1}{2} della seguente equazione in un logaritmo.
\log_5 (x-2) > 0,2
I numeri decimali danno sempre fastidio, quindi iniziamo a trasformare tale in una frazione:
\log_5 (x-2) > \frac{1}{5}
Dopo di che moltiplichiamo per 1 la frazione:
\log_5 (x-2) > \frac{1}{5} \cdotp 1
Come ci dice il logaritmo presenta al primo membro, vorremmo una base 5, quindi sfruttiamo la relazione:
\log_5 5 = 1
Mettiamo tale logaritmo al posto dell’1, ed otteniamo:
\log_5 (x-2) > \frac{1}{5} \log_5 5
E sfruttiamo come sempre la terza proprietà dei logaritmi, di conseguenza tale frazione diventa esponente dell’argomento:
\log_5 (x-2) > \log_5 5^{\frac{1}{5}}
Anche questa è una radice, ma di indice 5! Quando gli indici sono alti rimaniamo di solito in questa scrittura il tutto per comodità.
Ecco fatto! Non servono altri esempi perché il procedimento è sempre molto simile! E’ comunque una cosa da tenere assolutamente a mente, perché come vedete servono tanto negli esercizi per semplificarsi la vita e risolvere equazioni logaritmiche e disequazioni logaritmiche!
Trovate comunque altre centinaia di esercizi svolti e argomenti come questo, spiegati con calma, di matematica, geometria analitica e geometria!
Per approfondire:
https://it.wikipedia.org/wiki/Logaritmo
esponenziali
esercizi
logaritmiche
esercizi
