Come dimostrare che due rette sono parallele
Come dimostrare che due rette sono parallele! In questa pagina vedremo vari esercizi svolti su come si dimostra che due rette o due lati sono paralleli. Iniziamo con una piccola sezione di teoria che ci servirà, riguardo la condizione di parallelismo, poi passeremo subito a diverse tipologie di problemi ed esercizi che vi possono capitare nella verifica in classe!
Indice
Prima di iniziare gli esercizi, vediamo un secondino la teoria che ci servirà! E’ davvero poca, non preoccupatevi!
Criterio di parallelismo e
condizioni di parallelismo
Definizione di rette parallele
Partiamo col dire che siano date due rette, esse si dicono parallele se non hanno punti in comune (cioè non si toccano mai). In tal caso per scrivere che queste due rette a e b sono parallele, scriviamo: a \parallel b .
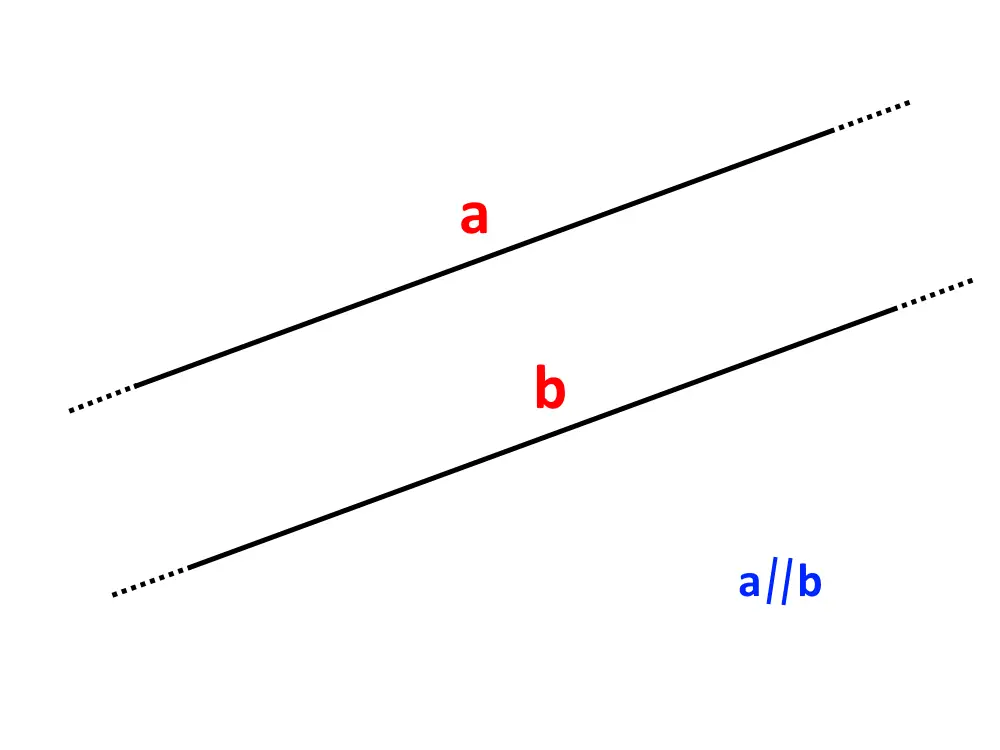
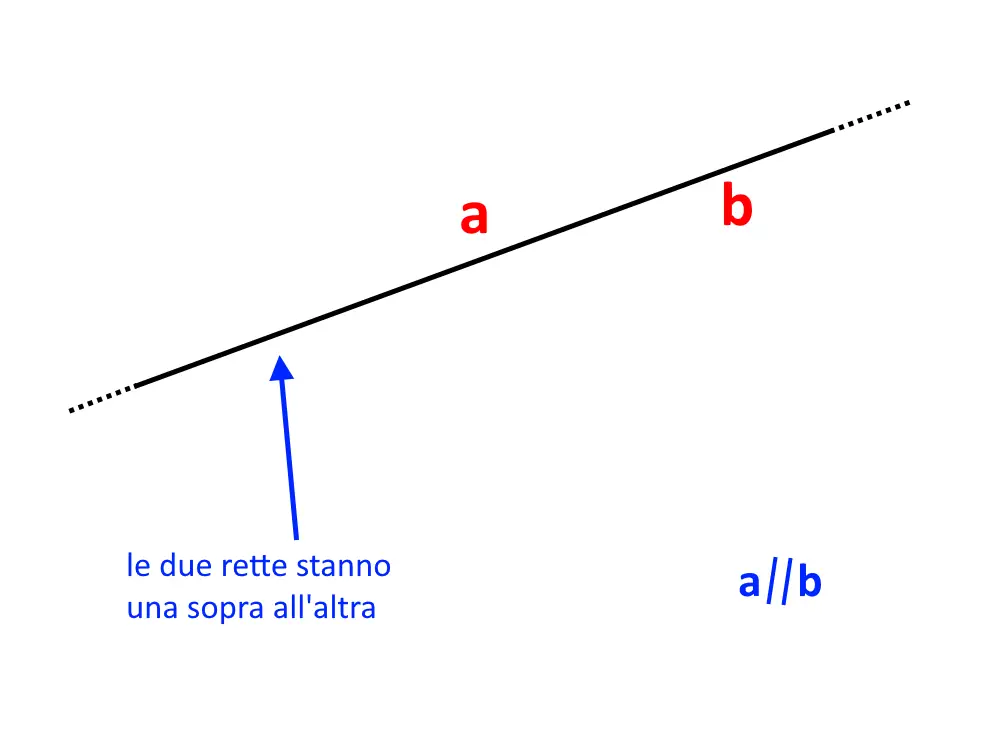
Due rette a e b si dicono parallele anche se coincidono (ossia una sta sopra l’altra in pratica).
Rette tagliate da una trasversale
Ora veniamo a cosa ci servirà negli esercizi: cioè come capire che due rette sono parallele, se queste sono tagliate da una trasversale.
Siano date due rette qualsiasi (quindi non per forza parallele) a e b, ed una terza retta c che le taglia (trasversale), come in figura.
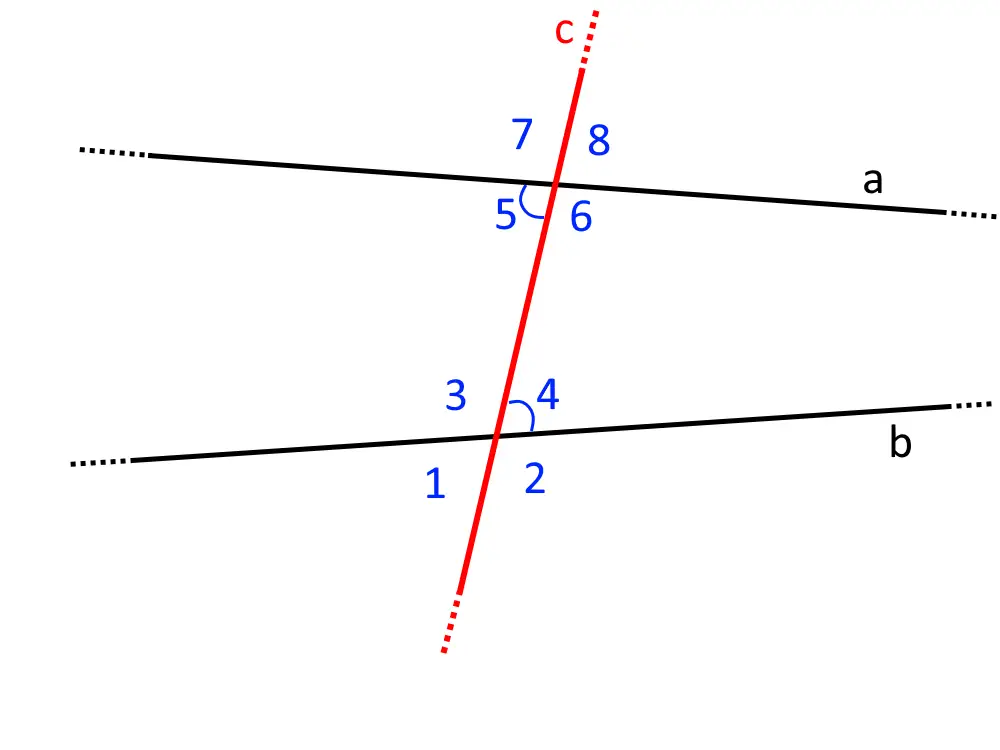
Si formano otto angoli, come vedete dalla figura. Denominiamo questi angoli con dei numeri. Chiamiamo:
- Alterni interni: gli angoli 3-6, e 4-5, ossia gli angoli che stanno all’interno, e sono opposti;
- Alterni esterni: gli angoli 1-8, e 2-7, ossia gli angoli che stanno all’esterno, e sono opposti;
- Angoli coniugati interni: gli angoli 3-5, e 4-6, ossia gli angoli che stanno dalla stessa parte all’interno;
- Angoli coniugati esterni: gli angoli 1-7, e 2-8, ossia gli angoli che stanno dalla stessa parte all’esterno;
- Angoli corrispondenti: gli angoli 1-5, 3-7, 2-6, 4-8, ossia gli angoli che stanno rispetto alla retta c nella stessa posizione (vedete il disegno per capire meglio).
A questo punto veniamo al criterio di parallelismo: la cosa più importante della pagina che ci servirà sempre in ogni esercizio!
Criterio di parallelismo
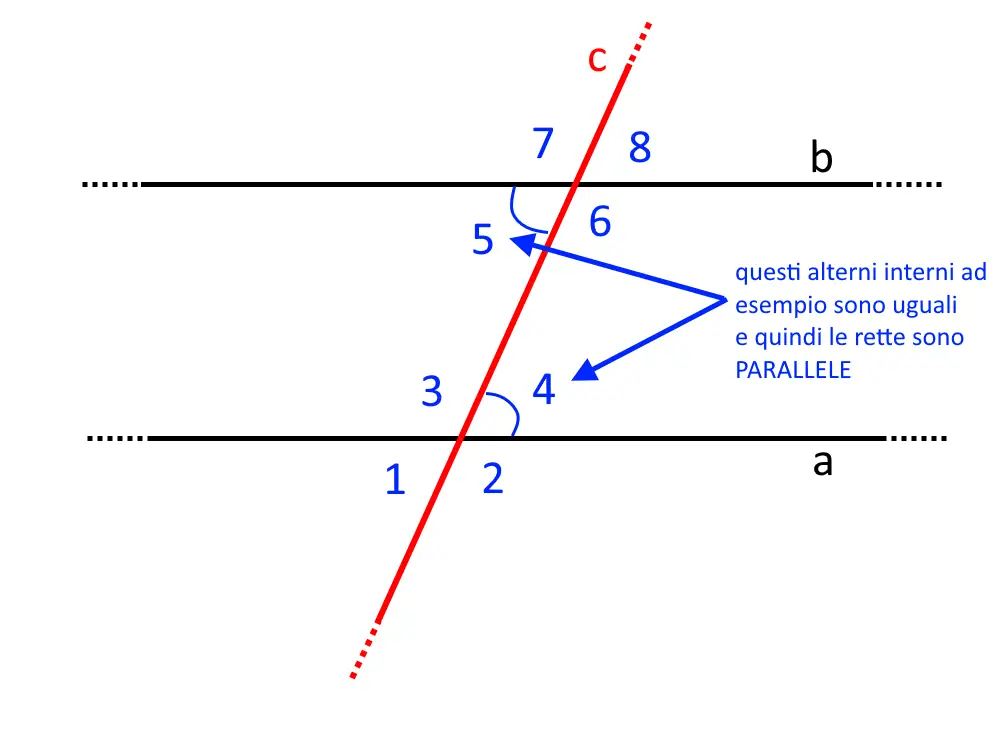
Quindi se una di queste è vera, allora ciò che avremo sarà una figura di questo tipo! Con le rette di conseguenza parallele!
Adesso che abbiamo una base forte di teoria saremo più preparati e forti per dimostrare i seguenti problemi ed esercizi!
Dimostrazione problemi sulle rette parallele
Problema 1. Consideriamo un segmento PQ e tracciamo nel suo punto medio M una retta r incidente. Fissiamo sulla retta r i punti S e T di posizione opposta rispetto a PQ, tali che MS=MT. Dimostra che la retta passante per PT sia parallela alla retta passante per QS.
Innanzitutto, inquadriamo il problema con un disegno.
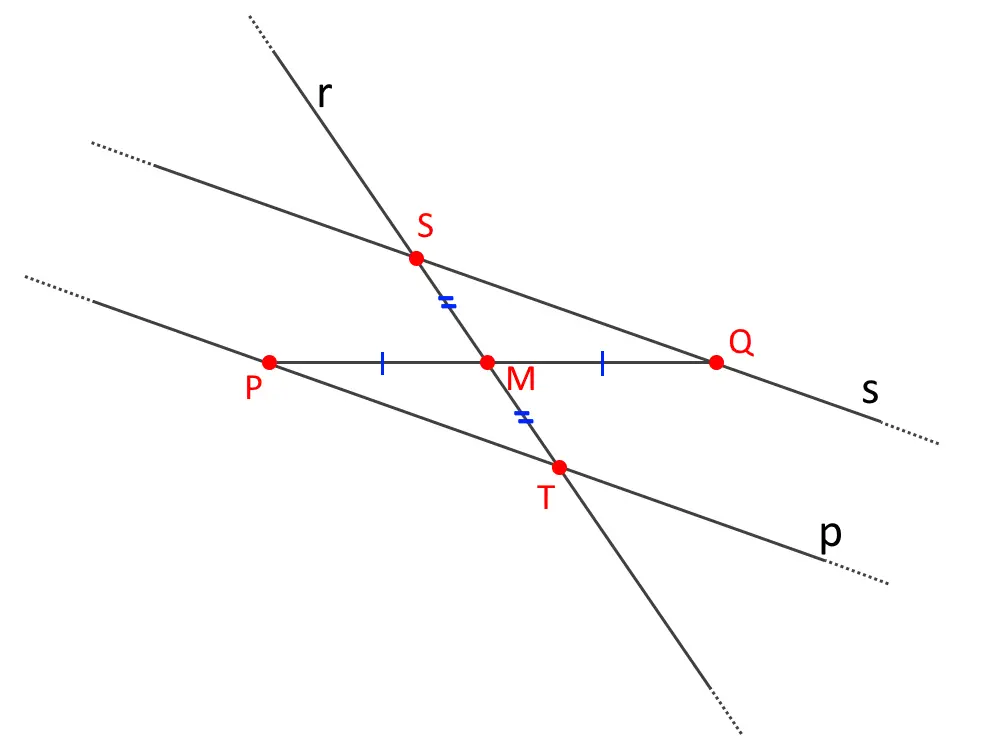
Iniziamo a discutere dei dati che ci dice il problema: esso ci parla del punto medio M del segmento PQ, di conseguenza avremo che PM=MQ. Poi notiamo inoltre che MS=MT. Indichiamo inoltre con la lettere p la retta passante per PT, e con s la retta passante per QS.
Ipotesi: \begin{cases} PM=MQ \\ MS=MT \end{cases}
Tesi: p \parallel s
Dimostrazione: Il nostro obiettivo è dimostrare che la retta p sia parallela ad s: quindi concentriamoci su queste. Notiamo fin da subito che PQ rappresenta (prolungandola) la retta trasversale che taglia le due rette p ed s. Di conseguenza siamo nel caso di due rette tagliate da una trasversale! Possiamo quindi rifarci al criterio di parallelismo! Quindi per dimostrare che le due rette sono parallele basta mostrare che, ad esempio, gli angoli alterni interni \widehat{MPT} ed \widehat{SQM} siano uguali, ed il gioco sarà fatto!
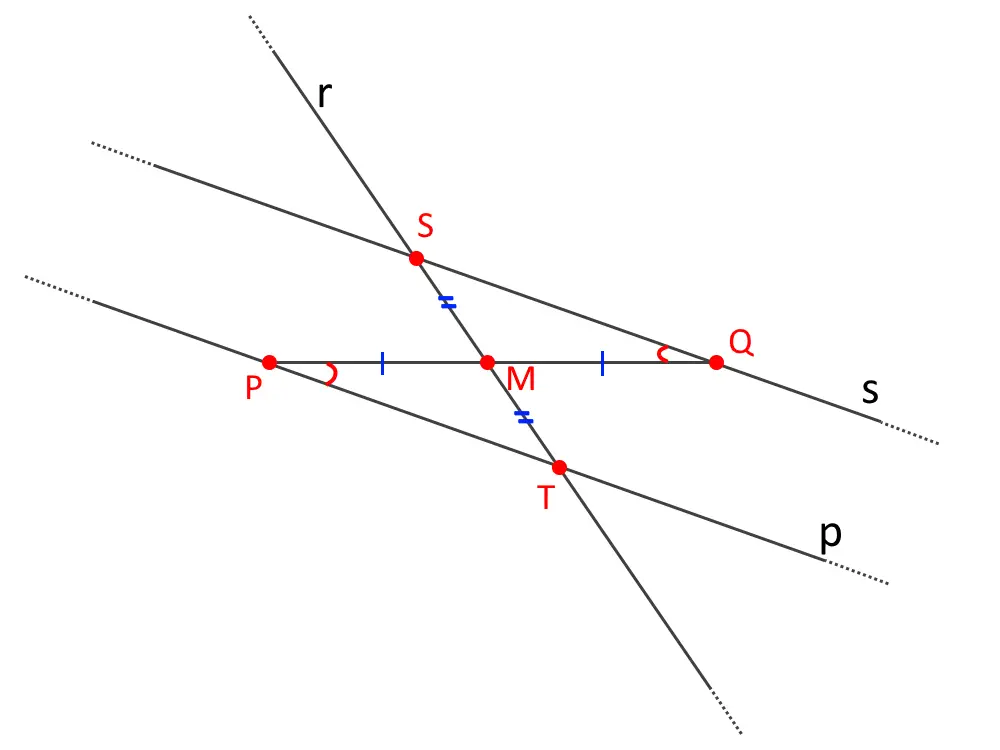
Per far ciò, consideriamo i triangoli MPT e SQM: essi hanno innanzitutto un lato uguale, dato dall’ipotesi PM=MQ. L’ipotesi ci dice anche che hanno anche un altro lato uguale MS=MT!
Notiamo inoltre che gli angoli fra essi compresi sono uguali: \widehat{PMT} e \widehat{SMQ} sono opposti al vertice!
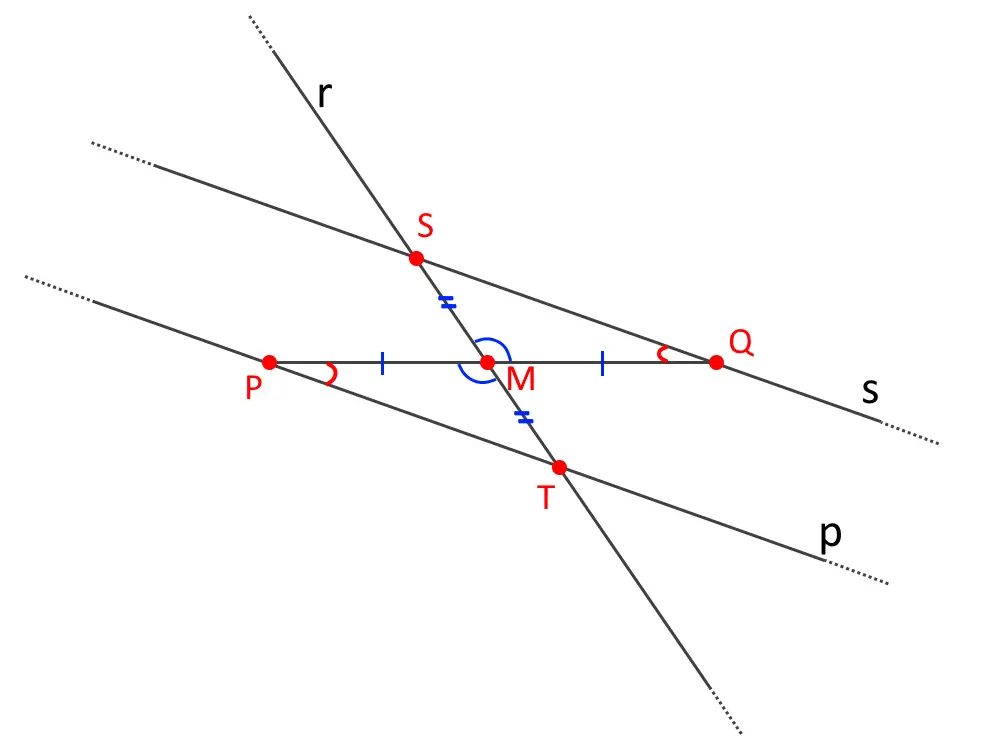
Possiamo quindi utilizzare il primo criterio di congruenza dei triangoli: due lati uguali e l’angolo fra essi compreso uguale!
Perciò i due triangoli MPT e SQM sono uguali, e di conseguenza anche tutti gli angoli all’interno!
Concludiamo perciò che quindi gli angoli \widehat{MPT} = \widehat{SQM} , e quindi vale il criterio di parallelismo: le due rette quindi sono parallele!
cvd
Vediamo un altro problema, questa volta più complicato (un classico che vi potrebbe uscire nel compito) su come dimostrare che due rette sono parallele!
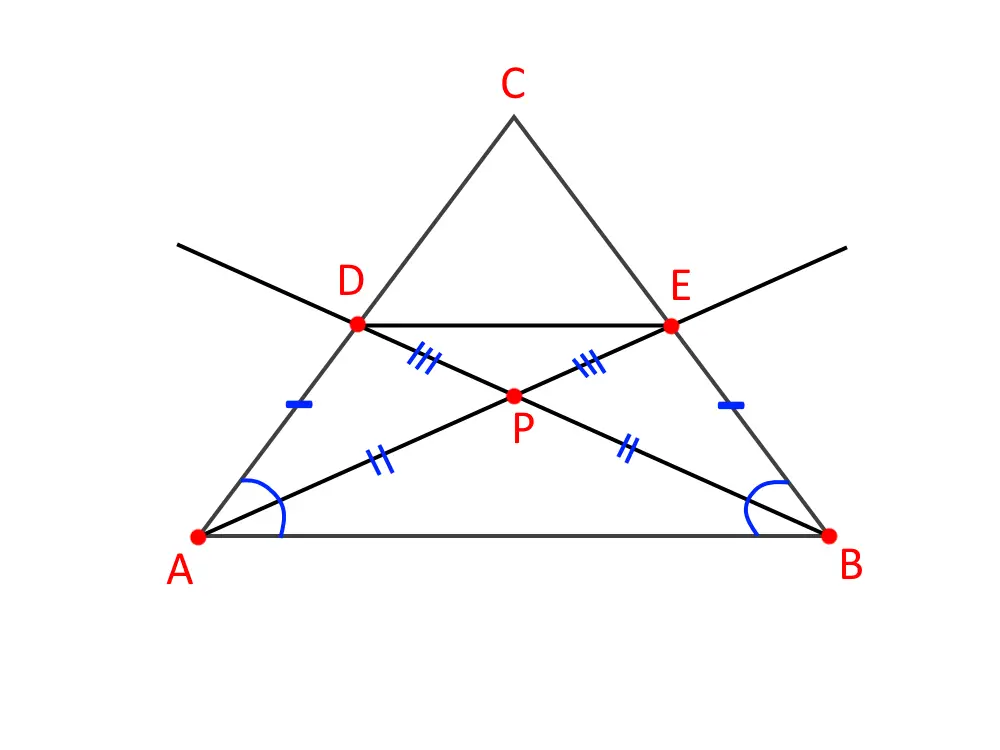
Problema 2. Consideriamo un triangolo ABC isoscele di base AB. Traccia le bisettrici AE e BD degli angoli alla base. Il punto di intersezione delle bisettrici lo indichiamo con P. Dimostra che il triangolo DEP è isoscele e dimostra che DE \parallel AB .
Come sempre, la prima cosa da fare è un bel disegno, il più preciso possibile, per non confondersi.
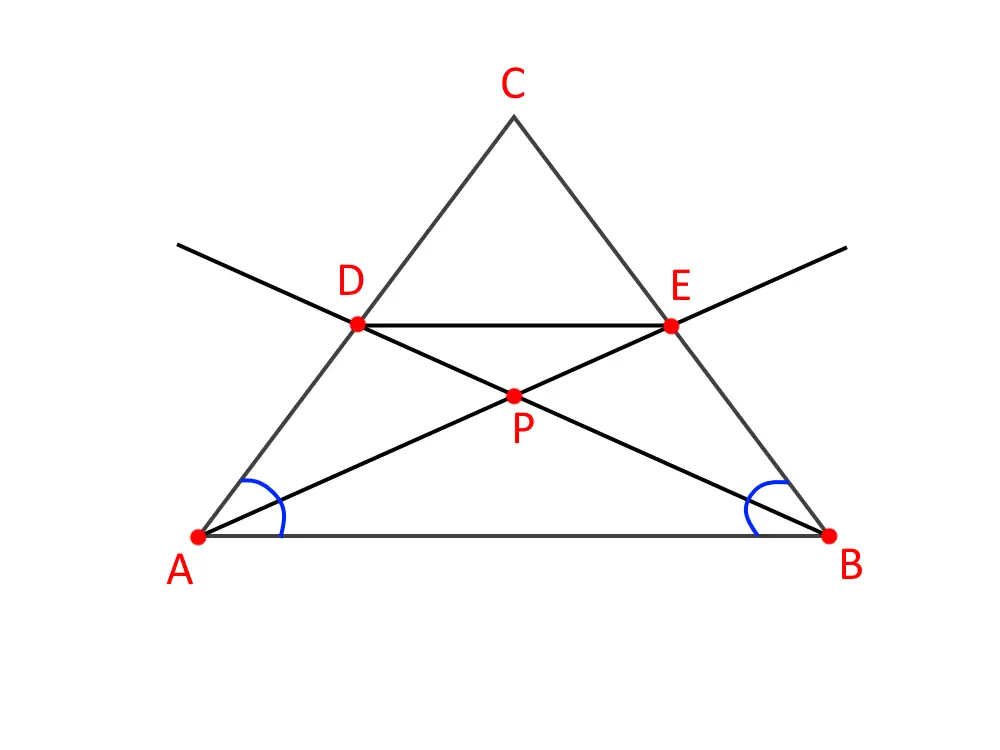
Il problema ci dice che ABC è isoscele, quindi AC=BC e gli angoli alla base sono uguali, \widehat{CAB} = \widehat{ABC} . Inoltre sappiamo che AE e BD sono bisettrici, cioè lati che tagliano l’angolo in due angoli uguali, quindi \widehat{DAP} = \widehat{PAB} e \widehat{ABP} = \widehat{PBE} . Ma poiché gli angoli alla base sono uguali, ed essi vengono tagliati a metà, allora questi quattro sono uguali fra di loro. Ossia:
\widehat{DAP} = \widehat{PAB}= \widehat{ABP}= \widehat{PBE}
Ipotesi: \begin{cases} AC=BC \\ \widehat{DAP} = \widehat{PAB}= \widehat{ABP}= \widehat{PBE} \end{cases}
Tesi: Triangolo DEP è isoscele, DE \parallel AB .
Dimostrazione: Partiamo dal primo punto, ossia cerchiamo di dimostrare che DEP è isoscele. Ricordiamo che un triangolo si dice isoscele se proviamo che ha due lati uguali, o se ha due angoli uguali.
Di conseguenza, visto che il triangolo ABP ha gli angoli alla base uguali per ipotesi, allora esso è isoscele. E quindi ha anche i due lati AP=PB uguali!
Adesso concentriamoci sui triangoli ADP e PBE, perché hanno due lati in comune col triangolo DEP che è il nostro obiettivo! Questi due triangoli hanno un lato uguale, ossia AP=PB che abbiamo appena ricavato.
Notiamo poi che questi due triangoli, per ipotesi hanno un angolo uguale:
\widehat{DAP} = \widehat{PBE}
Inoltre, anche i seguenti angoli sono opposti al vertice e quindi uguali:
\widehat{DPA} = \widehat{BPE}
Quindi i due triangoli ADP e PBE hanno due angoli e il lato fra essi compreso uguali: per il secondo criterio di congruenza dei triangoli essi sono uguali!
Essendo uguali, allora anche il lato DP=PE! Quindi, il triangolo DEP avendo due lati uguali è di conseguenza isoscele: abbiamo dimostrato il primo punto.
Passiamo al secondo: notiamo che possiamo immaginare le rette DE e AB come tagliate dalla trasversale AE ad esempio.
Per dire che DE e AB siano parallele, possiamo rifarci al criterio di parallelismo quindi, e dimostrare per esempio che gli angoli alterni interni \widehat{PAB} = \widehat{DEP} .
Abbiamo detto che il triangolo ABP è isoscele, ed ha i due angoli alla base uguali. In un triangolo la somma degli angoli è sempre 360°, allora di conseguenza è vero che:
360° = \widehat{PAB} + \widehat{ABP} + \widehat{APB}
E visto che, per ipotesi \widehat{PAB} = \widehat{ABP} allora:
360° = 2\widehat{PAB} + \widehat{APB}
E da questa ricaviamo che il primo angolo alterno interno è uguale a:
\widehat{PAB} = \frac{360° - \widehat{APB} }{2}
Ricordiamo che ciò che vogliamo dimostrare è che gli angoli alterni interni siano uguali, cioè che:
\widehat{PAB} = \widehat{DEP}
Passiamo al triangolo DEP. Anche questo è isoscele, e quindi ha due angoli uguali alla base, e facendo lo stesso discorso di prima ricaviamo che:
\widehat{DEP} = \frac{360° - \widehat{DPE} }{2}
Ma \widehat{DPE} = \widehat{APB} perché opposti al vertice! E quindi:
\widehat{DEP} = \frac{360° - \widehat{APB} }{2}
Che è esattamente lo stesso valore dell’altro angolo alterno interno! Quindi possiamo concludere che i due segmenti sono paralleli!
cvd
Abbiamo visto in questa pagina il criterio di parallelismo, e come dimostrare che due rette sono parallele ( o due segmenti). Trovate sul nostro sito centinaia di esercizi svolti di matematica ed altro ancora!
Per approfondire:
https://it.wikipedia.org/wiki/Parallelismo_(geometria)
