Quando due rette sono parallele?
Quando due rette sono parallele? Vedremo le formule che ci dicono quando due rette sono parallele, e poi faremo degli esercizi insieme, spiegati passo dopo passo. Vedremo i principali esercizi che potrebbero uscirvi nella verifica in classe. Inizieremo però con un po’ di teoria, che non fa mai male. Ma se volete potete vedere le formule, ed andare direttamente agli esercizi svolti!
Indice
Vediamo adesso le formule che utilizzeremo negli esercizi più avanti: sono due le formule.
Formule rette parallele
Consideriamo in un piano cartesiano due rette r ed s, di equazioni:
\begin{cases} r: \; y=mx + q \\ s: \; y=m'x + q' \end{cases}
Equazioni di rette scritte in questo modo si dicono in forma esplicita (cioè con la y da sola a sinistra). Se abbiamo due rette r ed s scritte in forma esplicita, diremo che queste due rette sono parallele se e soltanto se i coefficienti angolari sono uguali.
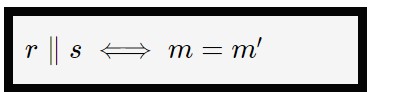
Badate bene che questa è la formula o anche condizione di parallelismo fra due rette scritte in FORMA ESPLICITA!
Adesso vediamo l’altro caso che vi può capitare: ossia di due rette scritte in forma implicita.
Consideriamo in un piano cartesiano due rette scritte in forma implicita, ossia due rette r ed s di equazioni:
\begin{cases} r: \; ax+by + c=0 \\ s: \; a'x +b'y +c' = 0 \end{cases}
In tal caso, queste due rette si diranno parallele se e soltanto se sarà verificata la seguente condizione.
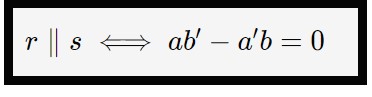
Quindi, abbiamo visto le due formule da utilizzare in caso aveste le equazioni scritte in forma esplicita, o in forma implicita.
Esse sono formule che si equivalgono. Si equivalgono perché come vedremo voi potete ricavare a vostro piacimento una della due forme. Vediamo subito come. (Questa è una sorta di dimostrazione della seconda formula, ma è utile anche per gli esercizi, quindi dategli un’occhiata).
Consideriamo una retta scritta in forma esplicita di equazione:
r: \; y=mx+q
La stessa identica retta può essere scritta anche in forma implicita, come:
r: \; ax+by+c=0
Le due forme sono equivalenti, cioè che voi scriviate una retta in una forma o nell’altra…sempre la stessa retta deve rappresentare!
Di fatti possiamo scrivere la seconda equazione isolando la y a sinistra:
by=-ax-c
Dividiamo per b:
y=-\frac{a}{b} x-\frac{c}{b}
Visto che la rappresentazione è della medesima retta r, per confronto allora deve essere che:
m= - \frac{a}{b}
Cioè abbiamo così trovato la relazione che lega i diversi coefficienti, che dicono tutti la stessa cosa alla fine, ma scritte in una maniera diversa. Stesso processo analogo possiamo fare per un’altra retta s, cui otterremmo:
m'= - \frac{a'}{b'}
Adesso utilizziamo la prima formula madre che ci dice quando due rette sono parallele:
m= m'
Sostituiamo le relazioni che abbiamo trovato:
- \frac{a}{b}= - \frac{a'}{b'}
Moltiplichiamo per bb’, e cambiamo di segno tutto:
ab'= a'b \implies ab' - a'b = 0
Ed abbiamo trovato così la seconda formula di parallelismo, che non è nient’altro che lo stesso significato della prima (di fatti siamo partiti da lì) ma scritta in funzione di coefficienti della retta in forma implicita, cioè sotto un altro linguaggio.
Se siete interessati adesso vedremo come si ricava la formula che ci dice quando due rette sono parallele, se non vi interessa passate direttamente agli esercizi!
Dimostrazione formula di parallelismo
Consideriamo in un piano cartesiano due rette r ed s parallele (quindi che non si incontrano mai). Come nella figura seguente, chiamiamo A e A’ i punti di intersezione delle rette con l’ascissa (asse x). Chiamiamo poi B e B’ i punti che distano 1 rispettivamente da A e A’, cioè stiamo dicendo che \overline{AB} = 1 e anche \overline{A'B'} = 1 .
Inoltre, segniamo come punto C e C’ la componente y relativa al punto B e B’.
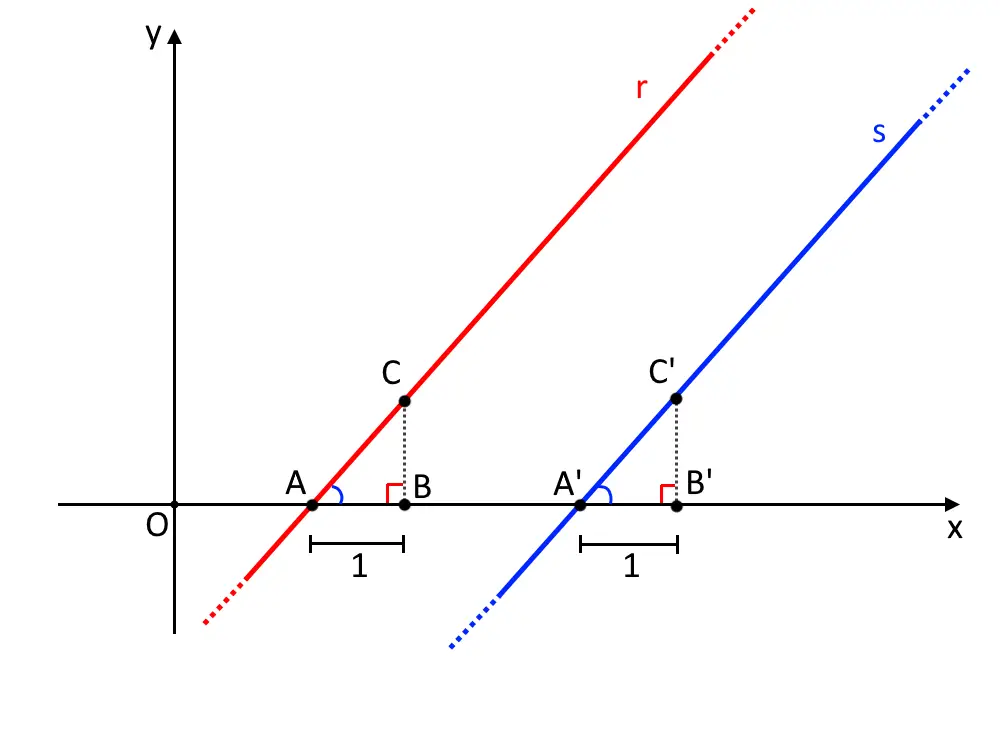
Osserviamo i due triangoli ABC e A’B’C’ : vediamo cosa hanno uguale. Hanno sicuramente un lato uguale, come detto prima, ossia:
\overline{AB} = \overline{A'B'} = 1
Inoltre, entrambi i triangoli sono rettangoli, e quindi hanno un angolo uguale di 90°.
Adesso, notiamo che le rette r ed s (parallele per ipotesi) sono tagliate dalla trasversale che è l’asse x: di conseguenza gli angoli corrispondenti \widehat{BAC} = \widehat{B'A'C'} sono uguali!
Di conseguenza i due triangoli sono esattamente uguali per il secondo criterio di congruenza dei triangoli: due angoli e il lato compreso uguali.
Essendo uguali, allora sono uguali anche i seguenti lati:
\overline{BC} = \overline{B'C'}
A questo punto richiamiamo la definizione di coefficiente angolare di una retta: il coefficiente angolare m di una retta rappresenta di quanto cresce l’ordinata di un punto rispetto alla sua ascissa. In parole povere:
m = \frac{BC}{AB} = \frac{BC}{1}
Di conseguenza ricaviamo che:
m=m'
E questa è la condizione per il quale due rette sono parallele. Per ricavare l’altra formula che abbiamo visto, basta seguire il procedimento fatto nella scorsa sezione.
Vediamo adesso la cosa più importante, esercizi svolti di diverso tipo che vi possono capitare nel compito in classe! Quindi vediamoli con calma, alcuni non sono banali, ma vi basta sapere che sono sempre gli stessi!
Come capire se due rette sono parallele
Esercizio 1. Consideriamo due rette r ed s rispettivamente di equazioni y=-2x+1 e 3y+2x+4=0. Determinare se sono parallele.
L’esercizio ci dà due rette, che scriviamo per comodità nel seguente sistema:
\begin{cases} r: \; y=-2x+1 \\ s: \; 3y+2x+4=0 \end{cases}
Come vedete però la prima è in forma esplicita e la seconda in forma implicita. Per determinare se sono parallele abbiamo bisogno che entrambe siano della stessa forma, come vedete dalle formule di parallelismo fra due rette!
In forma esplicita o implicita l’equazione rappresenta sempre la stessa retta chiaramente, sono solo due forme diverse. Decidiamo ad esempio di trasformare la seconda equazione ad esplicita, cosa che possiamo fare in pochissimi passaggi:
s: \; 3y+2x+4=0
Isoliamo la y a sinistra:
s: \; 3y=-2x-4
Dividiamo per 3:
s: \; y=-\frac{2}{3} x- \frac{4}{3}
Abbiamo così ottenuto la retta s in forma esplicita. Così abbiamo entrambe le rette in una stessa forma.
\begin{cases} r: \; y=-2x+1 \\ s: \; y=-\frac{2}{3} x- \frac{4}{3} \end{cases}
Possiamo quindi applicare la condizione di parallelismo fra due rette: cioè dobbiamo verificare l’uguaglianza della seguente formula.
m = m'
Due rette sono parallele se è verificata questa uguaglianza, ossia se il membro di sinistra è uguale a quello di destra. Nel nostro caso abbiamo:
m = m' \implies -2 = -\frac{2}{3}
Cioè chiaramente sono diversi!
-2 \ne -\frac{2}{3}
Di conseguenza le due rette NON sono parallele!
Esercizio 2. In un piano cartesiano consideriamo la retta r: y=7x+4 e la retta s passante per i punti A=(4,7) e B=(2,-7). Determinare se esse sono parallele.
Abbiamo l’equazione di una sola retta…e l’altra? L’altra sappiamo che passa per due punti, di conseguenza possiamo utilizzare la formula della retta passante per due punti per calcolare la sua equazione!
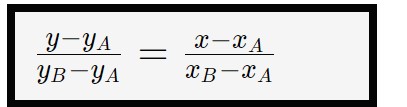
Sostituendo le componenti dei due punti ricaviamo che:
\frac{y-7}{-7-7} = \frac{x-4}{2-4}
- \frac{y-7}{14} = - \frac{x-4}{2}
Leviamo il segno meno, e moltiplichiamo tutto per 14, in modo da levare di mezzo i denominatori.
y-7 = 7(x-4)
y-7 = 7x-28
E quindi isolando la y a sinistra l’equazione della seconda retta s è, in forma quindi esplicita:
s: \; y = 7x-21
A questo punto le due rette ce l’abbiamo! Adesso non ci rimane che applicare la formula per capire se sono parallele o meno.
m=m' \implies 7=7
L’uguaglianza è verificata chiaramente e quindi questa volta le due rette SONO parallele!
Esercizio 3. Sia data la retta r: 4x+3y+2=0 ed una retta s che passa per il punto A=(-2,0). Determinare l’equazione implicita della retta s, sapendo che è parallela alla retta r.
Analizziamo cosa abbiamo: abbiamo la equazione implicita di una retta. Vogliamo conoscere l’equazione della seconda retta, dove come dati abbiamo che è parallela ad r, e passa per il punto A.
Partiamo col dato che la retta passa per un punto, quindi possiamo sfruttare la formula di una retta passante per un punto seguente.
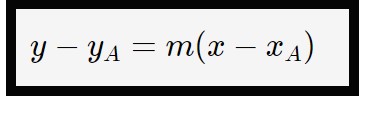
Sostituendo ai nostri dati abbiamo (mettete m’ perché riguarda la seconda retta!):
s: \; y-0 = m' (x-(-2) )
y = m' (x+2 )
Il problema ci sta dicendo che le due rette sono parallele e quindi vale:
m=m'
Il coefficiente m neanche lo conosciamo, però ce lo possiamo ricavare molto facilmente dalla prima retta, scrivendola in forma esplicita:
r: 4x+3y+2=0 \implies 3y = -4x-2
\implies y = - \frac{4}{3}x - \frac{2}{3} \implies m= - \frac{4}{3}
E di conseguenza, visto che sono parallele, allora anche:
m'= - \frac{4}{3}
Ora riprendiamo l’equazione della seconda retta:
y = m' (x+2 ) \implies y = - \frac{4}{3} (x+2 )
s: \; y = - \frac{4}{3}x - \frac{8}{3}
Abbiamo così trovato l’equazione della seconda retta…però in forma esplicita, il problema ce lo chiede in forma implicita. Per far ciò basta semplicemente portare tutto a primo membro!
s: \; \frac{4}{3}x+y+ \frac{8}{3} = 0
Per avere una forma più bella possiamo anche moltiplicare tutto per 3 se vogliamo.
s: \; 4x+3y+ 8 = 0
L’esercizio è concluso!
(Spesso questo esercizio lo portano con un risultato sbagliato sui libri)
Abbiamo visto in questa pagina degli esercizi svolti sulle retta parallele in un piano cartesiano, e quando due rette sono parallele in un piano cartesiano. Trovate altri argomenti e centinaia di esercizi svolti sia di matematica che altro ancora!
Continuate a studiare sul nostro sito!
Per approfondire:
https://it.wikipedia.org/wiki/Rette_parallele_e_perpendicolari_nel_piano_cartesiano
equazione
retta
rette sono
perpendicolari