Quando due rette sono perpendicolari?
Quando due rette sono perpendicolari? Vediamo un po’ di teoria e poi vedremo come sapere quando due rette sono perpendicolari. Cioè mostreremo da dove esce fuori la formula di perpendicolarità fra due rette, poi vedremo degli esercizi svolti e spiegati con cura.
Indice
- Formula rette perpendicolari
- Dimostrazione della formula
- Come trovare perpendicolarità fra due rette
Vediamo un pochetto di teoria, se non la conoscete ancora, per vedere come esce fuori la formula di perpendicolarità fra rette, che ci servirà molto dopo!
Formula rette perpendicolari
In un piano cartesiano, siano due rette r ed s di equazioni rispettivamente:
\begin{cases} r: \: y=mx +q \\ s: \: y=m'x +q' \end{cases}
Se le rette sono scritte in questa forma esplicita (come nel sistema di sopra), la formula che ci dirà se la retta r è perpendicolare alla retta s è la seguente.
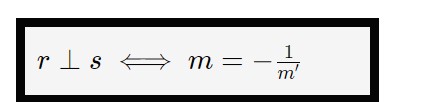
A volte può capitare che l’esercizio o il professore ci dia le equazioni della rette r ed s scritte in quest’altra forma implicita:
\begin{cases} r: \: ax+by +c=0 \\ s: \: a'x+b'y +c'=0 \end{cases}
Ed in tal caso, se avete le rette scritte in questa forma, allora la formula che vi dirà se c’è perpendicolarità fra le rette è la seguente.
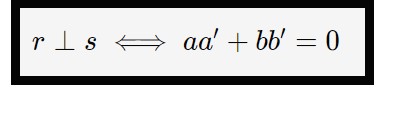
Le due formule sono equivalenti, o usate una o l’altra: dipende dall’esercizio come è proposto. E’ importante sapere che le due formule sono legate fra di loro. Di fatti una retta può essere scritta o in forma esplicita:
r: \; y=mx +q
O in forma implicita:
r: \; ax+by+c=0
Badate bene che queste due equazioni identificano la stessa identica retta, ma in un linguaggio differente.
Concentriamoci sulla seconda equazione e portiamo il termine con la y a sinistra, e tutto il resto a destra:
r: \; by=-ax -c
Dividiamo tutto per b:
r: \; y=-\frac{a}{b} x - \frac{c}{b}
Visto che questa è l’equazione sempre di r, allora deve essere uguale alla prima equazione scritta in forma esplicita:
r: \; y=mx +q
Per confronto, ricaviamo che:
m= -\frac{a}{b}
E come vedete i coefficienti sono legati fra di loro! Possiamo fare lo stesso procedimento con l’altra retta s e ricavare analogamente:
m'= -\frac{a'}{b'}
Adesso mostriamo che le due formule sono quindi equivalenti!
La prima formula di perpendicolarità ci dice che due rette sono perpendicolari se e soltanto se:
m'= - \frac{1}{m}
Sostituiamo i valori di m e m’ in funzione degli altri coefficienti:
-\frac{a'}{b'}= - \frac{1}{-\frac{a}{b}}
Portiamo la frazione di frazione sopra:
\frac{a'}{b'}= -\frac{b}{a}
Moltiplichiamo entrambi i membri per ab’ ed otteniamo così l’altra formula di perpendicolarità che abbiamo citato prima:
aa'= -bb' \implies aa' + bb' = 0
Vediamo come dimostrare adesso queste due formule (se siete interessati all’aspetto pratico andate avanti)!
Dimostrazione formula perpendicolarità
Consideriamo due rette perpendicolari r ed s (cioè che formano un angolo di 90° fra di loro), aventi per semplicità equazioni:
\begin{cases} r: \: y=mx \\ s: \: y=m'x \end{cases}
Scegliamo nel piano cartesiano il punto x=1, e tracciamo la componente y relativa alla prima retta e della seconda retta.
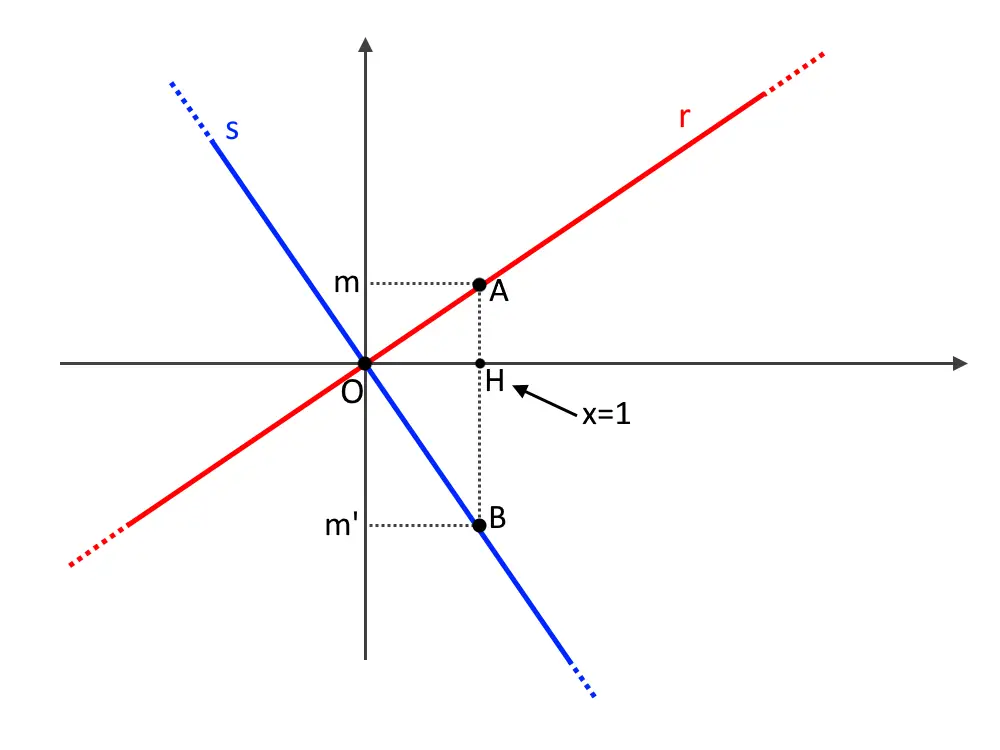
Ossia:
A=(1,mx) \implies (1,m\cdotp 1 ) \implies (1,m)
E poi segniamo anche il punto B della seconda retta s, che ha come componenti:
B=(1,m'x) \implies (1,m' \cdotp 1 ) \implies (1,m')
Notate che m ed m’ sono numeri qualsiasi, quindi possono essere anche negativi!
Applicando al triangolo ABO il secondo teorema di Euclide si ha:
\overline{OH}^2 = \overline{AH} \cdotp \overline{BH}
Visto che abbiamo scelto arbitrariamente, per la dimostrazione, il punto x=1 e OH rappresenta appunto questo, si ha chiaramente che:
\overline{OH} = 1
Inoltre:
\overline{AH} = |m|
\overline{BH} = |m'|
Notiamo che abbiamo messo i valori assoluti perché essi in questo caso rappresentano dei lati (un lato non può essere negativo) visto che abbiamo usato il teorema di Euclide. La linea sopra AH ad esempio ci dice appunto che stiamo considerando AH non come componente, ma come lato.
Dal secondo Teorema di Euclide:
\overline{OH}^2 = \overline{AH} \cdotp \overline{BH}
Segue allora che:
1 = |m| \cdotp |m'| = |m \cdotp m'|
Adesso con un ragionamento, cerchiamo di levare questo brutto valore assoluto!
Notiamo che, se due rette sono perpendicolari, se una retta risiede nel primo e terzo quadrante, l’altra per forza starà nel secondo e quarto quadrante!
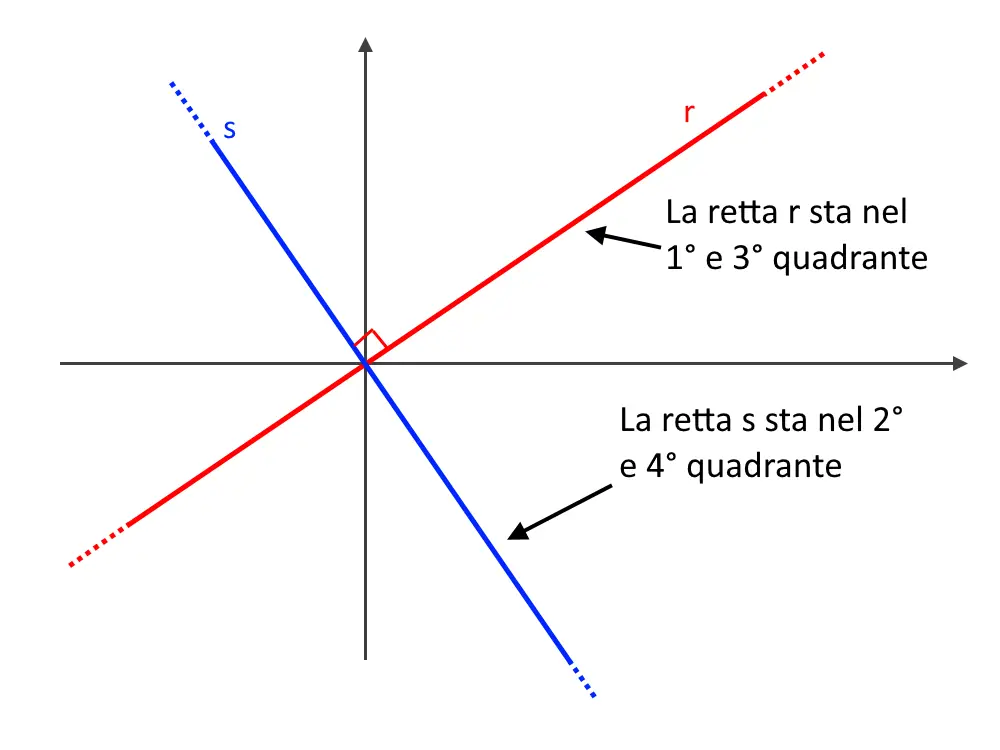
E visto che nel primo e terzo quadrante il coefficiente angolare di una retta m è sempre positivo, mentre se sta nel secondo e quarto quadrante m’ è negativo, allora il prodotto loro è negativo, e quindi:
\implies 1 = -mm' \implies m= - \frac{1}{m'}
Ed abbiamo così dimostrato la prima formula, l’altra la si trova facendo le ultime considerazioni della sezione precedente.
Nella dimostrazione, vengono considerati termini noti pari a zero, perché la perpendicolarità non li coinvolge direttamente.
Vediamo adesso degli esercizi svolti, ed esempi su come capire quando due rette sono perpendicolari!
Come trovare perpendicolarità fra due rette
Esercizio 1. Siano date le rette di equazioni r: y=3x+2 e la retta s: y=-1x, determinare se sono perpendicolari.
Per verificare la perpendicolarità di queste due rette dobbiamo utilizzare una delle due formule: in questo caso l’esercizio ci dà le equazioni delle rette in forma esplicita, quindi utilizziamo la formula seguente.
m= - \frac{1}{m'}
Cioè dobbiamo vedere se questa è vera, o in altre parole se l’uguaglianza è verificata, cioè se c’è uguaglianza fra sinistra e destra.
In questo esercizio capiamo che m=3, e che m’=-1, quindi sostituiamo nella formula:
3= - \frac{1}{-1}
3= 1
Come vedete, chiaramente 3 \ne 1 ! Quindi le due rette NON sono perpendicolari! La condizione di perpendicolarità non è stata verificata!
Esercizio 2. Sia la retta r: y=-2x-8, e sia un’altra retta s passante per i punti A=(2,1) e B=(4,2), verificare se sono perpendicolari.
La prima retta ce l’abbiamo, quindi apposto così, ci manca la seconda però. Sappiamo che la seconda retta s però passa per due punti: usiamo quindi la formula della retta passante per due punti per ricavare la sua equazione.
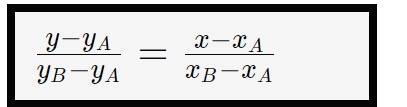
Sostituiamo in tale formula quindi le componenti dei due punti A e B, ed otteniamo:
\implies \frac{y-1}{2-1} = \frac{x-2}{4-2} \implies y-1 = \frac{x-2}{2}
Moltiplichiamo tutto per 2:
2y-2 = x-2
E adesso, per ricavare l’equazione di questa retta in forma esplicita, isoliamo la y a sinistra:
2y= x-2+2
E poi dividiamo per 2:
s: \; y= \frac{1}{2} x
Abbiamo così ricavato anche la seconda equazione della retta che ci serviva per poter applicare la condizione/formula di perpendicolarità.
m= - \frac{1}{m'} \implies -2= - \frac{1}{\frac{1}{2} }
Portiamo la frazione di frazione al di sopra:
-2=-2
Adesso l’uguaglianza è verificata e quindi le due rette sono perpendicolari fra di loro!
Esercizio 3. Sia la retta r: \; y= -x + \frac{1}{2} , calcolare l’equazione di una retta perpendicolare ad essa e passante per il punto A=(-4,-3).
Qui l’esercizio richiede un ragionamento inverso: nel senso che ci dice che ci sono due rette perpendicolari, quindi già c’è la perpendicolarità fra queste due. Ossia già vale:
m= - \frac{1}{m'}
Di conseguenza, visto che questa già vale, possiamo calcolare la formula inversa e calcolare così il coefficiente angolare m’ della seconda retta.
m'= - \frac{1}{m} = - \frac{1}{-1} = 1
A questo punto la seconda retta sarà della forma esplicita y=x + q. Ci manca cioè il termine noto. Esso lo calcoliamo dalla formula di una retta passante con coefficiente angolare per un punto.
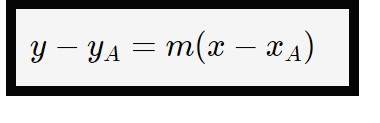
Di conseguenza nel nostro caso, che passa per A ed ha come coefficiente angolare m’=1:
y-y_A = m' (x-x_A)
y- (-3) = x- (-4)
Qui le parentesi sono importanti, attenzione!
y+ 3 = x +4
\implies s: \; y= x +1
Ed ecco trovata l’equazione della seconda retta!
In questa pagina abbiamo visto come trovare e capire quando due rette sono perpendicolari! Trovate comunque tanti altri esercizi svolti e argomenti sia di matematica che altro ancora!
Continuate a studiare sul nostro sito!
Per approfondire:
https://it.wikipedia.org/wiki/Perpendicolarit%C3%A0
rette sono
parallele?
punto di
intersezione