PARABOLA: esercizi svolti

Parabola: ESERCIZI SVOLTI! In questa pagina vedremo tutti gli esercizi svolti sulla parabola che possono uscire nella verifica in classe! Partiremo dal caso più semplice, fino a quello del caso di una retta che interseca una parabola: tutto piano piano, passo dopo passo e spiegato! Iniziamo subito e non perdiamoci in chiacchiere!

Indice

• Parabola con vertice nell’origine e asse coincidente con l’asse y
• Parabola con asse parallelo a y
• Parabola con asse parallelo a x
• Esercizi su parabola e retta

Iniziamo subito a vedere esercizi svolti parabola con vertice nell’origine e asse coincidente con l’asse y! Detto così sembra uno sciogli-lingua ma in realtà è più semplice di quello che si pensa!

---

PARABOLA con vertice nell’origine e asse coincidente con l’asse y

---

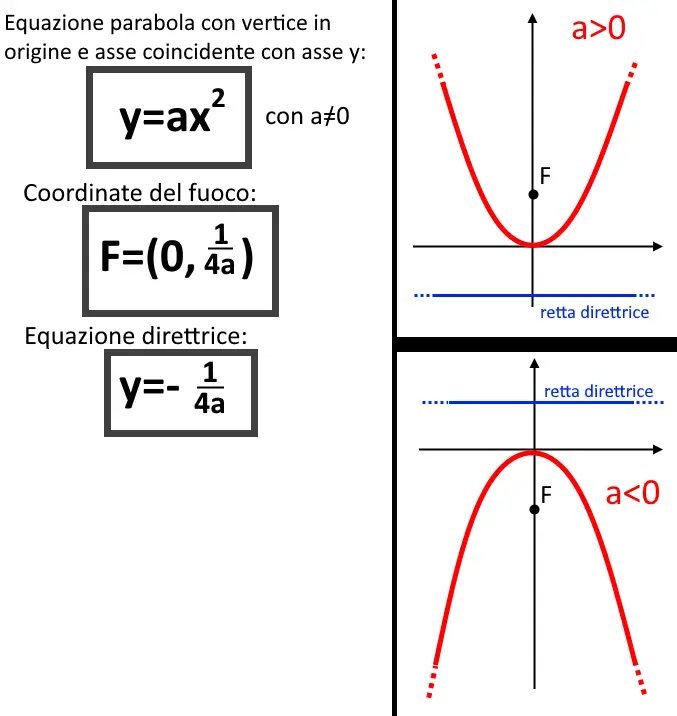
Esercizio 1. Una parabola ha il vertice V nell’origine degli assi e l’asse coincidente con l’asse y. Il fuoco è nel punto F=(0,\frac{5}{2}). Calcolare l’equazione della parabole e della direttrice.


Vediamo sopra nelle formule: l’equazione di una parabola di questo tipo è:

y=ax^2

Quindi il nostro obiettivo per calcolare l’equazione della parabola è trovare la a. Come la possiamo trovare? Vedete che la formula del fuoco contiene l’informazione della a. In particolare la formula del fuoco ci dice che:

F=(0,\frac{1}{4a})

E l’esercizio ci sta dicendo che il fuoco è:

F=(0,\frac{5}{2})

Questo significa, confrontando le due relazioni, che vale l’uguaglianza:

\frac{1}{4a} = \frac{5}{2}

E dobbiamo risolvere questa equazione per trovarci l’incognita a. Facciamo l’inverso di tutto, ossia capovolgiamo tutta l’equazione per avere la a sopra:

4a = \frac{2}{5}

Dividiamo per 4:

a = \frac{1}{10}

Abbiamo trovato la a, e quindi ora possiamo conoscere l’equazione della parabola!

y=ax^2

y=\frac{1}{10} x^2

Ora l’esercizio ci chiede di calcolare la direttrice invece. Come possiamo vedere dalle formule sopra scritte, l’equazione della direttrice ha come equazione:

y= - \frac{1}{4a}

Ma visto che a = \frac{1}{10} allora:

y= - \frac{1}{4 \frac{1}{10}} =- \frac{1}{\frac{2}{5} } =- \frac{5}{2}

L’esercizio è concluso, come vedete nulla di impossibile se si fa una cosa per volta!

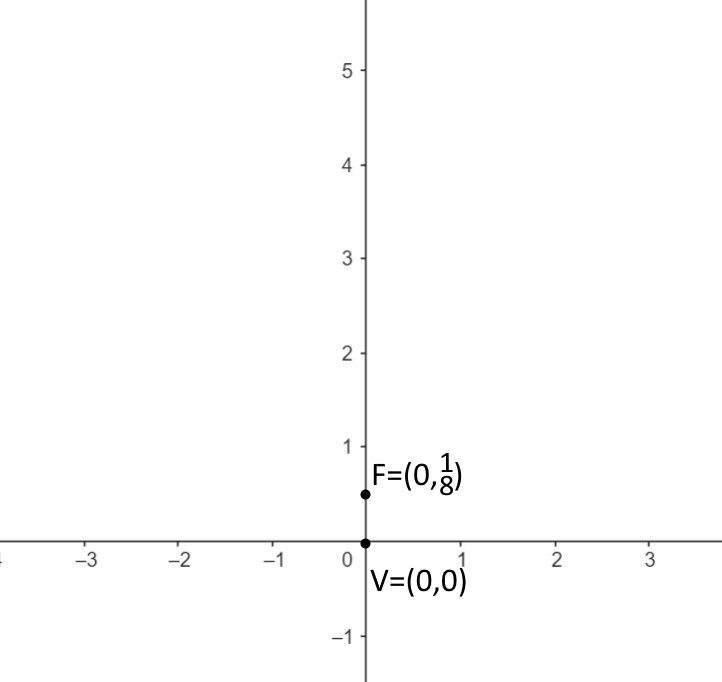
Esercizio 2. Disegna la parabola di equazione y=2 x^2


Per disegnare il grafico di una parabola di questo tipo dobbiamo seguire dei punti:

• Disegnare il vertice
• Disegnare il fuoco
• Fare una tabella dei punti x|y per vedere dove passa la parabola.

Partiamo dal primo punto: segniamo il vertice. L’equazione come vedete è della forma y=ax^2 e quindi il vertice risiede nell’origine. Troviamo le coordinate del fuoco, seguendo la formula:

F=(0,\frac{1}{4a})

Visto che l’equazione della parabola è y=2 x^2 allora significa che a=2. Quindi il fuoco ha coordinate:

F=(0,\frac{1}{8})

Segniamolo sul grafico.

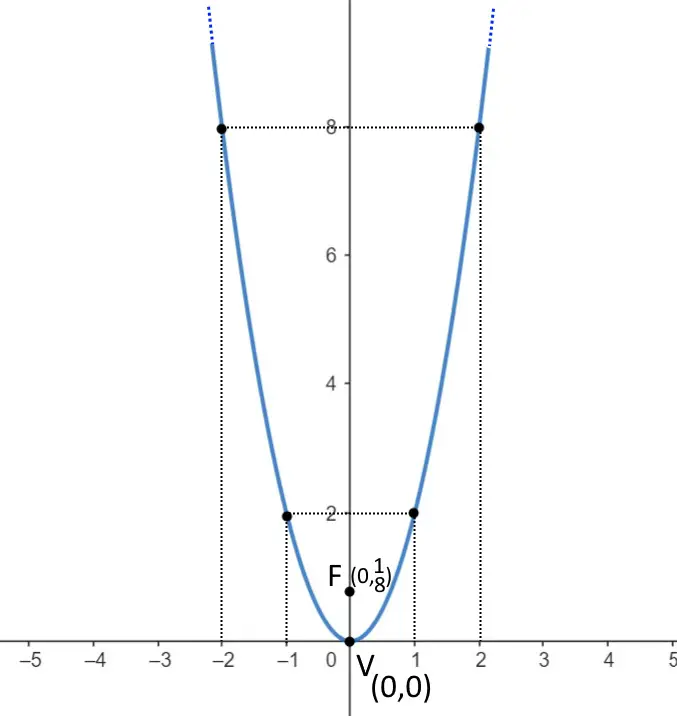
Ora ci rimane l’ultimo punto: cioè facciamo una tabella con dei valori casuali di x, al quale vi corrisponde una certa y. La y ricordate che segue la relazione y=2 x^2 . Di conseguenza se per esempio ponete x=2 allora y=2 \cdotp 2^2 =8

Segniamoci tutti questi punti sul grafico, e disegniamo la parabola che passa per questi punti.

Esercizio 3. Per quali valori di b l’equazione y= \frac{1}{b-1} x^2 rappresenta una parabola? Trova poi b, sapendo che il fuoco ha come coordinate F=(0,2) .


L’equazione di una parabola che ha come vertice l’origine, e come asse l’y, è:

y=ax^2

Nel nostro caso abbiamo:

y= \frac{1}{b-1} x^2

Per confronto quindi:

a=\frac{1}{b-1}

Abbiamo la condizione, come vedete nelle formule, che il coefficiente a \ne 0 . Il coefficiente \frac{1}{b-1} è sempre diverso da zero perché il numeratore non può annullarsi. L’unica cosa che dobbiamo fare è le condizioni di esistenza, visto che abbiamo una frazione. Le CE di una frazione vi ricordiamo essere: denominatore diverso da zero.

CE: b-1 \ne 0 \implies b \ne 1

Ora l’esercizio ci chiede di trovare b. Sappiamo che:

F=(0,2)

Sappiamo che:

F=(0,\frac{1}{4a})

E quindi per confronto otteniamo:

\frac{1}{4a} = 2

Capovolgiamo tutto ed otteniamo:

4a= \frac{1}{2} \implies a = \frac{1}{8}

Attenzione a non confondervi: il coefficiente a è diverso da b! a sarebbe tutto il numero che sta prima di x^2, cioè y=ax^2 , mentre b ne è solo una parte: cioè y= \frac{1}{b-1} x^2 !

Quindi:

\frac{1}{8} = \frac{1}{b-1}

Capovolgiamo:

8= b-1 \implies b=9

La sezione riguardo esercizi svolti parabola con vertice in origine e asse coincidente a y è conclusa. Passiamo adesso a vedere esercizi svolti di una parabola con asse parallelo a y! Quindi il vertice ora è libero!

---

Esercizi svolti PARABOLA con asse parallelo a y

Ora vediamo invece il caso di una parabola con asse parallelo a y (non più coincidente, quindi come vedete ora l’asse è cambiato), e con vertice quindi variabile! Il vertice non sta più nell’origine, ma in un punto qualsiasi del grafico.

---

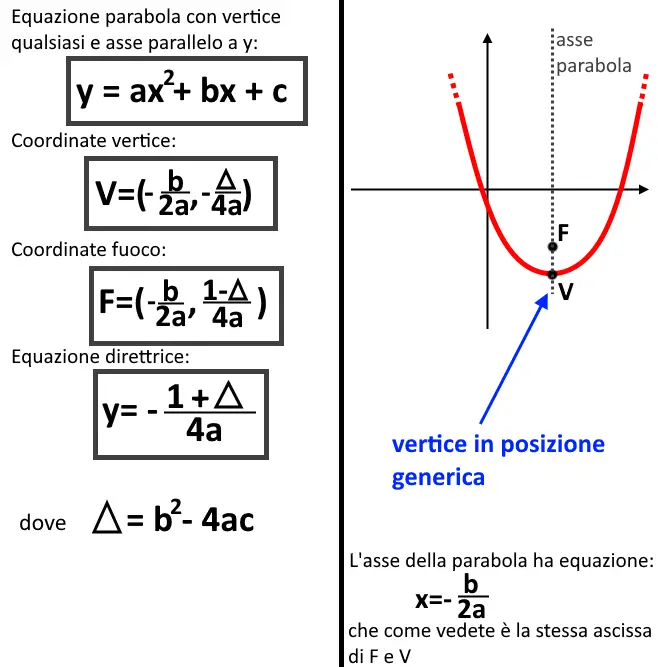
Esercizio 4. Calcolare l’equazione della parabola con asse parallelo a y, sapendo che il fuoco ha come coordinate F=(2,3) e la direttrice ha equazione y=-3.


Vi avverto già che questo tipo di parabola richiede la risoluzione di un sistema e molti calcoli, ma li faremo passo dopo passo. Partiamo semplicemente da ciò che chiede l’esercizio, ossia chiede di trovare l’equazione della parabola parallela all’asse y che, come potete vedere sopra nelle formule, ha come forma:

y = ax^2 + bx + c

Quindi come potete vedere abbiamo bisogno di trovare: a, b e c.

Se non sapete da dove iniziare, iniziate a scrivere tutto ciò che avete, ossia partiamo dalle coordinate del fuoco:

F=(- \frac{b}{2a} , \frac{1 - \Delta }{4a} )

F=(2,3)

E quindi per confronto notiamo che:

\begin{cases} - \frac{b}{2a} = 2 \\ \frac{1 - \Delta }{4a} = 3 \end{cases}

Le mettiamo in un sistema perché dobbiamo trovare più di una variabile. Ora aggiungiamo poi l’informazione che ci dà la direttrice. Di fatti dalle formule notiamo che:

y= - \frac{ 1 + \Delta }{4a}

y=-3

Per confronto allora:

- \frac{ 1 + \Delta }{4a} = -3

Cambiamo tutto di segno questa espressione, e poi mettiamola nel sistema.

\begin{cases} - \frac{b}{2a} = 2 \\ \frac{1 - \Delta }{4a} = 3 \\ \frac{ 1 + \Delta }{4a} = 3 \end{cases}

Risolviamo questo sistema per sostituzione. Notiamo che le ultime due equazioni del sistema hanno le stesse due variabili, quindi partiamo da queste. Troviamoci ad esempio dalla terza equazione il delta:

\frac{ 1 + \Delta }{4a} = 3 \implies 1 + \Delta = 12a

\implies \Delta = 12a -1

Sostituiamo questa espressione del Delta nella seconda equazione, così possiamo trovarci la a! Cioè prendiamo la seconda equazione del sistema:

\frac{ 1 - \Delta }{4a} =3

E sostituiamo il delta che abbiamo trovato:

\frac{ 1 - (12a -1 ) }{4a} =3

\frac{ 2- 12a }{4a} =3

Moltiplichiamo tutto per 4a:

2- 12a =12a \implies a= \frac{1}{12}

Ed abbiamo trovato il primo coefficiente che ci serviva!

Avendo la a, possiamo trovarci la b dalla prima equazione del sistema!

- \frac{b}{2a} = 2 \implies - \frac{b}{2\frac{1}{12}} = 2

- \frac{b}{\frac{1}{6} } = 2 \implies -6b = 2 \implies b=-\frac{1}{3}

Abbiamo trovato anche il secondo coefficiente b che ci serviva!

All’inizio avevamo ricavato che il Delta era uguale a:

\Delta = 12a -1 = 12 \frac{1}{12} - 1 = 1-1=0

Sapendo che \Delta = b^2 - 4ac allora grazie a questa possiamo trovarci la c, ultima che ci manca.

b^2 - 4ac = 0 \implies b^2 = 4ac

c= \frac{b^2}{4a} = \frac{ (-\frac{1}{3})^2 }{4\frac{1}{12}} =

c=\frac{ \frac{1}{9} }{ \frac{1}{3} } = \frac{1}{9} \cdotp 3 = \frac{1}{3}

Abbiamo tutto! L’equazione della parabola è quindi:

y= \frac{1}{12} x^2 - \frac{1}{3} x + \frac{1}{3}

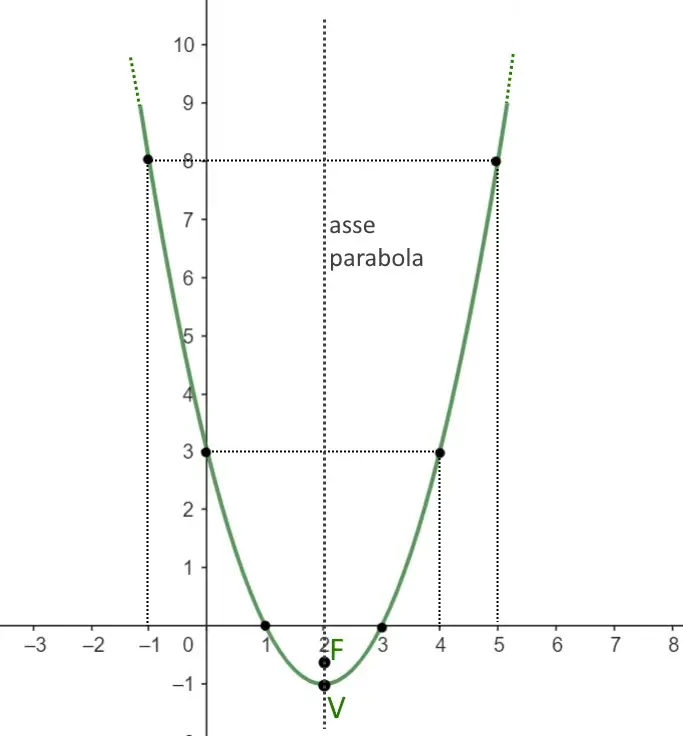
Esercizio 5. Disegna la seguente parabola y=x^2 - 4x + 3


I passaggi che si dovranno seguire per disegnare il grafico di una parabola di questo tipo, ossia con asse parallelo a y e vertice generico, sono gli stessi dell’esercizio 2. Quindi ripetiamo i passaggi principali che si dovranno andare a seguire:

• Disegnare il vertice
• Disegnare il fuoco
• Disegnare l’asse della parabola
• Fare una tabella dei punti x|y per vedere dove passa la parabola.

Partiamo col primo punto: troviamo il vertice. Le coordinate del vertice sono date da:

V= ( -\frac{b}{2a} , -\frac{\Delta }{4a} )

Dall’equazione della parabola y=x^2 - 4x + 3 capiamo quindi che:

a=1, b=-4

Calcoliamo il delta che è l’unica cosa che ci manca:

\Delta = b^2 - 4ac = 16-12=4

E quindi le coordinate del vertice sono:

V= ( -\frac{-4}{2} , -\frac{4 }{4} )

V= ( 2 , -1 )

Segniamolo sul grafico.

Troviamo adesso le coordinate del fuoco che sono date da:

F=(- \frac{b}{2a} , \frac{1 - \Delta }{4a} )

F=(- \frac{-4}{2} , \frac{1 - 4 }{4} )

E quindi F=(2 , - \frac{3 }{4} )

Segniamo anche questo punto sul grafico. Ora disegniamo poi l’asse della parabola, che è semplicemente una retta tratteggiata che passa per V ed F, tutto qui.

Ora scriviamo la tabella dei punti di x e di y per vedere dove passa precisamente la parabola, e quindi avere le informazioni necessarie per disegnarla. Come prima, scriviamo punti generici (positivi e negativi) di x e poi la y la si ricava dalla relazione y=x^2 - 4x + 3 . Quindi se per esempio imponiamo x=0 corrisponde una y=0^2 - 4\cdotp 0 + 3 =3

Scriviamo la tabella. Però per comodità: scriviamo tutte le x nei dintorni della ascissa del vertice! Ora la parabola non è più centrata su x=0 ma sul vertice che non sta più nell’origine!

Segniamo tutti questi punti sul grafico, ed otteniamo per cui la seguente parabola.

La sezione riguardo esercizi svolti parabola con vertice variabile e asse parallelo a y è conclusa. Passiamo adesso a vedere esercizi svolti di una parabola con vertice variabile e asse parallelo a x questa volta! In pratica è uguale alla sezione appena vista, ma la parabola ha formule diverse ed ha una forma ruotata, tutto qui. Quindi i procedimenti che vedremo saranno molto simili.

Esercizi svolti PARABOLA con asse parallelo a x

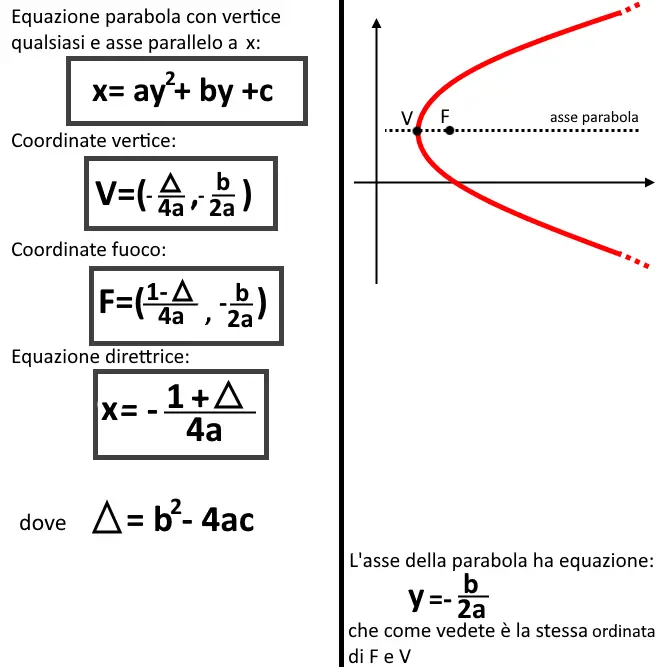
Visto che è il caso simmetricamente opposto della parabola con asse parallelo a y, le formule sono le stesse identiche ma invertite, tutto qui, come potete vedere.

---

Esercizio 6. Scrivi l’equazione della parabola che ha come fuoco F=(-1,-1) e come retta direttrice x=- \frac{3}{2} .


Dalla retta direttrice, che questa volta è x=… e non più y=…, capiamo che si tratta di una parabola con asse parallelo ad x! Lo svolgimento degli esercizi non cambia da quelli precedenti. Bisogna solo seguire formule invertite. L’esercizio ci chiede l’equazione della parabola che è della forma:

x = a y^2 + by + c

Quindi ci servono a,b e c. Ce li troviamo dalle informazioni che abbiamo: ossia mettendo a sistema le coordinate del fuoco e l’equazione della direttrice. Di fatti sapendo che:

\begin{cases} x_F = \frac{ 1 - \Delta }{4a} \\ y_F = -\frac{b}{2a} \\ x= - \frac{ 1 + \Delta }{4a} \end{cases}

Sostituiamo i dati che il problema ci dà:

\begin{cases} -1 = \frac{ 1 - \Delta }{4a} \\ -1 = -\frac{b}{2a} \\ - \frac{3}{2} = - \frac{ 1 + \Delta }{4a} \end{cases}

Il nostro obiettivo ricordiamo, è trovare a,b e c. Risolviamo il sistema per sostituzione. Notiamo che la prima e la terza equazione del sistema hanno le stesse variabili, quindi ricaviamo dalla prima equazione una variabile: ad esempio la Delta.

-1 = \frac{ 1 - \Delta }{4a}

Moltiplichiamo tutto per 4a:

-4a = 1 - \Delta \implies \Delta = 1+4a

Ora che abbiamo trovato il delta in funzione di a, la sostituiamo nella terza equazione (perché le variabili sono le stesse):

- \frac{3}{2} = - \frac{ 1 + \Delta }{4a}

E quindi, sostituendo la relazione trovata del delta:

- \frac{3}{2} = - \frac{ 1 +1+4a }{4a}

- \frac{3}{2} = - \frac{ 2+4a }{4a}

Moltiplichiamo tutto per 4a:

- 6a = -( 2+4a )

- 6a = -2-4a \implies a = 1

Abbiamo così trovato la prima lettera, ora ricaviamo le altre. Notiamo che, avendo a, dalla seconda equazione possiamo ricavarci direttamente b:

-1 = -\frac{b}{2a}

Però ora abbiamo la a e quindi:

-1 = -\frac{b}{2}

-2 = -b \implies b=2

Ed abbiamo così anche ricavato la seconda lettera! Ci manca solo la c: riprendiamo la relazione del delta ricavata all’inizio dei calcoli.

\Delta = 1+4a

\Delta = 1+4 \cdotp 1 = 5

Ricordiamoci che il delta è uguale a:

\Delta = b^2 - 4ac = 5

b^2 - 4ac = 5

Sostituiamo i valori di a e b che abbiamo:

2^2 - 4c = 5

4 - 4c = 5

E quindi:

- 4c = 1 \implies c = - \frac{1}{4}

Abbiamo tutto per scrivere l’equazione della parabola! Essa è:

x = y^2 +2y - \frac{1}{4}

---

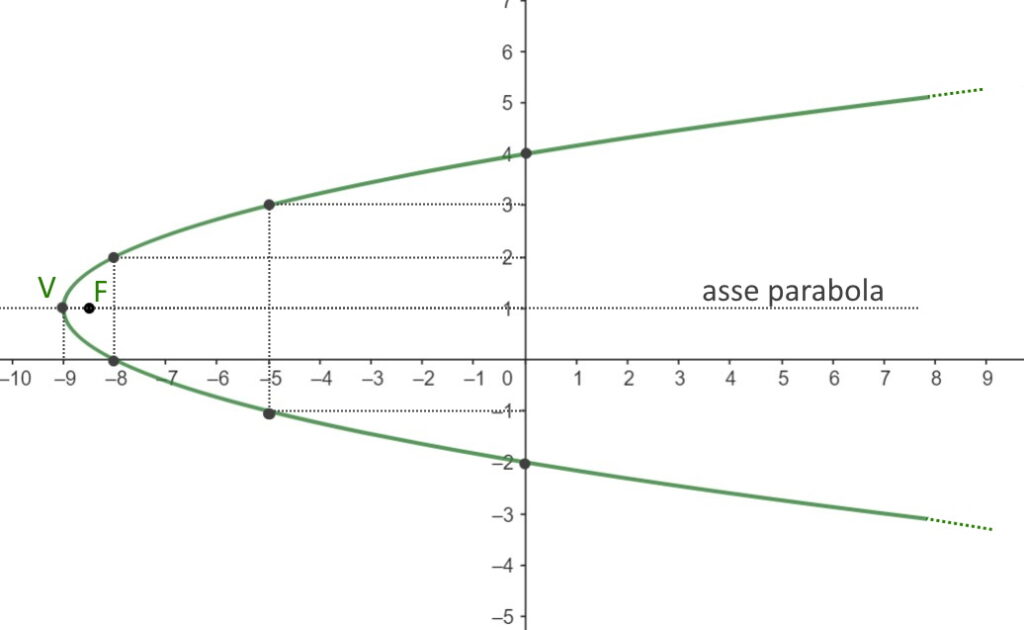
Esercizio 7. Disegnare la parabola avente equazione x-y^2 +2y + 8 = 0


Innanzitutto isoliamo la x a primo membro e portiamo tutto il resto a secondo membro, così abbiamo la forma classica della parabola:

x=y^2 -2y - 8

Come possiamo vedere la forma è quella di una parabola parallela all’asse x. Il procedimento è analogo agli esercizi di grafici precedenti. L’unica accortezza sta nella tabella y|x alla fine, che ora è invertita. I passaggi sono:

• Disegnare il vertice
• Disegnare il fuoco
• Disegnare l’asse della parabola
• Fare una tabella dei punti y|x per vedere dove passa la parabola.

Iniziamo a trovare le coordinate del vertice che sono:

V= (- \frac{\Delta}{4a} , - \frac{b}{2a} )

Dall’equazione della parabola che ci dà il problema capiamo che:

a=1, b=-2, c=-8

Mentre il delta:

\Delta = b^2 - 4ac = 4+32=36

Di conseguenza le coordinate del vertice sono:

V= (- \frac{\Delta}{4a} , - \frac{b}{2a} ) = (- \frac{36}{4} , - \frac{-2}{2} )

E cioè:

V= (- 9 , 1)

Segniamolo sul grafico. Poi passiamo alle coordinate del fuoco:

F= ( \frac{ 1 - \Delta }{4a} , - \frac{b}{2a} ) = ( \frac{ 1 - 36 }{4} , 1 )

E cioè:

F = ( - \frac{ 35 }{4} , 1 )

Segniamo anche questo sul grafico, ed andiamo a segnare anche l’asse della parabola, che sarebbe semplicemente una retta che passa per V ed F! Passiamo ora alla tabella: qui c’è da fare attenzione perché la tabella ora è invertita, cioè abbiamo prima y con valori intorno alla y del vertice (y=1) e poi dopo la x!

Segniamo sul grafico tutti questi punti e siamo pronti per disegnare la parabola!

La sezione riguardante esercizi svolti parabola con asse parallelo a x è conclusa. Passiamo alla sezione successiva, che tratterà della retta e della parabola.

---

Esercizi svolti RETTA e PARABOLA

Vediamo in breve i passaggi che effettueremo in questi esercizi riguardante la posizione di una retta rispetto alla parabola!

---

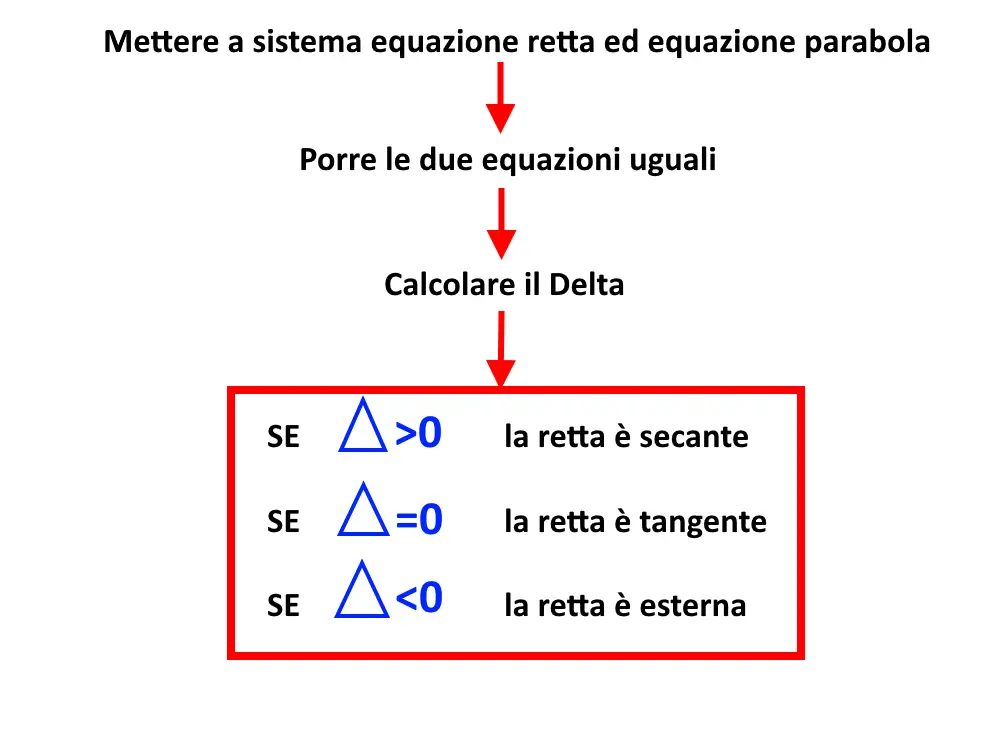
Esercizio 8. Determinare, se esistono, i punti di intersezione della retta di equazione y=-x con la parabola di equazione y=x^2 - x -1 . Determinare inoltre se la retta è secante, tangente o esterna.


Iniziamo col primo punto: mettere a sistema l’equazione della retta con l’equazione della parabola.

\begin{cases} y=-x \\ y=x^2 - x -1 \end{cases}

Poniamo in uguaglianza, col metodo del confronto, le due equazioni:

-x = x^2 - x -1

Ed ora terzo punto: troviamo il delta dell’equazione di secondo grado che è uscita fuori. Per prima cosa portiamo tutto a primo membro:

-x^2 + x +1 -x = 0

-x^2 +1 = 0

Ora, visto che nelle equazioni di secondo grado vogliamo sempre il coefficiente a (cioè il primo) positivo, cambiamo di segno:

x^2 -1 = 0

Adesso ricordandoci la forma generale di una equazione di secondo grado, ossia:

ax^2 +bx + c = 0

Calcoliamo il delta:

\Delta= b^2 - 4ac = 0^2 - 4 \cdotp 1 \cdotp (-1) = 4

Nel nostro caso come potete vedere il coefficiente b=0. Vedendo nella tabella, notiamo che essendo delta>0 significa che abbiamo che la retta è secante. Secante significa che la interseca in 2 punti. Dobbiamo adesso calcolare i punti di intersezione. Per farlo, calcoliamo un attimo le soluzioni dell’equazione di secondo grado:

x^2 -1 = 0 \implies x^2 = 1 \implies x= \pm 1

Adesso, mettiamo a sistema una soluzione x per volta con l’equazione della retta:

\begin{cases} y=-x \\ x=1 \end{cases} \implies \begin{cases} y=-1 \\ x=1 \end{cases}

dove si è sostituito il valore della x=1 alla prima equazione: abbiamo così ricavato il primo punto di intersezione fra retta e parabola. Adesso facciamo la stessa cosa con l’altro punto x=-1:

\begin{cases} y=-x \\ x=-1 \end{cases} \implies \begin{cases} y=1 \\ x=-1 \end{cases}

Quindi la retta è secante la parabola, e i due punti di intersezione sono (1,-1) e (-1,1).

---

Esercizio 9. Determinare i punti di intersezione della retta di equazione y=2x+5 con la parabola di equazione y=x^2 +2x + 5 . Disegnare inoltre il grafico della retta e della parabola.


Partiamo dal determinare i punti di intersezione, se ci sono. Quindi mettiamo a sistema le due equazioni:

\begin{cases} y=2x+5 \\ y=x^2 +2x + 5 \end{cases}

Mettiamole in uguaglianza, mettendole a confronto:

2x+5=x^2 +2x + 5

Portiamo tutto a primo membro questa equazione di secondo grado:

2x+5-x^2 -2x - 5 = 0

-x^2 = 0

Cambiamo di segno:

x^2 = 0

Calcoliamo il delta:

\Delta = b^2 - 4ac = 0 - 4\cdotp 1 \cdotp 0 = 0

E di conseguenza essendo Delta=0 la retta è tangente alla parabola in un solo punto. Vediamo quale: calcoliamo la x dall’equazione:

x^2 = 0 \implies x=0

Il punto di intersezione avviene quindi in x=0, vediamo a quale y corrispondente. Mettiamo a sistema l’equazione della retta con x=0:

\begin{cases} y=2x+5 \\ x=0 \end{cases} \implies \begin{cases} y=5 \\ x=0 \end{cases}

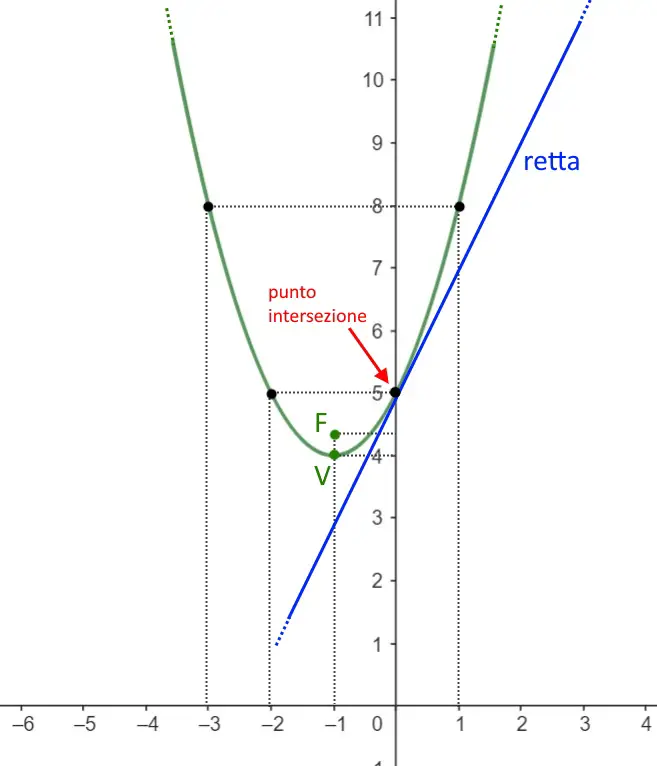
Il punto (0,5) è di intersezione. La retta è tangente la parabola.

Ora il problema ci chiede di graficare il tutto. Il grafico della parabola (come vedete è asse parallelo a y) lo sappiamo fare, e quindi dobbiamo calcolare per prima cosa il vertice.

Essendo che la parabola è: y=x^2 +2x + 5

V= ( -\frac{b}{2a} , -\frac{\Delta }{4a} ) = ( -1 , -\frac{\Delta }{4} )

Dove il Delta della PARABOLA (quello di prima era il delta della retta attenzione a non confondervi) è:

\Delta = b^2 - 4ac = 4-20=-16

E di conseguenza il vertice ha coordinate:

V = ( -1 , 4 )

Troviamo il fuoco:

F=(- \frac{b}{2a} , \frac{1 - \Delta }{4a} ) = (- 1 , \frac{17 }{4} )

Disegniamo l’asse della parabola che sarebbe una retta tratteggiata che passa per V ed F. Poi troviamo alcuni punti (negli intorni di x=-1) della parabola per disegnarla.

Disegniamo la parabola passante per i suoi punti. Poi ci rimane da disegnare la retta, qui sapendo che è tangente al punto (0,5) possiamo semplicemente disegnare una retta che taglia tale punto della parabola.

---

In questa pagina abbiamo visto esercizi svolti parabole con vertice nell’origine, asse parallelo a y e parallelo a x, ed infine abbiamo visto esercizi svolti con una retta che interseca una parabola.

Potete continuare a studiare sul nostro sito: dove trovate centinaia di altri esercizi svolti su argomenti sia di matematica che altro ancora!

Per approfondire:
https://it.wikipedia.org/wiki/Parabola_(geometria)


Parabola esercizi svolti

Direttrice
parabola

Iperbole
formule