Iperbole: equazione, esempi svolti e spiegati e formule

In questa pagina vedremo la definizione di iperbole, le diverse equazioni nei suoi diversi tipi, poi le formule di fuochi e vertici, poi formule degli asintoti, ed alla fine vedremo esempi di esercizi svolti e spiegati con cura, passo dopo passo.

Indice

• Iperbole con fuochi sull’asse x
• Iperbole con fuochi sull’asse y
• Iperbole equilatera
• Esempi svolti e spiegati

Esistono più varianti diverse di iperboli: iperbole che ha i fuochi sull’asse x, iperbole che ha i fuochi sull’asse y ed iperbole equilatera. Per questo le tratterremo separatamente una alla volta. Cominciamo subito!

---

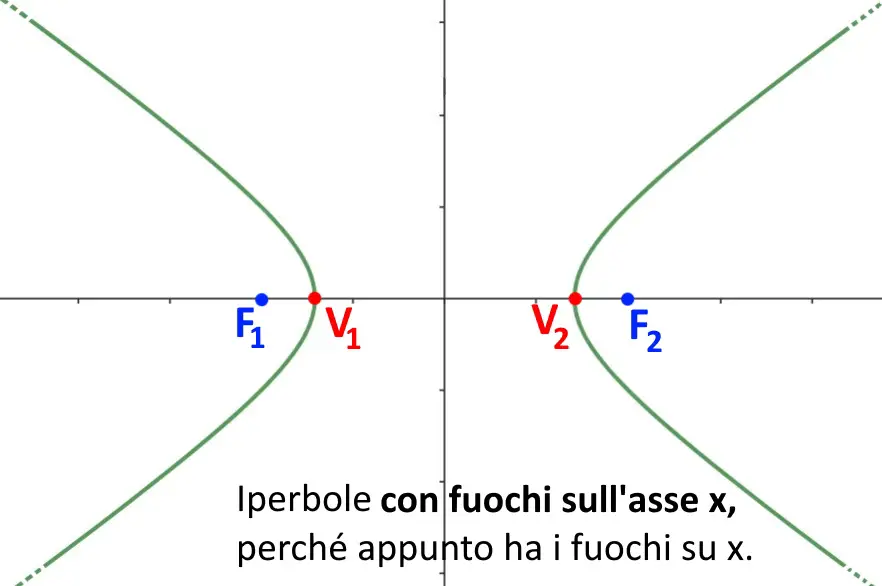
Iperbole con fuochi sull’asse x

Visto che questo è il primo tipo di iperbole che trattiamo, la spieghiamo anche più approfonditamente, facendovi capire tutte le caratteristiche di un iperbole. Non entreremo in dettaglio di cose come ” l’iperbole è il luogo geometrico…blablabla ” ma vediamo direttamente le sue equazioni, capiamo le sue formule e siamo pronti per gli esercizi! Partiamo dalla sua equazione!

---

Equazione dell’iperbole con fuochi sull’asse x

Un iperbole è una figura geometrica che viene identificata nel piano cartesiano grazie alla conoscenza della sua equazione. L’equazione che rappresenta un iperbole ha la forma seguente.

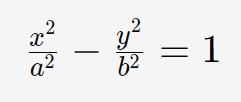
Poiché vi sono vari tipi di iperboli, dobbiamo specificare alcune cose. Questa equazione è riferita ad un iperbole che ha i suoi fuochi e i vertici sull’asse x (nella sezione successiva capiamo cosa sono i fuochi ed i vertici).

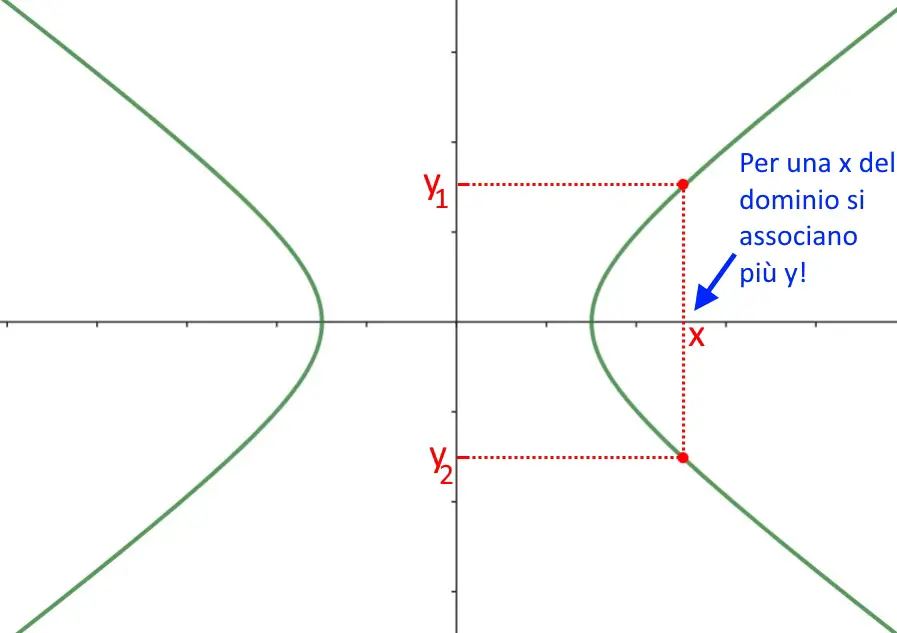
L’equazione dell’iperbole non rappresenta una funzione! Prima abbiamo detto che un iperbole è una figura geometrica, e l’abbiamo fatto perché bisogna tenere bene in mente una cosa: un iperbole non è una funzione. Questo perché per una particolare x del dominio vi si associano più valori del codominio y. Ma questo non ci darà fastidio negli esercizi, è solo bene saperlo!

Abbiamo detto che la precedente equazione rappresenta un iperbole che ha i fuochi ed i vertici sull’asse x. Cosa sono precisamente e come si calcolano?

Cosa sono i fuochi ed i vertici di un iperbole e come si calcolano

Cerchiamo di essere brevi ed efficaci: un vertice è un “estremo interno” di un iperbole, cioè dove “nasce” l’iperbole. E’ il punto più interno di un iperbole. E’ il punto dove il grafico inizia a cambiare direzione…insomma ci siamo capiti!

Per il fuoco, o meglio i fuochi, invece bisognerebbe fare un discorso più puramente geometrico, parlando di luogo geometrico ecc. Vi basti sapere che i fuochi stanno nella stessa direzione dei vertici, ma posizionati un po’ più esternamente.

Ora che abbiamo capito cosa sono, come si calcolano e come si trovano? Per trovare il posizionamento di fuochi e di vertici (cosa importante per fare poi il grafico), bisogna conoscere l’equazione dell’iperbole. Ossia conoscendo:

\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1

Grazie alla conoscenza di questa equazione, possiamo calcolare i fuochi ed i vertici con le seguenti formule.

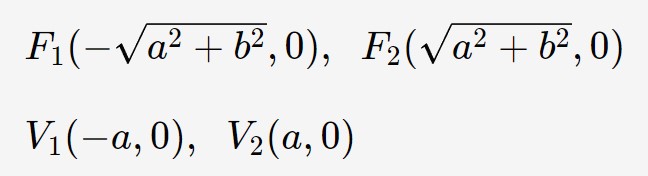
Potete notare che la componente della y è sempre 0, proprio perché questa è un iperbole “che ha fuochi sull’asse x”!

Adesso che abbiamo capito anche come trovare i fuochi ed i vertici, per disegnare un iperbole e capire come è fatta, bisogna fare un altro step: calcolare i suoi asintoti.

---

Asintoti dell’iperbole con fuochi sull’asse x

Per questa piccola sezione, super importante soprattutto per gli esercizi di grafici, ci abbiamo dedicato un’intera pagina: asintoti dell’iperbole, che vi invito a cliccare. Quindi qui riassumerò brevemente ciò che è stato detto lì. Quindi se qualcosa non vi sarà chiaro, sappiate che troverete la risposta in quella pagina.

Un iperbole possiede degli asintoti: cosa sono? Un asintoto è una linea retta immaginaria. L’iperbole infatti ad un certo punto (agli estremi destra e sinistra) segue una direzione ben precisa come vedete.

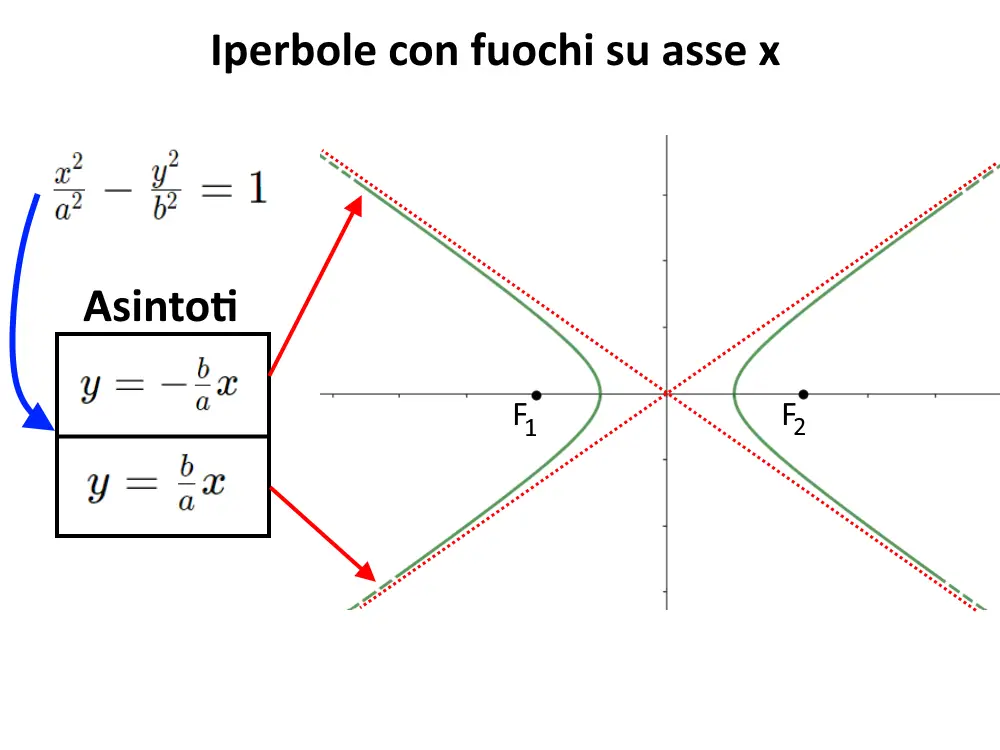
Questo è dovuto alla presenza di asintoti, detti obliqui (perché obliqui appunto). Una caratteristica è che: un asintoto non tocca mai il grafico dell’iperbole. Cioè i due si avvicinano sempre di più ma non si toccano mai.

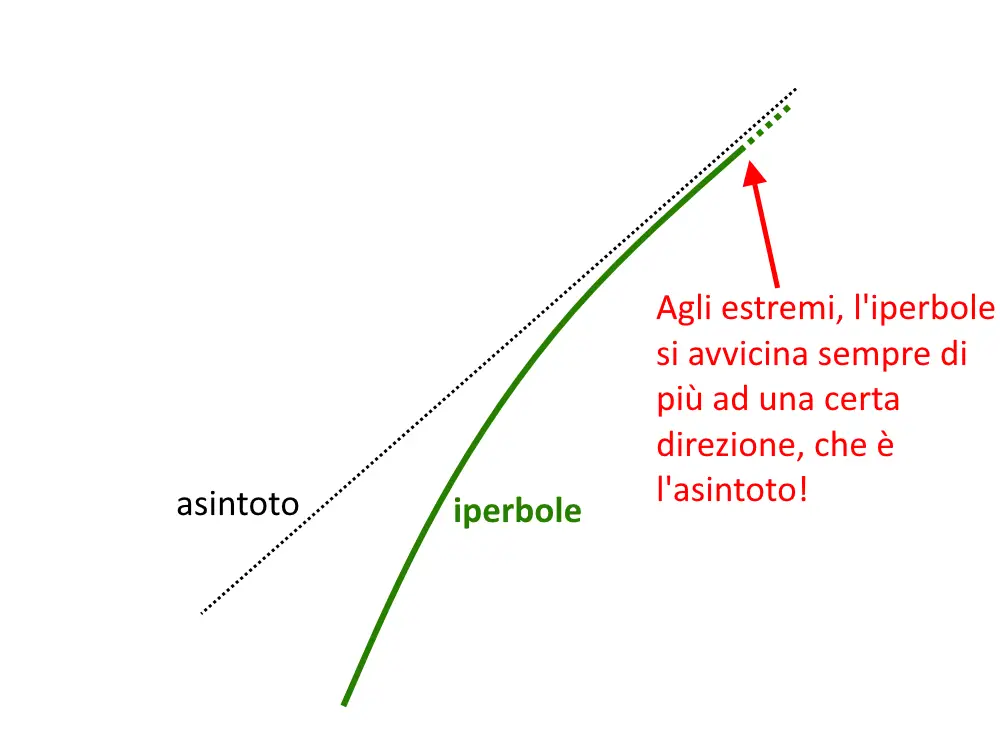
Non sottovalutate questa sezione perché è fondamentale per disegnare un iperbole! Vediamo adesso come calcolare gli asintoti. Le formule degli asintoti sono le seguenti.

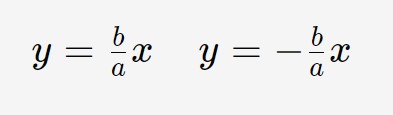
Possiamo notare delle cose dalle formule: essendoci i coefficienti a ed b, allora è possibile ricavare gli asintoti o conoscendo l’equazione o conoscendo i fuochi ed i vertici. Alla fine della pagina vedremo degli esempi su questi calcoli. Passiamo adesso all’ultimo aspetto di un iperbole: l’eccentricità.

Eccentricità dell’iperbole

Essenzialmente eccentricità di un iperbole significa “quanto è curva un iperbole”. Per calcolarla si utilizza la seguente formula.

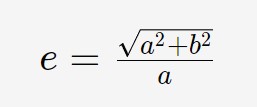
Quindi, a seconda del valore dei coefficienti a ed b, si hanno anche diversi valori di eccentricità. Quindi a seconda dell’equazione che ci viene data, un iperbole può avere diversi valori di eccentricità.

Essa è una misura di quanto marcata è la curva dell’iperbole, eccovi alcuni esempi.

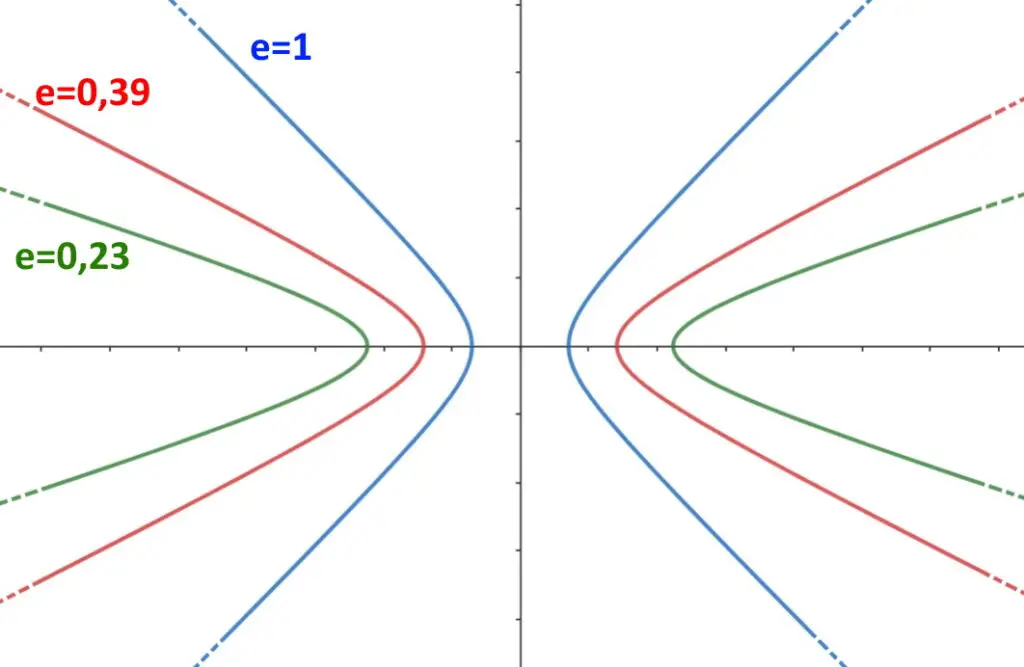
Adesso conosciamo tutto di un iperbole…con fuochi sull’asse x! Ora mostriamo anche gli altri tipi di iperboli, molto simili: quindi andremo più veloci e mostreremo solamente le formule.

Iperbole con fuochi sull’asse y

Il discorso è analogo al precedente. Quello che cambia è la disposizione spaziale dell’iperbole. Qui si ha un iperbole disposta in verticale, con la presenza di fuochi e di vertici sopra l’asse y.

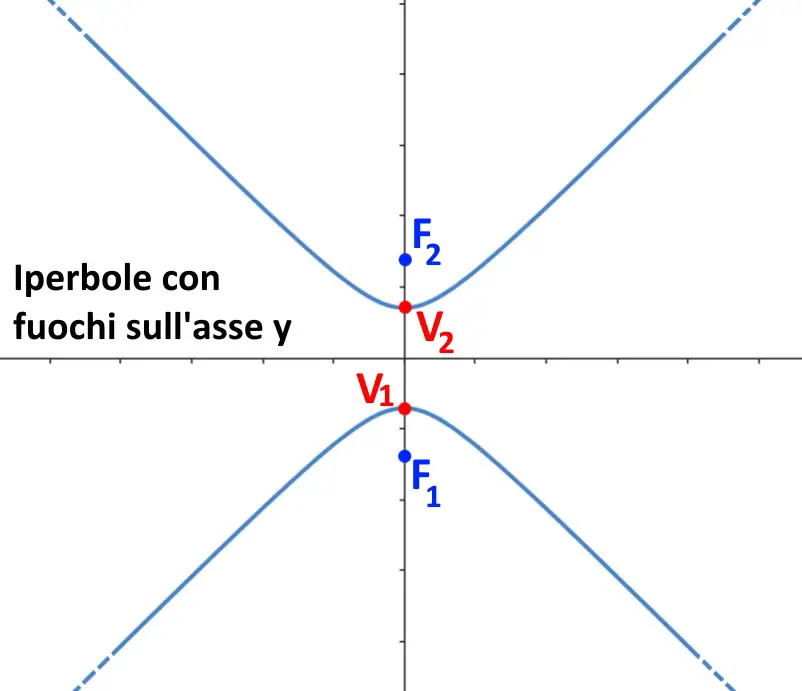
L’equazione è leggermente diversa, cambia infatti solamente il segno del membro di destra.

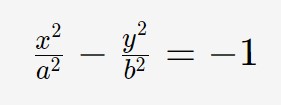
Tutte le considerazioni concettuali fatte prima valgono ancora. Quelle che cambiano sono le formule. Di fatti, essendo che i fuochi ed i vertici ora sono su un altro asse, ci aspettiamo chiaramente che le formule siano diverse, ed infatti è così.

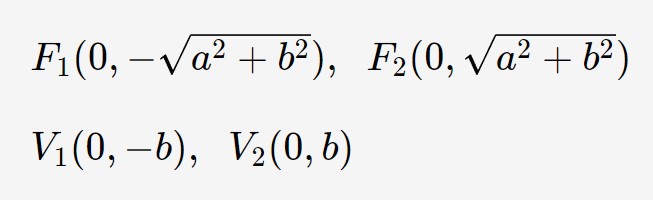
Osserviamo bene: notiamo che, a differenza delle formule di prima, alla fine sono state scambiate solo le componenti per i fuochi, mentre per i vertici abbiamo solo invertito le componenti e messo b. E’ questo un trucchetto per impararle: imparate dunque a memoria solo le formule di prima, e poi per ricavare queste invertite solo le componenti, e poi per i vertici metteteci la b.

Per gli asintoti le formule sono uguali! E’ questa un particolarità se ci pensate: asintoti uguali e cioè direzioni agli estremi uguali. Ciò che cambia è da dove parte l’iperbole in pratica.

Per l’eccentricità la formula è la stessa, ma cambia solo il denominatore:

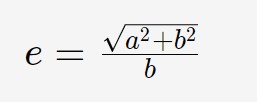
Vediamo ora un caso particolare, ma semplice, dell’iperbole: l’iperbole equilatera.

Iperbole equilatera

Anche qui vi abbiamo trattato una pagina a sé, cui invito a cliccarci: iperbole equilatera.

Un iperbole equilatera è semplicemente un iperbole che ha i coefficienti uguali. Quindi si chiama equilatera se ha:

a^2 = b^2 \implies a=b

Questa è l’unica condizione: di conseguenza un iperbole equilatera può avere sia i fuochi sull’asse x che sull’asse y. Cioè non importa che tipo sia, basta che valga tale condizione:

a=b \; \implies iperbole equilatera

Quindi, a seconda del fatto che sia con i fuochi sull’asse x o y segue diverse formule. Formule che vengono semplificate dal fatto che i coefficienti sono uguali. Formule e passaggi che trovate nella pagina dedicata sull’iperbole equilatera.

Esempi svolti e spiegati sull’iperbole

Esempio 1. Determinare l’equazione di un iperbole sapendo che F_1 (-5,0) e F_2 (5,0) , e conoscendo i vertici V_1 (-4,0) e V_2 (4,0) . Che tipo di iperbole è?

Osserviamo le coordinate dei fuochi e dei vertici, e disegniamoli in un grafico: stanno sull’asse x! Di conseguenza capiamo che l’iperbole ha i fuochi sull’asse x. La sua equazione dovrà essere dunque della forma:

\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1

Dobbiamo quindi trovare i coefficienti. Mettiamoci vicino le formule di questo tipo di iperbole. Notiamo fin da subito che i vertici hanno la forma:

V_1 (-a,0), \;\; V_2 (a,0)

Noi abbiamo:

V_1 (-4,0), \;\; V_2 (4,0)

Per confronto capiamo immediatamente che:

a=4 \implies a^2 = 16

A questo punto ci manca solamente b! Questo coefficiente lo troviamo nell‘informazione dei fuochi:

F_1 (-\sqrt{a^2 + b^2} ,0), \;\; F_2 (\sqrt{a^2 + b^2},0)

E noi abbiamo:

F_1 (-5 ,0), \;\; F_2 (5,0)

Per confronto di nuovo capiamo che:

\sqrt{a^2 + b^2} = 5

Ma noi conosciamo a:

\sqrt{16 + b^2} = 5

Eleviamo tutto al quadrato:

4 + b^2 = 25

b^2 = 25-16 = 9

Ora basta sostituire i coefficienti quadri nell’equazione dell’iperbole, ottenendo:

\frac{x^2}{16} - \frac{y^2}{9} = 1

Esempio 2. Determinare i fuochi, i vertici e gli asintoti dell’iperbole di equazione seguente:

4x^2 - y^2 = -16

Innanzitutto non spaventiamoci: sembra non avere la forma di un iperbole, ma in realtà lo è. Basta semplicemente dividere tutto per 16:

\frac{x^2}{4} - \frac{y^2}{16} = -1

Quindi abbiamo ottenuto l’equazione di un iperbole con fuochi sull’asse y. Capiamo immediatamente per confronto sempre, che:

a^2 = 4 \implies a= 2, \; b^2 = 16 \implies b= 4

Ora abbiamo tutto per trovare i fuochi ed i vertici. Partiamo dai fuochi, dobbiamo usare le seguenti formule (ricordate che dobbiamo usare le formule di un iperbole che ha i fuochi sull’asse y):

F_1 (0,-\sqrt{a^2 + b^2}), \;\; F_2 (0,\sqrt{a^2 + b^2})

Sostituendo i valori dei coefficienti:

F_1 (0,-\sqrt{4 + 16}), \;\; F_2 (0,\sqrt{4 + 16})

F_1 (0,-\sqrt{20}), \;\; F_2 (0,\sqrt{20})

Ora passiamo ai vertici:

V_1 (-b,0), \;\; V_2 (b,0)

V_1 (-4,0), \;\; V_2 (4,0)

Nulla di difficile: passiamo al calcolo degli asintoti, le cui formule sono:

y = \frac{b}{a} x, \; y = - \frac{b}{a} x

Facilmente ricaviamo che:

y = \frac{4}{2} x, \; y = - \frac{4}{2} x

y =2 x, \; y = - 2x

Esempio 3. Disegnare l’iperbole di equazione -1 - x^2 + \frac{y^2}{9} =0

Soluzione qui.

---

La pagina è conclusa, speriamo vi sia stato chiaro tutto.

Trovate altri centinaia di argomenti ed esercizi svolti di Matematica, di Geometria Analitica e Geometria.

Continuate a supportare il sito!