Fuoco parabola: formule, come calcolarlo ed esempi svolti
In questa pagina vedremo come calcolare il fuoco di una parabola, le formule da utilizzare nei diversi casi, ed alla fine della pagina vedremo degli esempi di esercizi svolti.
Indice
Che cos’è il fuoco di una parabola? E’ semplicemente un punto che serve, insieme alla direttrice, per definire la figura geometrica della parabola come luogo di punti. Non approfondiremo la definizione perché non serve negli esercizi! Vi basta sapere che il fuoco di una parabola sta sempre sull’asse della parabola, e sta posizionato un po’ più dentro rispetto al vertice.
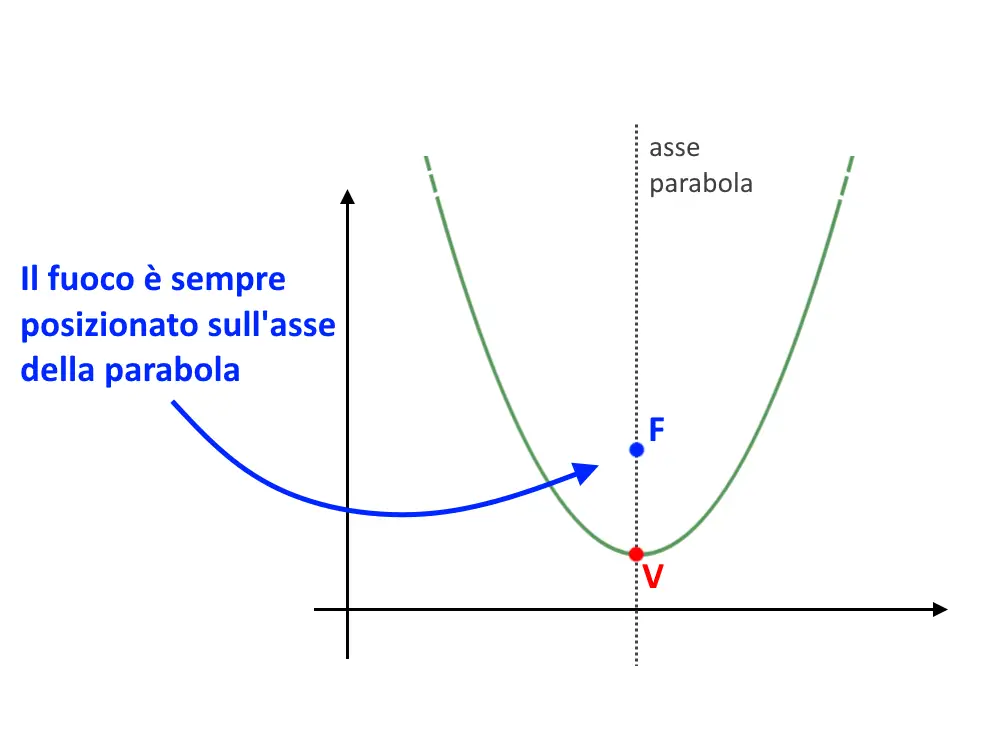
Ora che abbiamo capito cos’è, cominciamo con le formule! Iniziamo.
Formule del fuoco di una parabola
Come sappiamo, esistono diversi tipi di parabole, ognuna con formule leggermente diverse per calcolare il fuoco. Quindi le vedremo una per una velocemente, ma facendovi capire tutto, e vedremo caso per caso quali formule usare e trovare il punto del fuoco dov’è posizionato.
Fuoco in una parabola con vertice in origine ed asse coincidente ad asse y
Questo è il caso di una parabola che ha il vertice nell’origine degli assi cartesiani, quindi sempre nel punto (0,0), e poi ha l’asse che coincide con y. In questa tipologia di parabola, il fuoco è posizionato anch’esso sull’asse y sempre. Quindi abbiamo un qualcosa di questo tipo.
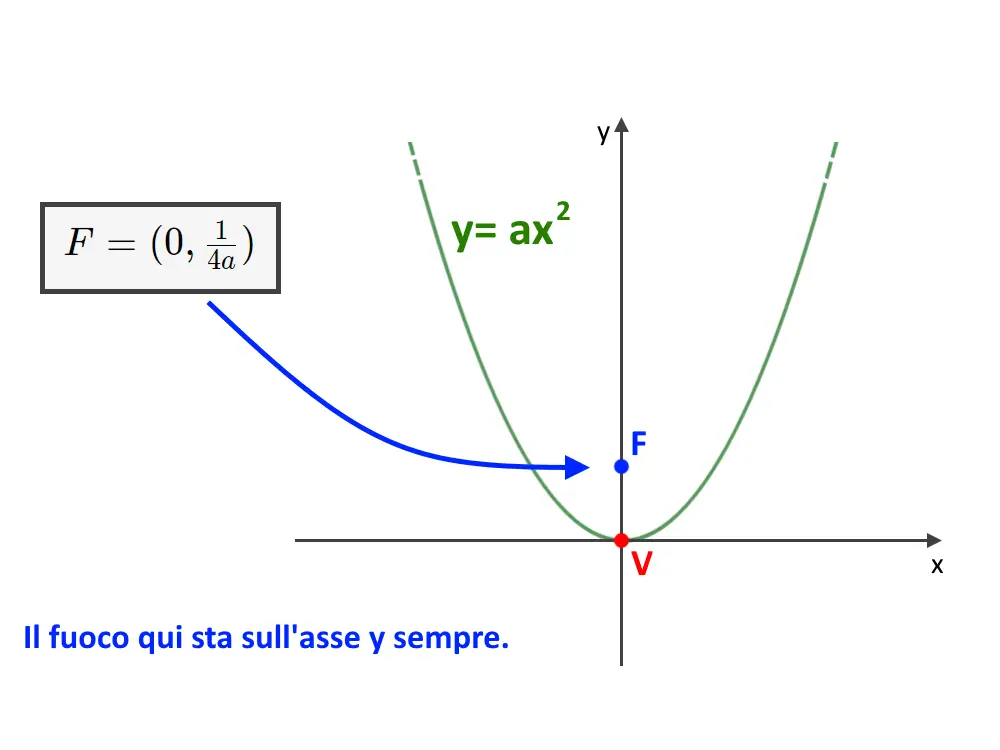
L’equazione di tale parabola è:
E la formula per calcolare il fuoco di questa parabola è la seguente.
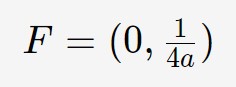
Come possiamo notare, l’unico parametro che fa variare il valore dell’ordinata del fuoco è il coefficiente a (perché 4 è costante, quindi a è l’unico che può cambiare in un problema). Di conseguenza, a seconda che tale coefficiente sia positivo o negativo, il fuoco si può trovare sotto o sopra. Vi mostriamo la differenza in questo schema.
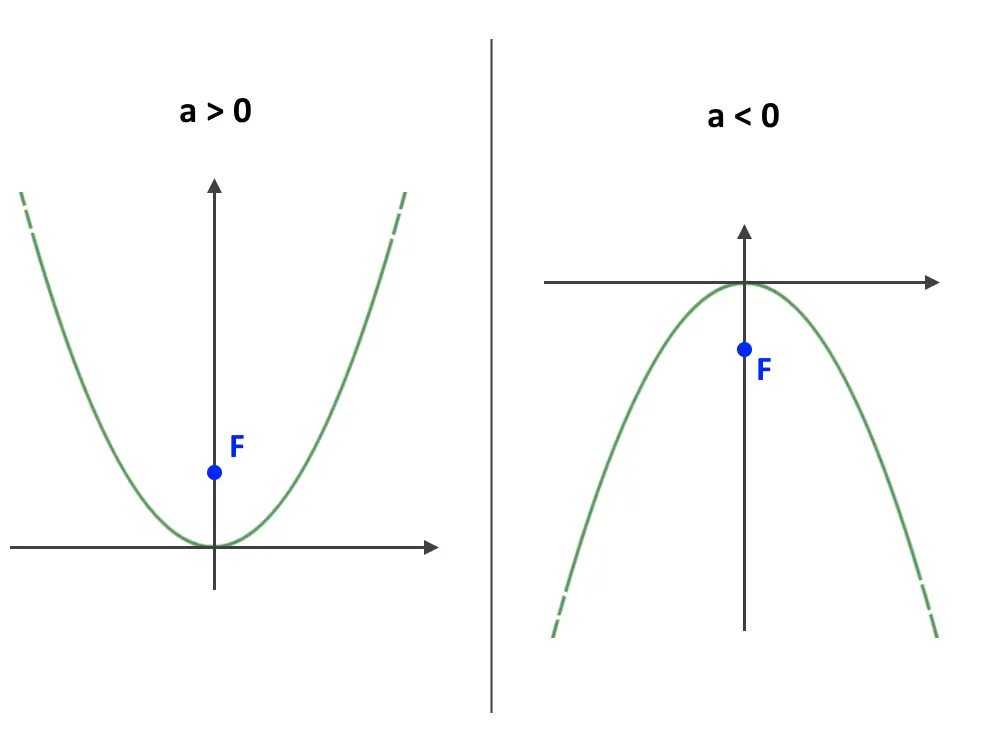
Per questo tipo di parabola abbiamo detto tutto ciò che ci serve.
Curiosità: il fuoco di una parabola è disposto in maniera opposta alla direttrice, rispetto al vertice. Più precisamente il punto di intersezione della direttrice con l’asse y ed il fuoco hanno la stessa distanza dal vertice.
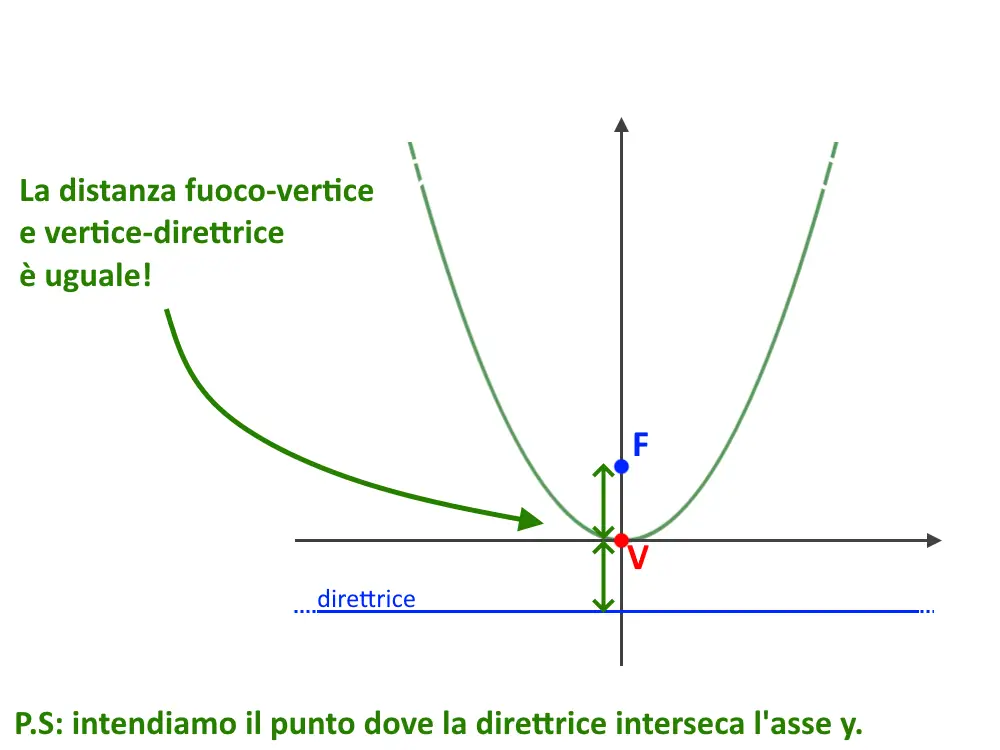
Questo è quindi anche un modo per vedere se alla fine ci troviamo!
Fuoco in una parabola con asse parallelo ad asse y
Qui abbiamo una parabola con vertice variabile nello spazio, in cui l’unica cosa certa è che l’asse è verticale, ossia parallelo all’asse y. In questo tipo di parabola il fuoco si trova sull’asse della parabola.
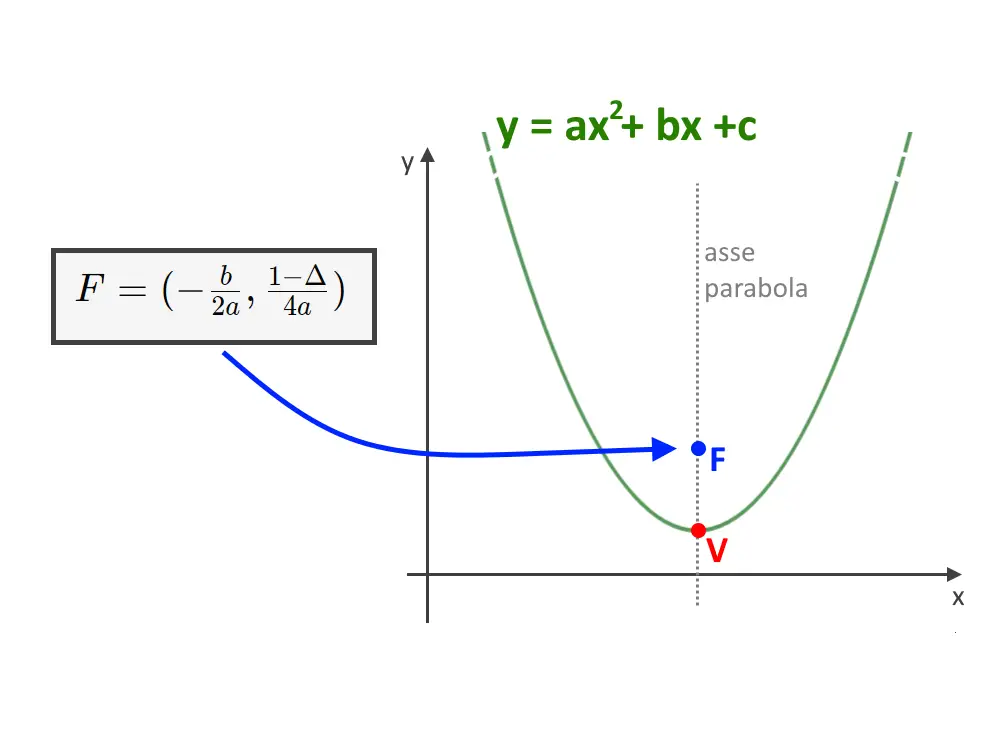
L’equazione di questa parabola è:
E qui la formula da usare per trovare il fuoco della parabola è la seguente.
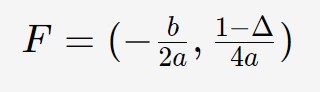
Quindi diversa rispetto a prima! Nonostante la presenza dei coefficienti l’unica cosa che fa sì che la parabola vada verso sopra o verso sotto è il coefficiente a (questo perché il termine quadratico domina). Allora a seconda del segno del coefficiente a, la parabola può essere disposta verso giù o verso su. Quindi anche il fuoco potrà essere posizionato giù o su rispetto al vertice.
Come nella curiosità di prima, un modo per vedere se alla fine ci troviamo è che il fuoco e la direttrice hanno stessa distanza dal vertice.
Passiamo all’ultimo caso di parabola!
Formula fuoco in una parabola con asse parallelo ad asse x
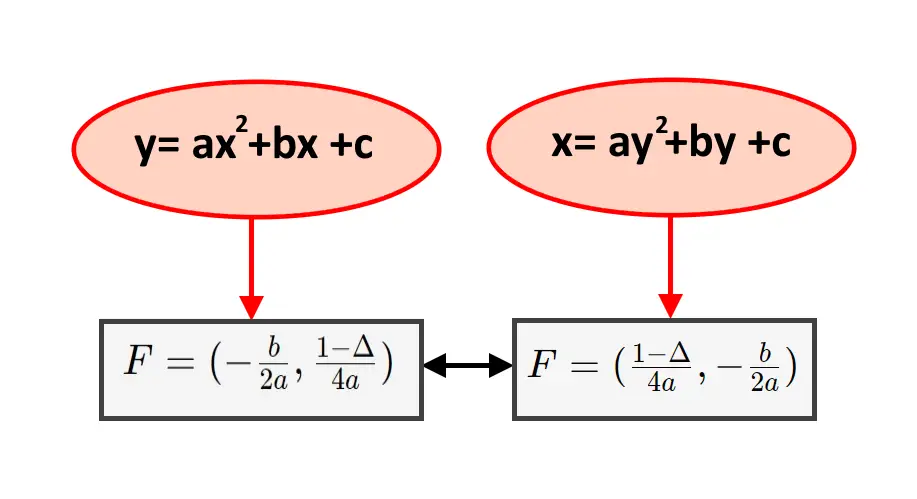
Questo è praticamente l’analogo del caso precedente. L’unica cosa che cambia è che l’asse della parabola è disposto in orizzontale, perciò parallelo all’asse x. Ancora, il fuoco sta sempre sull’asse della parabola, ma questa volta chiaramente sta sulla destra o sulla sinistra del vertice.
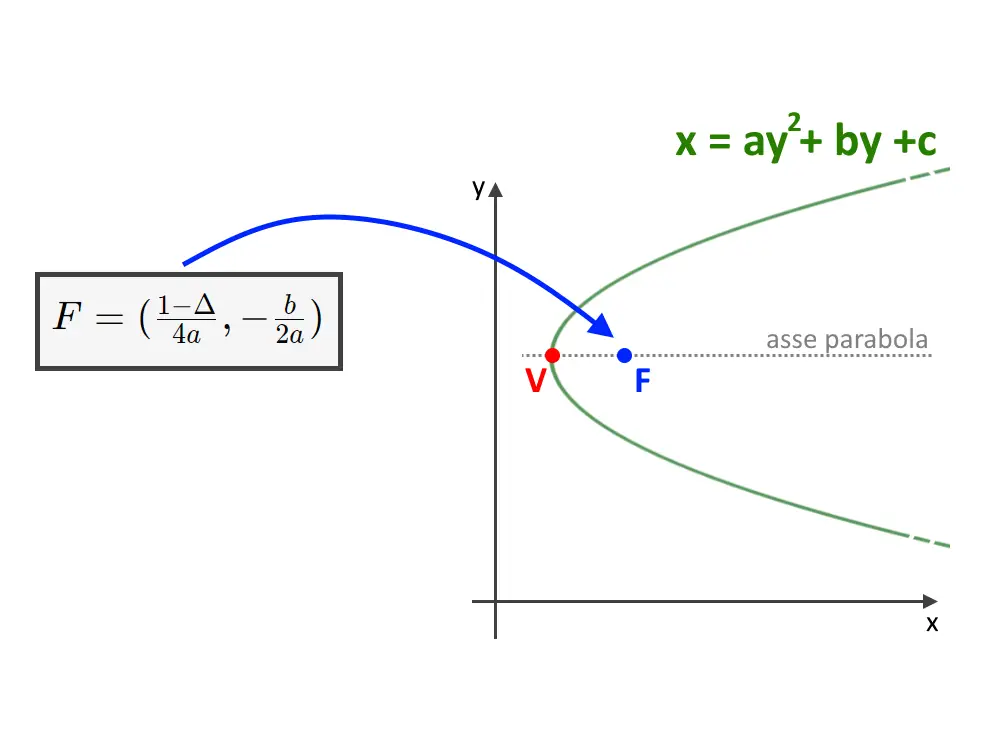
Qui vi insegniamo un trucchetto per ricordare questa formula! Allora: l’unica cosa che è cambiata è l’asse della parabola che prima era parallelo ad y, ora ad x. Questo si riflette anche nell’equazione della parabola stessa:
Dove abbiamo semplicemente scambiato x con la y. E questo si riflette nella formula del fuoco!
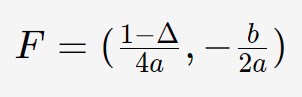
Osservate: le componenti del fuoco sono le stesse di prima ma invertite! Questo è un modo per evitare di memorizzare cose inutili.
Ottimo! Abbiamo finito con le diverse tipologie di parabola. Adesso passiamo a mettere in pratica tutto questo in alcuni esercizi svolti ed esempi.
Come calcolare il fuoco di una parabola: ESEMPI
Riassumiamo i passaggi mentali che seguiremo per ogni esercizio, applicabile con tutte le altre formule anche.
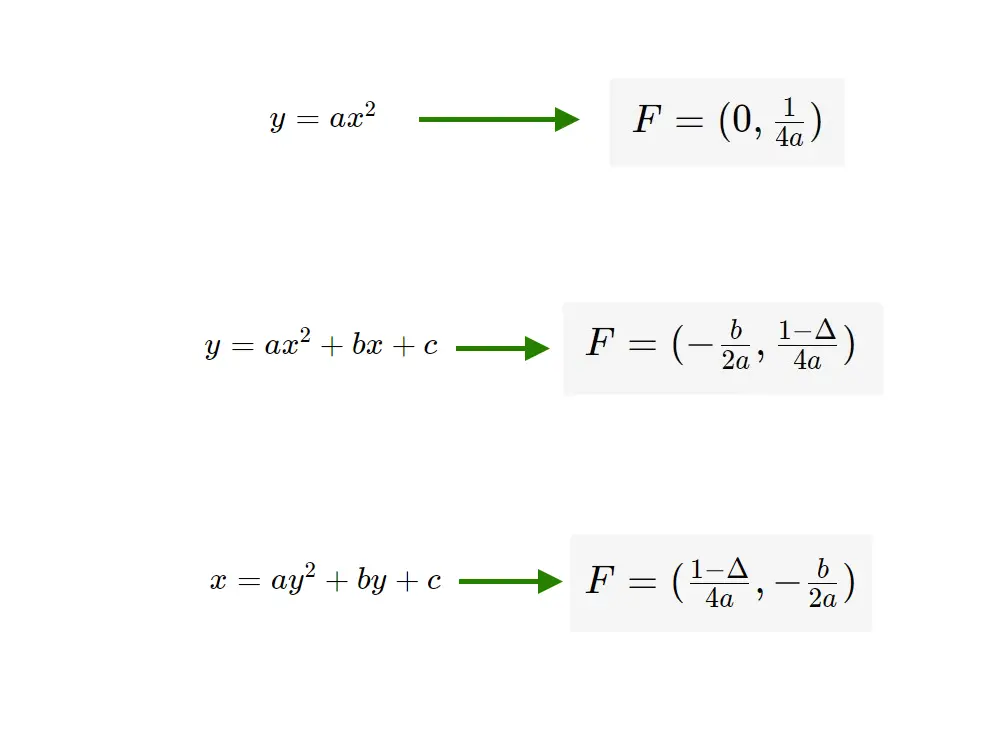
Esempio 1. Calcolare il fuoco della parabola avente equazione .
Prima cosa: di che parabola si tratta? Notiamo che la forma è quella di:
Di conseguenza che formula dobbiamo usare? Quella di questo tipo di parabola, cioè:
Dobbiamo capire chi è il coefficiente a. Lo capiamo dal confronto fra la nostra equazione dell’esercizio, e quella generale.
Ciò implica che . Ed allora sostituiamo questo valore nella formula!
Ed ecco svolto l’esercizio!
Esempio 2. Che fuoco ha la parabola seguente ?
Beh ci troviamo nel caso di una parabola della forma:
Ed allora dobbiamo utilizzare:
Col confronto capiamo che:
Ed inoltre ciò che ci serve è il delta! Il delta è lo stesso di quello di una equazione di secondo grado, quindi:
Non dobbiamo fare altro che sostituire tutti i valori nella formula delle coordinate del fuoco!
Nulla di così complicato: l’unica cosa da stare attenti è il segno! A volte un segno meno dentro la frazione può trarre in inganno con un altro segno meno che sta davanti alla frazione!
La pagina è conclusa, non servono altri esempi perché non è così complicato come vedete. Speriamo vi sia stato tutto chiaro.
Trovate tanti altri argomenti di Matematica, Geometria Analitica e anche Geometria.
Continuate a supportare il nostro sito!
parabola
calcolo
parabola
calcolo