Come trovare un punto su una retta: ESEMPI
Come trovare un punto su una retta: esempi. sapendo l’equazione di una retta nel piano cartesiano, come si trova un punto appartenete ad una retta di cui conosciamo l’equazione? In questa pagina risponderemo a questa domanda, e vedremo come si fa!
Indice
Iniziamo a vedere il procedimento (non difficile, non vi preoccupate) per trovare un punto su una retta!
Come trovare un punto appartenente ad una retta
Supponiamo che in un piano cartesiano conosciamo l’equazione di una retta, ad esempio:
y=3x
Tale retta, si presenta nel piano cartesiano nel modo seguente.
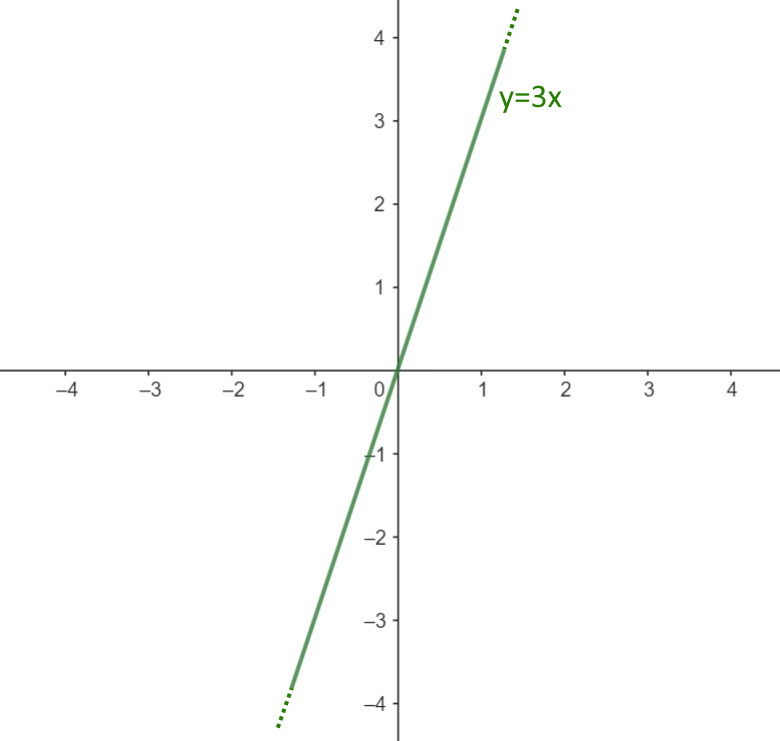
Per trovare un qualsiasi punto appartenente a questa retta, si parte dallo scegliere una componente x, poi sostituiamo tale valore x nell’equazione della retta, e ci ricaviamo la corrispondente componente y di tale punto. Vediamo subito un esempio per capire come! E’ più semplice di quel che si pensa.
Supponiamo che l’esercizio ci dica di volere trovare su questa retta il punto che ha come componente x=1. Quello che dobbiamo fare è sostituire x=1 nell’equazione della retta:
y=3x \implies y=3 \cdotp 1 = 3
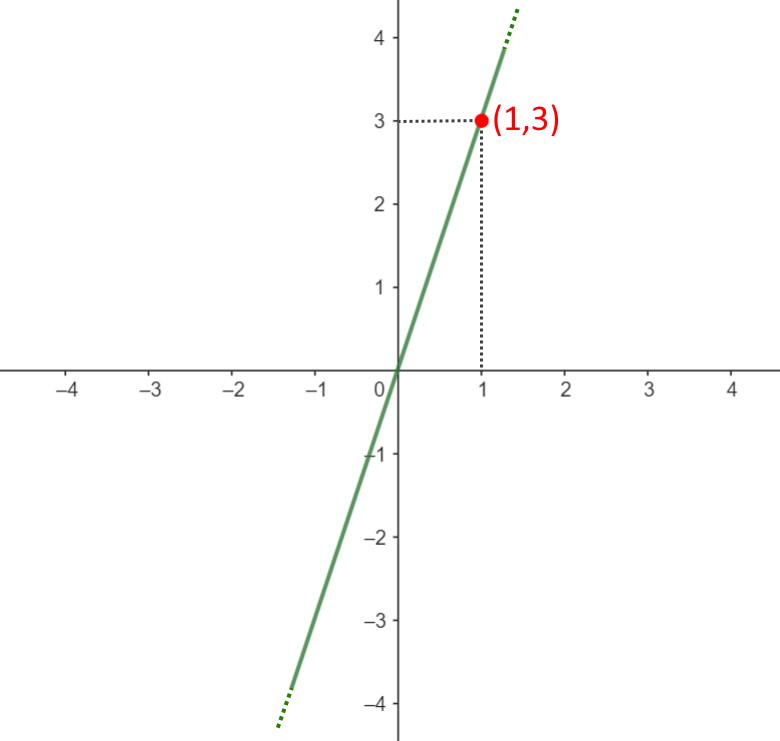
Abbiamo in questo modo trovato il punto sulla retta (1,3).
Come vedete dal grafico, per tracciare tale punto si parte dalla componente x=1 sull’asse delle ascisse e si traccia una linea verticale tratteggiata. Stessa cosa per la componente y=3: si traccia una linea tratteggiata orizzontale. Queste due linee tratteggiate si incroceranno in un punto, tale punto è proprio (1,3) che si troverà sulla retta!
Vediamo altri esempi su come determinare un punto su una retta.
Esempio 1. Consideriamo una retta di equazione y=x+3, determinare il punto su tale retta che ha come componente x=1.
In pratica l’esercizio ci sta dicendo che il punto sulla retta è del tipo (1,?). Il nostro obiettivo è trovare l’altra componente sull’asse y, sapendo l’equazione della retta. Come prima, per trovarlo basta sostituire la componente x=1 nell’equazione della retta:
y=x+3 \implies y=1+3 = 4
Questa è l’altra componente (LEGATA a x=1) del punto sulla retta (1,4).
Esempio 2. Determinare il punto su una retta di equazione y=-x+2 che ha come componente y=0.
Qui invece abbiamo il caso inverso: questa volta l’esercizio ci dice la componente y del punto sulla retta.
Di conseguenza ora per trovare tale punto di componente y=0 sulla retta, dobbiamo sostituire y=0 all’equazione della retta:
y=-x+2 \implies 0=-x+2
A questo punto portiamo la x a primo membro:
\implies x=2
Abbiamo così ricavato la componente x=2 relativa a y=0 del punto sulla retta!
Il punto sulla retta è quindi (2,0).
Vediamo adesso come trovare più punti su una retta, nulla di difficile!
Come trovare più punti su una retta
Esempio 3. Sia la retta di equazione y=-2x, trovare due qualsiasi punti su tale retta a piacere.
Il procedimento è simile, semplicemente dobbiamo farlo due volte. Qui l’esercizio ci chiede di trovare due punti a piacere appartenenti alla retta. Quindi partiamo dallo scegliere una qualsiasi componente x…ad esempio x=2. Sostituiamo nell’equazione della retta per ricavarci la corrispondente componente y di tale punto sulla retta:
y=-2x \implies y=-2 \cdotp 2 = -4
Quindi il primo punto su tale retta è (2,-4).
Adesso come secondo punto vediamo un caso che potrebbe far sbagliare: scegliamo ad esempio la componente x=-3 di un altro punto. Sostituiamo:
y=-2x \implies y=-2 \cdotp -3 = 6
Attenti che qui avete un meno per meno che fa +!
Questo secondo punto sulla retta è quindi (-3,6).
Quando si hanno due punti si può anche disegnare il grafico della retta! Visto che per due punti passa una ed una sola retta, basta disegnare i due punti trovati nel piano cartesiano e tracciare la retta passante per questi due punti.
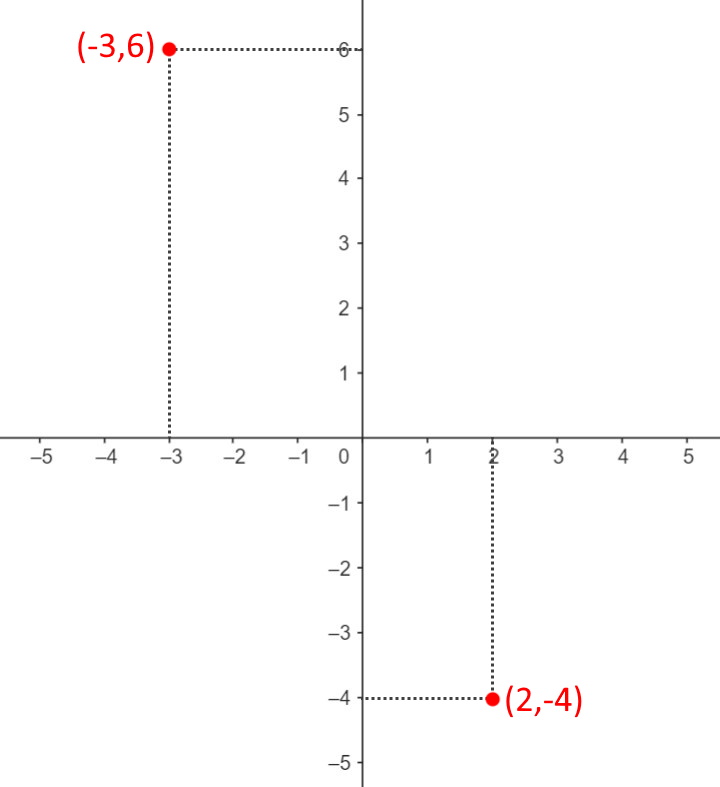
E quindi la retta passante per questi due punti, che ha come equazione y=-2x è la seguente.
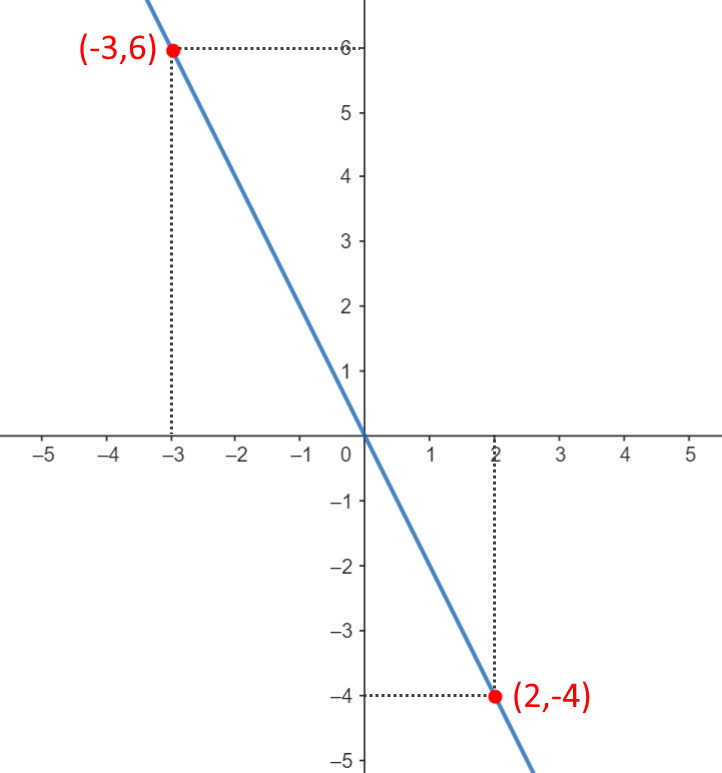
Esempio 4. Trovare i tre punti con componenti x=1,2 e y=3 che appartengono alla retta di equazione x+y-1=0.
Qui l’esercizio ci dà l’equazione di una retta scritta in forma implicita (cioè con tutto a primo membro). Per ricavare la forma esplicita (cioè quella classica con la y a sinistra) portiamo tutto a secondo membro tranne la y chiaramente:
\implies y= -x+1
A questo punto che abbiamo l’equazione della retta scritta in maniera comoda per noi, troviamo i tre punti!
Partiamo dal primo punto che ha come componente x=1:
y= -x+1 \implies y=-1+1=0
Il primo punto su tale retta è quindi la coppia (1,0). Passiamo al secondo punto, per il quale l’esercizio ci dice avere componente x=2:
y= -x+1 \implies y=-2+1=-1
Il primo punto su tale retta è quindi la coppia (2,-1). Per il terzo punto c’è da fare il procedimento inverso, nel senso che l’esercizio ci dà adesso la componente y=3! Quindi, come fatto prima, prendiamo l’equazione della retta ed isoliamo a sinistra la x, come segue:
y= -x+1 \implies x= 1-y
Adesso sì che possiamo sostituire la componente y!
y= -x+1 \implies x= 1-3 = -2
Il terzo punto sulla retta è quindi (-2,3)!
Attenti all’ordine mi raccomando, viene sempre prima la x e poi la y in (x,y) riguardo un punto!
In questa pagina abbiamo visto come trovare e determinare un punto su una retta. Come vedete non è così complicato.
Trovate altre centinaia di esercizi svolti e argomenti sia di matematica, che di geometria analitica e geometria! Continuate a studiare sul nostro nuovo sito!
Per approfondire:
https://it.wikipedia.org/wiki/Retta_nel_piano_cartesiano
punto su
una retta