Come trovare l’equazione della retta: ESEMPI
Come trovare l’equazione della retta: ESEMPI. In questa pagina vedremo tutti i casi sul come trovare l’equazione di una retta. L’indice seguente sintetizza i punti principali che tratteremo, e quelli che vi possono capitare nella verifica in classe. Spiegheremo tutto con calma, e gli esercizi svolti saranno risolti passo dopo passo. Iniziamo subito e non perdiamoci in chiacchiere.
Indice
- Come trovare l’equazione della retta passante per un punto
- Come determinare l’equazione di una retta passante per due punti
Partiamo col primo caso, ossia abbiamo che in un piano cartesiano sappiamo che la retta passa per un punto specifico.
Come trovare l’equazione della retta passante per un punto
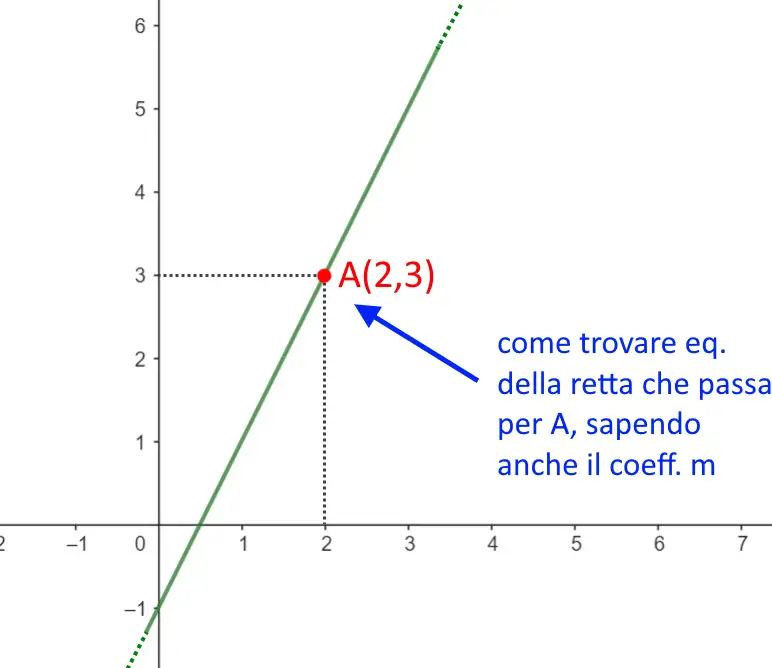
Introduciamo il problema: dobbiamo calcolare l’equazione di una retta in un piano cartesiano, che è sempre della forma:
y=mx + q
L’unico dato che l’esercizio ci dirà è che abbiamo che la retta passa per un punto specifico, ad esempio per A=(0,3). Inoltre il problema ci dirà anche il coefficiente angolare, ossia il coefficiente m. Supponiamo che sia m=2.
Adesso come si trova la retta passante per A=(0,3)? Per determinare l’equazione di tale retta utilizziamo la seguente formula: formula di una retta passante per un punto.
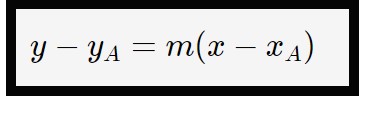
Per capirla e non confonderci, vediamo cosa significano i vari termini di questa formula: y ed x bisogna lasciarli sempre così come sono, senza toccarli. Il coefficiente m sarebbe il coefficiente angolare, e quindi dobbiamo sostituire il suo valore se l’abbiamo. I due termini y_A e x_A sono le componenti del punto A in cui la retta passa, quindi dobbiamo sostituire a questi le rispettive componenti del punto che ci dà l’esercizio.
Nell’esempio fatto, quindi dovremmo sostituire in questa formula i valori m=2, e poi y_A = 3 e poi anche x_A = 0. Otteniamo:
y - 3 = 2 (x-0)
y - 3 = 2x
Per ottenere la classica equazione esplicita di una retta, isoliamo a sinistra la y, quindi portiamo tutto a secondo membro come segue.
y = 2x +3
Ed abbiamo così ottenuto l’equazione della retta che ci serviva e volevamo trovare! Quindi RICORDATE: se avete come dato retta passante per un solo punto usate la formula di sopra!
Vediamo alcuni esercizi svolti adesso, e diversi casi che possono capitare nella verifica in classe.
Esercizio 1. Determinare l’equazione della retta con coefficiente angolare m=-1 e che passa per il punto A=(-1,2).
Nella traccia dell’esercizio leggiamo immediatamente “retta che passa per il punto“, quindi utilizziamo la formula sopra detta!
y - y_A = m (x-x_A)
Sostituiamo i dati che abbiamo (attenti ai segni, quando ci sono dei punti col meno mettete le parentesi):
y - 2 = -1 (x-(-1))
y - 2 = -1 (x+1)
Svolgiamo la moltiplicazione con la parentesi, ricordate che un segno meno davanti alla parentesi cambia tutto di segno.
y - 2 = -x-1
E per ottenere la forma esplicita di una retta, isoliamo a sinistra la y da sola:
y = -x-1+2
y = -x +1
Abbiamo così ottenuto l’equazione della retta passante per A!
Esercizio 2. Scrivi l’equazione di una retta passante per il punto A=(-1,2) e che è parallela all’asse x.
Come vedete manca un dato, cioè la conoscenza del coefficiente m! Come lo troviamo? Tale dato ce lo dà l’informazione del fatto che la retta è parallela all’asse x. Dovete infatti sapere che:
Retta parallela ad asse x= coefficiente angolare m=0.
Scrivetevi questa cosa da qualche parte che può tornarvi utile! Ora che abbiamo trovato m, riprendiamo la formula della retta passante per un punto ed applichiamola.
y - y_A = m (x-x_A)
y - 2 = 0 \cdotp (x-(-1))
Uno zero che moltiplica un qualcosa dà ancora zero:
y - 2 = 0
Isoliamo la y a sinistra:
y = 2
E quindi questa è l’equazione della retta! Può sembrare strano che non compaia una x, ma è così se la retta è parallela all’asse x!
Vediamo ora il caso di una retta che passa invece per due punti!
Come determinare l’equazione di una retta passante per DUE punti
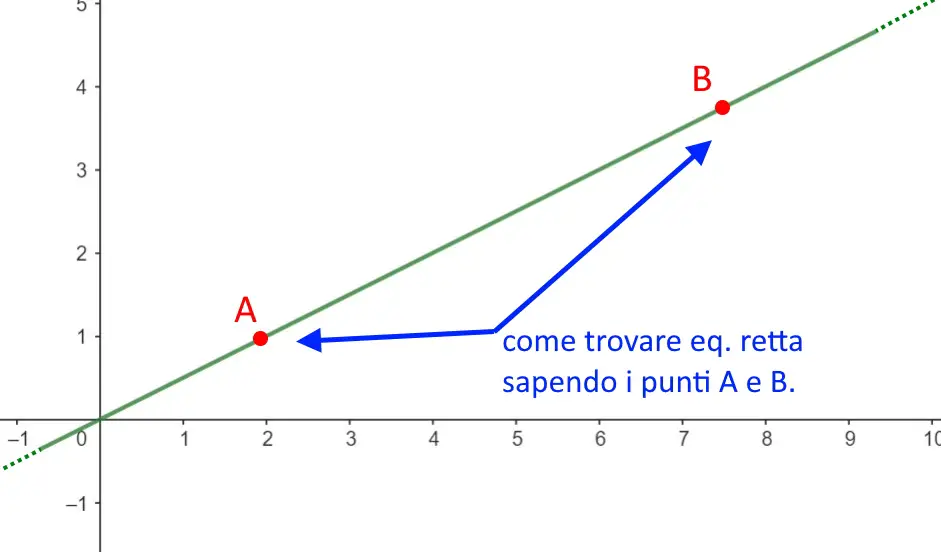
Ora vediamo il caso invece del determinare l’equazione di una retta che passa per DUE punti! Ora quindi sono due i punti, e non più uno. L’esercizio quindi vi dirà i due punti A e B, ma NON vi dirà il coefficiente angolare.
Di fatti, la conoscenza di m non serve in questo caso. La formula che andremo ad utilizzare quando sentiremo parlare di retta passante per due punti è la seguente.
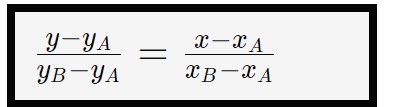
Spieghiamo cosa significa questa formula, per non confonderci: questa formula ci permette di ricavare l’equazione della retta che passa per A e B, sfruttando il fatto che per due punti passa una ed una sola retta.
I due termini y e x che compaiono nella formula non vanno toccati o sostituiti. Ai valori y_A, \; x_A sostituiremo le componenti del punto A, e faremo lo stesso con y_B, \; x_B per quanto riguarda il punto B.
Ricordate che x_B significa la componente x del punto B.
Vediamo subito un esempio per capire meglio, ed applicare tale formula.
Esercizio 1. Trovare l’equazione della retta che passa per i punti A=(3,0) e B=(0,5).
Questo, come leggete dalla traccia, è il caso della “retta che passa per due punti“, quindi utilizziamo la formula sopra indicata!
\frac{y- y_A}{y_B - y_A} = \frac{x- x_A}{x_B - x_A}
Sostituiamo le componenti dei due punti: su questo passaggio capita molto spesso di sbagliare e confondersi con le componenti, quindi ricontrollate sempre questo passaggio di sostituzione, fidatevi!
\frac{y- 0}{5 - 0} = \frac{x- 3}{0 - 3}
\frac{y}{5 } = \frac{x- 3}{- 3}
Ora quello che vogliamo andare a fare per ricavare l’equazione esplicita di una retta, è avere la y isolata a sinistra senza nient’altro. Quindi moltiplichiamo tutto per 5:
5 \cdotp \frac{y}{5 } = 5 \cdotp \frac{x- 3}{- 3}
y = \frac{5(x- 3)}{- 3}
Quindi:
y = \frac{5x- 15 }{- 3}
La forma non è ancora quella giusta, perché vogliamo qualcosa del tipo:
y=mx + q
Allora andiamo a SPEZZARE la frazione, ossia per una proprietà delle frazioni possiamo scrivere:
y = \frac{5x}{- 3} - \frac{ 15 }{- 3}
y = - \frac{5}{3}x + \frac{ 15 }{3}
Ed otteniamo finalmente l’equazione della retta scritta in forma esplicita:
y = - \frac{5}{3}x + 5
Quindi qui come vedete c’è bisogno di qualche passaggio in più!
Esercizio 2. Determinare il coefficiente angolare della retta passante per i due punti A=(\frac{1}{3},-\frac{1}{2}) e B=(\frac{2}{3},-\frac{3}{2}).
Il primo passo sarà applicare la formula e trovare così l’equazione della retta, che sarà un qualcosa del tipo:
y=mx + q
A quel punto basterà vedere che numero è m, ed il gioco è fatto.
Quindi partiamo con l’utilizzare la formula della retta passante per due punti:
\frac{y- y_A}{y_B - y_A} = \frac{x- x_A}{x_B - x_A}
Sostituiamo i valori che abbiamo, stando attenti ai segni meno.
\frac{y- (-\frac{1}{2}) }{-\frac{3}{2} - (-\frac{1}{2} ) } = \frac{x- \frac{1}{3} }{\frac{2}{3} - \frac{1}{3} }
\frac{y+\frac{1}{2} }{-\frac{3}{2} +\frac{1}{2} } = \frac{x- \frac{1}{3} }{\frac{2}{3} - \frac{1}{3} }
Ora effettuiamo solo ai denominatori il minimo comune multiplo:
\frac{y+\frac{1}{2} }{\frac{-3+1}{2} } = \frac{x- \frac{1}{3} }{\frac{2-1}{3} }
\frac{y+\frac{1}{2} }{-1 } = \frac{x- \frac{1}{3} }{\frac{1}{3} }
A secondo membro compare una frazione di frazione, di conseguenza per ridurlo ad una forma più semplice portiamo il suo denominatore sopra capovolgendolo (cioè lo giriamo, gli scambiamo denominatore col numeratore):
\frac{y+\frac{1}{2} }{-1 } = (x- \frac{1}{3}) \frac{3}{1}
\frac{y+\frac{1}{2} }{-1 } = 3(x- \frac{1}{3})
Ossia:
\frac{y+\frac{1}{2} }{-1 } = 3x- 1
A questo punto, dobbiamo levare la frazione al primo membro, visto che vogliamo la y da sola. Quindi moltiplichiamo tutto per -1, ottenendo:
y+\frac{1}{2} = -3x+1
y = -3x+1 -\frac{1}{2}
Sommiamo, facendo il minimo comune multiplo solamente i termini noti (la x la lasciamo stare perché sta bene):
y = -3x +\frac{2-1}{2}
y = -3x +\frac{1}{2}
Ecco l’equazione della retta trovata! L’esercizio ci chiede però “qual è il suo coefficiente angolare m”? Il coefficiente angolare, come vedete dalla generica forma:
y=mx + q
E’ semplicemente ciò che sta dietro la x, quindi:
m=-3
In questa pagina abbiamo visto i due casi che possono capitare se vi chiedono di calcolare l’equazione di una retta. Trovate comunque altre centinaia di esercizi sia di matematica che di geometria analitica e di geometria!
Continuate a studiare sul nostro sito!
Per approfondire:
https://it.wikipedia.org/wiki/Retta_nel_piano_cartesiano
punto su
una retta
rette sono
parallele