Come disegnare un iperbole: esempi svolti
Come disegnare un iperbole: esempi svolti. In questa pagina vedremo come si disegna un iperbole passo dopo passo, tra cui anche il grafico di una iperbole equilatera. Ci sono tre tipi di iperbole che vi possono capitare: con i fuochi sull’asse x, con i fuochi sull’asse y, iperbole equilatera: li vedremo uno per uno con calma. Sarete pronti per la verifica in classe!
Indice
- Come disegnare un iperbole con fuochi sull’asse x
- Come disegnare un iperbole con fuochi sull’asse y
- Come fare il grafico di un’iperbole equilatera
Abbiamo quindi detto che disegnare una iperbole racchiude tre casi diversi, ma con molti punti in comune. Iniziamo a vedere come si disegna un iperbole con i fuochi che stanno sull’asse x.
Come disegnare un iperbole con fuochi sull’asse x
Riassumiamo in maniera compatta ed efficiente tutte le formule che servono e che sono utili per il disegno di una iperbole con fuochi sull’asse x.
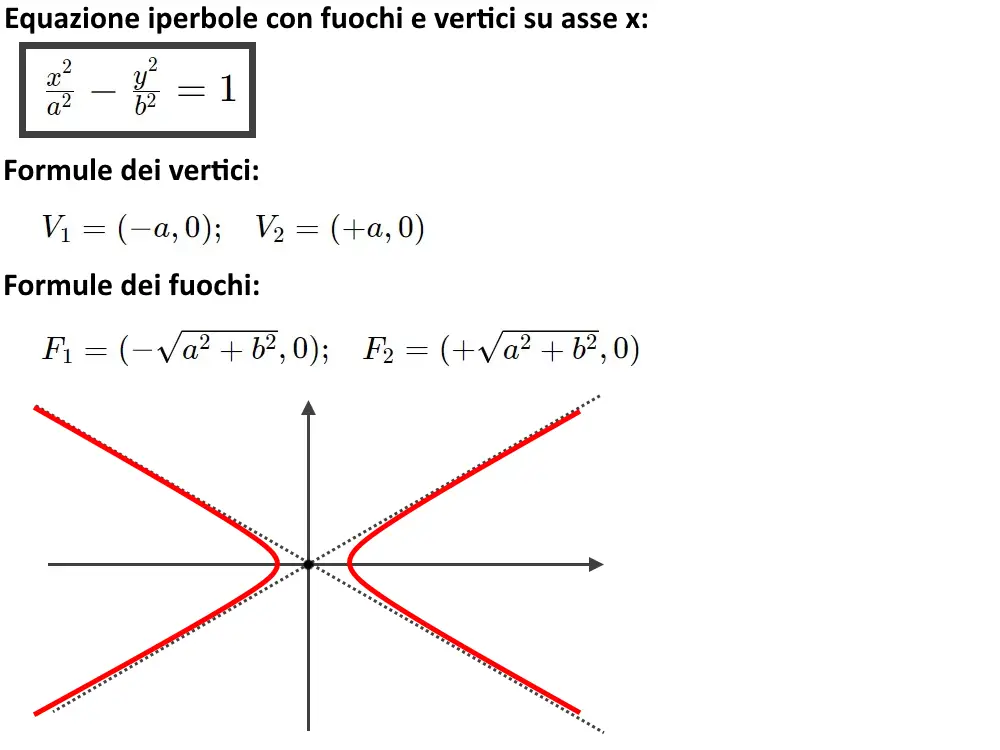
Il grafico di una iperbole possiamo riassumerla in questi punti principali:
- Ridurre l’equazione che vi dà l’esercizio, a quella di una classica iperbole
- Calcolare e disegnare i due vertici
- Calcolare e disegnare i due fuochi
- Disegnare gli asintoti
- Disegnare l’iperbole
Vediamo subito come si fa!
Esercizio 1. Disegnare il grafico della seguente iperbole \frac{x^2}{8} - \frac{2y^2}{9} = 2 .
Una iperbole con i fuochi (ed i vertici) che stanno sopra l’asse x, come vedete dalle formule sopra, ha la forma generale seguente:
\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1
A noi però a destra, a secondo membro, NON c’è un 1 ma c’è un 2! E poi non c’è neanche una y^2 da sola. Quindi per primissima cosa andiamo a dividere tutto per 2, per ottenere la forma comune di una iperbole ed usare senza problemi tutte le formule per farne il grafico!
\frac{1}{2} \frac{x^2}{8} - \frac{1}{2} \frac{2y^2}{9} = \frac{2}{2}
\frac{x^2}{16} - \frac{y^2}{9} = 1
Abbiamo così ottenuto una classica equazione dell’iperbole.
Per confronto con:
\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1
Otteniamo allora che:
a^2=16 \implies a= \pm \sqrt{16} = \pm 4
b^2=9 \implies b= \pm \sqrt{9} = \pm 3
Ora che abbiamo i coefficienti a e b, possiamo iniziare a calcolare e disegnare i vertici ed i fuochi seguendo le formule. Partiamo dai due vertici:
V_1 = (-a,0) \implies V_1 = (- 4 , 0)
(Con -a e -b nelle formule si intende di prendere la soluzione col segno meno)
V_2 = (+a,0) \implies V_2 = (+ 4, 0)
Disegniamoli nel piano cartesiano!
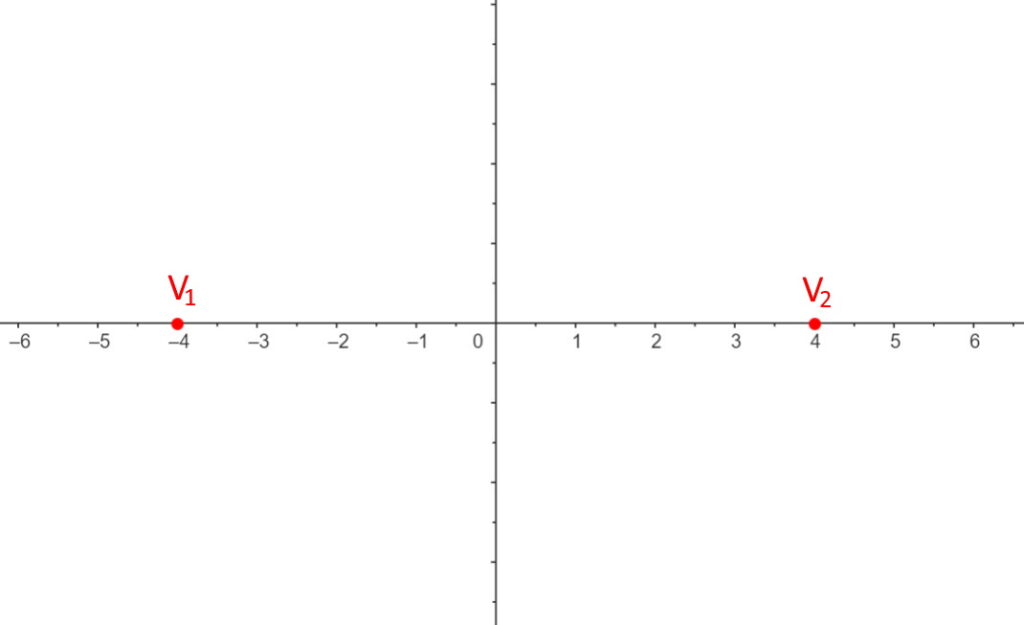
Adesso passiamo al calcolo dei due fuochi:
F_1 = (-\sqrt{a^2 +b^2},0) \implies F_1 = (- \sqrt{16+9} , 0) = (-5,0)
F_2 = (+\sqrt{a^2 +b^2},0) \implies F_2 = (+ \sqrt{16+9} , 0) = (+5,0)
Disegniamo anche questi due punti nel piano cartesiano!
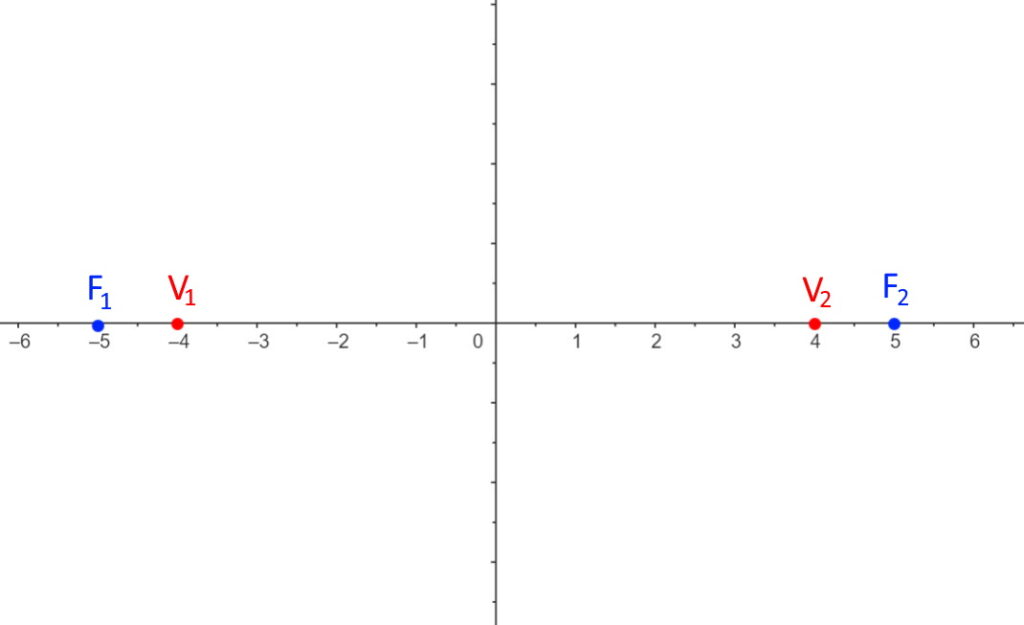
Adesso dobbiamo disegnare gli asintoti, che sono estremamente importanti per il disegno. Come si fa? E’ in realtà molto semplice: segniamo i seguenti 4 punti seguenti (vedete dalla figura dopo, formano una sorta di rettangolo):
\begin{cases} (a,b) \\ (-a,b) \\ (a,-b) \\ (-a,-b) \end{cases}
Che sarebbero nel nostro caso:
\begin{cases} (16,9) \\ (-16,9) \\ (16,-9) \\ (-16,-9) \end{cases}
E gli asintoti sono semplicemente le rette che passano per le coppie di vertici opposti fra di loro, come segue.
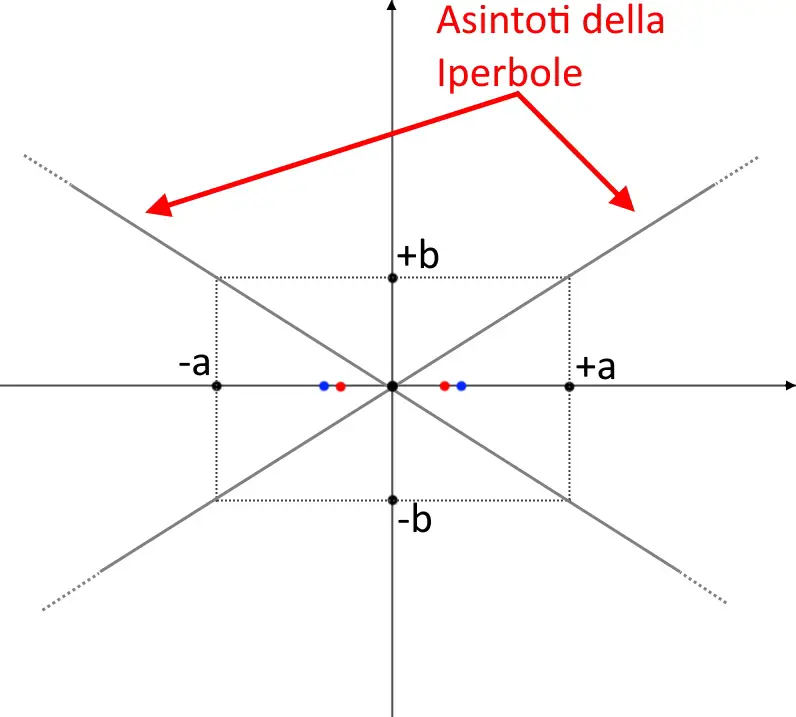
A questo punto abbiamo tutto ciò che ci serve per disegnare una iperbole. Facciamola partire dal vertice, e facciamola tendere agli asintoti, senza mai farli toccare! Il gioco è fatto!
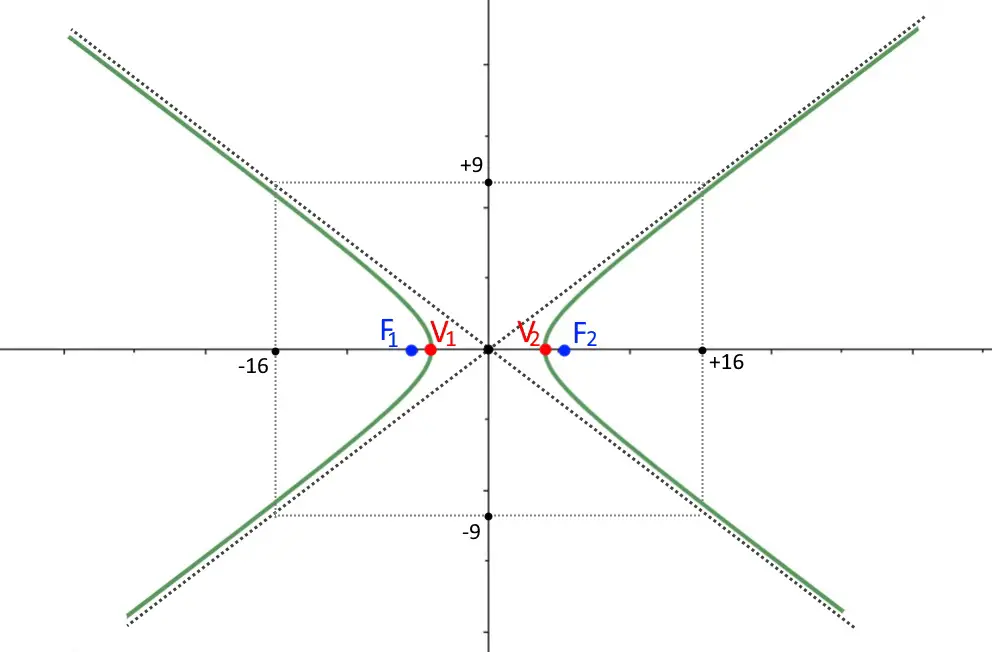
Se ve lo state chiedendo l’eccentricità non serve per il grafico di una iperbole.
In linea di massima non vi serve esercitarvi molto: il disegno di una iperbole con fuochi sull’asse x è sempre uguale bene o male.
Come disegnare un iperbole con fuochi sull’asse y
Anche qui riassumiamo le formule dell’iperbole, questa volta con fuochi sull’asse y. Non sono molto diverse da quelle di prima, anzi sono quasi tutte uguali ma con componente x e y invertita. Quindi non è così difficile memorizzarle per la verifica in classe!
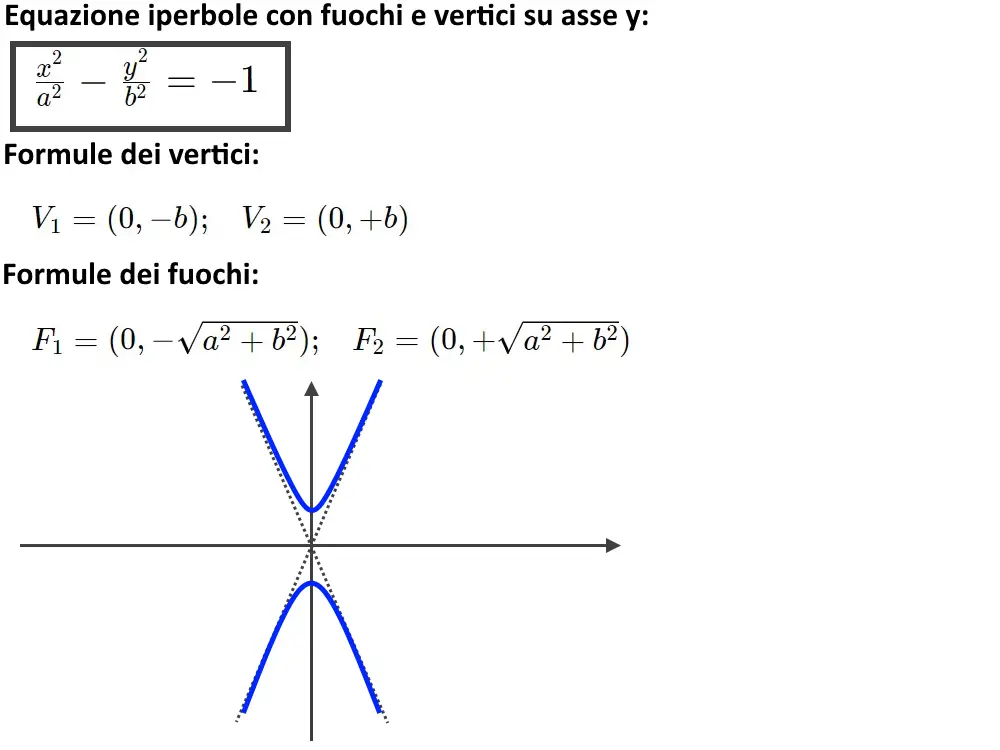
I punti principali che seguiremo sono gli stessi identici a quelli di prima!
Esercizio 2. Disegnare l’iperbole di equazione -1 -x^2 + \frac{y^2}{9} = 0 .
La domanda per questo esercizio sorge spontanea: che tipo di iperbole è? Non è sicuramente una classica equazione di una iperbole. Quindi iniziamo a portare il -1 a secondo membro:
-x^2 + 9y^2 = 1
Adesso cambiamo tutto di segno:
x^2 - \frac{y^2}{9} = -1
Come vedete, abbiamo ottenuto una prima informazione. Essa è una iperbole con fuochi e vertici sopra l’asse y, cioè della forma:
\frac{x^2}{a^2} - \frac{y^2}{b^2} = -1
E per confronto ricaviamo che i coefficienti sono:
a^2=1 \implies a= \pm 1
b^2=9 \implies b= \pm \sqrt{9} = \pm 3
Ora che sappiamo chi sono i coefficienti a e b, indispensabili nelle formule, possiamo calcolare la posizione dei due vertici:
V_1 = (0,-b) \implies V_1 = (0,-3)
V_2 = (0,+b) \implies V_2 = (0, +3)
Come vedete non cambia molto rispetto all’esercizio precedente, la differenza sta nel fatto che ora i punti principali sono sopra l’asse y.
Calcoliamo adesso i due fuochi, e andiamo a segnare questi punti nel piano cartesiano del nostro quaderno!
F_1 = (0,-\sqrt{a^2 +b^2}) \implies F_1 = (0,- \sqrt{1+9} ) = (0,-\sqrt{10})
F_2 = (0,+\sqrt{a^2 +b^2}) \implies F_2 = (0,+ \sqrt{1+9} ) = (0,+\sqrt{10})
Disegniamo queste prime informazioni!
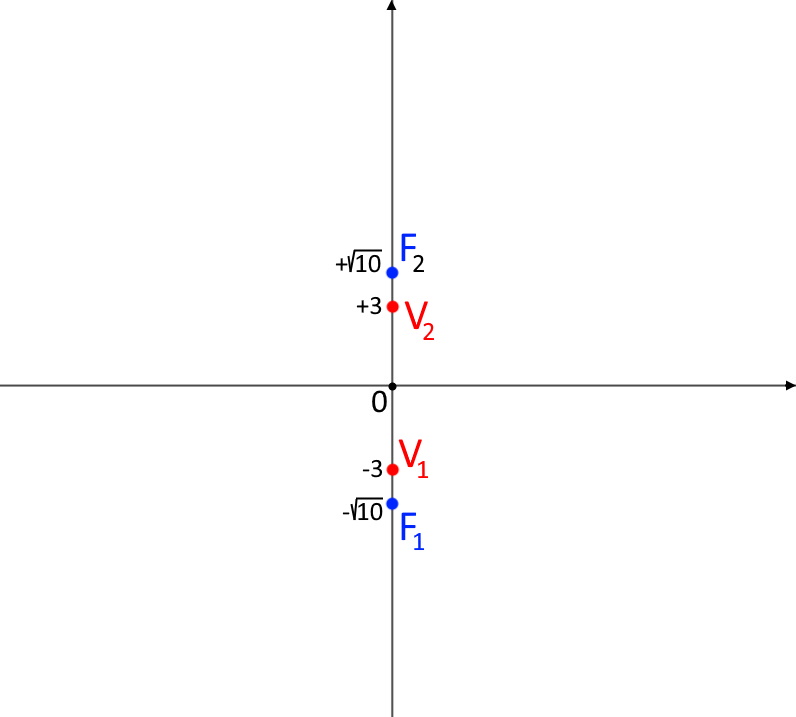
Ora è il momento di disegnare e trovare i due asintoti dell’iperbole. Seguiamo esattamente lo stesso procedimento di prima, ossia segniamo sul piano i seguenti punti (gli stessi dell’altro caso di iperbole), che formano un rettangolo.
\begin{cases} (a,b) \\ (-a,b) \\ (a,-b) \\ (-a,-b) \end{cases}
Che nel nostro caso, sostituendo i due coefficienti di questo esercizio otteniamo i 4 punti:
\begin{cases} (1,3) \\ (-1,3) \\ (1,-3) \\ (-1,-3) \end{cases}
Gli asintoti, proprio come prima, sono le due rette che passano per i vertici opposti del rettangolo che si è formato. Proprio come segue.
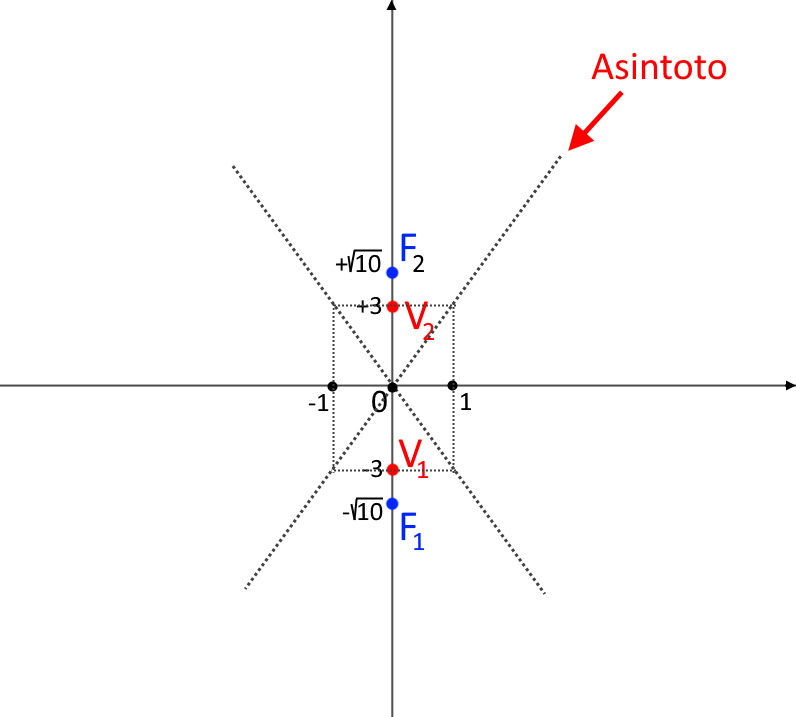
Abbiamo tutte le informazioni per disegnare l’iperbole: partendo da un vertice fate tendere agli asintoti la funzione, senza mai farla toccare. Si otterrà un grafico di questo tipo!
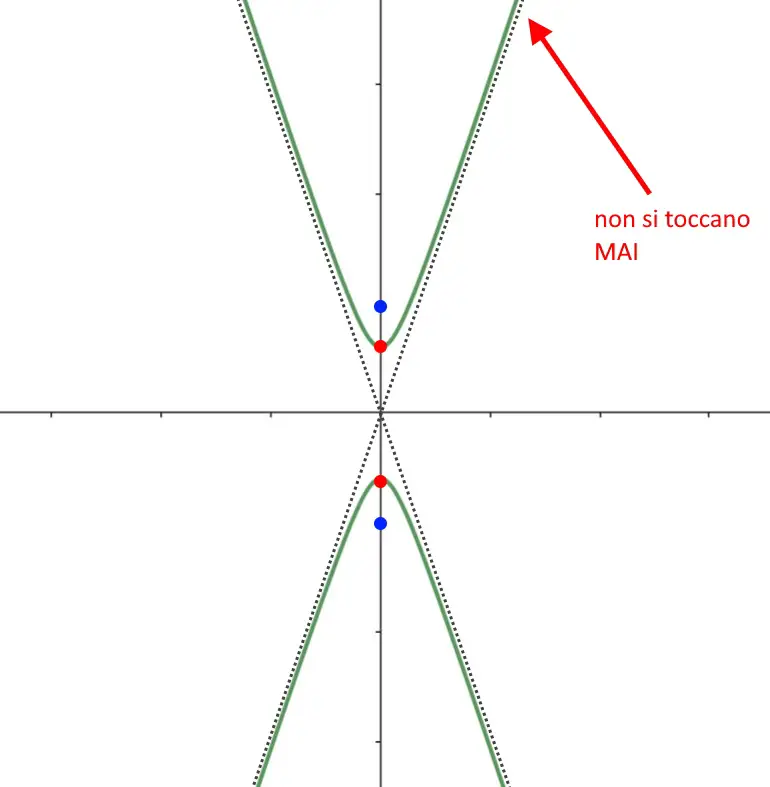
Anche qui stesso discorso di prima: vi basta memorizzare i 3 esercizi di questa pagina per saper disegnare una qualsiasi iperbole! Adesso vediamo l’ultimo caso: come disegnare un iperbole equilatera.
Come fare grafico di un iperbole equilatera
Un iperbole equilatera significa un iperbole semplicemente che ha il coefficiente a=b. Possiamo quindi avere una iperbole equilatera con fuochi sull’asse x, o un iperbole equilatera con fuochi sull’asse y.
Lo svolgimento dell’esercizio del grafico di un iperbole equilatera si rifà dunque ai due esercizi già fatti, con l’unica differenza che nelle formule avete un solo coefficiente, visto che a=b. Inoltre il calcolo degli asintoti non serve…vedremo il perché nel prossimo esercizio.
Esercizio 3. Disegnare il grafico dell’iperbole di equazione x^2 - y^2 = -2 .
Per ricavare la forma classica di un iperbole, come sempre, dividiamo semplicemente per 2 (non per -2 altrimenti verrebbero coefficienti negativi):
\frac{x^2}{2} - \frac{y^2}{2} = - 1
Quindi come potete vedere i due coefficienti sotto la x e la y sono uguali, ossia:
a^2 = b^2 = 2
Di conseguenza i due coefficienti sono:
a = b = \pm \sqrt{2}
E quindi è il caso di un iperbole equilatera! Inoltre dal coefficiente -1 a destra capiamo anche che è un iperbole con fuochi sull’asse y (caso visto nella sezione precedente).
Il procedimento quindi è esattamente lo stesso! L’unica cosa che vedremo dopo che cambia sono gli asintoti. Quindi proprio come sempre fatto, andiamo a calcolare le coordinate dei due vertici. Utilizziamo le formule dell’iperbole con fuochi sull’asse y.
V_1 = (0,-b) \implies V_1 = (0,-\sqrt{2})
V_2 = (0,+b) \implies V_2 = (0, +\sqrt{2})
Segniamo questi due vertici nel piano cartesiano. Adesso passiamo al calcolo dei due fuochi:
F_1 = (0,-\sqrt{a^2 +b^2}) \implies F_1 = (0,- \sqrt{2+2} ) = (0,-2)
F_2 = (0,+\sqrt{a^2 +b^2}) \implies F_2 = (0,+\sqrt{2+2} ) = (0,+2)
Come potete notare il valore di a e b è uguale…
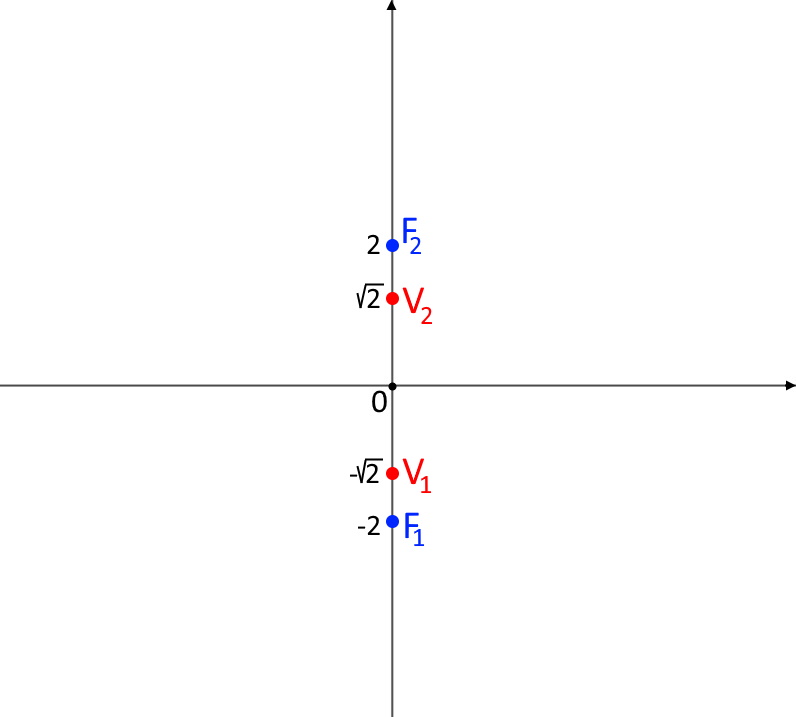
Adesso viene la parte diversa: gli asintoti non c’è bisogno di fare nessun calcolo. Essendo i due coefficienti uguali si formerebbe un quadrato sempre, qualsiasi siano i coefficienti. Di conseguenza per qualsiasi iperbole equilatera gli asintoti sono sempre le bisettrici dei quadranti, ossia le rette:
\begin{cases} y=x \\ y= -x \end{cases}
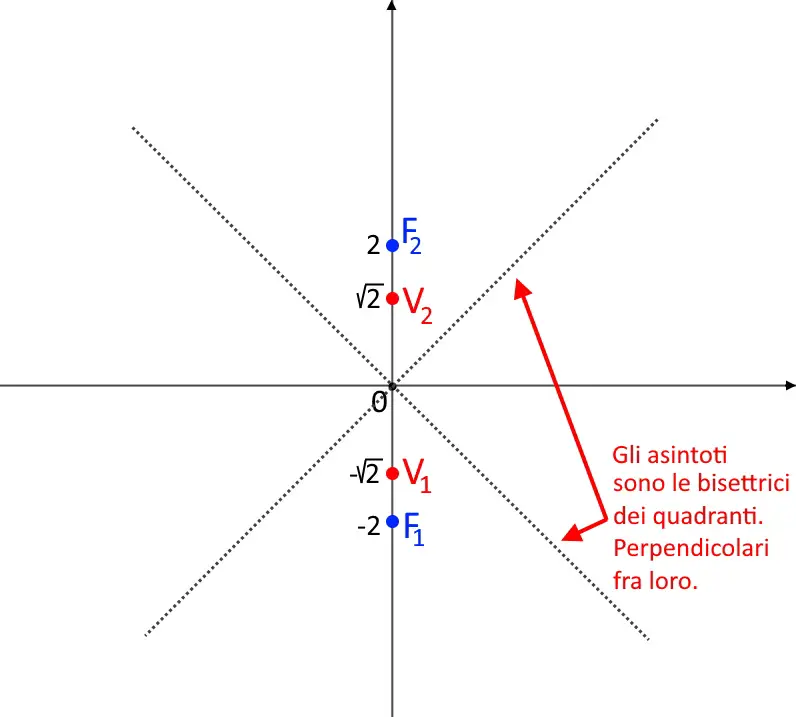
A questo punto disegniamo subito l’iperbole: non ci serve nient’altro. Come sempre partiamo dal vertice e andiamo a far tendere la funzione verso gli estremi degli asintoti. Otteniamo un grafico come quello seguente.
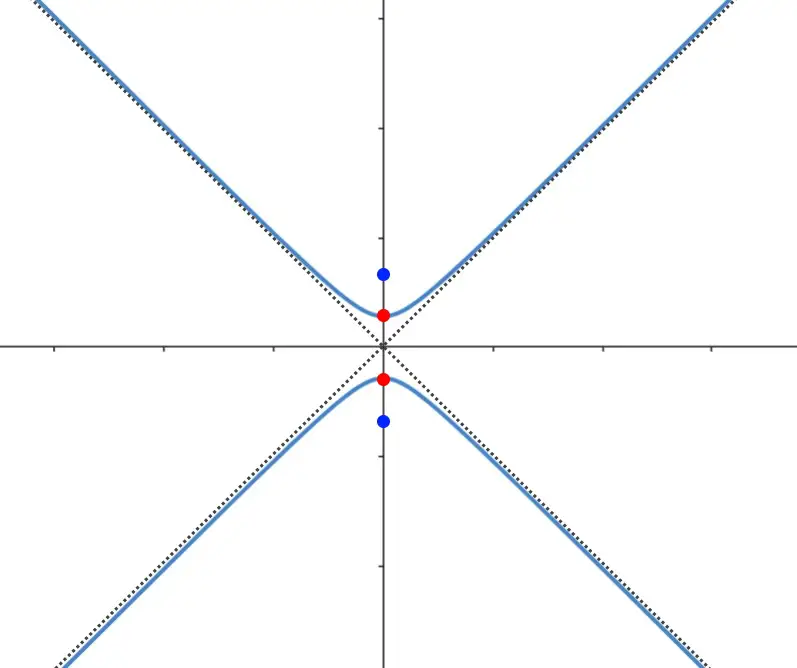
Abbiamo visto in questa pagina i tre casi principali che vi possono capitare per quanto riguarda il come disegnare un iperbole. Trovate comunque altre centinaia di esercizi svolti sia di matematica che di altro ancora!
Sostenete il sito!
Per approfondire:
https://it.wikipedia.org/wiki/Iperbole_(geometria)
equilatera