Vertice della parabola: formula, come calcolarla ed esempi
In questa pagina vedremo tutto sul vertice della parabola: come calcolarla, come trovarla e disegnarla, le formule da utilizzare e vari esempi. Alla fine vedremo poi degli esercizi svolti sul calcolo del vertice, in tutte le diverse tipologie di parabola.
Indice
Saper calcolare le coordinate del vertice è fondamentale, perché è la prima cosa che si fa quando si disegna una parabola, ad esempio. Quindi cominciamo subito!
Formule del vertice della parabola
Prima di addentrarci nelle formule dobbiamo comprendere alcune cose: esistono diversi tipi di parabole, di conseguenza ogni tipo di parabola avrà una formula diversa per trovare il vertice. In questa sezione mostreremo tutte le tipologie di parabole, e di vertici quindi. Prima di iniziare: che cos’è un vertice? Il vertice di una parabola è l’estremo interno del grafico della parabola. E’ dove “nasce” la parabola. Ora, partiamo dal vedere le formule nel caso più semplice di tipologia di parabola:
Parabola con vertice in origine ed asse coincidente con l’asse y
Non facciamoci spaventare dal nome molto lungo: basta leggere bene il nome per capire di che parabola si tratta. Essa è una parabola (quindi con forma di parabola appunto), con il suo vertice posizionato nell’origine degli assi cartesiani, ed avente asse che è proprio l’asse y.
Di conseguenza non c’è una formula per trovare il vertice di tale tipologia di parabola: il vertice è sicuramente posizionato nel punto di coordinate (0,0)!
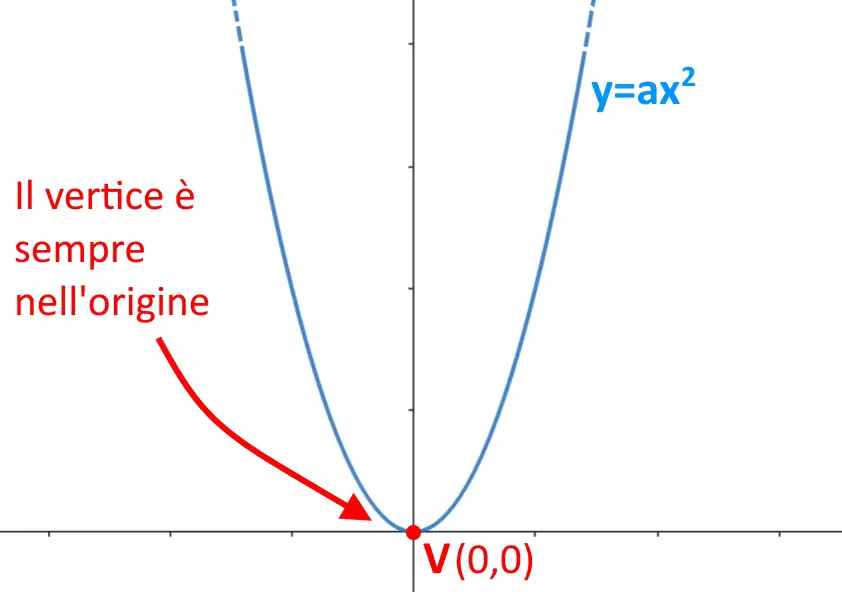
Quindi quando avete a che fare con una equazione di questo tipo:
Allora sapete che si tratta di questo tipo di parabola, e che il vertice è per forza in (0,0)!
Parabola con asse parallelo all’asse y
Come dice stesso la frase: questa tipologia rappresenta una parabola con asse parallelo ad y, e di conseguenza asse verticale in pratica! Mentre del vertice non dice nulla, di fatti il vertice varia a seconda dell’equazione.
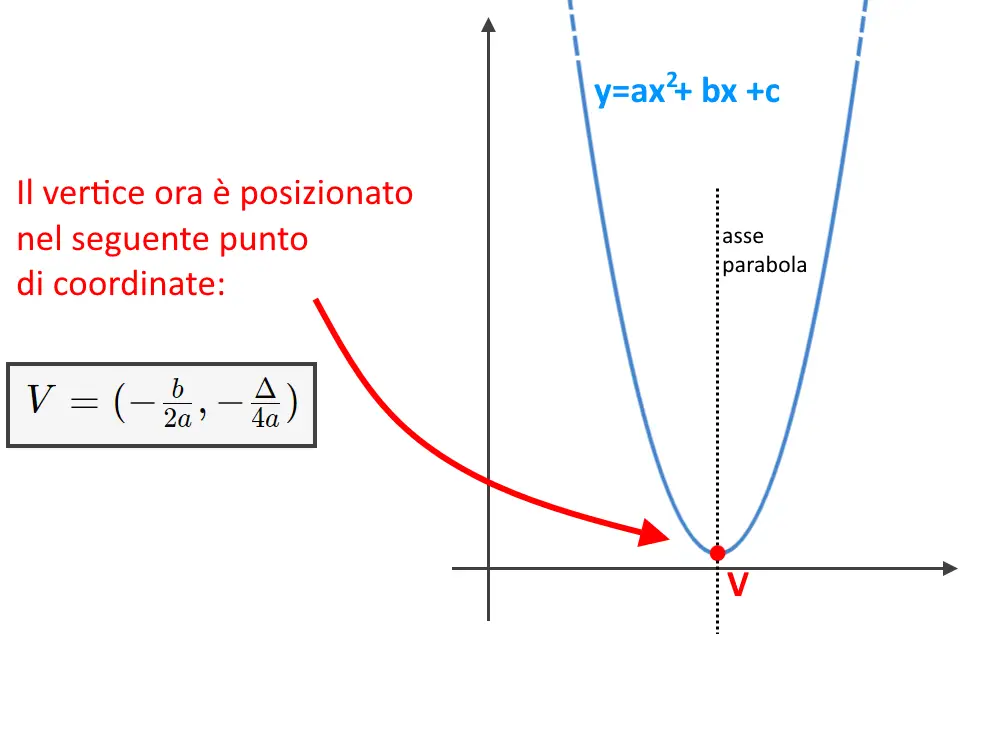
L’equazione di questo tipo di parabola è:
Questo ci ricorda una equazione di secondo grado!
Il posizionamento del vertice è legato al valore dei coefficienti a,b ed c. La formula per calcolare il vertice è in questo caso:
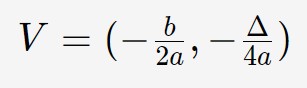
Quindi, per conoscere il vertice di questa parabola, abbiamo bisogno di tutti e tre i coefficienti, nessuno escluso!
Come vedete il è proprio quello che si usa quando si deve risolvere una equazione di secondo grado!
Curiosità: se provate a graficare una equazione di secondo grado, vi verrà fuori una parabola. Ecco spiegato la presenza di quel !
Parabola con asse parallelo all’asse x
Cosa è cambiato rispetto a prima? Se prima avevamo una parabola disposta in verticale con vertice in giro nel piano cartesiano, adesso la parabola è messa in orizzontale (con asse orizzontale).
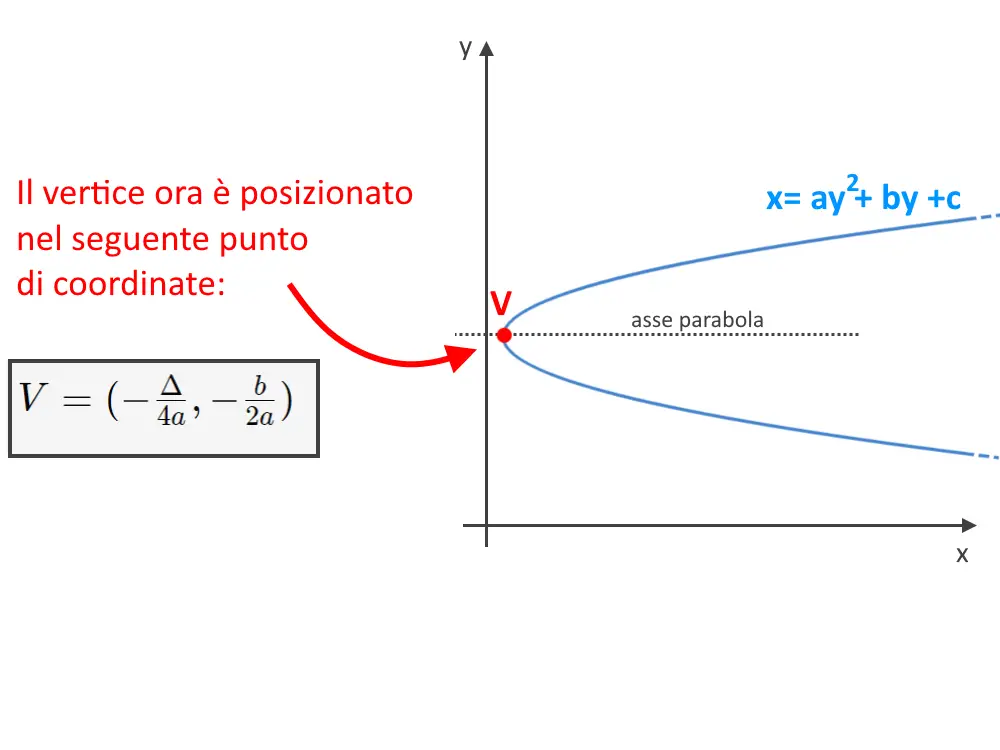
Analogamente a prima, il vertice è legato ai coefficienti dell’equazione. Una parabola di questa tipologia ha l’equazione che è della forma:
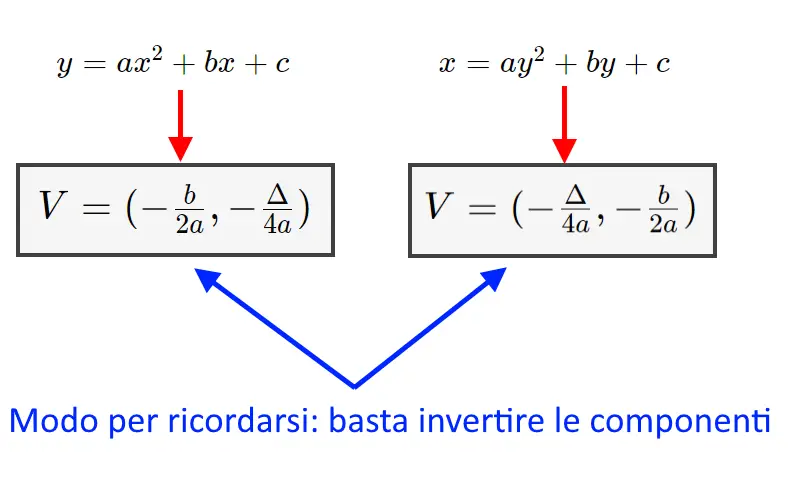
Per ricordarvi: basta scambiare x e y in pratica
E questo lo si eredita nella formula del vertice: basta scambiare le componenti della formula del caso precedente per ottenere questa nuova formula del vertice:
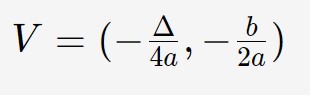
Osservate: l’equazione ha x ed y scambiati rispetto a prima la formula del vertice ha la componente x scambiata con quella y, sempre rispetto a prima!
Questi sono tutti trucchetti per non riempirci la testa di inutili formule, bisogna essere furbi!
Ora che sappiamo quali sono le formule da utilizzare, passiamo alla pratica: vediamo degli esercizi svolti e spiegati.
Come calcolare e trovare il vertice di una parabola
Di seguito, riassumiamo il procedimento che faremo per calcolare e trovare il vertice di qualsiasi parabola.
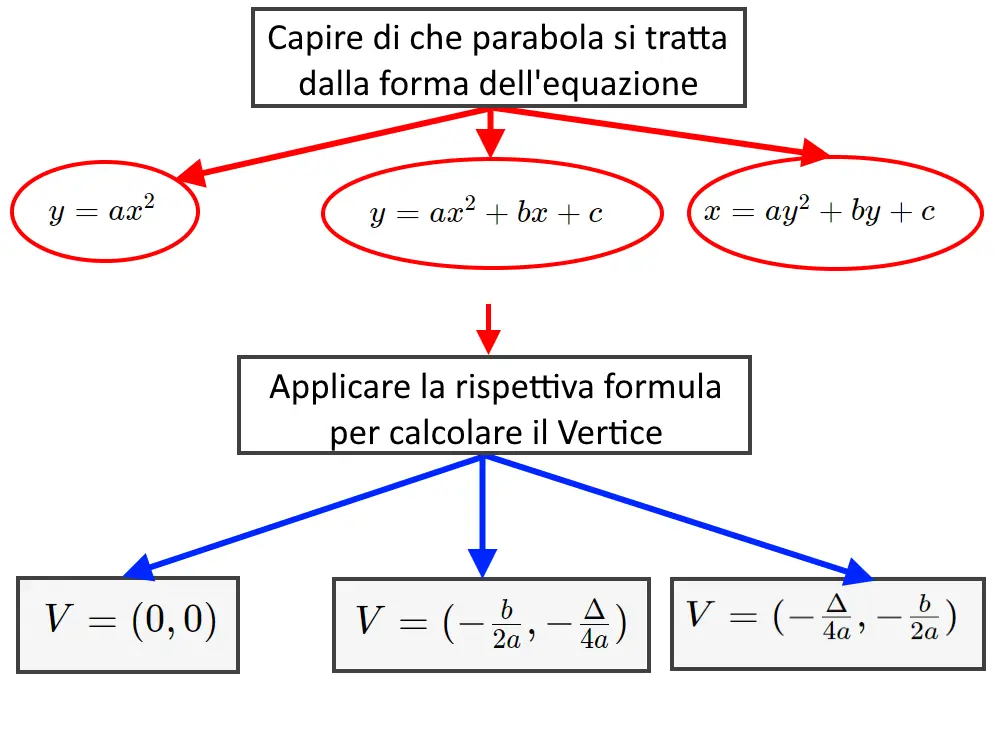
Esempio 1. Determinare le coordinate del vertice di una parabola di equazione .
Osserviamo prima di tutto l’equazione che ci dà, perché da questa capiamo la tipologia di parabola. E’ evidente che si tratta del primo caso, ossia di una parabola con equazione della forma:
E di conseguenza il vertice è sicuramente nell’origine, ossia nel punto (0,0). Le coordinate del vertice sono quindi e .
Esempio 2. Determinare le coordinate del vertice di una parabola di equazione .
Questa equazione è sempre riferita ad una della forma:
Di fatti non confondetevi: anche se abbiamo -7, il coefficiente a può assumere tutti i valori, anche quelli negativi! Ovviamente tranne a=0, altrimenti sarebbe y=0…ossia una funzione sempre nulla.
Quindi anche in questo caso il vertice è in (0,0)!
Esempio 3. Calcolare il vertice di una parabola che ha per equazione .
Come prima cosa: osserviamo l’equazione. Capiamo immediatamente che si tratta di una parabola con asse parallelo ad y, di conseguenza dobbiamo utilizzare la formula del vertice relativa a tale tipologia:
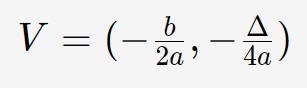
Dalla formula capiamo che ci serve a,b e poi . I primi due coefficienti li capiamo per confronto dall’equazione. Di fatti guardate:
E capiamo subito chi sono a ed b! Scriviamo poi in maniera ordinata ciò che ci serve.
Ci serve il delta. Il delta si calcola come se fosse una normale equazione di secondo grado:
Per la parabola non fa niente che il , non è un problema!
Sostituiamo nella formula per calcolare le componenti del vertice:
E quindi, semplificando numeratore e denominatore:
Ed i giochi sono fatti!
Esempio 4. Trovare il vertice di una parabola con equazione .
Questa invece è una parabola con asse parallelo ad x, quindi disposta in maniera orizzontale. Vediamo la formula che ci serve:
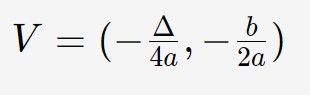
E’ la stessa di prima, ma con componenti inverse! (è un modo per ricordarsela)
Per confronto capiamo il valore dei coefficienti. Scriviamo poi in maniera ordinata ciò che ci serve:
Anche qui si ha che:
Inseriamo nella formula i vari corrispondenti dati.
Semplificando otteniamo che il vertice è posizionato nel piano cartesiano in:
State sempre attenti ai segni, quando ci sono due meno consecutivi!
Esempio 4. Una figura geometrica è rappresentata dall’equazione . Rappresenta una parabola? Di che tipo? Se sì trovare il suo vertice.
Allora, potrebbe sembrare un’altra cosa, ma in realtà è una parabola. Di fatti se lasciamo a sinistra solo la y otteniamo:
E questa ci ricorda una parabola con asse parallelo ad y, della forma:
Notiamo però che b=0… e ciò non è un problema! L’importante è che , poi gli altri coefficienti possono essere quello che vogliono!
Quindi usiamo sempre:
Calcoliamo il delta come sempre:
Sostituiamo nella formula ed abbiamo fatto!
La prima frazione fa zero, la seconda la si semplifica:
La pagina è conclusa, speriamo vi sia stato chiaro tutto!
Trovate altri centinaia di argomenti di Matematica, Geometria Analitica e Geometria!
Continuate a supportare il nostro sito!
equazione
esempi
parabola
calcolo