Asintoti dell’iperbole: formule ed esempi spiegati
In questa pagina vedremo cosa sono gli asintoti di un iperbole, come trovarli e come disegnarli. Inoltre vedremo cosa significano, e perché sono importanti soprattutto per poi trovare il grafico di un iperbole.
Indice
- Cosa sono gli asintoti di un iperbole?
- Come calcolare gli asintoti dell’iperbole
- Come disegnare gli asintoti di una qualsiasi iperbole
- Asintoti iperbole equilatera
Cominciamo subito!
Cosa sono gli asintoti di un iperbole?
L’iperbole è una figura geometrica che può essere rappresentata con un grafico in un piano cartesiano. Esso è un grafico un po’ particolare per via della presenza di asintoti obliqui, cui fra poco arriveremo! Questa seguente è un iperbole.
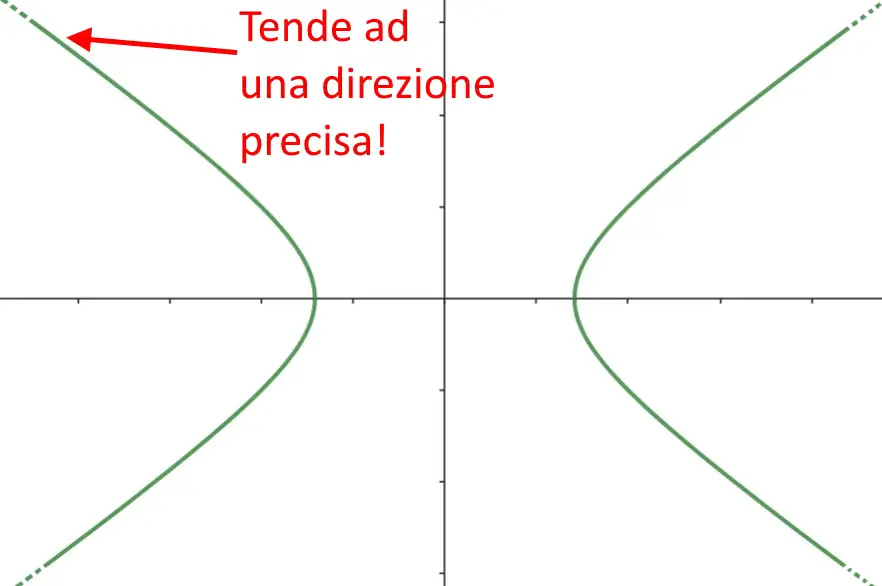
Come possiamo notare, il grafico agli estremi (ossia a destra a tutto e a sinistra a tutto) segue una linea ben precisa.
Un iperbole segue delle direzioni precise, date dalla presenza di asintoti! Ma cosa sono gli asintoti? Gli asintoti sono delle linee rette immaginarie cui il grafico tende. Un iperbole possiede degli asintoti, perché agli estremi tende ad assumere un certo valore, seguendo proprio la direzione di queste linee rette! Una caratteristica importante di un asintoto è che: il grafico di una funzione non tocca mai un asintoto! I due si avvicinano sempre di più, ma non arriveranno mai al punto di toccarsi.
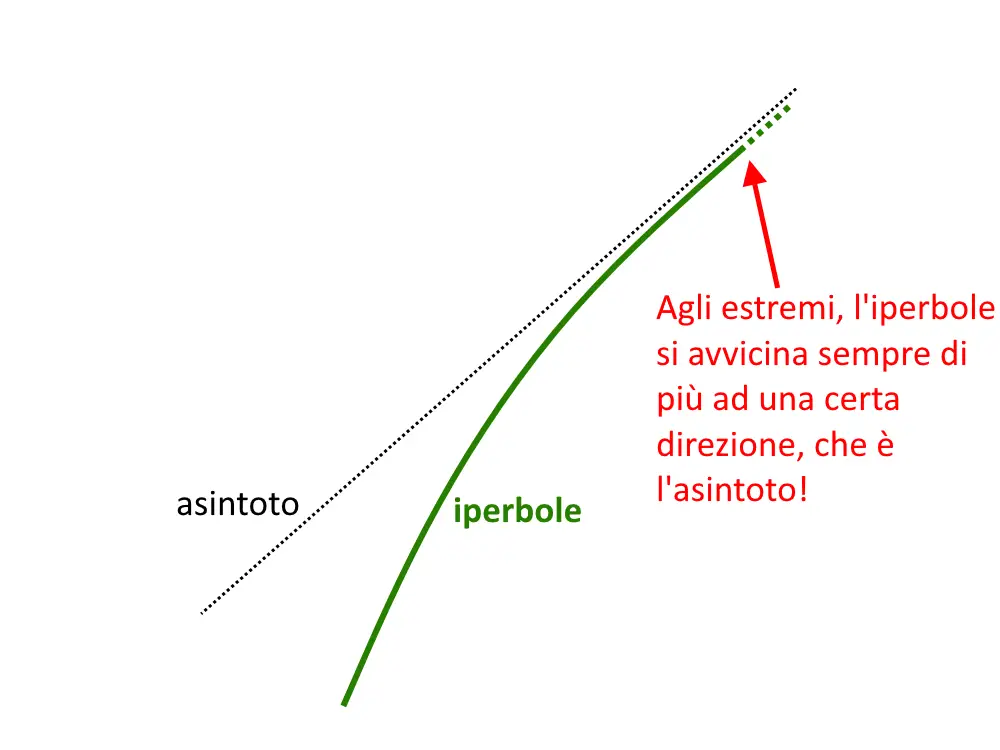
Gli asintoti possono essere delle linee verticali, orizzontali o oblique. Un iperbole possiede degli asintoti obliqui, ossia con direzione obliqua. E per di più, un iperbole possiede ben due asintoti!
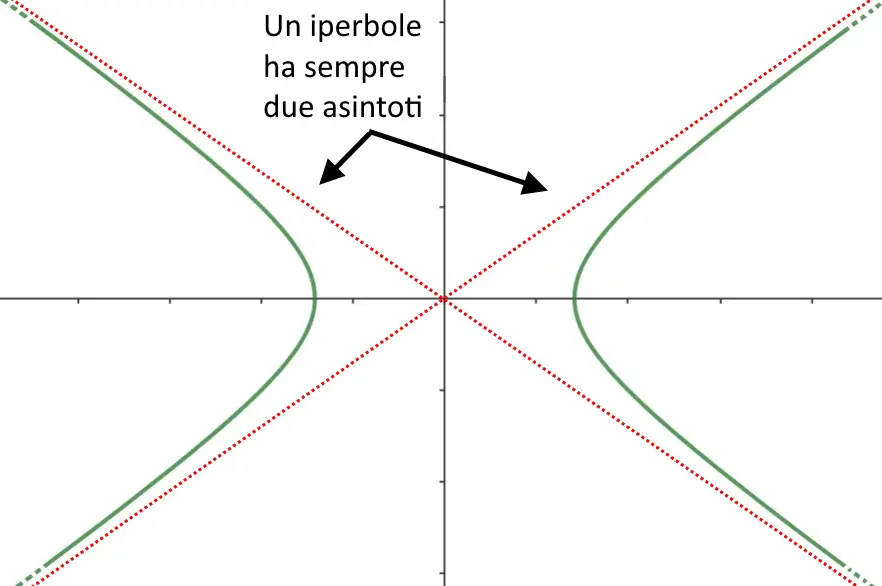
Sappiamo che l’iperbole può avere i fuochi sull’asse x, sull’asse y, o essere equilatera. Vediamo alcuni esempi degli asintoti di queste diverse tipologie di iperboli.
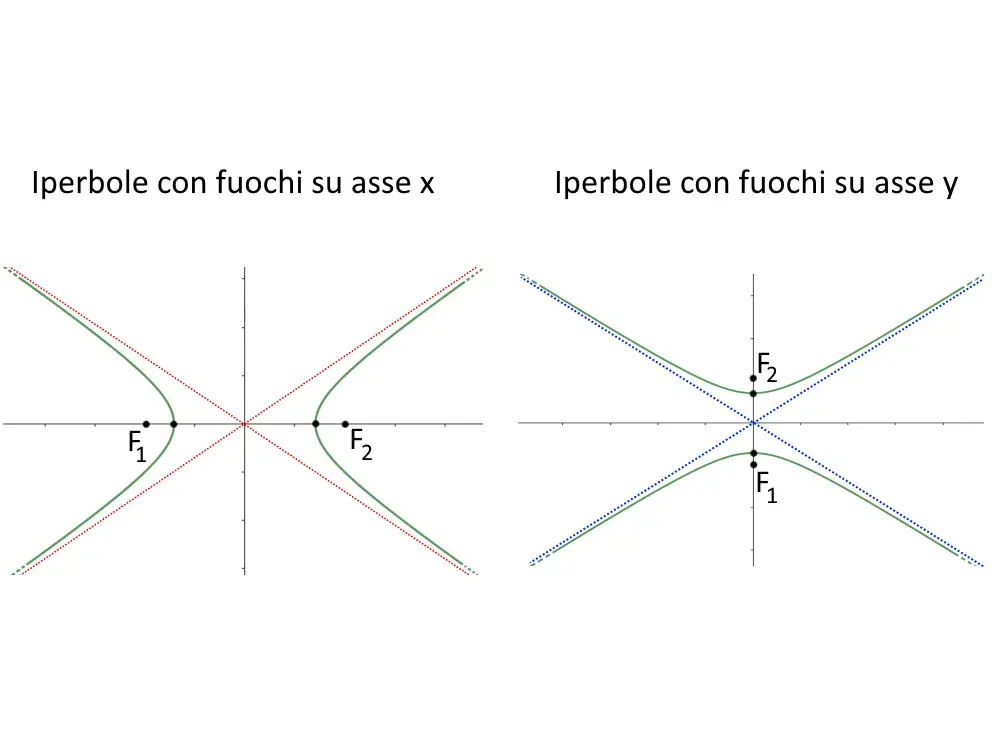
Ora che abbiamo capito il significato dell’asintoto. Cerchiamo di capire come calcolare e come trovare questi asintoti!
Come calcolare gli asintoti dell’iperbole
Ora che abbiamo capito cosa è un asintoto (una linea retta immaginaria cui il grafico tende), come facciamo a calcolarlo e quindi a trovarlo? Qui si tratta semplicemente di imparare delle formule, nulla di più.
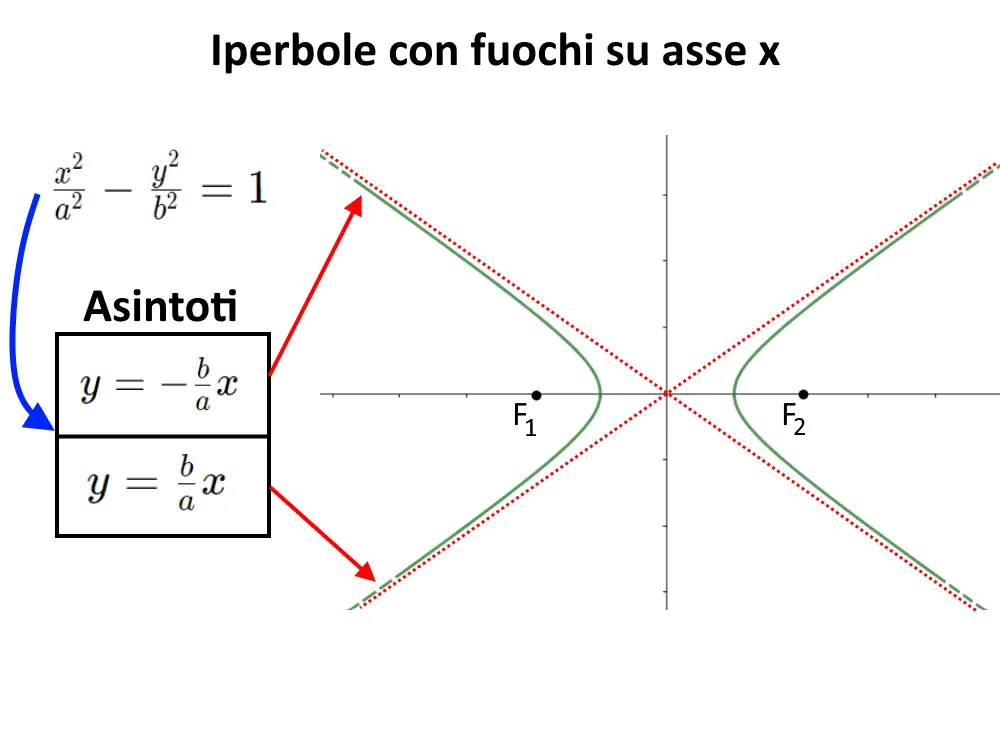
Consideriamo il caso di un iperbole con fuochi sull’asse x, di equazione:
\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1
Gli asintoti di questo tipo di iperbole sono due, e sono date dalle seguenti formule:
y= \frac{b}{a} x
y= - \frac{b}{a}x
E di fatti hanno la forma di equazioni di rette in un piano cartesiano! Quindi a seconda dei valori di a e di b, tali rette possono assumere diverse angolazioni!
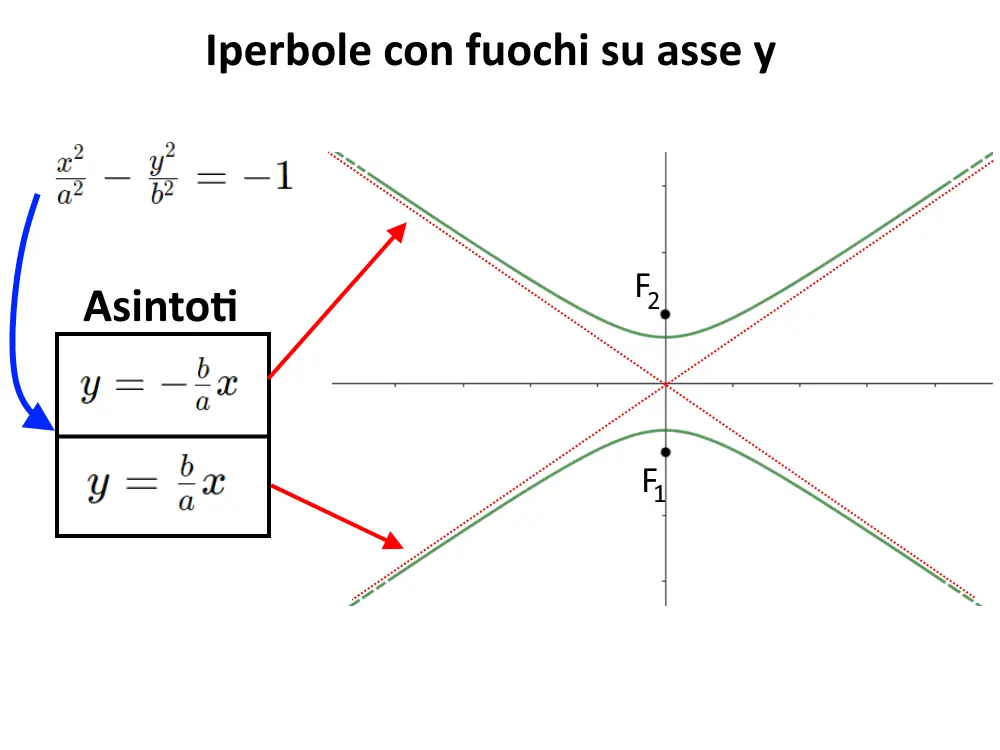
Consideriamo adesso invece il caso di un iperbole con fuochi sull’asse y, con equazione:
\frac{x^2}{a^2} - \frac{y^2}{b^2} = -1
Gli asintoti di questo tipo di iperbole sono sempre due, e sono date dalle stesse formule. Cambia quindi solamente la disposizione del grafico.
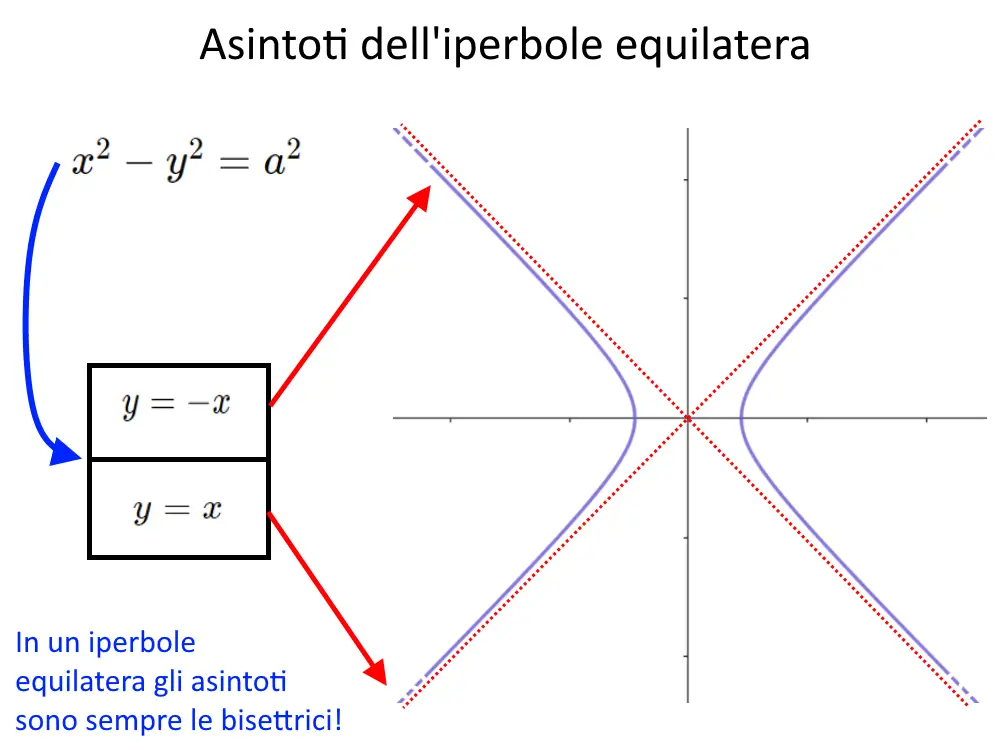
Per un iperbole equilatera il discorso è molto più semplice. Gli asintoti sono sempre gli stessi, visto che in un iperbole a^2 = b^2 . Di conseguenza abbiamo che, per qualsiasi equazione, l’iperbole equilatera ha come asintoti:
y=x
y=-x
Ossia le bisettrici del primo-terzo quadrante e del secondo-quarto quadrante.
Ora che conosciamo le formule, e come calcolare le equazioni degli asintoti obliqui di un iperbole, come facciamo a disegnarle precisamente?
Come disegnare gli asintoti di una qualsiasi iperbole
Ci sono due modi per disegnare gli asintoti dell’iperbole:
- Disegnare un quadrato usando i coefficienti a e b
- Prendere un punto qualsiasi di ogni asintoto e disegniamo la retta;
Vi diciamo già che forse il primo è il più comodo!
Disegnare un quadrato usando i coefficienti a e b
Consideriamo un iperbole di equazione:
\frac{x^2}{4} - \frac{y^2}{16} = 1
Capiamo, dalla forma dell’equazione, che è un iperbole con fuochi sull’asse x. Per procedere al disegno degli asintoti in maniera molto naturale e semplice, troviamo prima i coefficienti a e b:
a=2, \; b= 4
Disegniamo sull’asse x i punti -a e +a, ossia (-2,0) e (2,0). (Il coefficiente a è relativo alla x)
Poi disegniamo sull’asse y i punti -b e +b. Cioè semplicemente (0,-4) e (0,4).
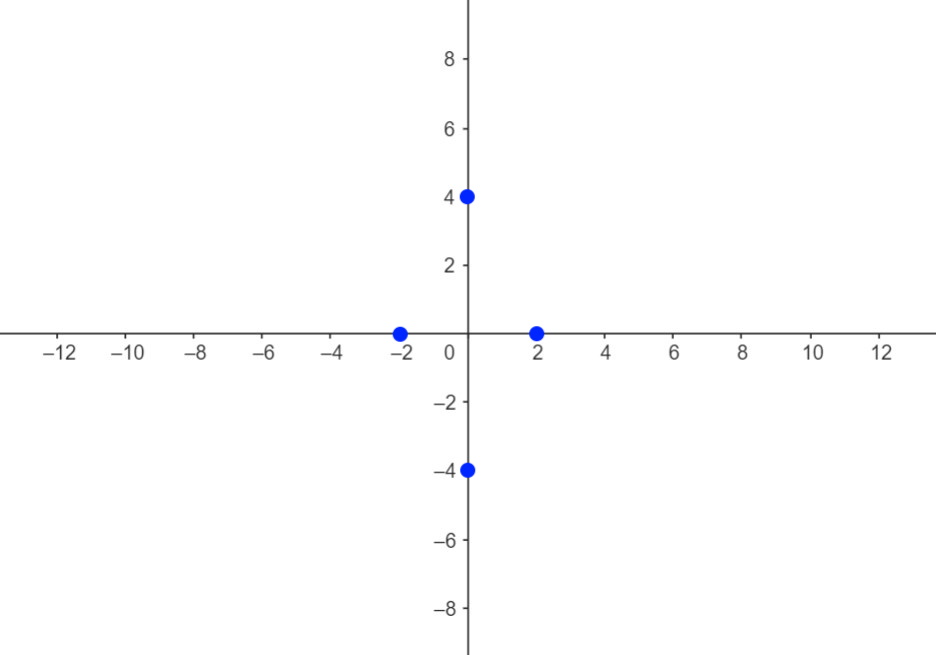
A questo punto formiamo un quadrato tratteggiato, come segue.
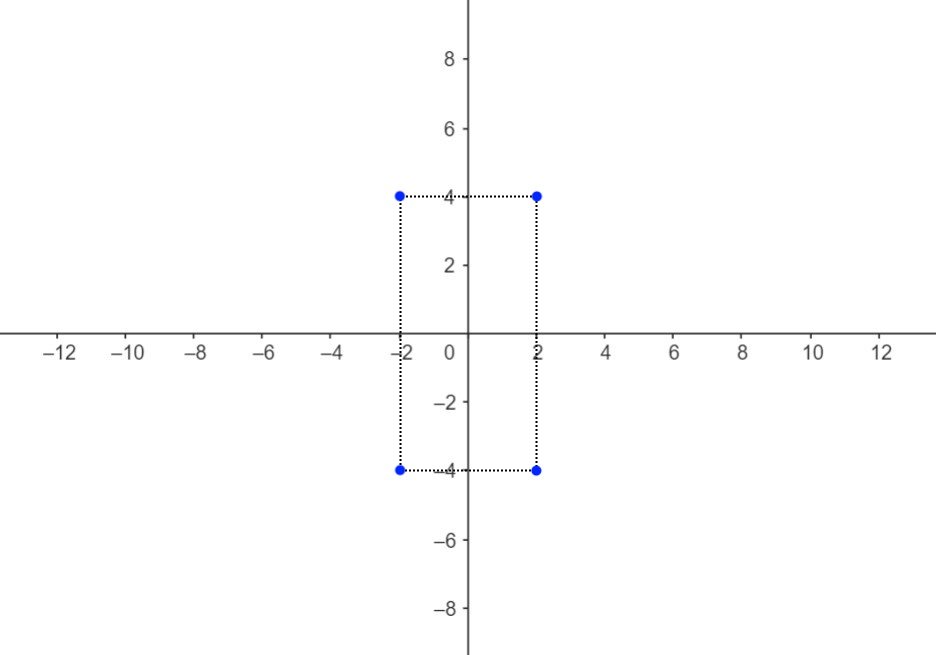
Ed ora non ci rimane altro che disegnare i due asintoti, che passano per due vertici opposti del quadrato!
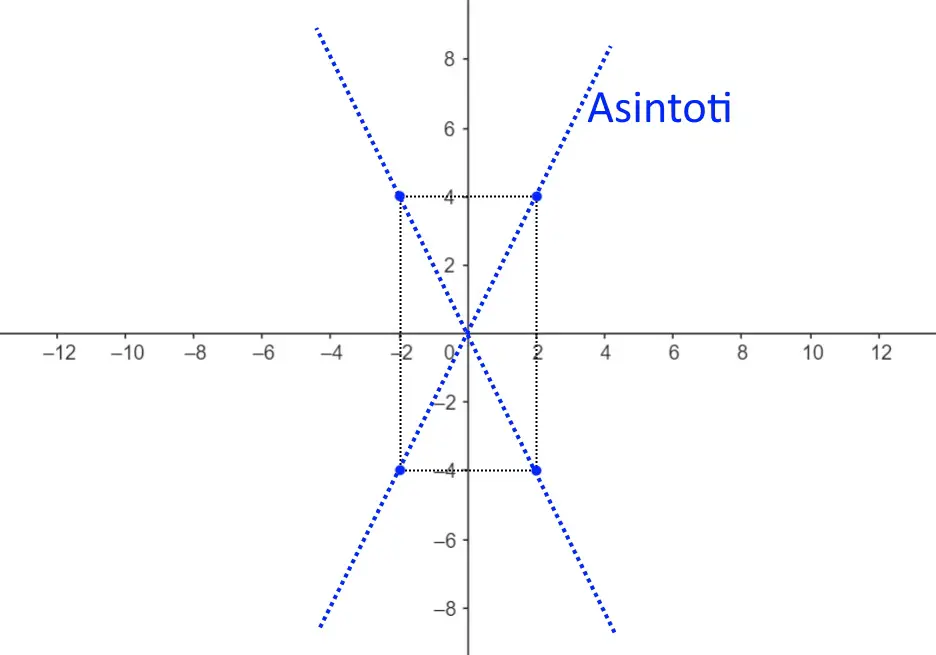
Questa è una procedura molto più “grafica”, ed intuitiva, ed è la migliore a mio parere. Questo ricordiamo essere fondamentale per disegnare poi l’iperbole. Il prossimo metodo è più calcoloso.
Prendere un punto qualsiasi di ogni asintoto e disegniamo la retta
Consideriamo un iperbole di equazione seguente:
\frac{x^2}{9} - \frac{y^2}{4} = 1
Capiamo (dal fatto che c’è un numero positivo a destra) che è un iperbole con fuochi sull’asse x. Ricordiamo che le formule degli asintoti suoi sono:
y= \frac{b}{a} x
y= - \frac{b}{a}x
Dall’equazione capiamo che a=3 e che b=2. Di conseguenza gli asintoti sono precisamente:
y= \frac{2}{3} x
y= - \frac{2}{3}x
Adesso vogliamo disegnarli nel piano cartesiano. Prendiamo un punto qualsiasi della retta relativa al primo asintoto, per esempio:
x=1 \implies y=\frac{2}{3}
Visto che gli asintoti, a causa della loro equazione, passano sicuramente per l’origine, passeranno allora anche per il punto (0,0). Disegniamo quindi questi due punti. Poi tracciamo una retta che passa fra questi due punti.
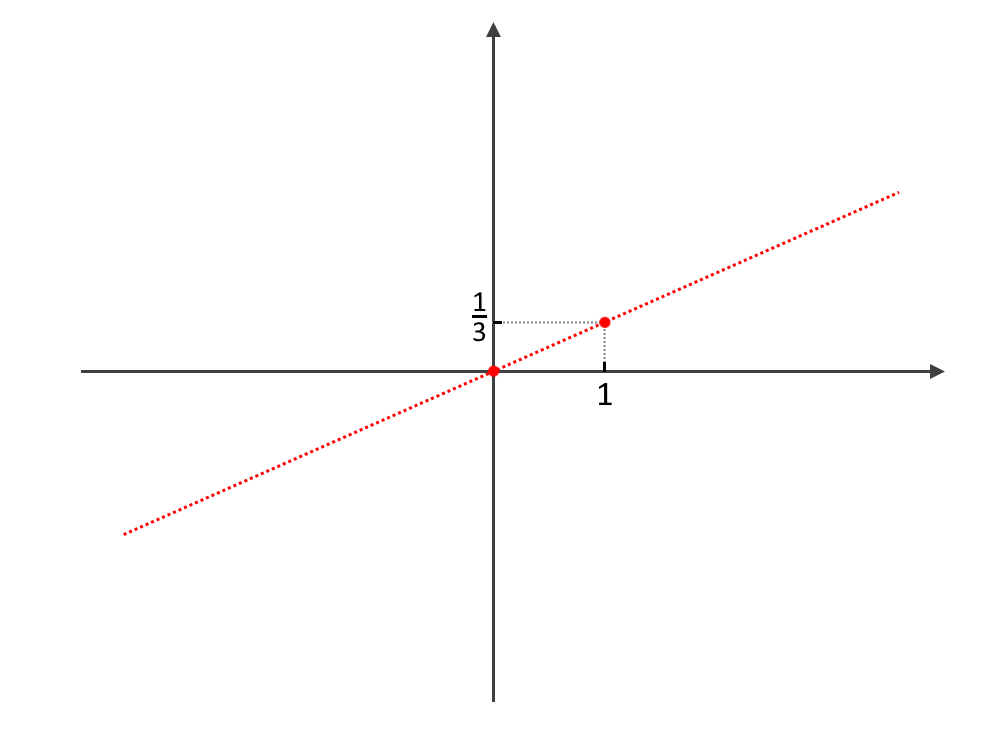
Facciamo lo stesso anche con il secondo altro asintoto, prendendo x=-1 questa volta, per comodità:
x=-1 \implies y=-(-\frac{2}{3}) = \frac{2}{3}
E di fatti per via della simmetria otteniamo un punto con stessa altezza. I due asintoti disegnati risultano perciò i seguenti.
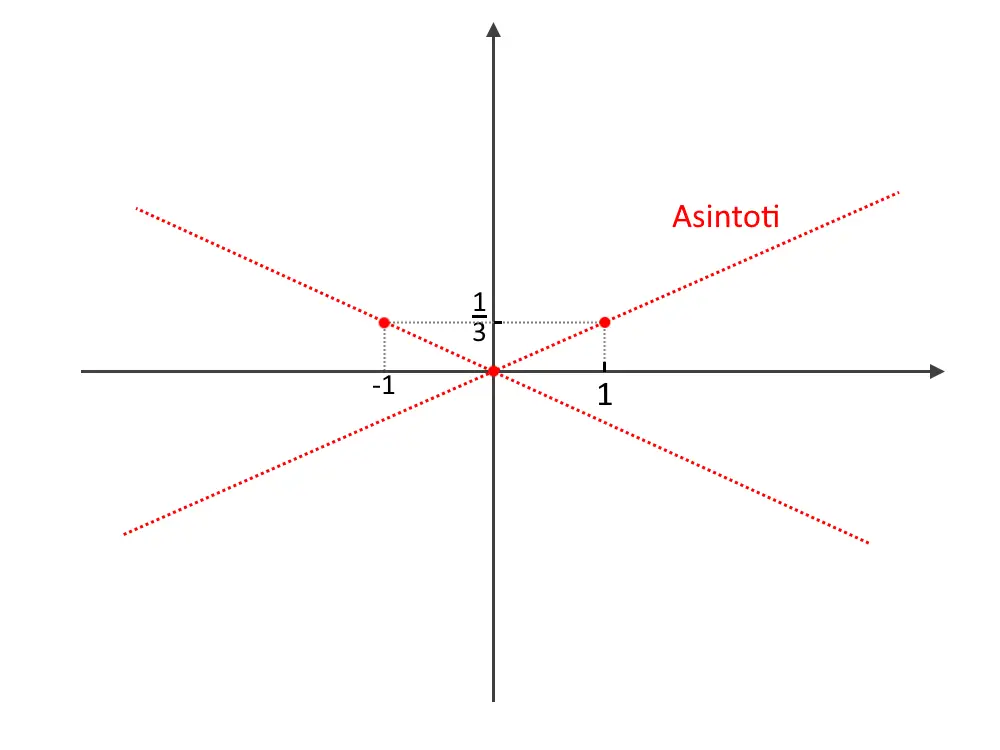
Speriamo che questi due metodi vi siano stati chiari! (Usate il primo)
La pagina è conclusa, speriamo che vi stato chiaro tutto, se avete domande potete sempre chiedere all’email del sito!
Trovate altri centinaia di argomenti ed esercizi svolti di matematica, geometria analitica e geometria!
Continuate a supportare il sito!
formule
equilatera