Iperbole equilatera: equazione, asintoti, disegno ed esempi
In questa pagina ci concentriamo sull’iperbole equilatera: ne vedremo l’equazione, come trovare gli asintoti. Vedremo inoltre come fare il grafico, e quindi come disegnarla, e poi alcuni esempi di esercizi svolti e spiegati con cura.
Indice
- Equazione dell’iperbole equilatera
- Formule dei fuochi e dei vertici
- Eccentricità dell’iperbole equilatera
- Asintoti dell’iperbole equilatera
- Come disegnare un iperbole equilatera
Senza perdere altro tempo, cominciamo subito!
Equazione dell’iperbole equilatera
L’iperbole equilatera può essere di due tipi:
- Equilatera con fuochi sull’asse x;
- Equilatera con fuochi sull’asse x.
Partiamo dalla prima. Ricordiamo che l’equazione di un iperbole con fuochi sull’asse x aveva come equazione:
\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1
Un iperbole qualsiasi, generica, è caratterizzata dall’avere i coefficienti a ed b generici, quindi in generale diversi. Questo si traduce in una iperbole con eccentricità qualsiasi, e quindi una curvatura qualsiasi.
Una iperbole equilatera con fuochi sull’asse x invece, presenta la stessa identica equazione, ma con una caratteristica in più:
a^2=b^2
I coefficienti sono uguali! Quindi otteniamo:
\frac{x^2}{a^2} - \frac{y^2}{a^2} = 1
A questo punto, possiamo rendere più semplice la forma di questa equazione, moltiplicando tutto per a^2 . Otteniamo così l’equazione di una iperbole equilatera con fuochi sull’asse x.
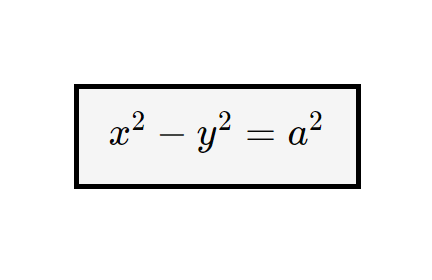
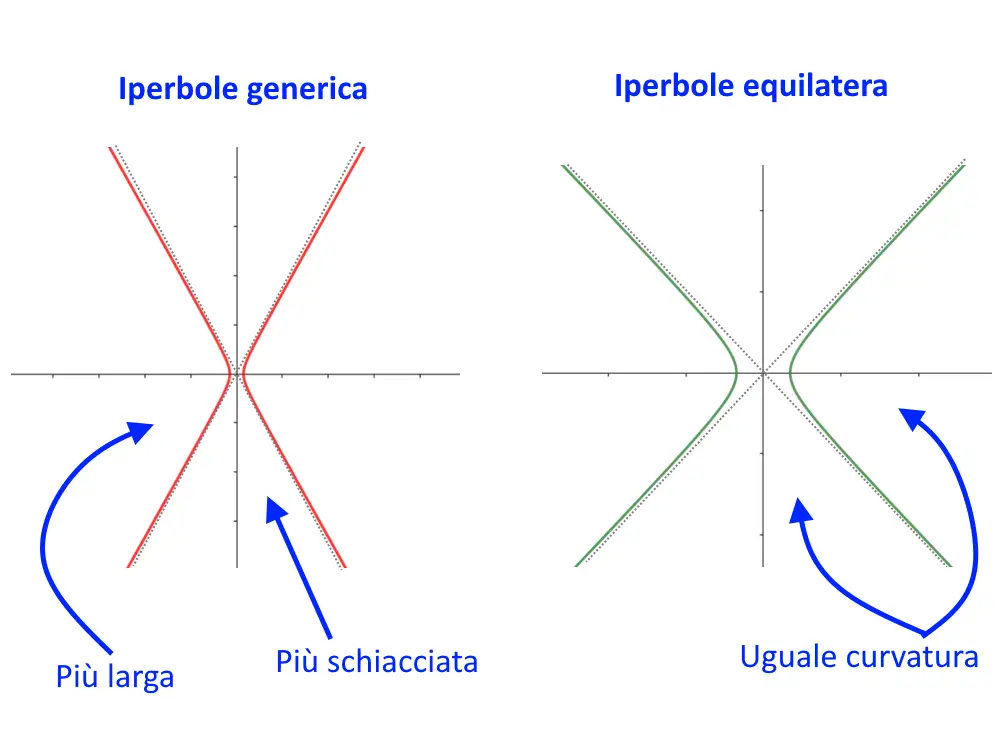
Qual è la conseguenza di avere i coefficienti uguali? Avere stessi coefficienti davanti alla x e alla y si traduce in un certa simmetria rispetto agli assi cartesiani. Guardate con i vostri occhi la differenza di una iperbole generica e di una equilatera!
E poi per ricavare l’equazione di una iperbole equilatera con fuochi sull’asse y, partiamo sempre dall’equazione dell’iperbole generica con fuochi sull’asse y:
\frac{x^2}{a^2} - \frac{y^2}{b^2} = -1
Seguiamo gli stessi passaggi di prima, quindi ripetiamo che equilatera vuol dire che i coefficienti sono uguali:
a^2=b^2
Quindi otteniamo:
\frac{x^2}{a^2} - \frac{y^2}{a^2} = -1
Moltiplichiamo tutto per a^2, e ricaviamo così l’equazione di una iperbole equilatera con fuochi sull’asse y.
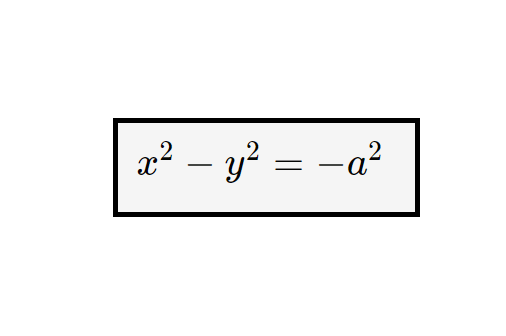
Vediamo adesso le formule dei fuochi e dei vertici come sono.
Formule dei fuochi e dei vertici
Le formule dei fuochi e dei vertici si rifanno alle iperboli normali, ma con l’aggiunta in più di avere i coefficienti uguali.
Per esempio, se la formula del fuoco di una iperbole generica con fuochi sull’asse x era:
F_1 = (-\sqrt{a^2 +b^2 },0), \; F_2 = (\sqrt{a^2 +b^2 },0)
Ma se i coefficienti sono uguali cosa succede? Per una iperbole equilatera, dove a ed b sono uguali, succede che:
F_1 = (-\sqrt{a^2 +a^2 },0), \; F_2 = (\sqrt{a^2 +a^2 },0)
F_1 = (-\sqrt{2a^2 },0), \; F_2 = (\sqrt{2a^2 },0)
E quindi:
F_1 = (-\sqrt{2}a ,0), \; F_2 = (\sqrt{2}a,0)
Con questi passaggi troviamo tutte le formule che ci servono, partendo da quelle generali. Riassumiamo nella tabella seguente tutte le formule dei fuochi e dei vertici per una iperbole equilatera.
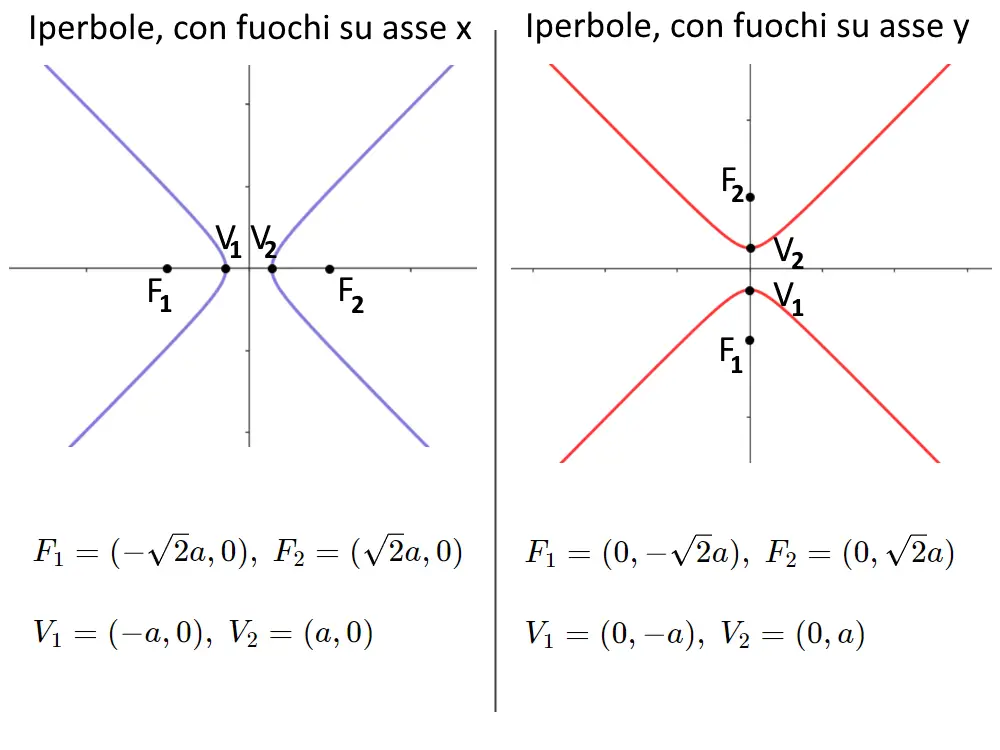
Ora che abbiamo introdotto le equazioni, passiamo ad approfondire il tutto. Vediamo adesso l’eccentricità.
Eccentricità dell’iperbole equilatera
Calcolare l’eccentricità è fondamentale per capire il significato di “equilatera”. La formula dell’eccentricità ricordiamo essere in un iperbole generica:
e = \frac{\sqrt{a^2 + b^2} }{a}
Ma nel caso di una iperbole equilatera, noi abbiamo i coefficienti uguali, ossia a^2 = b^2 , di conseguenza l’eccentricità risulterà essere:
e = \frac{\sqrt{a^2 + a^2} }{a}
e = \frac{\sqrt{2a^2} }{a} = \frac{\sqrt{2}a }{a} = \sqrt{2}
L’eccentricità è costante: è sempre la stessa in tutte le iperboli equilatere! L’eccentricità è una misura della curvatura, il che significa che la curvatura della funzione è sempre la stessa.
Nella immagine seguente abbiamo esempi di iperboli con diverse eccentricità.
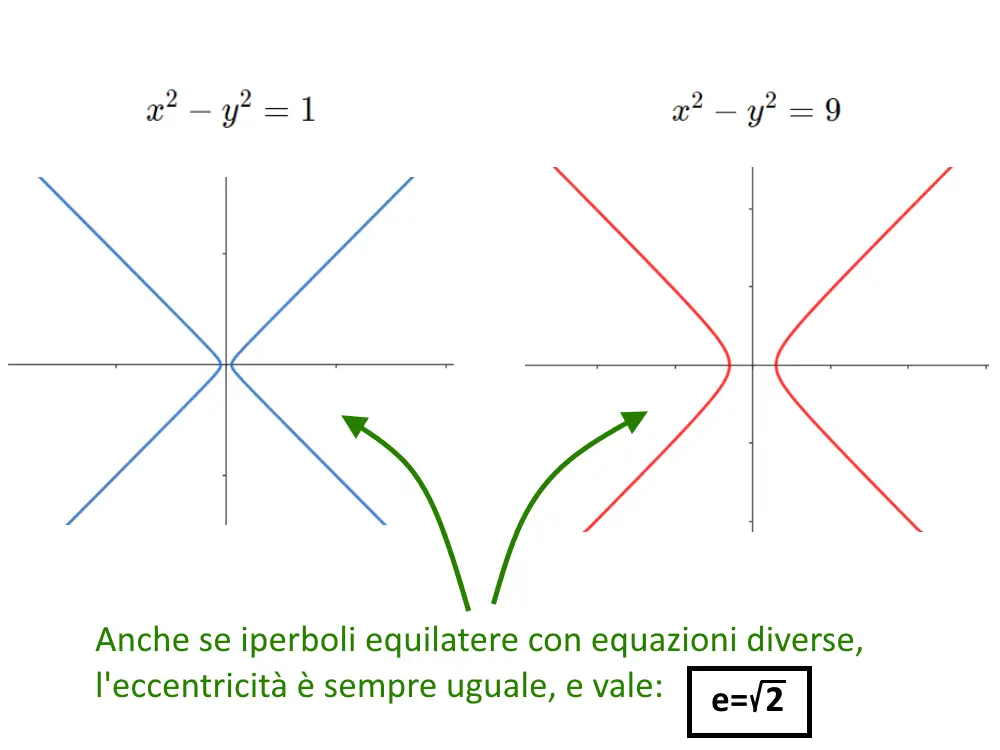
Questo visto fin ora ha anche un’altra conseguenza negli asintoti.
Asintoti iperbole equilatera
Abbiamo detto che l’eccentricità è costante, e quindi la curvatura è uguale. Questo è a causa del fatto che i coefficienti sono uguali. Il fatto che i coefficienti sono uguali hanno anche una conseguenza notevole negli asintoti.
Vediamo un attimo la formula generica degli asintoti in una qualsiasi iperbole:
y= \frac{b}{a} x \;\;\;\;\; y =-\frac{b}{a} x
Ma se i coefficienti sono uguali (a=b), allora significa che:
y= \frac{a}{a} x \;\;\;\;\; y =-\frac{a}{a} x
E quindi:
y= x \;\;\;\;\; y =- x
Ossia le bisettrici rispettivamente del primo-terzo quadrante e del secondo-quarto quadrante.
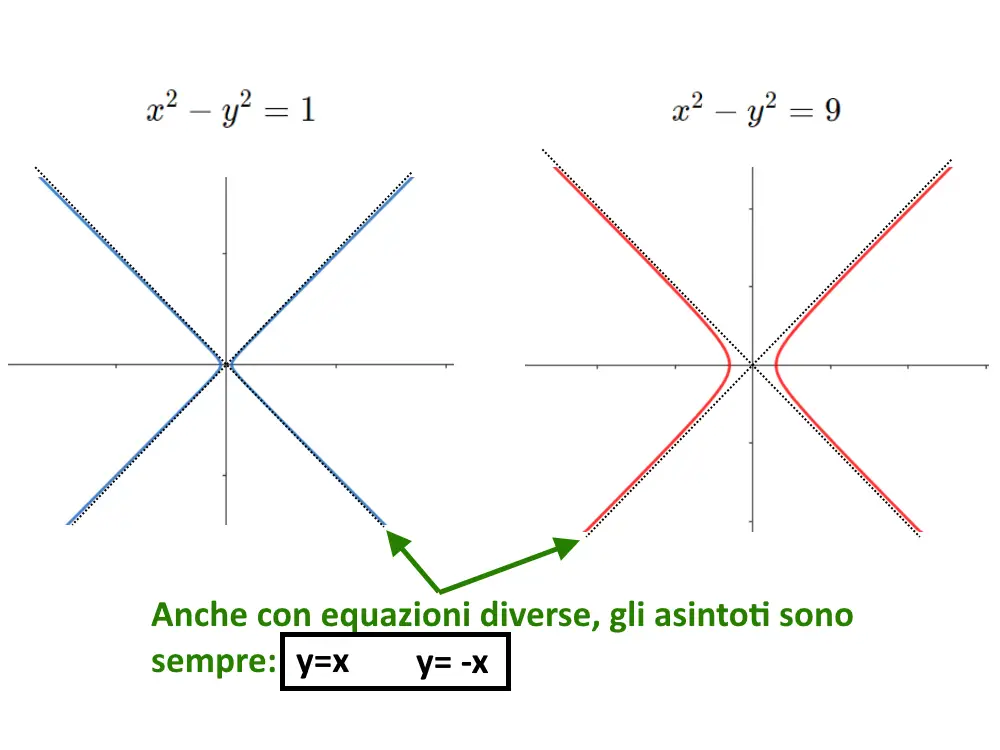
Anche gli asintoti sono sempre gli stessi: e sono proprio sempre le due bisettrici!
Come disegnare un iperbole equilatera
Esempio. Disegnare l’iperbole di equazione: x^2 - y^2 = 16
Elenchiamo i passaggi da effettuare per risolvere questo tipo di esercizio, sul disegno:
- Trovare i fuochi e i vertici;
- Disegnare gli asintoti, che sono sempre le bisettrici;
- Disegnare l’iperbole, partendo dal vertice.
Vedendo l’equazione, capiamo che è equilatera con i fuochi sull’asse x. E con:
a^2 = 16 \implies a = 4 \;\; (non prendiamo il segno meno, perché è già contenuto nelle formule)
Iniziamo col primo punto, troviamo i fuochi. Usiamo quindi le formule:
F_1 = (-\sqrt{2}a ,0), \; F_2 = (\sqrt{2}a,0)
F_1 = (-\sqrt{2}4 ,0), \; F_2 = (\sqrt{2}4,0)
Poi è il turno dei vertici:
V_1 = (-a ,0), \; V_2 = (a,0)
V_1 = (-4 ,0), \; V_2 = (4,0)
Segniamo questi punti sul piano cartesiano, segnandoci anche gli asintoti, che sono sempre le bisettrici.
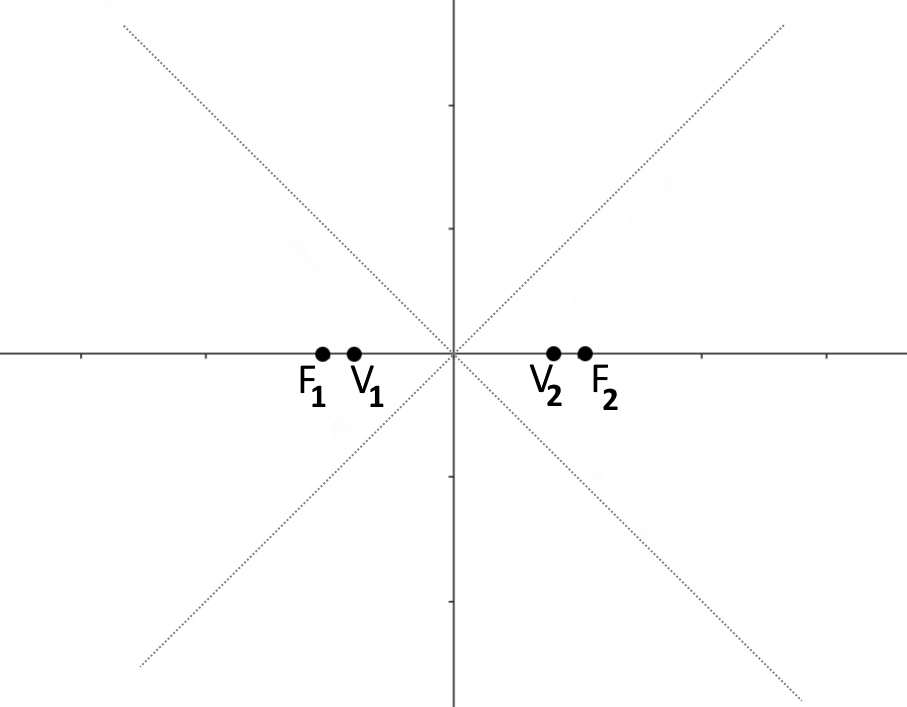
A questo punto non ci rimane altro che mettere penna sul vertice ed iniziare ad andare verso gli asintoti, non facendoli toccare mai. Verrà qualcosa di questo tipo.
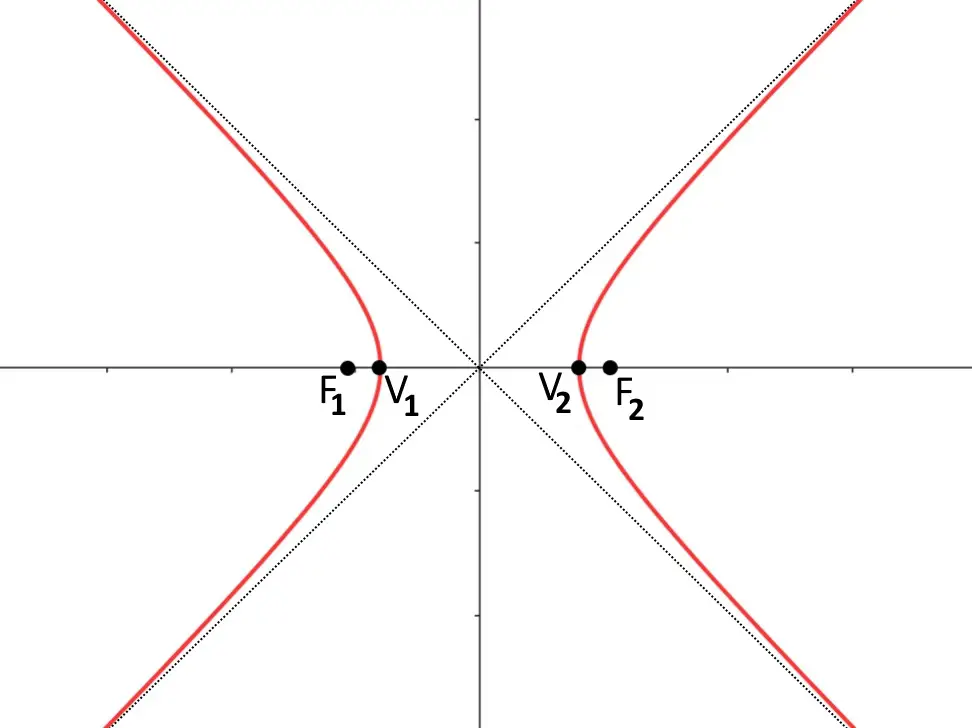
Ecco fatto! Tutto qui! Trovate un altro esercizio svolto cliccando qui.
Questa pagina è conclusa, speriamo vi sia stato chiaro il tutto. Trovate comunque altri centinaia di argomenti ed esercizi svolti di Matematica, Geometria Analitica e anche Geometria!
Continuate a sostenere il nostro sito! A presto!
iperbole
iperbole