Funzione crescente e decrescente:
definizione ed esempi
Funzione crescente e decrescente: definizione ed esempi. In questa pagina vedremo cosa significa e a cosa serve sapere che una funzione può essere crescente o decrescente. Vedremo la definizione, tantissimi esempi, e diverse applicazioni. Tutto spiegato con calma, passo dopo passo. Iniziamo subito!
Indice
- Funzione crescente: definizione
- Funzione crescente in senso stretto
- Funzione decrescente: definizione
- Funzione decrescente in senso stretto
- Esempi
Iniziamo subito, con il dare la definizione di funzione crescente, e vedere alcuni esempi.
Funzione crescente: definizione
Consideriamo una funzione f(x) definita in un dominio D. Ad esempio, la seguente.
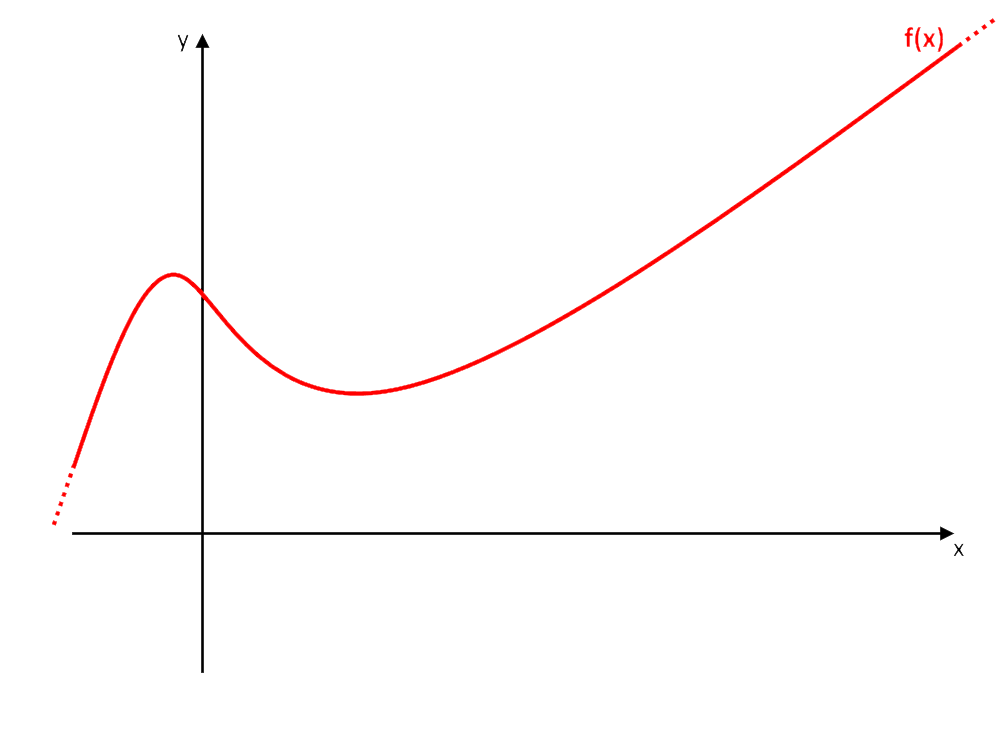
Consideriamo l’intervallo I, sottoinsieme di D. Cioè un intervallo di dominio più piccolo di D.
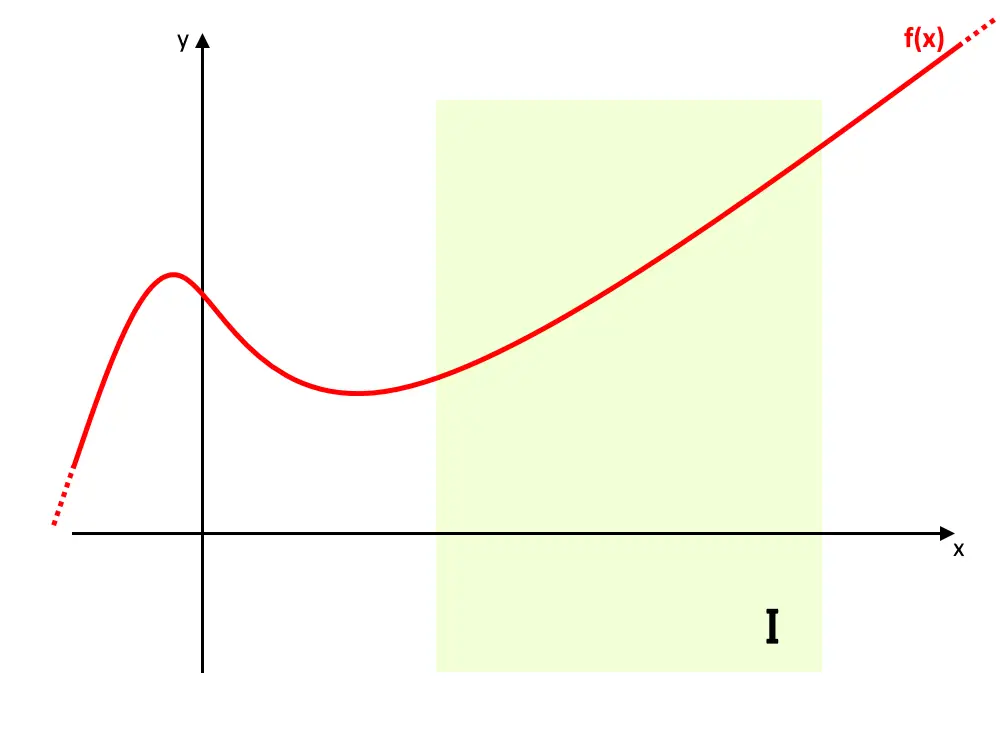
Diciamo che la funzione f(x) è crescente in I se:

Ciò cosa significa in parole povere? Significa che in quel preciso intervallo evidenziato I, la funzione cresce, ossia tende ad andare verso l’alto, sale. Nella definizione c’è scritto f(x_2) \ge f(x_1) , ossia presi due qualsiasi punti x_1 e x_2 il valore della funzione f(x_2) è più grande o uguale di f(x_1) .
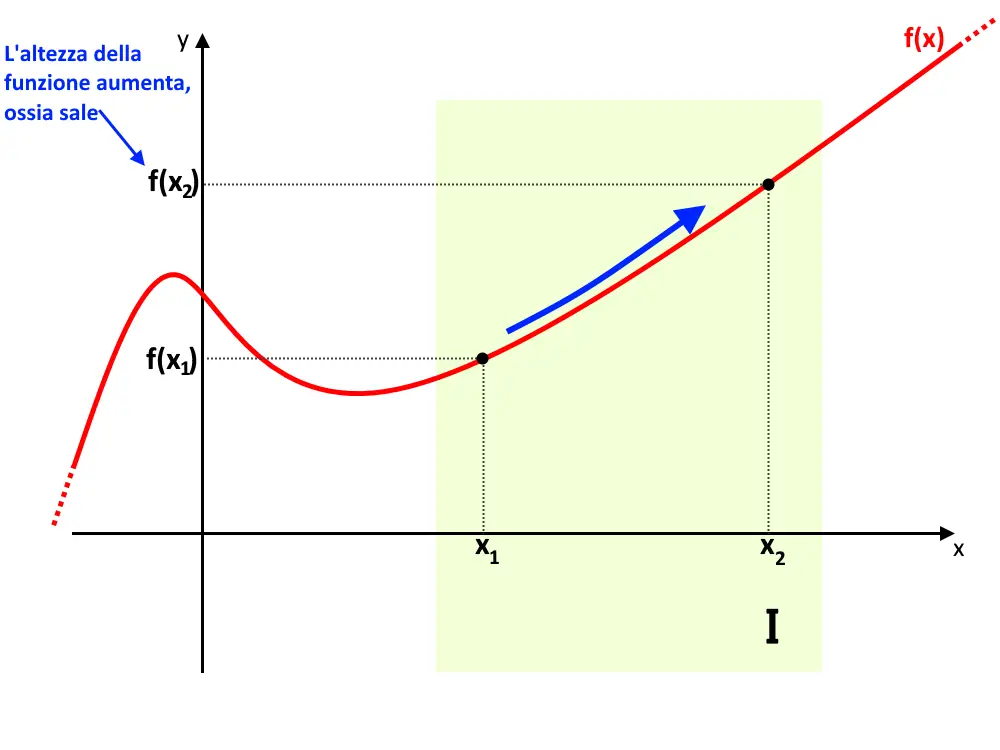
Notate che c’è un maggiore o uguale nella definizione: questo significa che è crescente anche una certa funzione f(x) che tende ad andare verso l’alto oppure a rimanere costante!
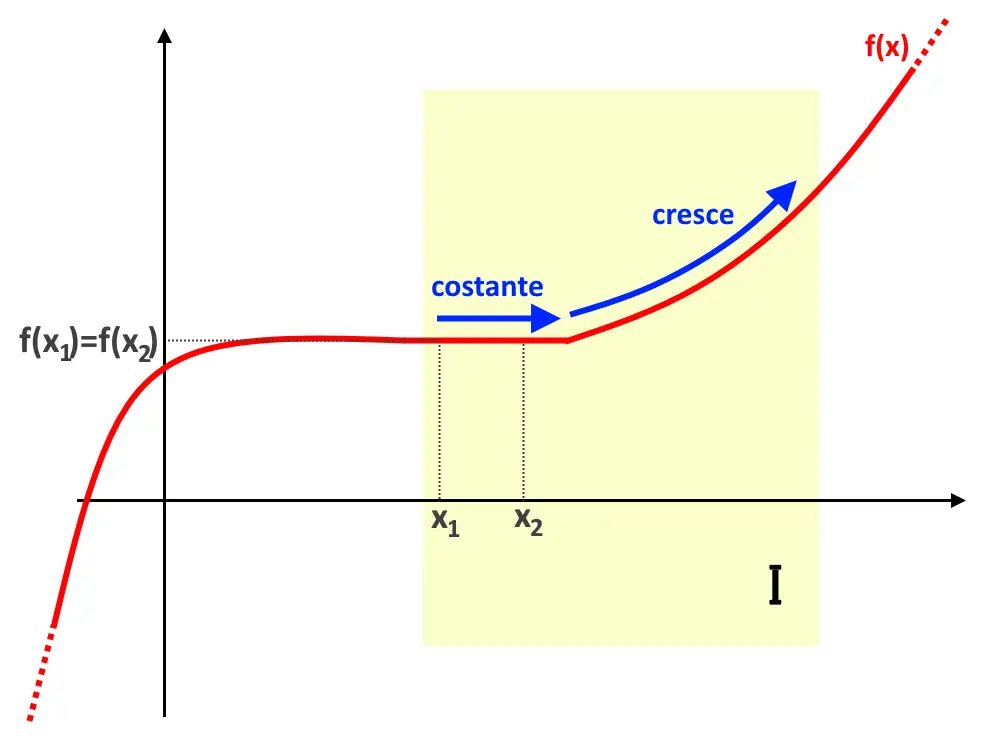
Adesso che abbiamo capito cosa significa che una funzione è crescente, vediamo cosa significa “crescente in senso stretto”.
Funzione crescente in senso stretto
Consideriamo una funzione f(x) definita in un certo dominio D. Consideriamo sempre un sottoinsieme I, come prima.
Una funzione si dice crescente in senso stretto (o monotòna crescente) se:

Cosa è cambiato rispetto a prima? E’ cambiato solamente il segno > piuttosto che il \ge . Cosa vuol dire questo? Vuol dire che ora la funzione cresce sempre, va sempre verso l’alto, quindi non rimane mai costante!
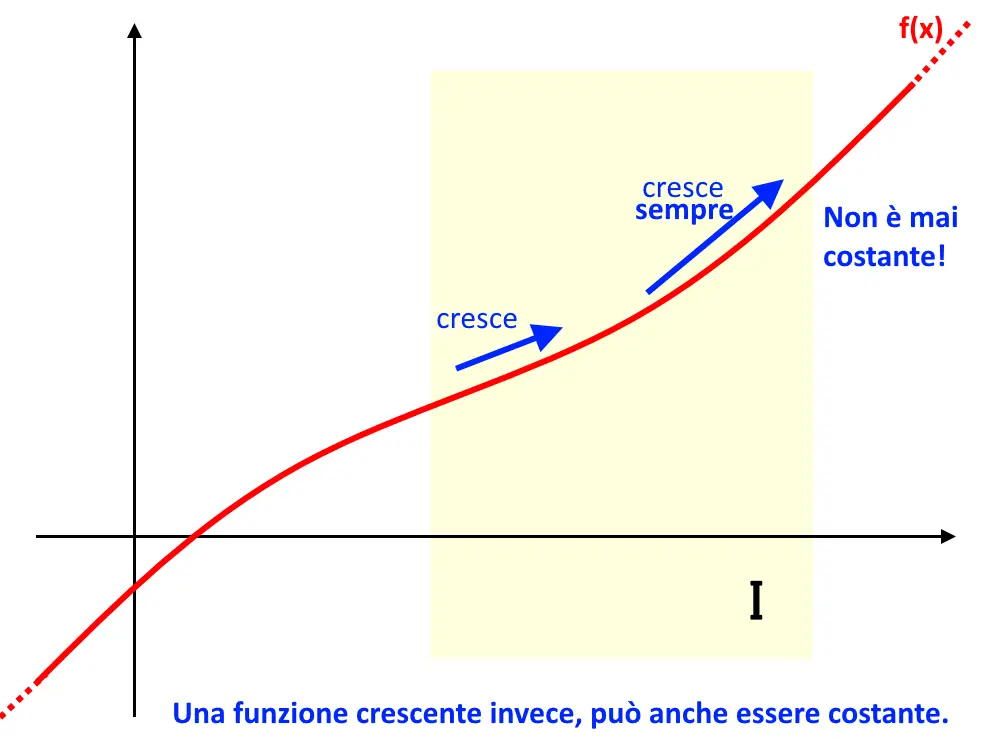
Questa è un affermazione più forte rispetto a prima. L’unica differenza è appunto questa: ora la funzione non può essere costante.
Adesso che abbiamo capito le due definizioni, e cosa significano, vediamo l’altra controparte.
Funzione decrescente: definizione
I concetti che vedremo sono esattamente gli stessi, ma all’inverso. Consideriamo una funzione f(x) definita in un certo dominio D. Consideriamo un sottoinsieme I, di D.
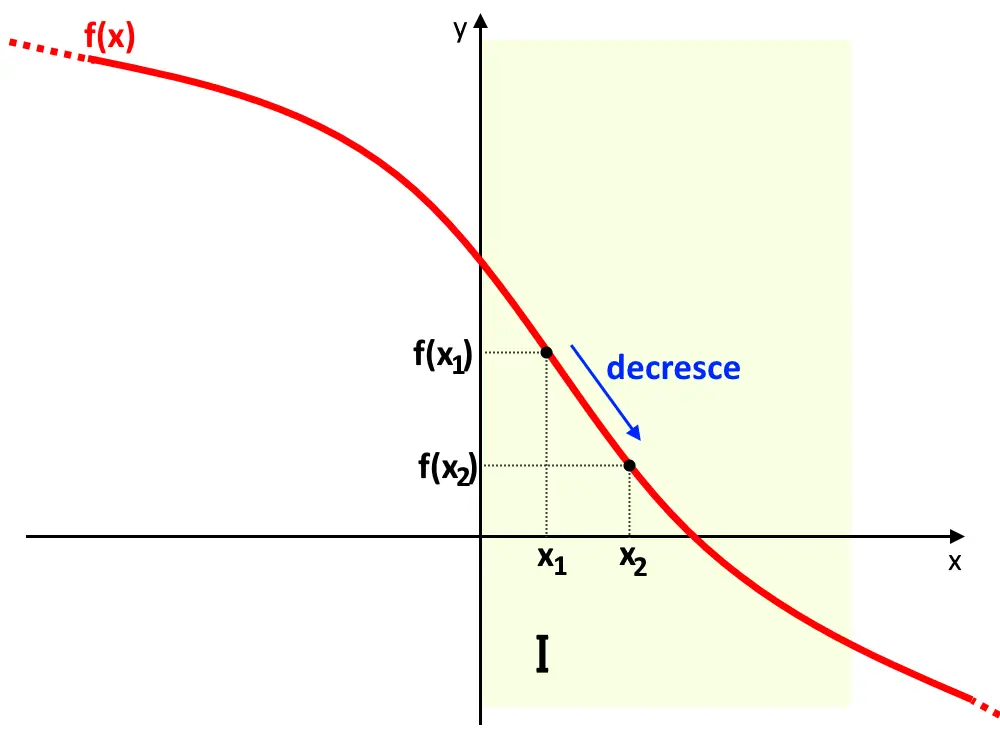
Tale f(x) si dirà decrescente in I (bisogna sempre specificare in quale intervallo) se:

Cosa significa? Proprio come prima, anche qui c’è la presenza del \le e quindi stiamo dicendo che la funzione tende sempre a scendere, ma può anche essere costante.
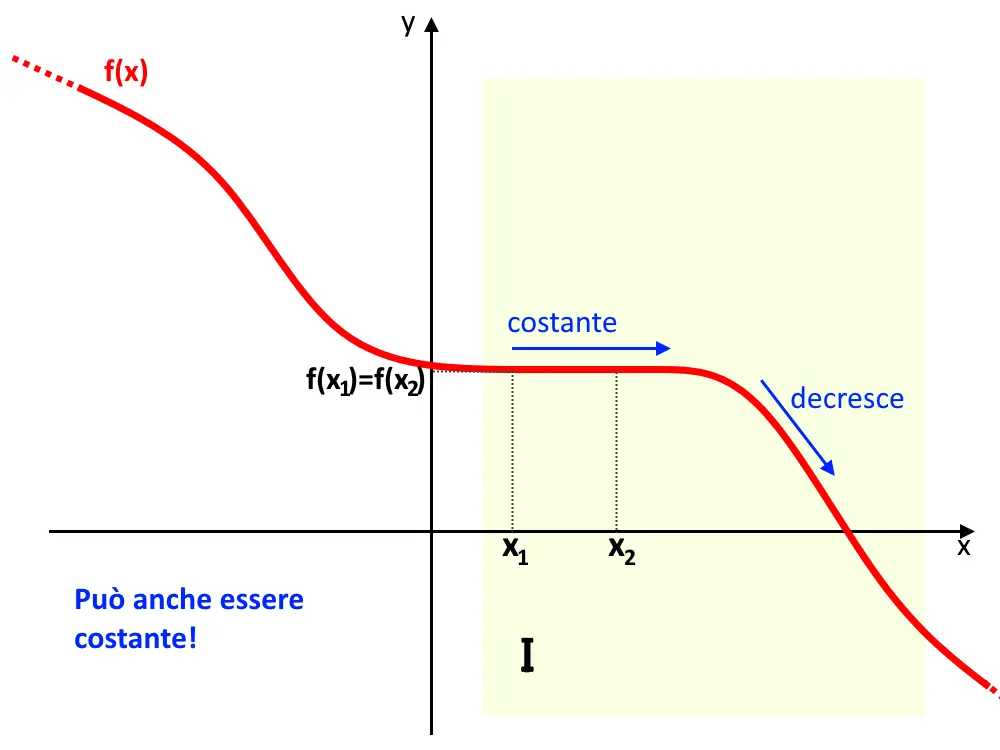
La definizione è praticamente uguale, vi basta semplicemente invertire il segno, tutto qui.
Funzione decrescente in senso stretto
Anche qui andiamo a fare l’analogo di prima. Consideriamo sempre una funzione f(x) definita in D. Sia sempre un sottointervallo ( o sottoinsieme, è uguale) I, di D. La f(x) si dirà monotòna decrescente, o in senso stretto se:

Differenza? L’unica cosa che cambia è che se n’è andato il segno uguale, adesso c’è solamente < ! Questo significa che non vogliamo più che la f(x) sia in qualche intervallo costante. Stiamo dicendo, con questa definizione, che la funzione deve sempre andare verso giù, sempre!
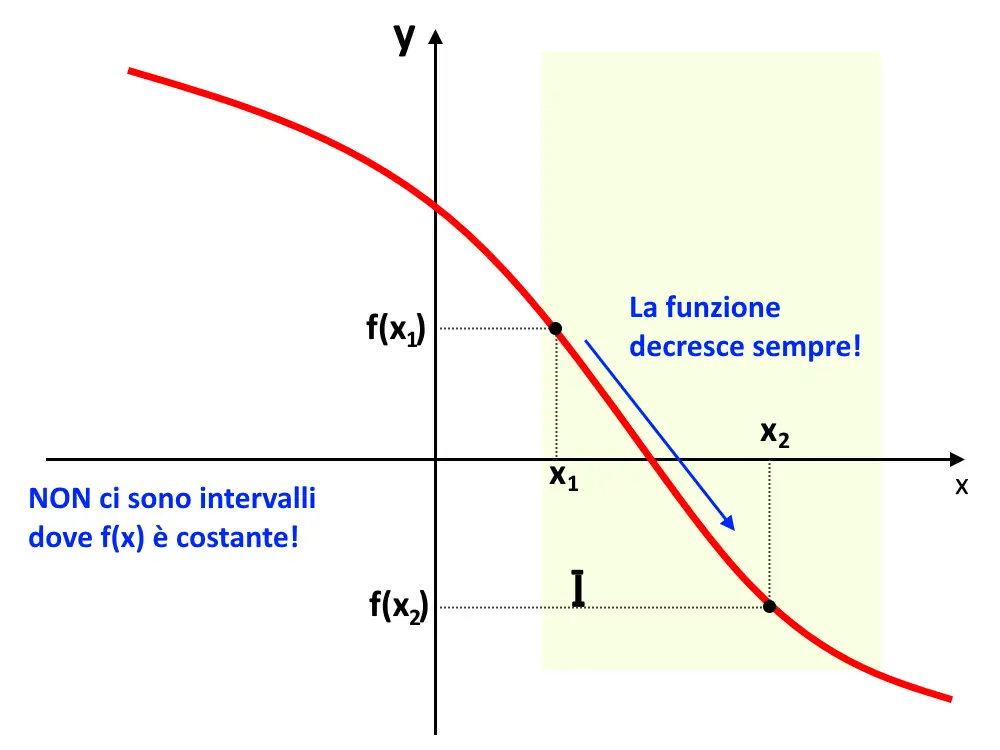
Vediamo degli esempi per capire meglio i concetti che abbiamo visto insieme!
Esempi di funzioni crescenti e decrescenti
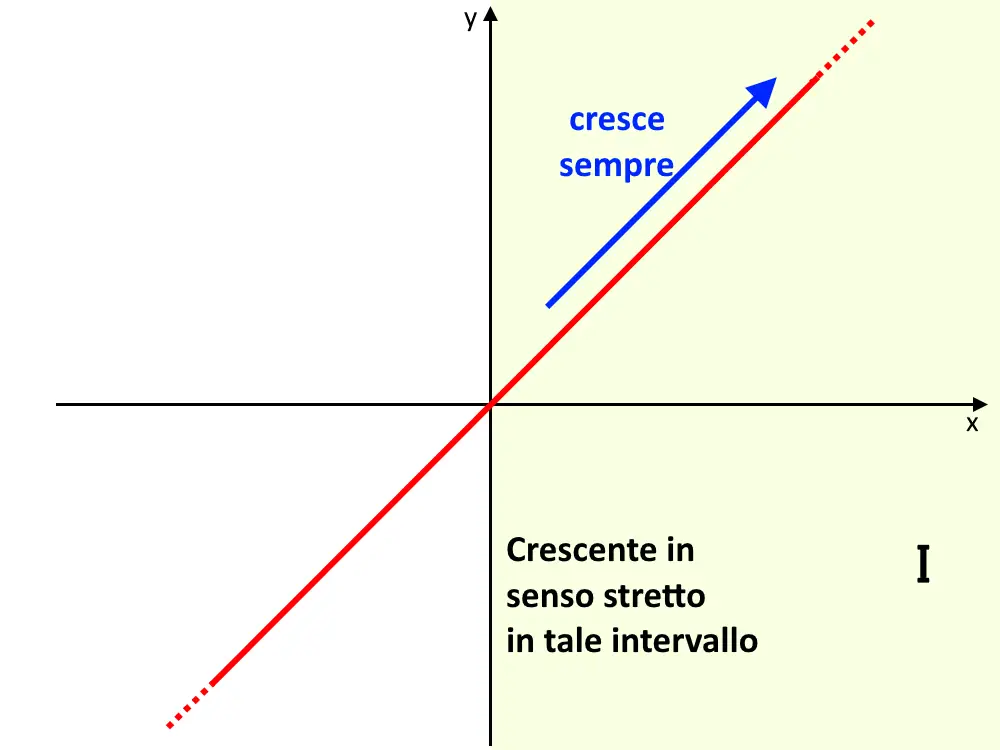
Consideriamo la seguente funzione f(x) = x . Consideriamo ad esempio l’intervallo I, cioè la parte destra del dominio D. Questa è sicuramente crescente in senso stretto, perché oltre a salire, non è mai costante. Ossia sale sempre in tutto I. Chiaramente lo è anche in tutto D.
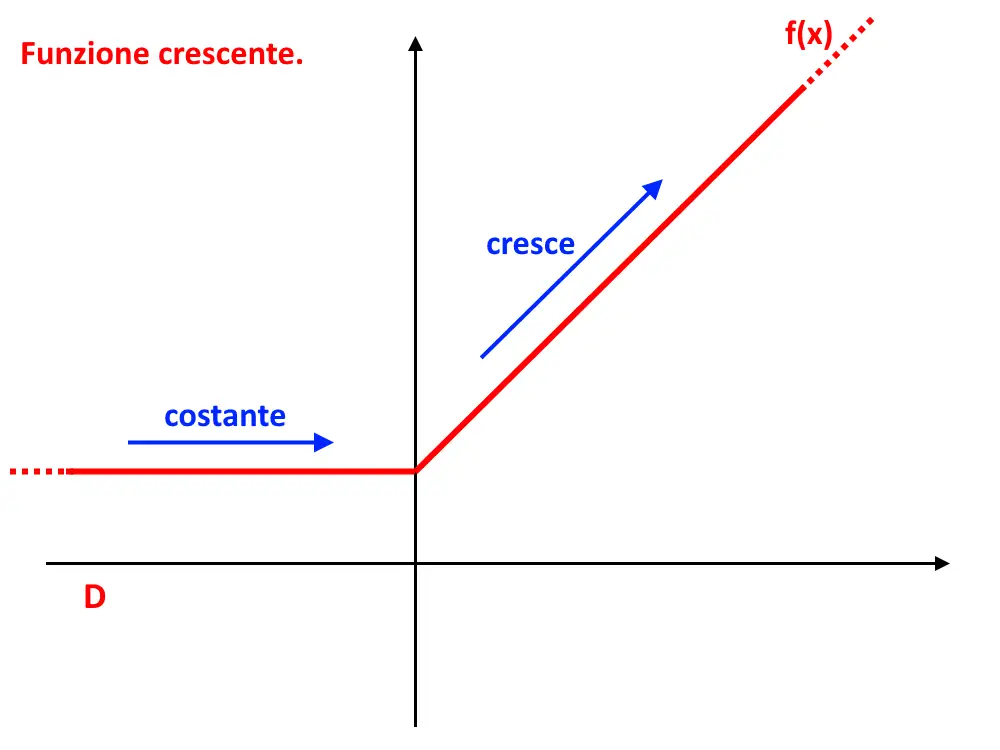
Consideriamo la funzione seguente f(x) = \begin{cases} 1 \;\;\; se \;\;\; x<0 \\ x+1 \;\;\; se \;\;\; x \ge 0 \end{cases} . Consideriamo tutto l’intervallo D, la funzione com’è? All’inizio essa è costante, e poi sale: di conseguenza si dice che è solamente crescente.
Si possono anche considerare più intervalli come nel prossimo esempio. Consideriamo infatti una funzione f(x) definita in D, tutto l’asse x sarebbe. Consideriamo due sottoinsiemi I e I’. Come è la funzione in questi due sottoinsiemi?
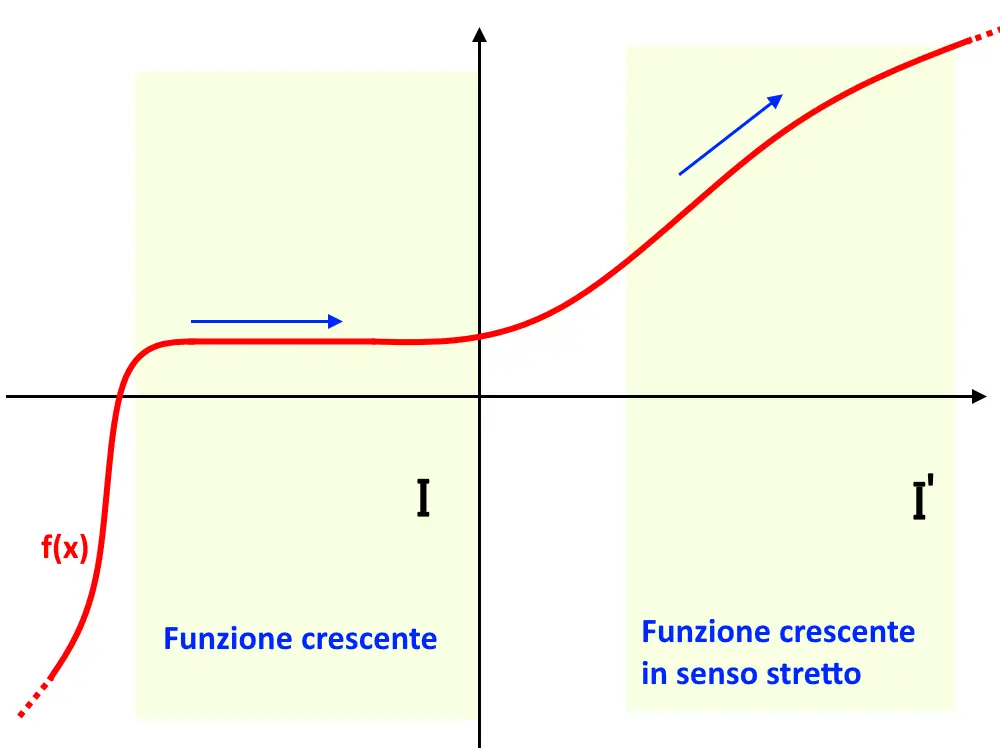
Nel primo sottoinsieme I, la f(x) sale, ma è anche costante, di conseguenza è solamente crescente si dice. Nel secondo sottoinsieme I’ sale sempre, quindi è monotona crescente, o in senso stretto.
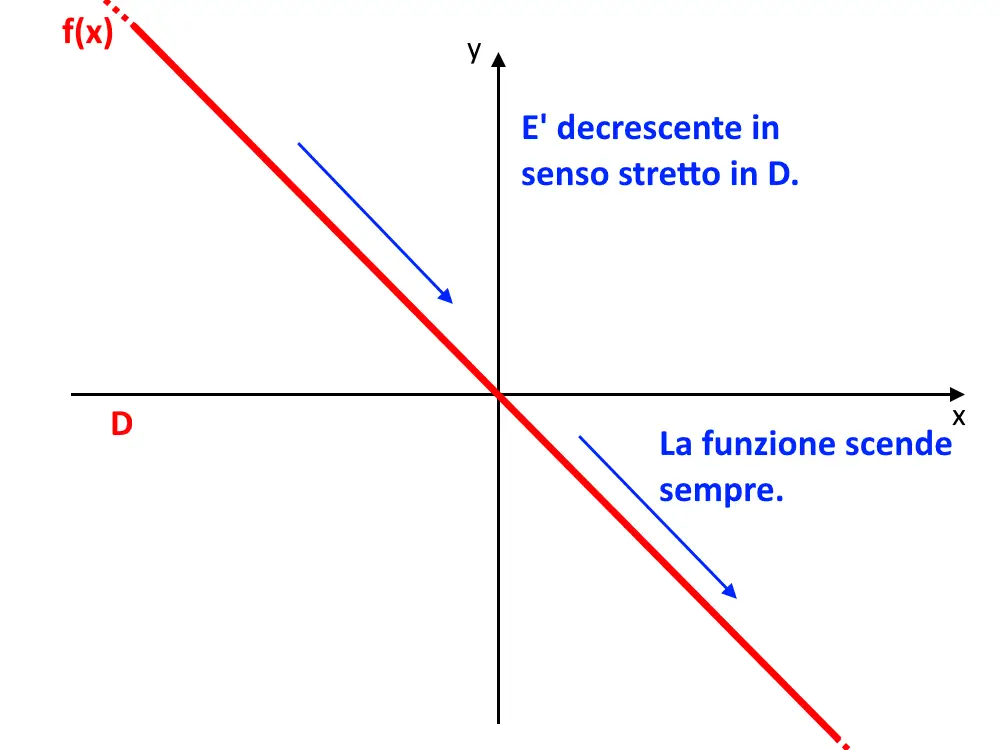
Consideriamo la funzione f(x)=-x. E vogliamo studiare il suo andamento in tutto il suo dominio D. La f(x) è chiaramente monotòna decrescente (o in senso stretto) perché scende sempre e non ha punti in cui è costante.
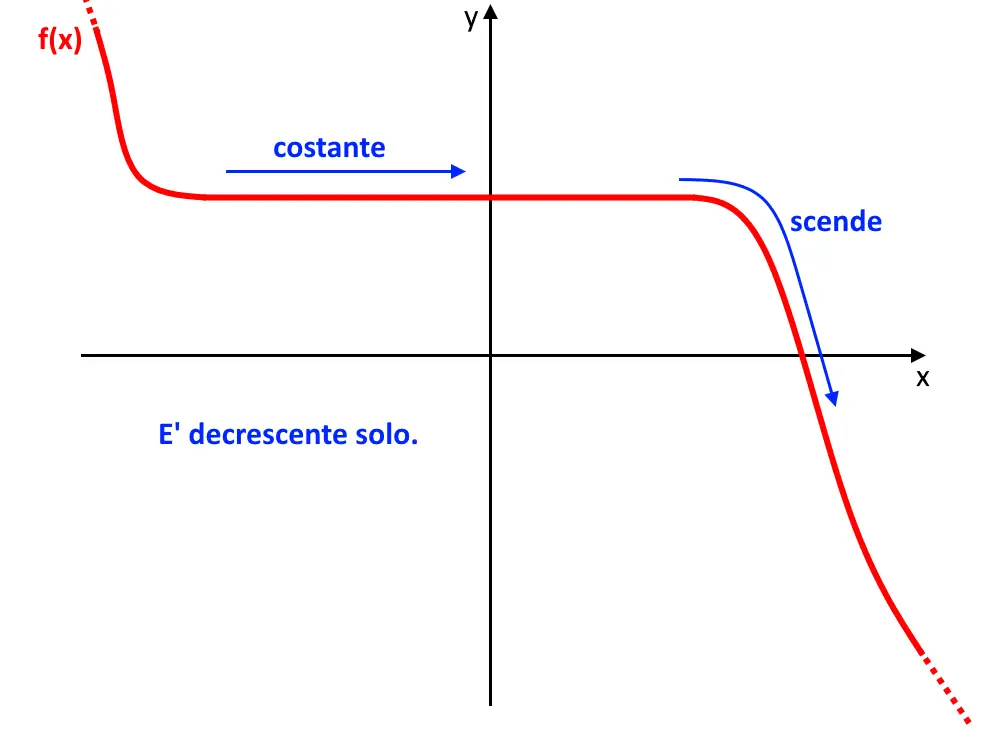
Invece, la funzione seguente f(x), sempre in tutto D, è chiaramente solo decrescente e basta: in alcuni intervalli rimane costante.
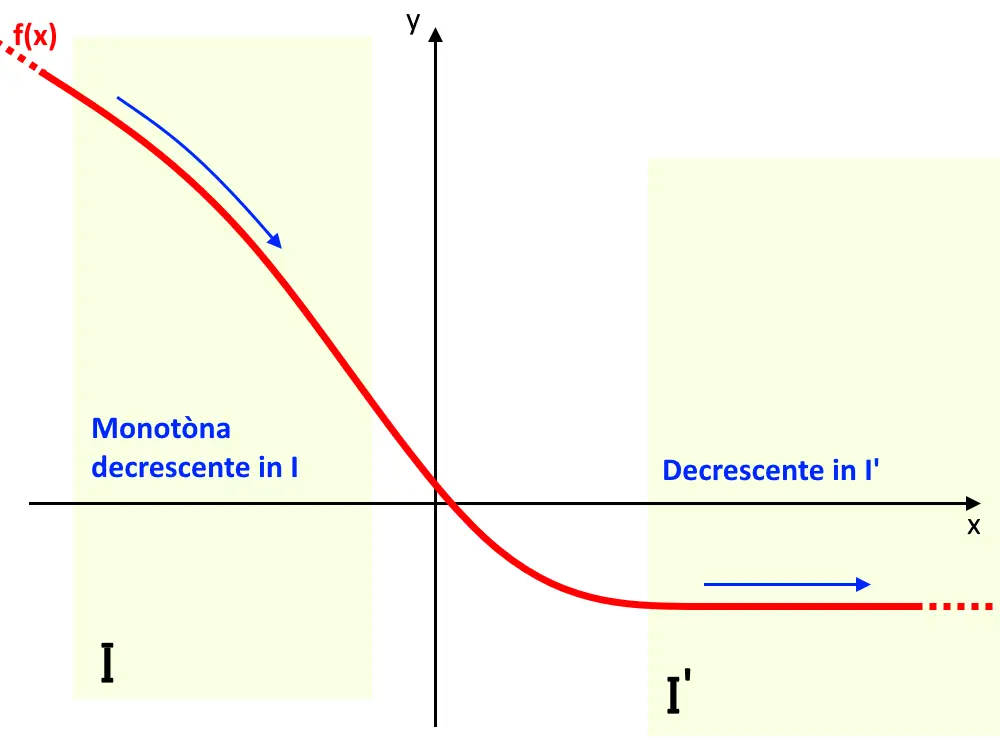
Infine, se consideriamo la seguente funzione f(x) nei due sottointervalli I e I’. Notiamo che in uno la funzione è decrescente in senso stretto, nell’altro solo decrescente perché poi rimane costante ad un certo punto!
La pagina di teoria è terminata. Trovate altri centinaia di argomenti ed esercizi svolti sia di matematica, che di geometria analitica e geometria!
Supportate il sito!
Per approfondire comunque:
https://it.wikipedia.org/wiki/Funzione_monotona
suriettiva
inversa