Sistemi di disequazioni: 15 ESERCIZI SVOLTI
Sistemi di disequazioni: 15 ESERCIZI SVOLTI! Sistemi di disequazioni significa considerare più disequazioni insieme ed unire le soluzioni. In questa pagina vedremo come si fanno, con ben 15 esercizi in ordine di difficoltà. Mostreremo consigli ed altro. E’ assolutamente necessario che vi ripetiate un attimino gli svolgimenti generali di come si risolve una disequazione, che sta alla base dei sistemi poi.
Indice
Vediamo subito come si risolve un sistema di disequazioni, in linea generale. Seguiremo infatti questo procedimento che mostriamo di seguito.
Come si risolve un sistema di disequazioni
Sfruttando questa linea generale, iniziamo a vedere degli esercizi svolti sui sistemi di disequazioni! Se ne avete la possibilità cercate di farli tutti, ognuno dirà qualcosa di diverso. Mostreremo il caso di soluzione “impossibile” o di avere una singola soluzione ecc.
Sistema di due disequazioni
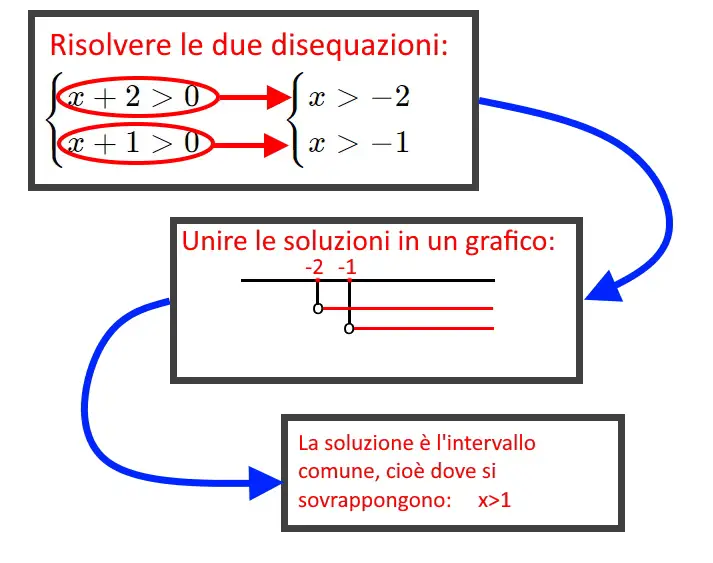
Esercizio 1. \begin{cases} x+4>0 \\ x-3> 0 \end{cases}
Seguendo il procedimento sopra mostrato, quello che dobbiamo fare è inizialmente trattare le due disequazioni in maniera totalmente separata: ossia risolverle una per volta. (Risolvere una disequazione significa arrivare ad un qualcosa del tipo x>-4, cioè x da sola a sinistra e il numero a destra).
Per la prima disequazione portiamo il 4 a secondo membro, per la seconda il -3. Ricordate che quando portate un numero da una parte all’altra si cambia di segno.
\begin{cases} x>-4 \\ x> 3 \end{cases}
Le due disequazioni sono risolte. Solo adesso possiamo unirle, cioè disegniamo un grafico di un sistema. Disegniamo entrambi gli intervalli di soluzioni in due righi diversi, poi essendo un sistema (e non un falso sistema) si prendono gli intervalli in comune. Ricordate di mettere un pallino vuoto (visto che c’è solo > senza uguale) per ricordarvi che non bisogna prendere quei particolari punti nella soluzione finale.
Dobbiamo prendere l’intervallo in comune, ossia le righe che si sovrappongono, e in questo caso notiamo che è:
x>3
La soluzione è questa! L’esercizio è concluso.
Esercizio 2. \begin{cases} 2x-2 \le 3 - (x-10) \\ -5x \le 0 \end{cases}
Svolgiamo le due disequazioni: nella prima leviamo la parentesi, nella seconda disequazione cambiamo innanzitutto di segno.
\begin{cases} 2x-2 \le 3 - x+10 \\ 5x \ge 0 \end{cases}
(Quando si cambia tutto di segno si cambia anche il verso della disequazione)
Adesso, come abbiamo sempre fatto negli esercizi delle disequazioni, portiamo le x a primo membro ed il resto a secondo.
\begin{cases} 2x+x \le 3 +10+2 \\ x \ge 0 \end{cases}
\begin{cases} 3x \le 15 \\ x \ge 0 \end{cases}
Dividendo per 3, abbiamo risolto le due disequazioni:
\begin{cases} x \le 5 \\ x \ge 0 \end{cases}
Anche adesso facciamo un grafico del sistema, come prima. In più ricordiamoci di mettere dei pallini pieni, per poi avere la possibilità di prendere anche x=5 e x=0 all’interno della soluzione.
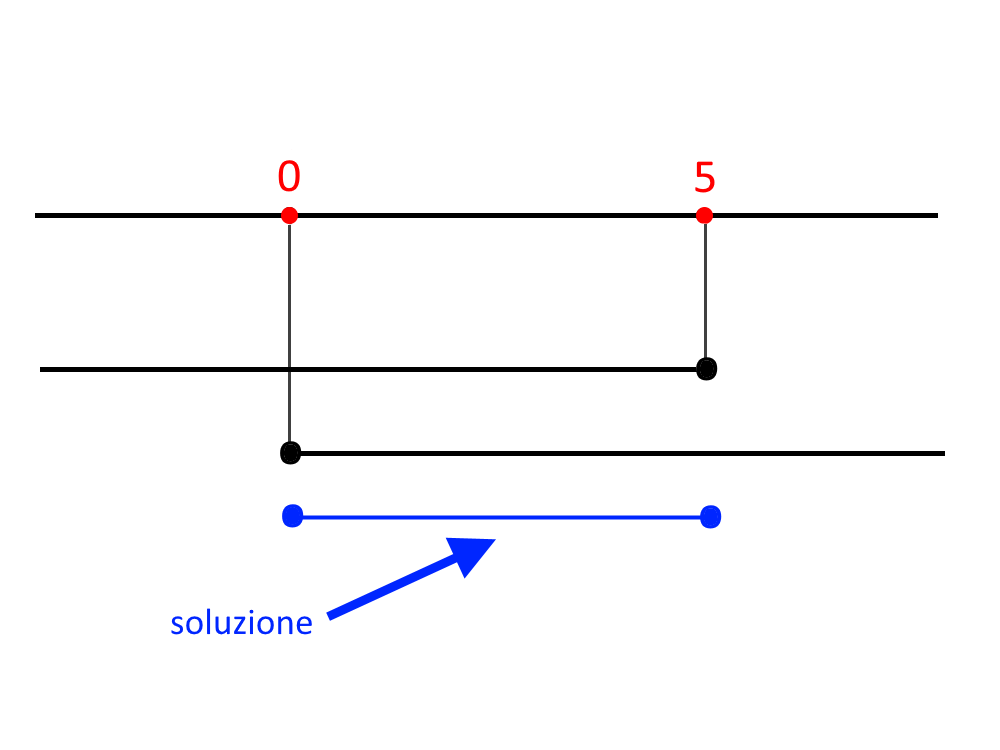
E’ un sistema: prendiamo quindi l’intervallo comune. L’intervallo di soluzione comune, che poi è la soluzione dell’esercizio è:
0 \le x \le 5
Dove, come potete osservare, abbiamo preso anche gli estremi, visto che i due intervalli avevano dei pallini pieni.
Esercizio 3. \begin{cases} 2t+5>5t -2 \\ 3(t+4) -t \le 0 \end{cases}
Qui abbiamo una disequazione nella variabile t: ciò non cambia nulla perché una variabile potete chiamarla x,y o t, non fa nessuna differenza. Lo svolgimento è dunque come sempre. Trattiamo la t come se fosse una classica x. Portiamo le t a sinistra, e poi leviamo la parentesi nella seconda disequazione:
\begin{cases} 2t-5t> -2-5 \\ 3t+12 -t \le 0 \end{cases}
\begin{cases} -3t> -7 \\ 3t -t \le -12 \end{cases}
Sommiamo anche nel secondo, e nel primo dividiamo per 3:
\begin{cases} t< \frac{7}{3} \\ 2t \le -12 \end{cases}
\begin{cases} t< \frac{7}{3} \\ t \le -6 \end{cases}
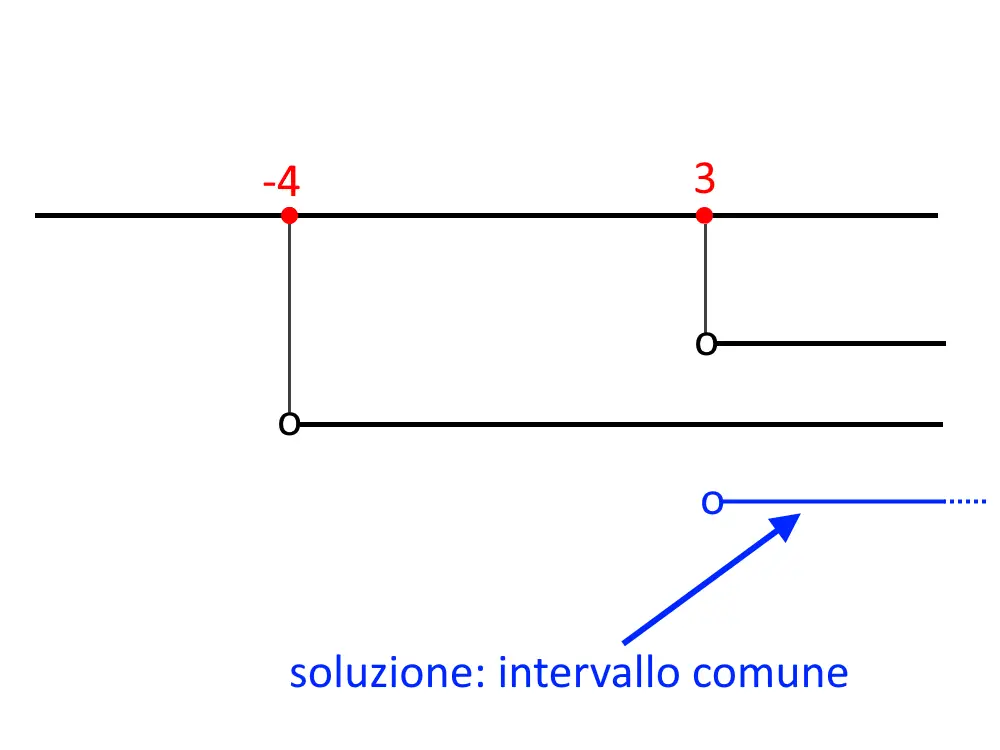
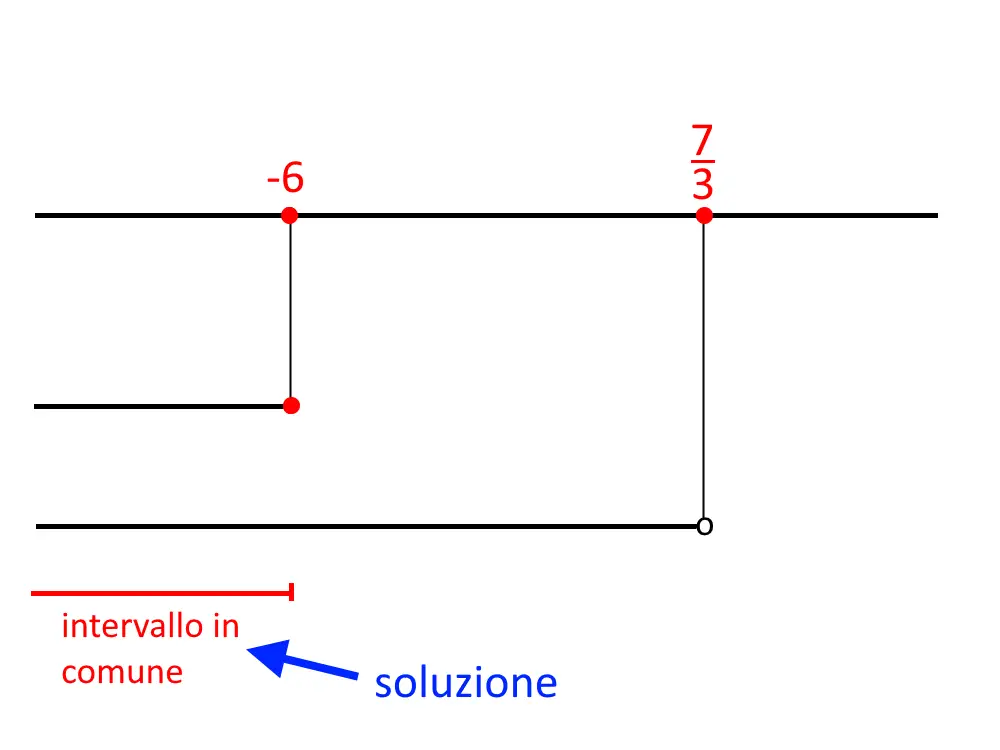
Disegniamo il grafico del sistema, e si prende come soluzione quindi:
t \le -6
Continuiamo con altri sistemi di disequazioni esercizi svolti!
Esercizio 4. \begin{cases} (x-2)^2 +3 \le (x-3)(x+3) \\ x-5> 0 \end{cases}
La prima disequazione del sistema l’avevamo già discussa nella pagine degli esercizi sulle disequazioni: avevamo detto che visto che compaiono dei termini quadratici, essi dovranno andare via in qualche modo, altrimenti non ci troviamo. Questo perché esse devono rimanere disequazioni di primo grado!
Ci servirà per la risoluzione, la formula del quadrato di un binomio.
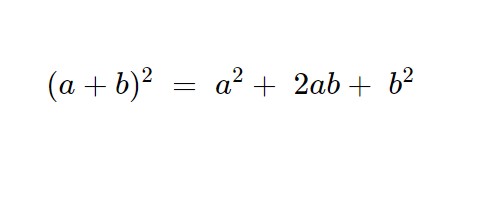
E poi figura a destra anche la differenza di quadrati.
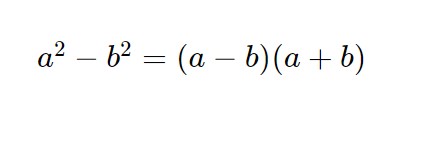
Applicando tali nella prima disequazione otteniamo:
\begin{cases} x^2+4 -4x +3 \le x^2 - 9 \\ x> 5 \end{cases}
E di fatti portando tutte le x a primo membro notiamo che i termini quadratici se ne vanno, è una prova che stiamo andando bene!
\begin{cases} -4x \le -4-3 - 9 \\ x> 5 \end{cases}
\begin{cases} -4x \le -16 \\ x> 5 \end{cases}
E quindi otteniamo:
\begin{cases} x \ge 4 \\ x> 5 \end{cases}
Nel grafico del sistema, la soluzione in comune è l’intervallo:
x>5
Continuiamo con altri sistemi di disequazioni esercizi svolti, ora un po’ più difficili!
Sistemi di disequazioni:
livello medio
Esercizio 5. \begin{cases} (x-2)(3x+1) - 3x^2 < 2(x + \frac{1}{2} ) \\ -1 + 4x (x+1) \le (-2x)^2 \end{cases}
Qui ci sono da svolgere un bel po’ di parentesi, diamoci da fare e ricontrolliamo sempre!
\begin{cases} 3x^2 +x -6x -2 - 3x^2 < 2x + 1 \\ -1 + 4x^2 +4x \le 4x^2 \end{cases}
Portiamo le x a primo membro, e se i termini quadratici non se ne vanno, torniamo indietro e ricontrolliamo. Ma vediamo che se ne vanno!
\begin{cases} 3x^2 +x -6x - 3x^2 -2x < + 1+2 \\ + 4x^2 +4x -4x^2 \le 1 \end{cases}
Sommiamo e le due disequazioni diventano in una forma molto più semplice e compatta, ottimo!
\begin{cases} -7x < 3 \\ +4x \le 1 \end{cases}
\begin{cases} x > - \frac{3}{7} \\ x \le \frac{1}{4} \end{cases}
Qui c’è da stare attenti quando andiamo a disegnare il grafico del sistema, perché nel primo rigo abbiamo una disequazione col pallino vuoto, nel secondo col pallino pieno.
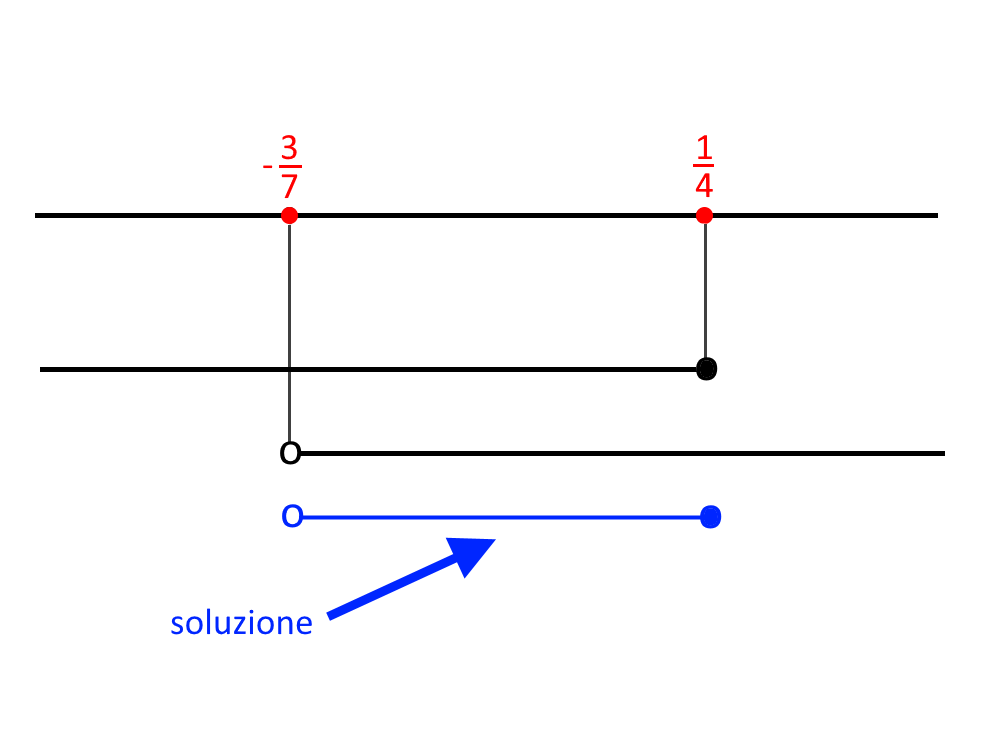
Di conseguenza l’intervallo comune presenta l’estremo sinistro senza l’uguale, e l’estremo destro con l’uguale:
- \frac{3}{7} < x \le \frac{1}{4}
Esercizio 6. \begin{cases} -x > 5 \\ 3x> 12 + x \end{cases}
Esercizio molto importante: vediamo la soluzione “impossibile”! Risolviamo il sistema come sappiamo fare, dopo vedremo qualcosa di particolare.
\begin{cases} x < - 5 \\ 2x> 12 \end{cases}
\begin{cases} x < - 5 \\ x> 6 \end{cases}
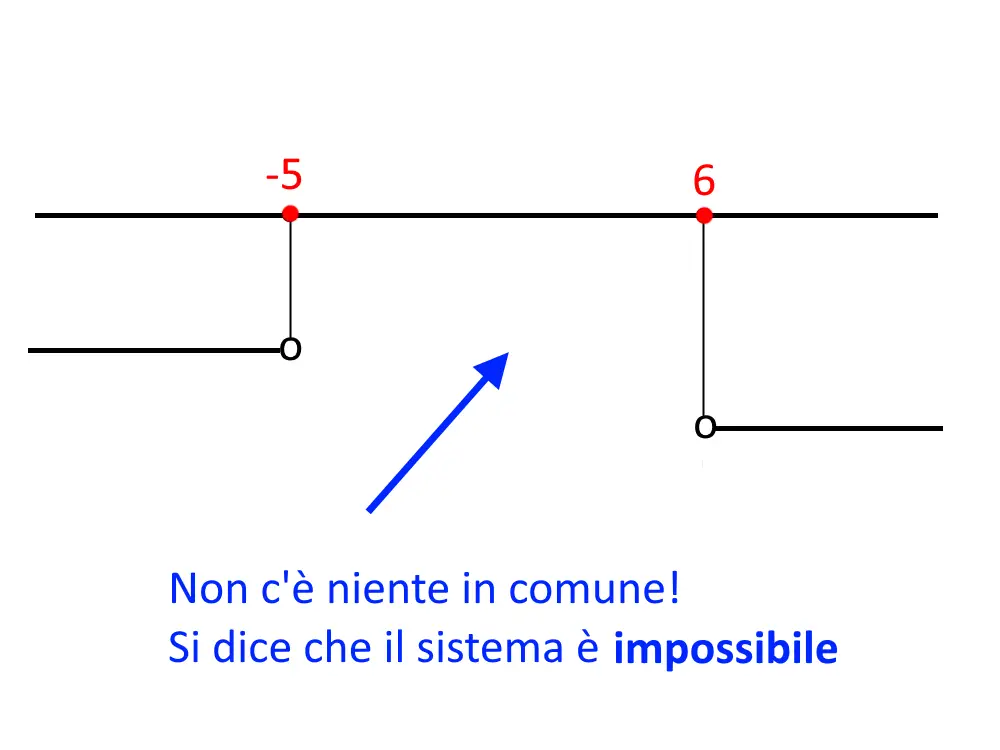
Disegniamo il grafico del sistema, e notiamo che nessuna porzione di intervallo viene sovrapposta, non c’è nulla in comune. Uno va verso destra ed uno verso sinistra. In questi casi, quando non c’è nessuna sovrapposizione, si dice che il sistema non ha soluzione o:
impossibile
Esercizio 7. \begin{cases} x(4x+5 ) - (2x-2)^2 \ge 1 \\ (x-1)(x+1) > (x+2)^2 \end{cases}
Anche qui balza subito all’occhio un quadrato del binomio e la differenza di quadrati, utilizziamo suddette formule.
\begin{cases} 4x^2+5x - (4x^2 + 4 -8x) \ge 1 \\ x^2 - 1 > x^2+4 +4x \end{cases}
Da notare che nel primo quadrato abbiamo tenuto la parentesi: questo perché prima vi si applica il quadrato, e poi il segno meno che moltiplica tutto.
\begin{cases} 4x^2+5x - 4x^2 - 4 +8x \ge 1 \\ x^2 - 1 > x^2+4 +4x \end{cases}
\begin{cases} 4x^2+5x - 4x^2 +8x \ge 1+4 \\ x^2 -x^2 -4x> 4+1 \end{cases}
Sommiamo e ricaviamo che il sistema risulta essere:
\begin{cases} 13x \ge 5 \\ -4x> 5 \end{cases}
Con le due disequazioni svolte:
\begin{cases} x \ge \frac{5}{13} \\ x< - \frac{5}{4} \end{cases}
Il grafico del sistema anche in questo caso presenta nessun intervallo in comune. La soluzione è per cui:
Impossibile
Continuiamo con altri sistemi di disequazioni esercizi svolti!
Esercizio 8. \begin{cases} -x +8 \ge 9 \\ 2x+5 \ge 3 \end{cases}
Esercizio importantissimo: vedremo come fa ad uscire una singola soluzione (tipo x=2) in un sistema di disequazioni.
Iniziamo a svolgere le due disequazioni, che sappiamo fare. Anzi fatelo voi, ci vediamo dopo!
\begin{cases} -x \ge 9-8 \\ 2x \ge 3-5 \end{cases}
\begin{cases} x \le - 1 \\ x \ge - 1 \end{cases}
Nel grafico del sistema accade una cosa particolarissima: i due intervalli non si sovrappongono per esteso, ma hanno un singolo punto in comune.
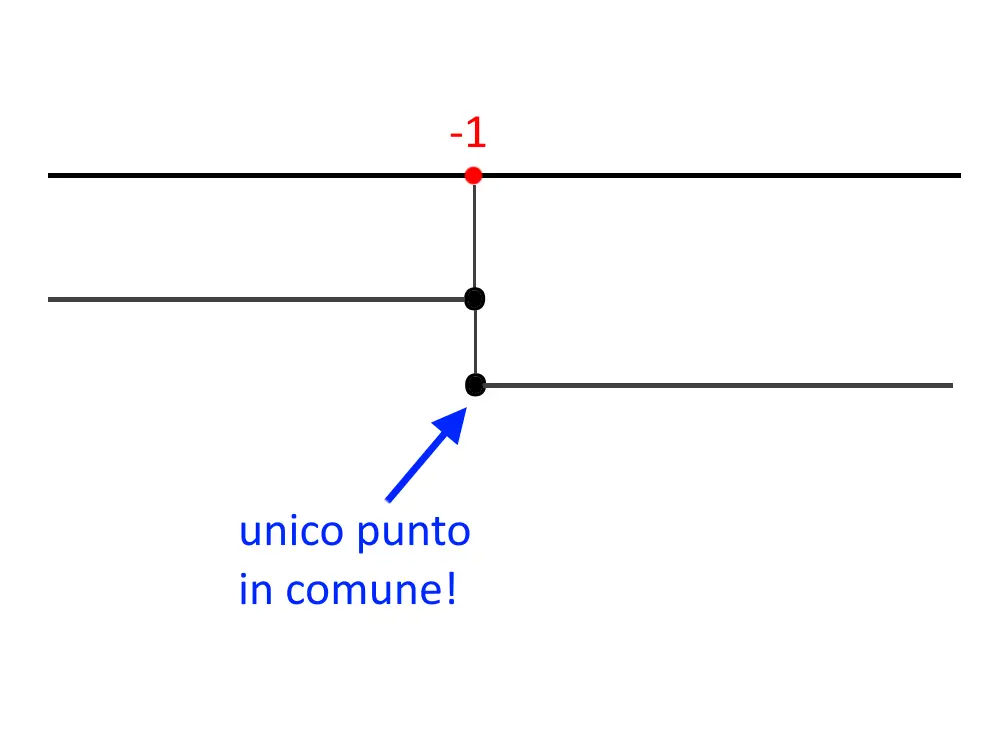
Un singolo punto in comune, anche se un punto solo, è sempre qualcosa in comune che hanno! La soluzione è per cui solamente:
x=-1
ATTENZIONE: questo accade perché le due disequazioni hanno come segno \le , \ge , di conseguenza x=-1 è un punto che possiamo prendere in considerazione. Ma se avessero avuto < e > non ci sarebbe stata soluzione, come vediamo nel prossimo esercizio.
Esercizio 9. \begin{cases} 2x > 4 \\ x < 2 \end{cases}
Questo è il caso opposto all’esercizio di prima, vi faremo vedere cosa accade quando abbiamo lo stesso esercizio di prima, ma con pallini vuoti. Il sistema risolto risulta essere:
\begin{cases} x > 2 \\ x < 2 \end{cases}
Nel grafico del sistema, abbiamo il caso analogo a prima. Solamente che ora i pallini sono vuoti, di conseguenza x=2 NON va preso in considerazione. I due intervalli allora non hanno proprio nessun punto in comune, neanche x=2!
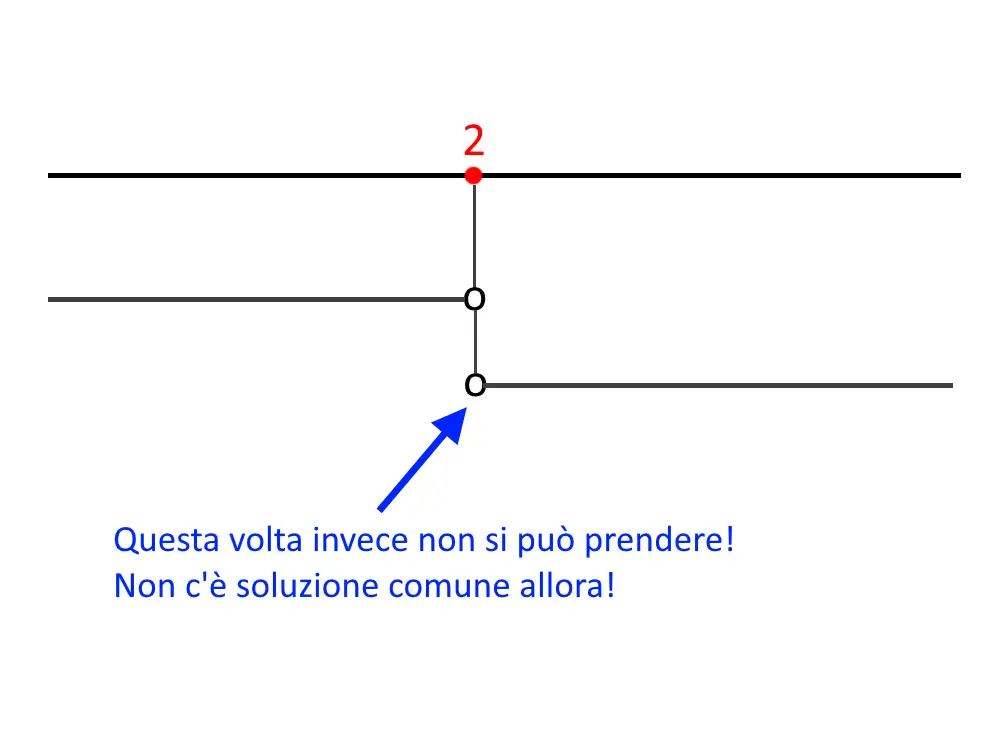
Il sistema non ha soluzione o si dice che è “impossibile”.
Esercizio 10. \begin{cases} 2b^2 - 2(b+2)^2 + 8(b-4) < -1 \\ 2b - \frac{4}{3} (b+3 ) - \frac{2}{3}b <0 \end{cases}
Esercizio importante: in questo vedremo come soluzione “per ogni x”. Iniziamo a svolgere le parentesi delle due disequazioni nel sistema, cosa che sapete fare. La differenza starà alla fine!
\begin{cases} 2b^2 - 2(b^2 + 4 +4b) + 8b-32 < -1 \\ 2b - \frac{4}{3}b - 4 - \frac{2}{3}b <0 \end{cases}
Riordiniamo un po’ tutto questo casino, levando quella parentesi tonda e portando le b a primo membro!
\begin{cases} 2b^2 - 2b^2 - 8 -8b + 8b-32 < -1 \\ 2b - \frac{4}{3}b - 4 - \frac{2}{3}b <0 \end{cases}
\begin{cases} 0b < 39 \\ 2b - \frac{4}{3}b - \frac{2}{3}b < 4 \end{cases}
Facciamo anche il minimo comune multiplo fra le b nella seconda disequazione:
\begin{cases} 0b < 39 \\ \frac{6b-4b-2b}{3} < 4 \end{cases}
\begin{cases} 0b < 39 \\ 0b < 4 \end{cases}
Questi due tipi di disequazioni li abbiamo visti negli esercizi sulle disequazioni. Abbiamo detto che quando viene fuori questo bisogna porsi una domanda.
Per 0b<39 ci chiediamo: 0 è più piccolo di 39? Sì, quindi essa ha come soluzione \forall b
Per 0b<4 ci chiediamo: 0 è più piccolo di 4? Sì, quindi anch’essa ha come soluzione \forall b
Il sistema si riscrive alla fine nel modo seguente:
\begin{cases} \forall b \\ \forall b \end{cases}
La soluzione \forall b in un grafico di un sistema, si disegna con una linea retta. Quindi noi abbiamo due linee rette!
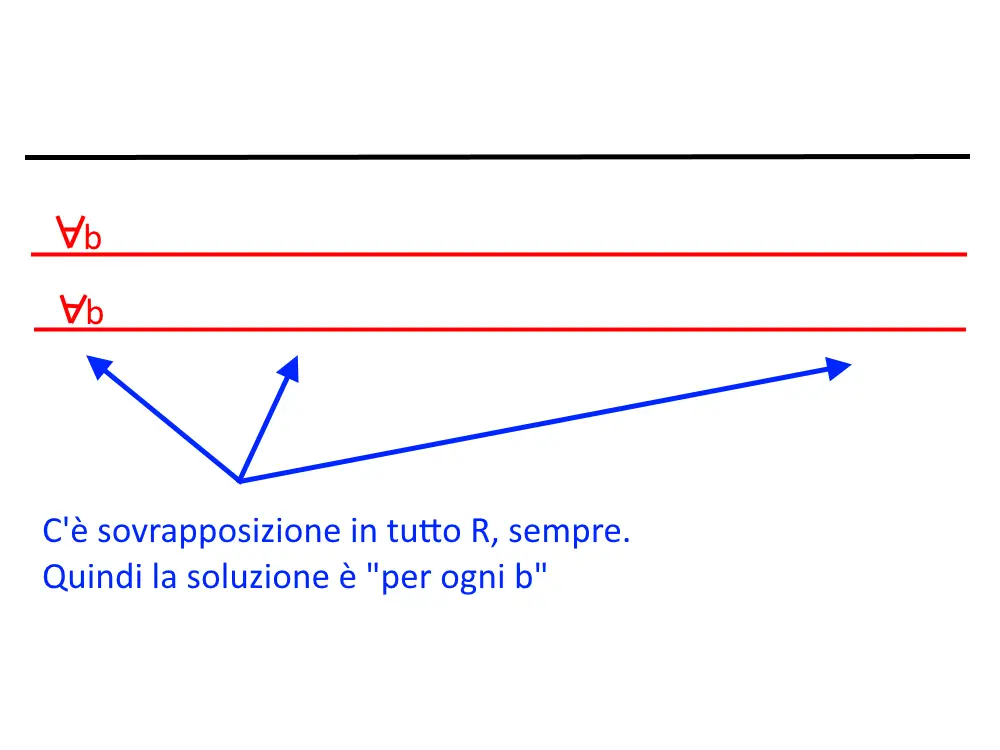
La soluzione in comune è chiaramente tutto proprio! Quindi la soluzione finale sarà:
\forall b
Esercizio 11. \begin{cases} x(2x+1) - 2x^2 -x > 4 \\ (x-2)^4 > 2x -2 \end{cases}
Qui vi sveliamo un utilissimo trucchetto: la seconda disequazione è davvero difficile. Partiamo dalla prima, senza toccare la seconda: questo perché può accadere una cosa particolare.
\begin{cases} 2x^2+x - 2x^2 -x > 4 \\ (x-2)^4 > 2x -2 \end{cases}
Ripetiamo che non tocchiamo la seconda.
\begin{cases} 0x > 4 \\ (x-2)^4 > 2x -2 \end{cases}
A questo punto per la prima disequazione ci chiediamo: 0 è più grande di 4? No, quindi essa ha come soluzione “nessuna x” o “impossibile”.
\begin{cases} \nexists x \\ (x-2)^4 > 2x -2 \end{cases}
Questo significa che non c’è bisogno di svolgere la seconda disequazione, ora vi spieghiamo il perché. In un sistema si prendono, abbiamo detto, soluzioni in comune. Nel grafico del sistema un \nexists x si disegna con una linea tratteggiata. Di conseguenza qualsiasi sia la soluzione della seconda disequazione, essa sicuramente non avrà nulla in comune con la prima, perché essa non ha proprio soluzioni. Quindi senza fare ulteriori calcoli diciamo che il sistema è impossibile.
Adesso continuiamo con altri esercizi svolti su sistemi di tre disequazioni questa volta!
Sistemi di tre disequazioni
Esercizio 12. \begin{cases} 1-2x \le 3 \\ 5x-1 <1 \\ -x+6 > 6 \end{cases}
Il discorso dello svolgimento di un sistema a tre disequazioni è l’estensione di quello a due disequazioni: l’unica cosa che cambia è la risoluzione di una disequazione in più, e il grafico del sistema che ora è a tre righe. Sviluppiamo le tre disequazioni sempre separatamente:
\begin{cases} -2x \le 3-1 \\ 5x <1+1 \\ -x > 6-6 \end{cases}
\begin{cases} -2x \le 2 \\ 5x <2 \\ -x > 0 \end{cases}
Equivalente a:
\begin{cases} x \ge -1 \\ x < \frac{2}{5} \\ x < 0 \end{cases}
Ora avviene la vera differenza: disegniamo un grafico del sistema a tre righi. Essendo un sistema, la soluzione sarà l’intervallo comune a tutti e tre i righi! Quindi ora dobbiamo trovare intervalli comuni alle tre disequazioni contemporaneamente. Per ogni disequazione controllate sempre quale pallino mettere (se pieno o vuoto).
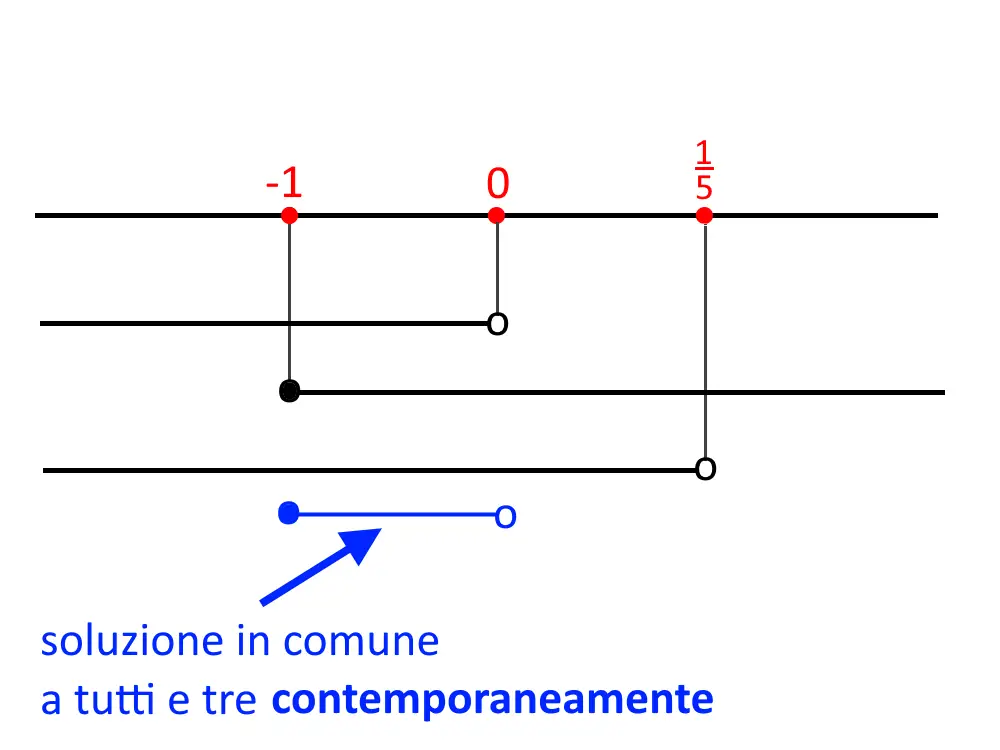
L’intervallo comune a tutti e tre è:
-1 \le x < 0
Esercizio 13. \begin{cases} -2(x+3) < 1-9x \\ 5x \ge 1 \\ \frac{2}{3} - x + \frac{2x-4}{5} > \frac{x-1}{2} \end{cases}
Una cosa alla volta: la prima disequazione leviamo la parentesi, la seconda è semplice, la terza contiene delle frazioni per cui facciamo un minimo comune multiplo a primo membro (così otteniamo solo due frazioni).
\begin{cases} -2x -6 < 1-9x \\ x \ge \frac{1}{5} \\ \frac{10 -15x +3(2x-4) }{15} > \frac{x-1}{2} \end{cases}
Svolgendo i calcoli:
\begin{cases} -2x+9x < 1+6 \\ x \ge \frac{1}{5} \\ \frac{-9x-2 }{15} > \frac{x-1}{2} \end{cases}
A questo punto possiamo sommare nella prima disequazione, nella terza invece moltiplichiamo tutto per 30 (massimo comune divisore) così eliminamo entrambi i denominatori e ci siamo levati da mezzo queste fastidiose frazioni!
\begin{cases} 7x < 7 \\ x \ge \frac{1}{5} \\ 2(-9x-2) > 15(x-1) \end{cases}
E ci troviamo il seguente sistema finale:
\begin{cases} x < 1 \\ x \ge \frac{1}{5} \\ x < \frac{1}{3} \end{cases}
Disegniamo il grafico (o schema dei segni) di tale sistema. La soluzione è l’intervallo comune:
\frac{1}{5} \le x < \frac{1}{3}
Continuiamo con altri sistemi di disequazioni esercizi svolti, ora un po’ più difficili!
Esercizio 14. \begin{cases} 5x+1 \le -2(x-11) \\ 4-4x > 11 \\ x-3 > -(1-x) \end{cases}
Questa provatela voi a fare! Poi rivenite a controllare!
\begin{cases} 5x+1 \le -2x+22 \\ -4x > 11-4 \\ x > -1+x+3 \end{cases}
\begin{cases} 7x \le 21 \\ -4x > 7 \\ 0x > 2 \end{cases}
Le prime due disequazioni non serve più toccarle, perché notiamo che la terza disequazione è 0x>2.
Domanda: 0 è più grande di 2? No, quindi tale disequazione risulta essere impossibile. E, come detto qualche esercizio fa, se avete una disequazione del sistema che è impossibile automaticamente il sistema risulta essere impossibile. E non serve nemmeno fare lo schema dei segni.
Esercizio 15. \begin{cases} a-3 < \frac{a-5}{3} \\ (-3a)^2 +2 > (3a+1)(3a-1) \\ a(a+1) - (a-2)^2 \ge -24 \end{cases}
Qui la variabile si chiama a, come detto tante volte va trattata come se fosse una normale x. Poi notiamo nella seconda una differenza di quadrati, quindi vi applichiamo tale formula.
\begin{cases} a-3 < \frac{a-5}{3} \\ 9a^2 +2 > 9a^2 -1 \\ a^2+a - (a^2+4 -4a) \ge -24 \end{cases}
Ricordiamoci di verificare che i termini quadratici vadano via. Nella prima disequazione per eliminare la frazione, moltiplichiamo tutto per il denominatore 3!
\begin{cases} 3a-9 < a-5 \\ 0a > -3 \\ 5a \ge -20 \end{cases}
Nella seconda se ne vanno tutti i termini con la a: però scriviamo 0a che è la stessa cosa, così poi possiamo porre la domanda classica. Domanda: 0 è maggiore di -3? Sì, quindi la soluzione della seconda disequazione è per ogni a.
\begin{cases} a < 2 \\ \forall a \\ a \ge -4 \end{cases}
\forall a si disegna con una linea piena. L’intervallo comune risultante e soluzione del sistema è:
-4 \le a < 2
Abbiamo concluso la pagina riguardante i sistemi di disequazioni esercizi svolti. Trovate comunque altri centinaia di esercizi sia di matematica che di geometria analitica e geometria!
Continuate a studiare sul nostro sito!
Per approfondire con un po’ di teoria:
https://it.wikipedia.org/wiki/Sistema_di_disequazioni
esercizi
fratte