Disequazioni di primo grado: 20 ESERCIZI SVOLTI
Disequazioni di primo grado: 20 ESERCIZI SVOLTI! Le disequazioni presentano regole un po’ diverse da quelle viste per quanto riguarda le equazioni di primo grado. In questa pagina vedremo tutto ciò che serve per essere pronti al compito in classe, e saper risolvere una qualsiasi disequazione di primo grado. Presenteremo ben 20 esercizi spiegati in ogni singolo passaggio. Iniziamo subito!
Indice
- Come risolvere una disequazione
- Disequazioni: esercizi FACILI
- Disequazioni: esercizi MEDI
- Disequazioni con prodotti
- Disequazioni con parametri
Prima di cominciare con gli esercizi svolti sulle disequazioni, partiamo con il mostrare il procedimento generale che seguiremo per ogni esercizio, per trovare la soluzione di una disequazione. Vi consiglio inoltre di ripetere un attimo velocemente anche come risolvere una equazione (anche giusto i passaggi)!
Come risolvere una disequazione
Di seguito il procedimento generale da seguire. Badate bene che ci sono dei casi particolari, e piccole cose da sapere, quindi con calma fate tutti gli esercizi di almeno le prime due sezioni!
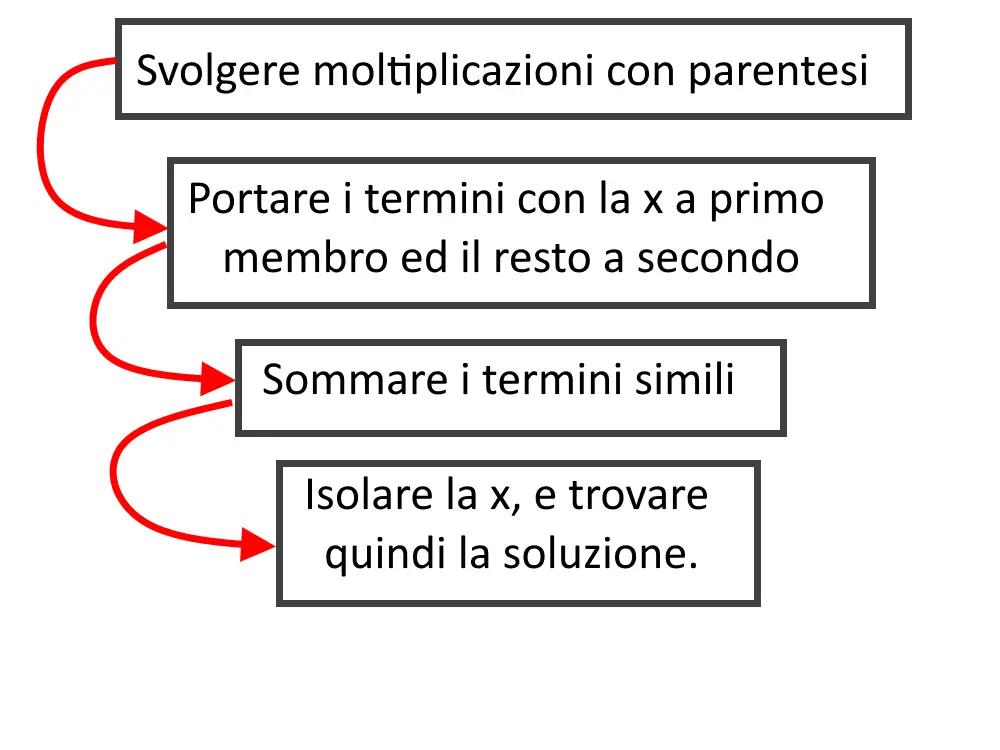
Adesso siamo pronti per iniziare a vedere degli esercizi! Essi saranno in ordine di difficoltà! Nel corso di questi esercizi, via via vedremo sempre più casi particolari e cose utilissime.
Disequazioni: esercizi FACILI
Esercizio 1. 7x \le 14
Questa è una disequazione di primo grado (ossia compaiono solamente delle x normali, NON x^2). In questo esercizio base non dobbiamo effettuare nessun passaggio di moltiplicazione, mcm o altro; di conseguenza passiamo direttamente al trovare la x. Il termine con la x (ossia 7x) già sta a sinistra e va bene! A questo punto, proprio come facevamo per le equazioni, dividiamo tutto per 7 per far rimanere la x da sola:
\frac{7x}{7} \le \frac{14}{7}
Il 7 si semplifica, ed anche la seconda frazione si semplifica. Otteniamo quindi:
x \le 2
Questa è la soluzione della disequazione.
Come potete vedere non abbiamo più una soluzione del tipo x=2, ossia una singola soluzione. Adesso, con le disequazioni, abbiamo un intervallo di soluzioni! Di fatti x \le 2 significa che tutte le x più piccole o uguali di 2 sono soluzione!
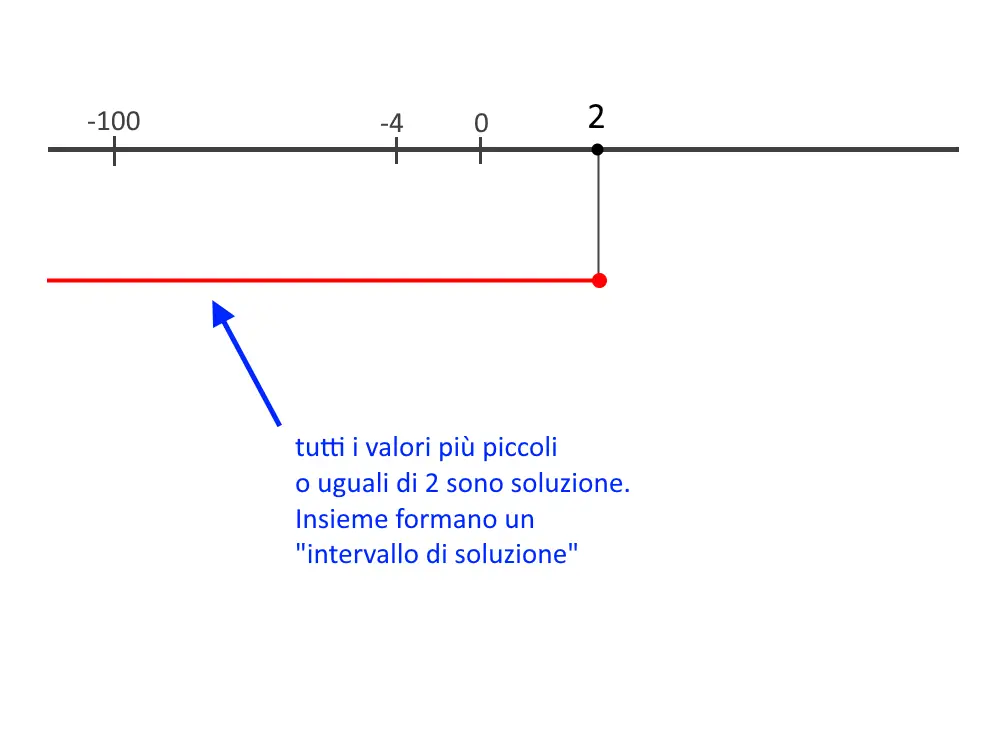
Quindi anche x=2, x=1, x=0, x=-1 x=- \frac{3}{2} ecc. sono tutte soluzioni della disequazione! Intervallo di soluzione infatti significa un insieme di soluzioni singole! Badate bene che tale intervallo è continuo chiaramente.
Esercizio 2. \frac{1}{3} x \ge 6
Anche in questo esercizio notiamo che la x è già messa a sinistra, ed a destra abbiamo solo un numero. Possiamo ricavarci direttamente la x. Questa volta però, visto che il nostro obiettivo è isolare la x e quindi levare da mezzo \frac{1}{2} , dobbiamo moltiplicare tutto per 3! Moltiplicare perché altrimenti la frazione non va via!
3 \cdotp \frac{1}{3} x \ge 3 \cdotp 6
La frazione se ne va:
x \ge 18
Abbiamo trovato qual è l’intervallo di soluzione della disequazione: in questo caso ci sta dicendo che le soluzioni sono tutti i valori di x più grandi o uguale ( \ge ) di 18! L’esercizio è finito.
Esercizio 3. -5x > 5
Qui vedremo una cosa molto importante. Come vedete il nostro obiettivo è quello di levare il -5 dalla x. Facciamo un passetto alla volta. Iniziamo a dividere tutto per 5:
- \frac{5x}{5} > \frac{5}{5}
Entrambe le frazioni vanno via, e dunque:
-x> 1
Per levare un segno meno, come facevamo per le equazioni, moltiplicavamo tutto per -1.
ATTENZIONE: quando moltiplicate o dividete tutto per un numero negativo, si inverte anche il segno stesso della disequazione!
-1 \cdotp (-x) < -1 \cdotp 1
Come potete vedere ora il segno è diventato minore (<). Ricordando che meno per meno fa più, otteniamo:
x< -1
Questo che abbiamo fatto è equivalente a “cambiare tutto di segno”. Da ora in poi cambiare tutto di segno significherà questo: cambiare tutti i termini di segno, ed in più invertire il segno della disequazione.
Continuiamo con altre disequazioni esercizi svolti!
Esercizio 4. -x \le -7
Questo è un altro esempio pratico del “cambiare tutto di segno”. Come vedete l’unica cosa che dovremmo levare dalla x è quel segno meno: di conseguenza cambiamo tutto di segno, ossia cambiamo i segni di tutti i termini che ci sono nella disequazione (sinistra e destra) ed in più invertiamo il segno della disequazione.
x \ge 7
E questa è la soluzione.
Esercizio 5. \frac{5}{7} x < 0
Esercizio molto importante!
Questo caso è l’analogo che abbiamo visto per le equazioni. Osserviamo l’esercizio: abbiamo una x a sinistra, ed a destra c’è comunque un numero, lo zero. Quindi proprio come i precedenti esercizi, facciamo lo stesso procedimento. Iniziamo a moltiplicare tutto per 7, in modo da levare la frazione dalla x:
7 \cdotp \frac{5}{7} x < 7 \cdotp 0
La frazione se ne va, e poi a destra un numero moltiplicato per 0 dà sempre 0:
5x < 0
A questo punto per levare il 5, dividiamo tutto per 5:
\frac{5x}{5} < \frac{0}{5}
Anche qui stessa cosa: 0 divido per un numero (diverso da zero) fa sempre 0. Di conseguenza la soluzione della disequazione è:
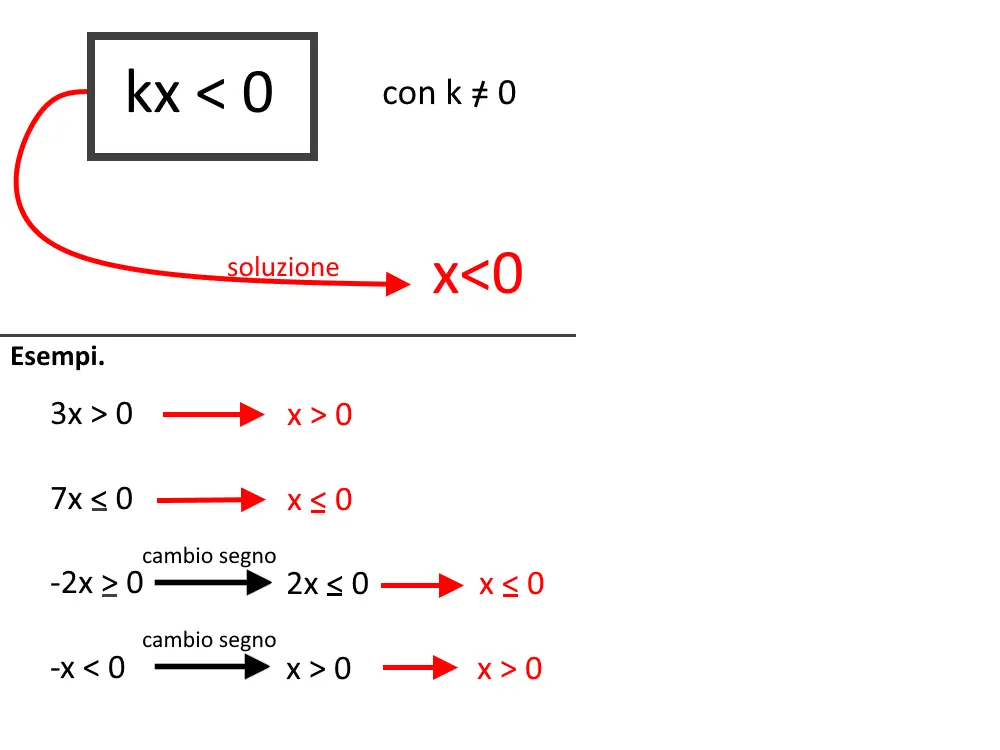
x<0
In questo esercizio abbiamo mostrato tutti i passaggi, ma voi potete direttamente giungere a tale conclusione.
Esercizio 6. -x -2 (5x+3) > 4x
Qua per la prima volta incontriamo una parentesi tonda: svogliamo assolutamente prima la moltiplicazione del -2 con questa parentesi. Ricordate che -2 moltiplica tutti i termini dentro la parentesi.
-x -10x -6 > 4x
Se vi state chiedendo perché è uscito questo: abbiamo moltiplicato per -2, quindi bisognava anche cambiare di segno al (5x+3).
Ora che non c’è nessun altra operazione da fare, portiamo tutte le x a primo membro (a sinistra) ed il resto a destra:
-x -10x -4x > 6
Così come nelle equazioni, anche nelle disequazioni quando si porta un termine da una parte all’altra il segno lo si cambia!
Sommiamo i termini con le x (quindi i coefficienti):
-15x > 6
Ed ora dividiamo per 15:
-x > \frac{6}{15}
-x > \frac{2}{5}
Ed ora cambiamo tutto di segno:
x < - \frac{2}{5}
Esercizio 7. 4(3t-1) \ge -3(t+2) -1
Qui abbiamo una t invece che la x: non c’è problema, non cambia nulla. Una variabile la potete chiamare come volete: x,y,t, “giuseppe” ecc. Quindi risolviamo la disequazione trattando la t proprio come se fosse una x! Iniziamo a risolvere le parentesi:
12t-4 \ge -3t -6 -1
Portiamo le t a primo membro, ed i numeri a secondo:
12t +3t \ge -6 -1 +4
15t \ge 3
E dividendo per 15, otteniamo la soluzione della disequazione di primo grado, in variabile t:
t \ge \frac{ 3}{15}
t \ge \frac{1}{5}
Aumentiamo un po’ la difficoltà e vediamo altri casi super importanti, cose che vi usciranno sicuramente nella verifica in classe. Vediamo ora disequazioni esercizi svolti di livello medio.
Disequazioni esercizi svolti: livello MEDIO
Esercizio 8. x+1 > 3[ 4 - 7 (x+1) ]
Qui per la prima volta in questa pagina compaiono più parentesi. La regola dice: si parte prima dalla parentesi tonda, poi si passa alla quadra ed in ultimo alla graffa se c’è. Quindi effettuiamo prima la moltiplicazione del 7 con la parentesi tonda:
x+1 > 3[ 4 - 7x -7 ]
Ora ci è rimasta la quadra, leviamo anche questa:
x+1 > 12 - 21x - 21
A questo punto siamo tornati nel punto classico degli altri esercizi, isoliamo le x a sinistra, e facciamo ciò che sappiamo già fare!
x +21x > 12 - 21 -1
22x > -10
Dividiamo tutto per 22:
x > - \frac{10}{22}
Tale frazione è semplificabile in:
x > - \frac{5}{11}
Esercizio 9. 5(x-2) - [ 3(-3x +1 ) -2 ] \ge 9x - 2( 2x-5 )
Compaiono addirittura ben 3 parentesi tonde, ma non spaventiamoci, svolgiamo prima queste con calma! Attenzione ai segni.
5x-10 - [ -9x +3 -2 ] \ge 9x - 4x + 10
Ci rimane la quadra da levarci dalle scatole. Un segno meno davanti ad una parentesi significa che dobbiamo semplicemente cambiare di segno tutti i termini che stanno dentro la parentesi.
5x-10 +9x -3 +2 \ge 9x - 4x + 10
5x +9x +4x -9x \ge 3 + 10 +10 - 2
Sommiamo a destra e sinistra, ed otteniamo alla fine:
9x \ge 21
Questo lo sappiamo fare, anzi fatelo voi! La soluzione è:
x \ge \frac{7}{3}
Continuiamo con altre disequazioni esercizi svolti!
Esercizio 10. \frac{5}{8} x +4 \ge \frac{x+3}{2} - \frac{1}{4}
Incontriamo delle frazioni, vediamo come bisogna comportarsi. Non ci sono parentesi, quindi seguendo la classica procedura, dobbiamo portare i termini con la x a primo membro, anche se sono frazioni.
\frac{5}{8}x - \frac{x+3}{2} \ge - \frac{1}{4} -4
A questo punto bisogna fare la somma come sempre. Ma, l’unica differenza è che la somma fra frazioni è un minimo comune multiplo. Effettuiamo due minimi comuni multipli distinti: uno a sinistra ed uno a destra. Otteniamo:
\frac{5x - 4(x+3) }{8} \ge \frac{-1-16}{4}
Prima di procedere con qualsiasi altra operazione, leviamo di torno quella parentesi tonda che è comparsa.
\frac{5x - 4x -12 }{8} \ge \frac{-17}{4}
E sommiamo i termini che stanno ai numeratori:
\frac{x -12 }{8} \ge \frac{-17}{4}
Ora è il momento di levare le frazioni e tornare al caso degli altri esercizi, cioè avere una disequazione semplice. Moltiplichiamo tutto per 8, così si leva sia il primo che il secondo denominatore!
x -12 \ge 2 \cdotp -17
x -12 \ge -34
E di conseguenza:
x \ge -34+12
x \ge -22
Esercizio 11. \frac{4}{5} - \frac{x+7}{10} > - (2- \frac{x+4}{2} )
Anche se vi compaiono delle frazioni non ci dobbiamo fare caso nel primo passaggio: ricordatevi che bisogna levare prima le parentesi a tutti i costi. Le parentesi rendono difficile una disequazione, levarle significa rendere più semplice e risolvibile un esercizio di disequazione di primo grado.
\frac{4}{5} - \frac{x+7}{10} > - 2+ \frac{x+4}{2}
- \frac{x+7}{10} - \frac{x+4}{2} > - 2 -\frac{4}{5}
Ed ora facciamo due minimi comuni multipli (quindi la somma) a sinistra e destra separatamente.
\frac{-(x+7) - 5 (x+4) }{10} > \frac{-10 - 4}{5}
Semplifichiamo la forma del primo numeratore:
\frac{-x-7 - 5x - 20 }{10} > \frac{-14}{5}
\frac{ - 6x - 27 }{10} > \frac{-14}{5}
Ai numeratori non possiamo fare più nulla per rendere più semplice ancora la forma delle frazioni, quindi è giunto il momento di levare i denominatori moltiplicando tutto per 10!
- 6x - 27 > -28
- 6x > -28 +27
E perciò:
- 6x > -1
Cambiamo tutto di segno (e quindi invertiamo anche il >), e dividiamo per 6, ed abbiamo finalmente finito l’esercizio.
x < \frac{1}{6}
Continuiamo con altre disequazioni esercizi svolti!
Esercizio 12. 5x - 3x(x+1) + 4 \le (x-1)^2 - (2x-1)^2
Esercizio molto importante: vedremo la soluzione “impossibile”. Come possiamo vedere, salta all’occhio il quadrato del binomio, che ha come formula la seguente.
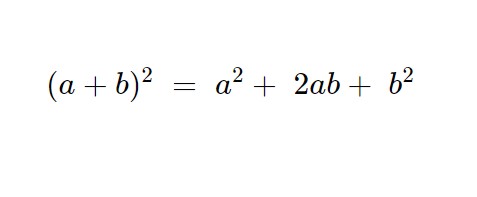
Utilizzando questa formula nei due quadrati a destra, e levando la prima parentesi a sinistra:
5x - 3x^2 -3x + 4 \le x^2 + 1 -2x - (4x^2 +1 -4x )
Leviamo anche l’ultima parentesi:
5x - 3x^2 -3x + 4 \le x^2 + 1 -2x -4x^2 -1 +4x
Compaiono dei termini quadratici. Visto che stiamo sempre nel caso delle disequazioni di primo grado, questi termini se ne dovranno andare via prima o poi. Di fatti se portiamo i termini con le x (quindi anche quelli con x^2):
5x - 3x^2 -3x -4x -x^2 +2x +4x^2 \le + 1 -1 -4
Sommando ritorna ad essere una disequazione di primo grado, ottimo! Ricordate che si sommano i termini con la x, e poi separatamente quelli quadratici.
0x \le -4
Anzi, addirittura otteniamo un qualcosa di davvero strano e particolare: non c’è più nessun termine con la x, per questo scriviamo 0x.
Ora per risolvere questo caso particolare dobbiamo porci la domanda seguente: 0 è più piccolo o uguale di -4? La risposta è no, non è più piccolo. Di conseguenza tale disequazione non sarà MAI verificata, perché per qualsiasi x, moltiplicata per 0 darà sempre 0, e quindi risulterà sempre 0 \le -4 ma ciò è impossibile!
La disequazione non ha soluzione o si dice che è impossibile.
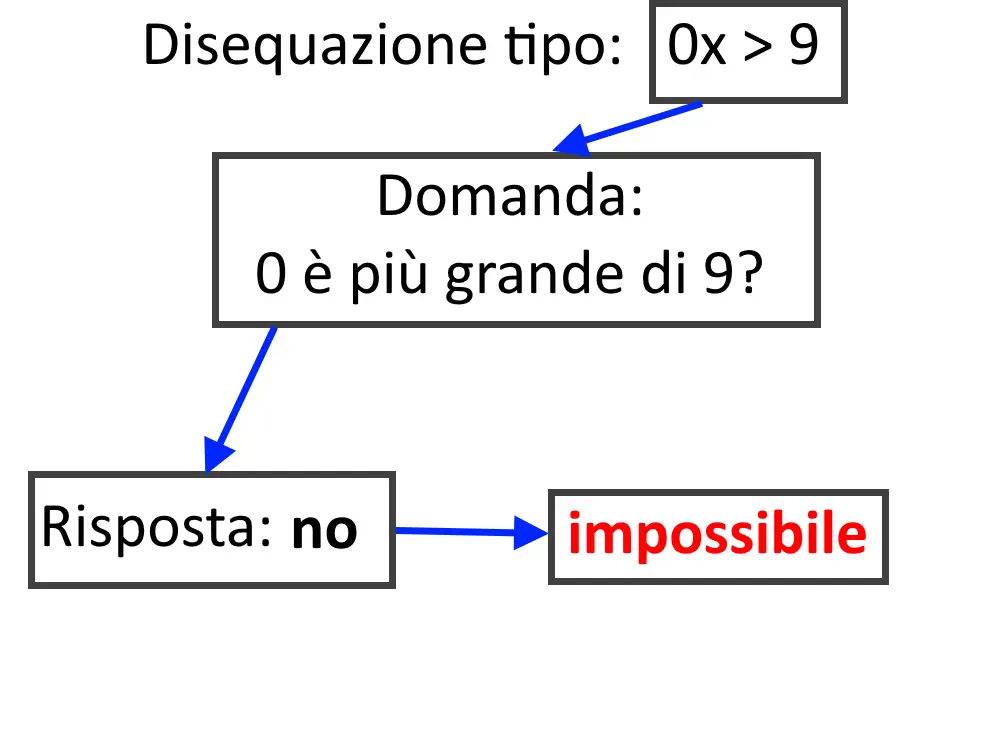
Per approfondire: quando una disequazione è impossibile?
Esercizio 13. (2b+3)(3-2b) \le -(-2b)^2 + 1
Partiamo col notare che la variabile qui si chiama b, e non cambia nulla abbiamo detto. Poi, se mettiamo un segno meno in evidenza nella seconda parentesi diventa:
(2b+3)(-(2b-3)) \le -(-2b)^2 + 1
Ora quel meno possiamo portarlo al di fuori della parentesi:
-(2b+3)(2b-3) \le -(-2b)^2 + 1
E ciò l’abbiamo fatto perché così è comparsa la formula della differenza di quadrati.
Così, usando un occhio critico, ci siamo risparmiati un bel po’ di calcoli, perché di fatti seguendo la formula otteniamo:
-(4b^2 - 9) \le -(4b^2) + 1
Compaiono dei termini quadratici. Come detto prima, come prova dovranno levarsi, e di fatti:
-4b^2 + 9 \le -4b^2 + 1
Portiamo a primo membro le b:
-4b^2 + 4b^2 \le + 1-9
Ed infatti se ne vanno via, rimane perciò:
0b \le -8
In una disequazione la variabile ci deve sempre stare, quindi la scriviamo mettendoci uno zero vicino, visto che si annulla.
Adesso ci dobbiamo porre sempre la domanda seguente: 0 è più piccolo o uguale di -8? Ovviamente no, perché 0 è più grande. Di conseguenza la disequazione non è mai verificata. La disequazione non ha soluzione e si dice:
impossibile
Continuiamo con altre disequazioni esercizi svolti!
Esercizio 14. (x-5)(x+5) - 2(1-6x) \ge (1-x)^2 +7 (2x-5)
Qui balza all’occhio sia la differenza di quadrati subito all’inizio, e poi anche un quadrato di un binomio. Applichiamo le formule:
x^2 -25 - 2+12x \ge 1+x^2 -2x +14x-35
Portiamo le x a primo membro, e come prova che stiamo facendo bene i termini quadratici se ne dovranno andare.
x^2 +12x -x^2 +2x -14x \ge 1-35 +25+2
E di fatti si ritorna sempre ad una disequazione di primo grado.
0x \ge -7
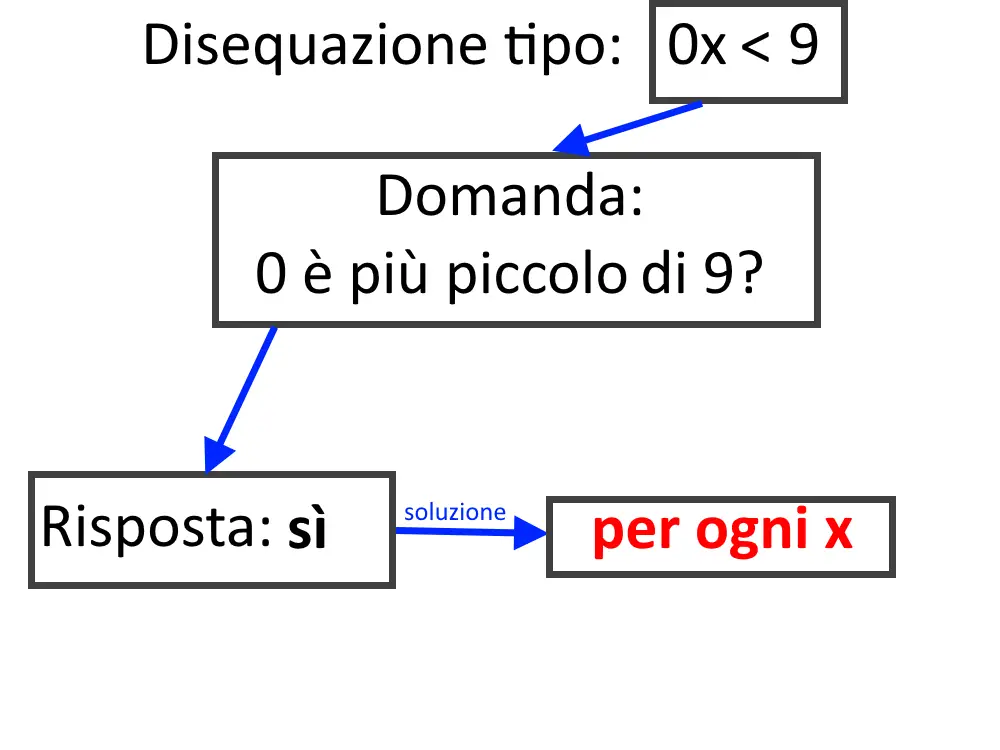
Otteniamo ancora una volta uno 0 vicino alla x. Ci dobbiamo porre la domanda: lo 0 è più grande o uguale di -7? Beh sì, lo 0 è più grande! Quindi la disequazione per qualsiasi x diventa sempre:
0 \ge -7
E questa è sempre verificata! Cioè è vera! Ciò che dice tale disequazione è vero, quindi la disequazione ha come soluzione una qualsiasi x. Diremo che la soluzione è:
\forall x
Esercizio 15. \frac{x- \frac{1}{3} }{4} - \frac{7x}{\frac{1}{4} +5 } - \frac{1}{4}x \le x
Vi sono delle frazioni anche all’interno di un numeratore e di un denominatore: per cui svolgiamo dei minimi comuni multipli solo all’interno di questi.
\frac{ \frac{3x-1}{3} }{4} - \frac{7x}{\frac{1+20}{4} } - \frac{1}{4}x \le x
\frac{ \frac{3x-1}{3} }{4} - \frac{7x}{\frac{21}{4} } - \frac{1}{4}x \le x
Vi sono due frazioni di frazioni. Le frazioni di frazioni le si possono trasformare in semplici frazioni con il seguente procedimento: si moltiplica il numeratore con l’inverso del denominatore. Nel nostro caso:
\frac{3x-1}{3} \cdotp \frac{1}{4} - 7x \cdotp \frac{4}{21} - \frac{1}{4}x \le x
Moltiplichiamo numeratore per numeratore, e denominatore per denominatore:
\frac{3x-1}{12} - \frac{28x}{21} - \frac{1}{4}x \le x
Possiamo eliminare i denominatori. Facendo il massimo comune divisore fra i denominatori (12,21,4), otteniamo un 84. Moltiplichiamo tutto per 84:
7(3x-1) - 4\cdotp 28x - 21x \le 84x
21x-7 - 112x - 21x \le 84x
E risolviamo come sappiamo già fare:
-196x \le 7
Isoliamo la x chiaramente (cambiamo di segno e dividiamo per 196):
x \ge - \frac{1}{28}
Adesso concludiamo con degli esercizi svolti sulle disequazioni di primo grado con prodotti!
Esercizi sulle disequazioni con PRODOTTI
Esercizio 16. (x-3)(x+7) < 0
Questa è una disequazione con prodotto, ossia vi è un prodotto (e nient’altro) a sinistra, ed a destra abbiamo uno 0. Esso si risolve con un falso sistema.
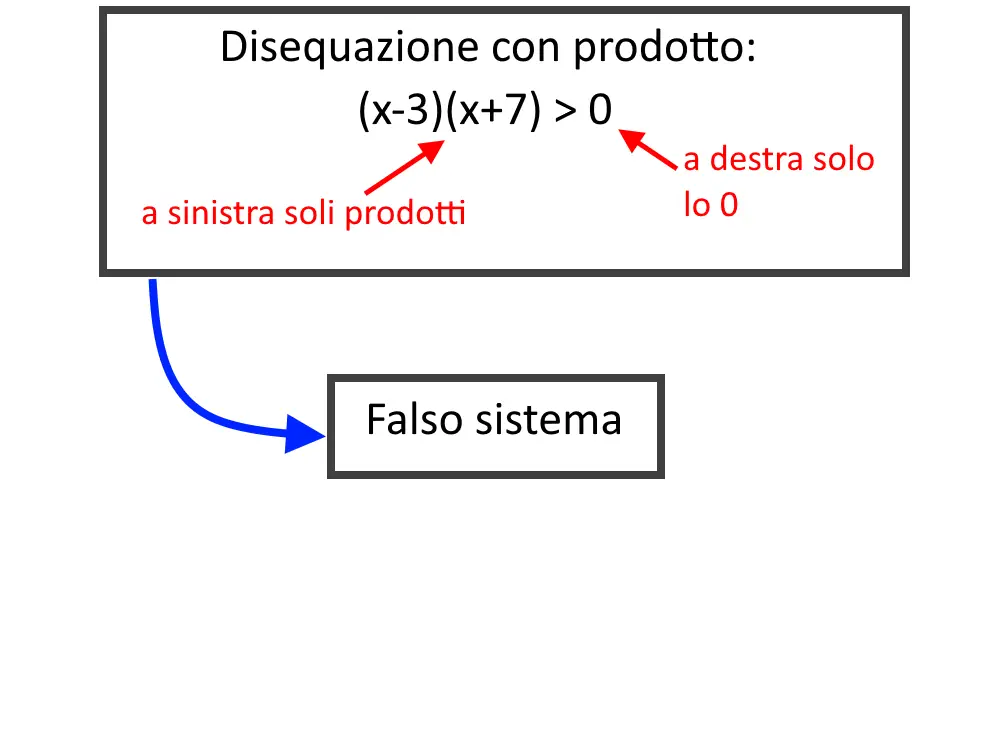
Il falso sistema si scrive disegnando due linee verticali, e poi in ogni rigo mettiamo un termine del prodotto. Per ogni rigo mettiamo lo stesso segno della disequazione.
\big\| x-3 < 0 \\ \big\| x+7 < 0
A questo punto risolviamo separatamente le due disequazioni:
\big\| x < 3 \\ \big\| x < -7
Arrivati a questo punto, bisogna disegnare il grafico delle disequazioni (detto anche quadro dei segni). Cliccateci sopra per capire bene tutti i casi. In breve: disegniamo una retta con i punti -7 e 3, segniamo gli intervalli che indicano i due righi. Poi segniamo con un segno + le parti continue, e con un segno – le parti tratteggiate. Facciamo il prodotto dei segni (come meno per meno fa più) per ogni sezione. La soluzione sarà l’intervallo negativo, se la disequazione iniziale (prima del falso sistema) ha un segno minore. Altrimenti il contrario. Inoltre, visto che è solo minore (<) ci mettiamo un pallino vuoto, per ricordarci di non prendere quel singolo valore.
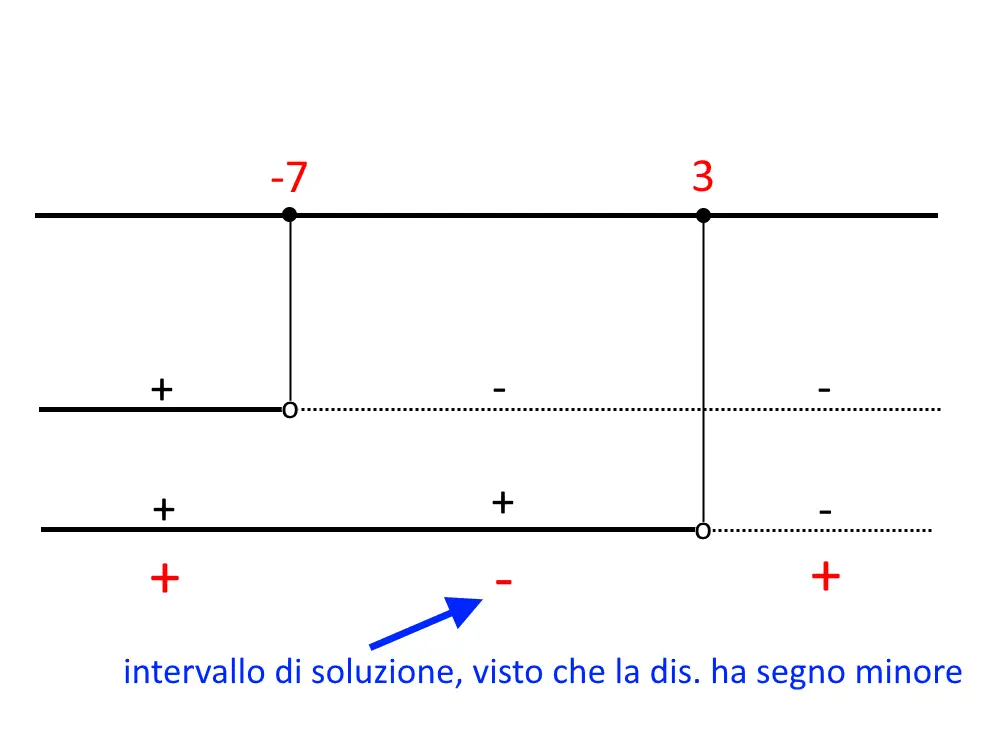
Nel nostro caso la soluzione è l’intervallo:
-7<x<3
Esercizio 17. -x (2-x) < 0
Altra disequazione con prodotto: falso sistema.
\big\| -x < 0 \\ \big\| 2-x < 0
Nella prima cambiamo di segno, la seconda la risolviamo.
\big\| x > 0 \\ \big\| x > 2
Disegniamo il grafico delle disequazioni, o schema dei segni.
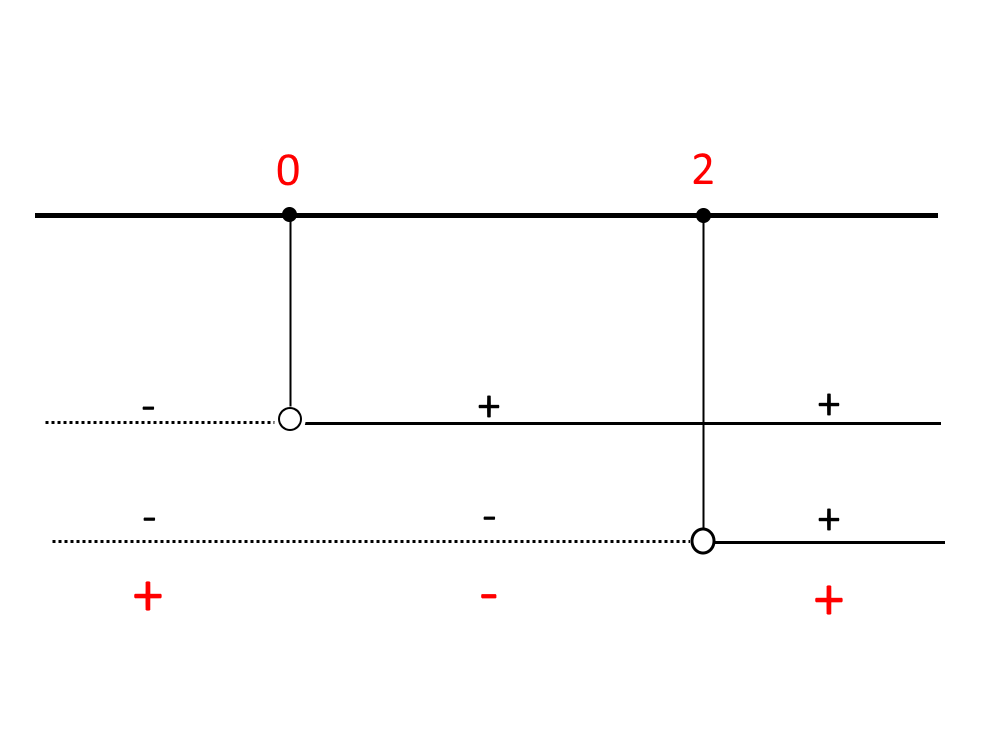
La disequazione presenta un segno minore, quindi prendiamo la parte negativa come soluzione:
0<x<2
Continuiamo con altre disequazioni esercizi svolti!
Esercizio 18. (3x-6)(x+4) > 0
Sempre falso sistema:
\big\| 3x-6 > 0 \\ \big\| x+4 > 0
\big\| x > 2 \\ \big\| x > -4
Disegniamo il grafico dei segni, prendiamo poi gli intervalli positivi, che sono due.
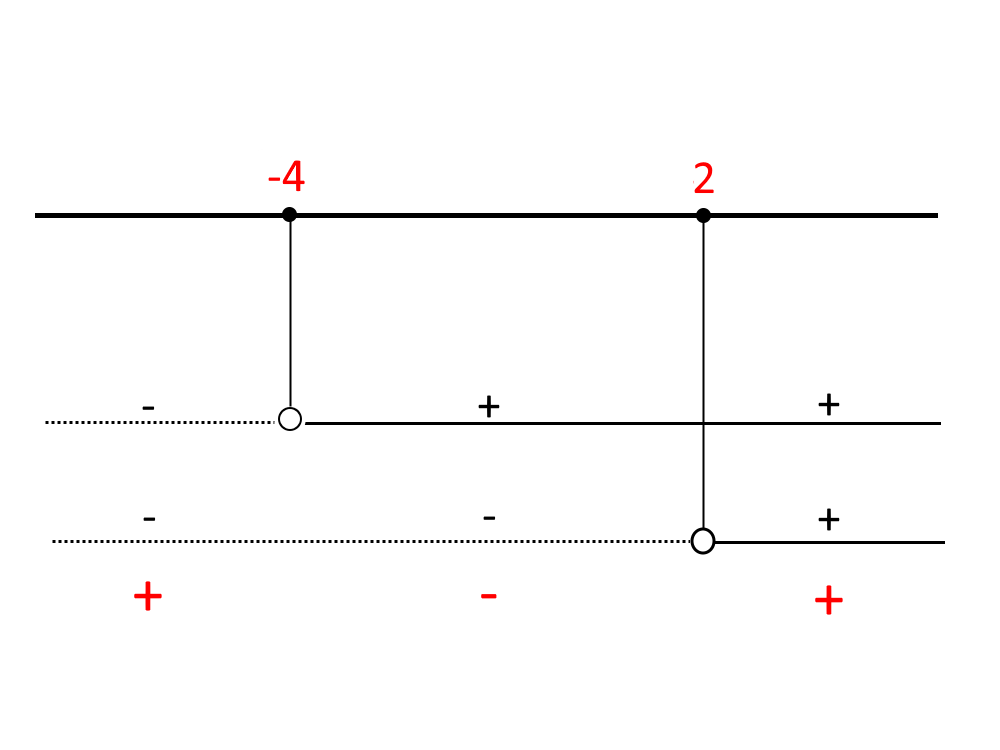
La soluzione è l’unione:
x<-4 \lor x> 2
Esercizio 19. 2x (x+1)(3-x) \le 0
Qui abbiamo invece ben 3 prodotti, il senso rimane lo stesso, ossia scriviamo sempre un falso sistema ma con tre righi.
\big\| 2x \le 0 \\ \big\| x+1 \le 0 \\ \big\| 3-x \le 0
\big\| x \le 0 \\ \big\| x \le -1 \\ \big\| x \ge 3
Disegniamo un grafico della disequazione con tre righi, dove mettiamo poi pallini pieni per ricordarci che si possono prendere quei punti.
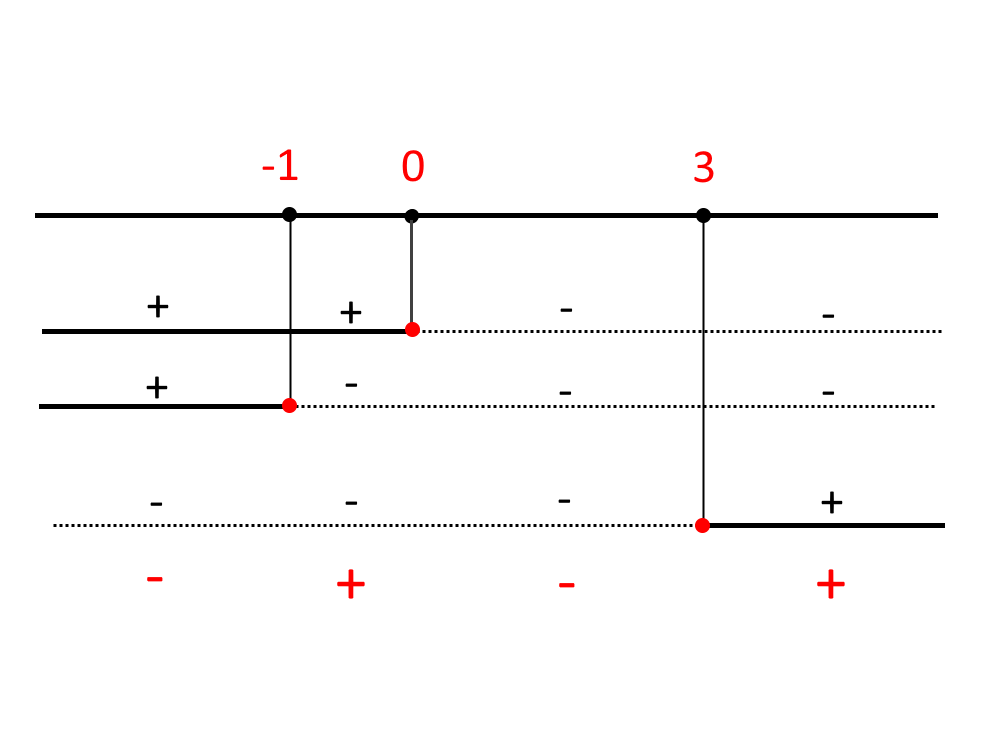
La soluzione sono gli intervalli con il -, ossia:
-1 \le x \le 0 \lor x \ge 3
Vediamo l’ultima cosuccia, cioè quando si ha a che fare con la presenza di un parametro!
Disequazioni con parametri
Esercizio 20. Trovare il valore da dare al parametro a affinché la seguente disequazione risulti avere come soluzione x>0.
3(x-2) > 4a - 2
L’obiettivo è arrivare ad avere x>0. Quindi iniziamo a svolgere la disequazione, portandoci ad avere solo la x a sinistra.
3x-6 > 4a - 2
3x > 4a - 2 +6
E poi dividiamo per 3 ed abbiamo la x da sola (quindi già abbiamo un pezzo di x>0):
x > \frac{4a - 2 +6}{3}
Adesso l’unica cosa che manca per avere x>0 è che la parte di destra, per confronto, deve essere uguale a zero. Ciò è equivalente a risolvere una equazione nell’incognita a:
\frac{4a - 2 +6}{3} = 0
Moltiplichiamo per 3 dunque:
4a - 2 +6 = 0
4a = 2 -6
Sommiamo e otteniamo quindi a. Ed abbiamo fatto!
4a = -4 \implies a=-1
Finalmente questa lunga pagina su esercizi disequazioni di primo grado è conclusa. Abbiamo imparato molto. Trovate altre centinaia di esercizi di qualsiasi argomento di matematica, geometria analitica e geometria!
Per approfondire:
https://it.wikipedia.org/wiki/Disequazione
verifica
equazioni
disequazioni
esercizi