Come fare il grafico delle disequazioni
Come fare il grafico delle disequazioni. Detto anche schema o quadro dei segni, è tipico di quasi ogni esercizio riguardante le disequazioni. In questa pagina vi spiegheremo passo dopo passo come si fanno, e vedremo insieme più casi dove esso va disegnato e applicato. Capiremo poi che intervalli prendere come soluzione. I tre casi base in cui vi capiterà di disegnare grafici di disequazioni sono i seguenti.
Indice
- Grafico di una disequazione di primo grado
- Grafico di una disequazione fratta
- Grafico di un sistema di disequazioni
Partiamo col caso base, quello di una semplice equazione lineare di primo grado.
Grafico di una disequazione di primo grado
Per non confonderci, inquadriamo un secondo la situazione. Una disequazione di primo grado è un qualcosa del tipo:
3x > 2
In una disequazione di questo tipo non bisogna disegnare nulla, semplicemente si divide tutto per te e si ha la soluzione:
x > \frac{2}{3}
Invece, quando si ha a che fare con un prodotto si disegna! Cioè quando la disequazione è formata da SOLI prodotti a primo membro ( a sinistra ), allora lì sì che bisogna fare un quadro dei segni (o grafico, come volete chiamarlo).
Di fatti, consideriamo una disequazione di questo tipo:
x(x-2) > 0
Come potete notare, questa disequazione è formata da un primo membro (la parte sinistra) fatto solo di prodotti, mentre cosa importante: a destra c’è solo lo zero. Questa si risolve con un falso sistema, ossia un sistema in cui in ogni rigo si scrive un pezzo di tale prodotto, come segue:
\big\| x > 0 \\ \big\| x-2 > 0
Il primo rigo è una disequazione già risolta. Il secondo rigo basta portare il -2 a destra:
\big\| x > 0 \\ \big\| x > 2
Ora che tutti i righi del falso sistema sono risolti, per trovare la soluzione, dobbiamo disegnare il grafico della disequazione o schema dei segni!
Di seguito il procedimento che bisogna seguire per tracciare un buon grafico delle disequazioni.
Disegniamo una linea retta con i numeri che ci sono nel falso sistema.
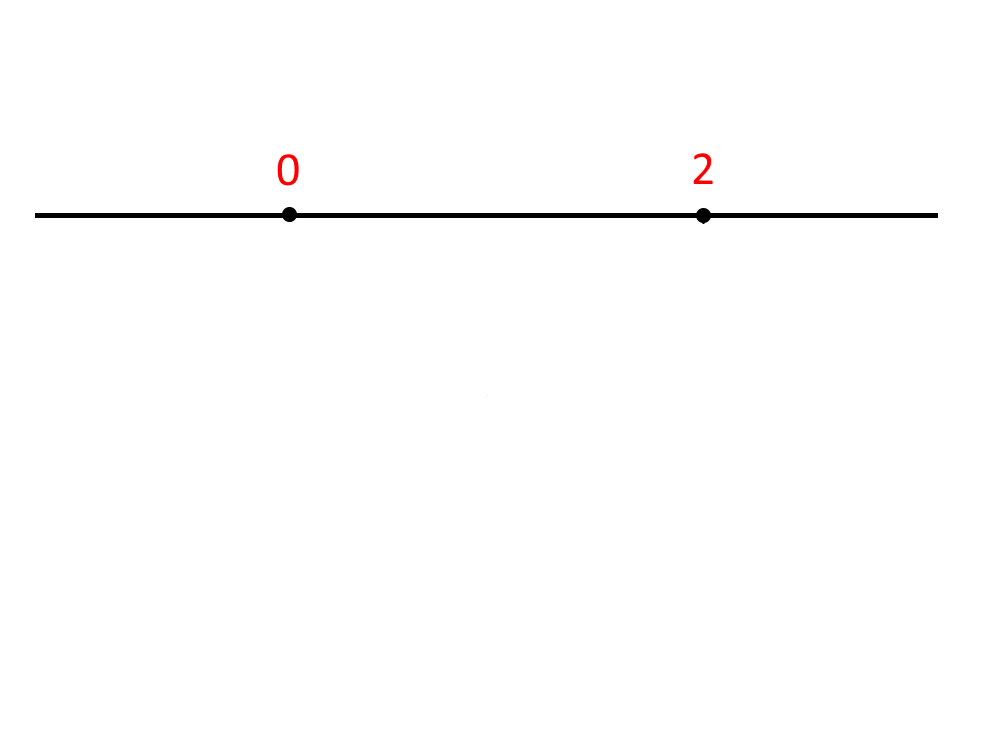
Tracciamo due linee che ricoprono gli intervalli che dicono le due disequazioni, il restante lo tratteggiamo.
Quindi, ad esempio x>0 significa che dobbiamo prendere come intervallo tutto quello che è più grande di 0, e lo disegniamo in un rigo. Nel secondo rigo disegniamo x>2, cioè tutto quello più grande di 2. Inoltre, mettiamo un pallino vuoto per ricordarci che è solo un maggiore (>) e quindi tali punti non dobbiamo prenderli dopo. Se ci fosse stato \ge mettevamo dei pallini pieni.
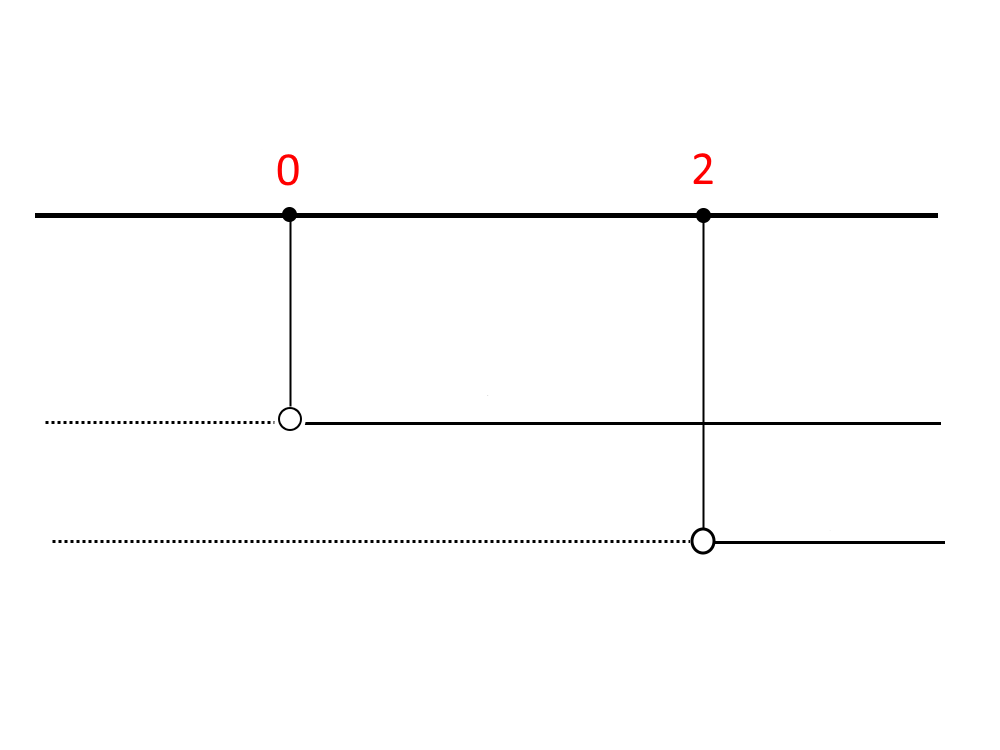
Mettiamo un segno + sugli intervalli continui, un segno – sugli intervalli tratteggiati.
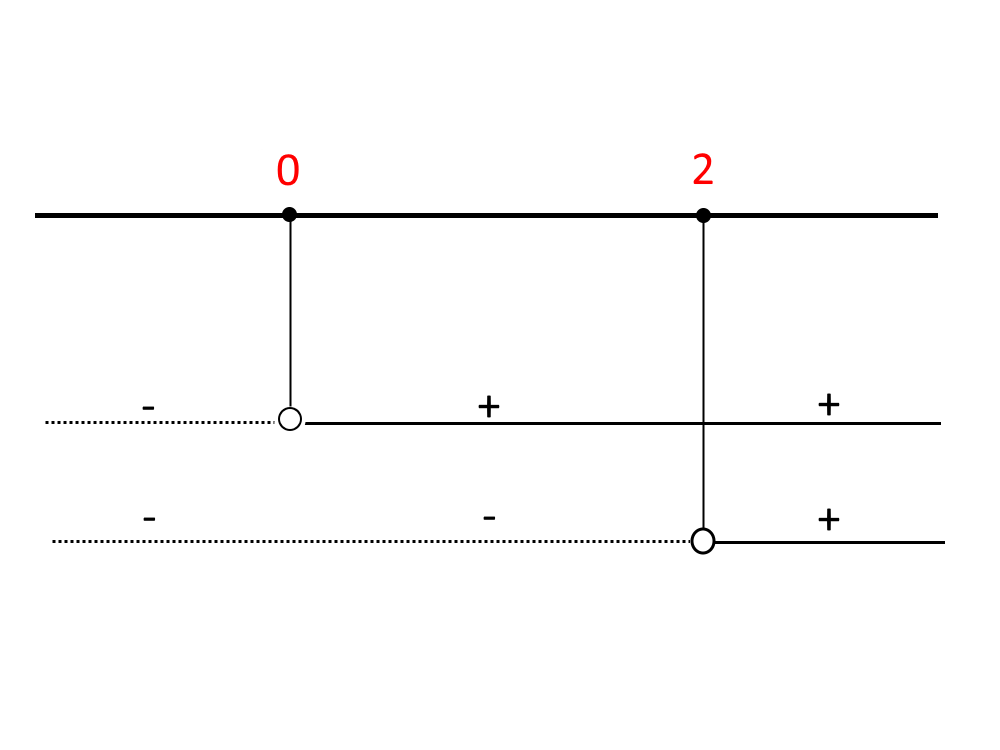
Facciamo la regola del segno e scriviamo il segno risultante (come ad esempio + per – fa -).
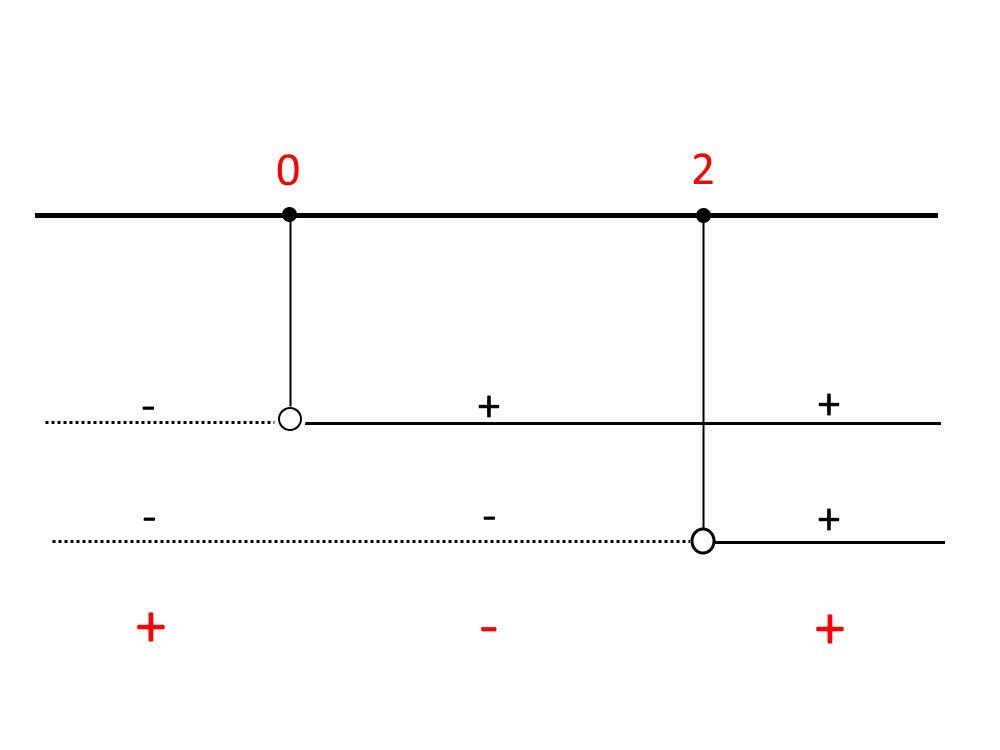
Prendiamo come soluzione lo stesso segno della disequazione di partenza (cioè quella prima di scrivere il falso sistema), ad esempio se la disequazione ha un maggiore (>) allora si prendono gli intervalli positivi. Se ha un minore (<) si prendono come soluzione gli intervalli negativi.
La soluzione quindi, in questo caso, sono gli intervalli col segno +, perché la disequazione iniziale ha segno maggiore (>). La soluzione è:
x<0 \lor x>2
Quel simbolo è per indicare che stiamo unendo due intervalli (vi capiterà spesso di doverlo usare).
Esempio 1. (x-2)(x+1) <0
In quest’altro esempio vi è ancora una volta una disequazione lineare, in cui figura un prodotto fra due termini, e null’altro. Questo si risolve con un falso sistema, e disegnando il grafico dei segni dopo.
\big\| x-2 > 0 \\ \big\| x+1 > 0
Isoliamo la x a sinistra in ogni rigo:
\big\| x > 2 \\ \big\| x > -1
Ora siamo pronti per disegnare lo schema dei segni di questo falso sistema. Seguendo lo stesso procedimento di prima otteniamo:
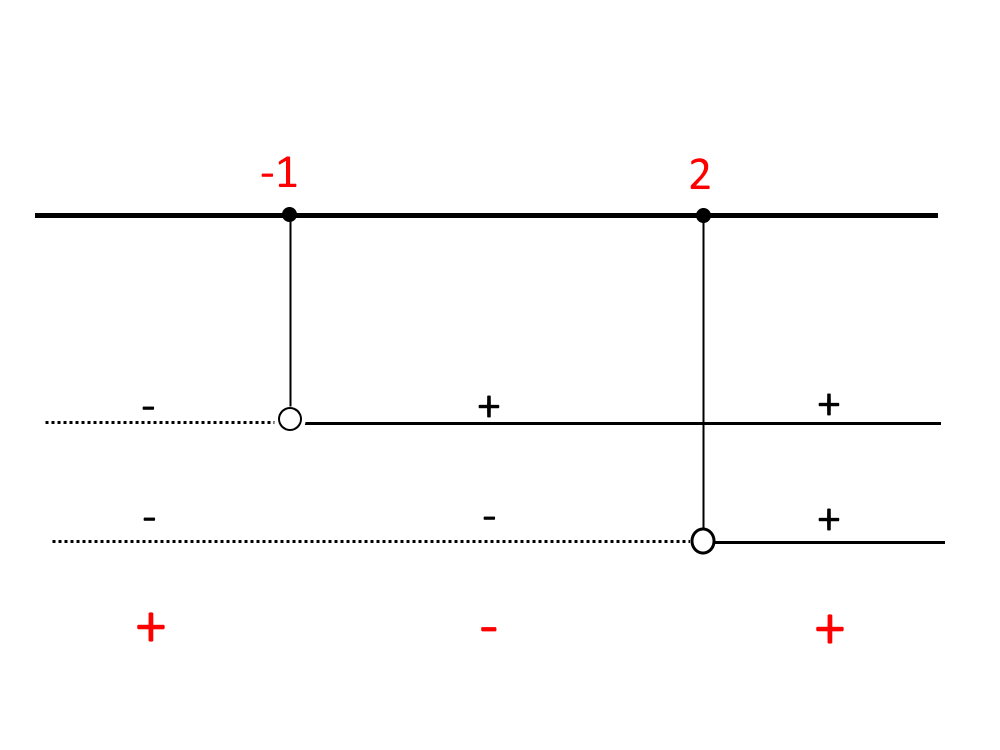
E visto che la disequazione iniziale (quella prima del falso sistema) presenta un segno minore, allora la soluzione sarà l’intervallo negativo col segno -!
-1<x<2
Nulla di così impossibile!
Grafico di una disequazione fratta
Qui vi si apre tutta una gigante parentesi sulle disequazioni fratte. Noi qui siamo interessati solo al grafico che ne esce fuori. Questo, come detto, è un altro caso in cui vi servirà tracciare lo schema dei segni di una disequazione. Abbiamo a che fare con un qualcosa del tipo:
\frac{-x+3}{x} \ge 0
Analogamente al prodotto, qui abbiamo tutti i termini che fanno parte di una frazione, e si risolve scrivendo un falso sistema.
\big\| -x+3 \ge 0 \\ \big\| x > 0
Nel secondo rigo, per via delle condizioni di esistenza, non ci va mai l’uguale. Per approfondire: disequazioni fratte.
\big\| -x \ge -3 \\ \big\| x > 0
\big\| x \le 3 \\ \big\| x > 0
Seguiamo lo stesso procedimento discusso all’inizio e disegniamo il suo grafico. Teniamo a mente però che nel rigo riguardante il x \le 3 ci andrà un pallino pieno, visto che c’è anche l’uguale. Tenete a mente che non serve scrivere i righi del grafico in ordine con i righi del falso sistema!
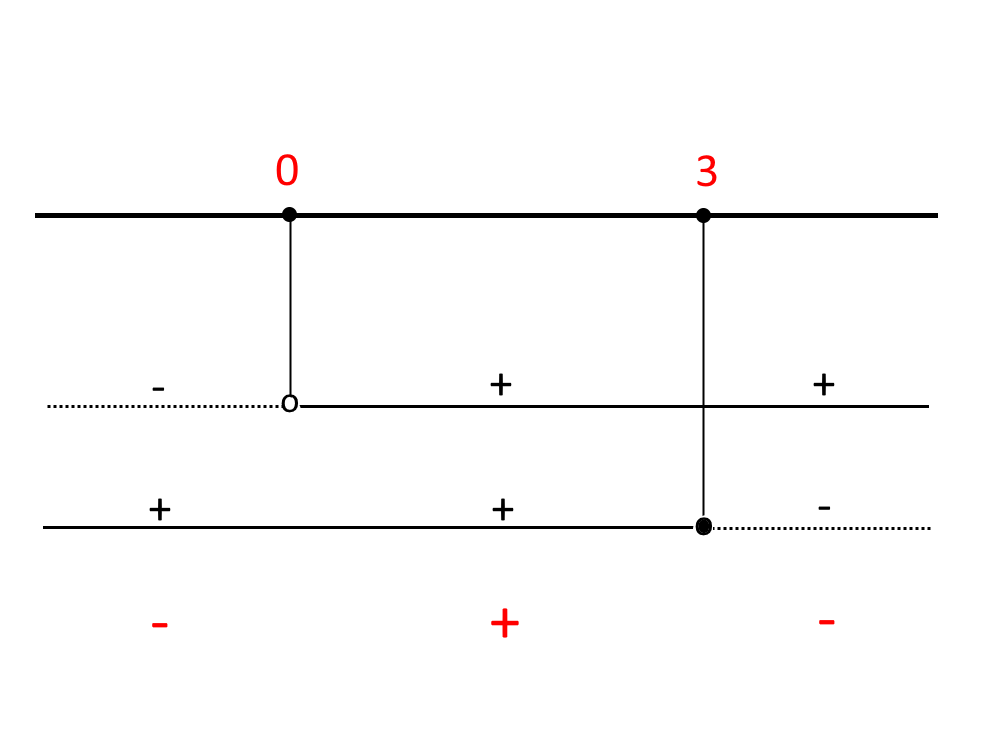
La soluzione sarà l’intervallo positivo, per cui:
0<x \le 3
Visto il pallino pieno, prendiamo anche il 3 come soluzione, mettendoci l’uguale!
Occorre prestare molta attenzione col prossimo capitoletto!
Come disegnare un SISTEMA di disequazioni
Su questo è molto facile confondersi e sbagliare! Per questo è importantissima questa sezione! Fino ad ora abbiamo visto come disegnare un grafico…che è relativo ad un falso sistema! Il sistema di disequazioni è un’altra cosa!
Sistema significa prendere gli intervalli comuni, quindi semplicemente vedere quali intervalli si sovrappongono, tutto qui.
Esempio. \begin{cases} x>0 \\ x < 5 \end{cases}
Qui dobbiamo solamente tracciare una linea e i due intervalli, senza linee tratteggiate, senza segni, senza nient’altro.
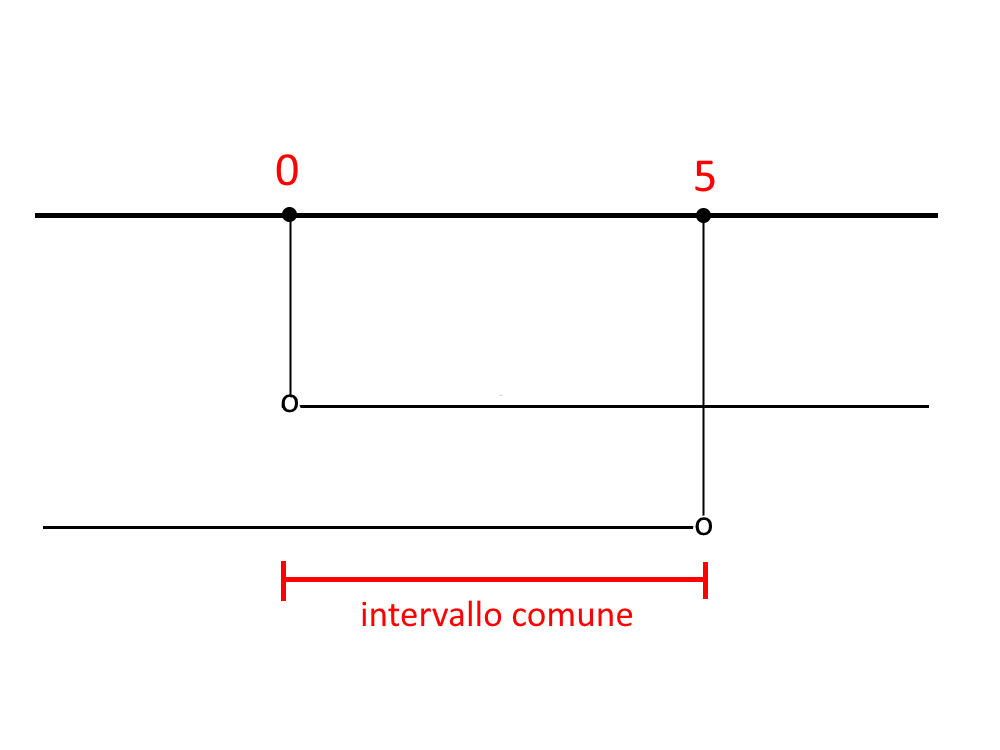
L’unica cosa da fare è vedere quale porzione di intervallo è comune, ossia si sovrappone, cioè è uguale al primo rigo ed al secondo. Come vedete da questo esempio è la porzione seguente:
0<x<5
Che è anche la soluzione poi del sistema!
Abbiamo imparato come fare il grafico delle disequazioni.
Se volete approfondire il discorso delle disequazioni:
- Sistema di disequazioni
- Disequazioni fratte
- Disequazioni di secondo grado
- Quando una disequazione è impossibile?
Trovate altre centinaia di esercizi svolti e argomenti sul nostro sito sia di matematica che di geometria analitica e geometria!
Per approfondire:
https://it.wikipedia.org/wiki/Disequazione
fratte
esercizi