Disequazioni goniometriche ESERCIZI SVOLTI

Disequazioni goniometriche: ESERCIZI SVOLTI! In questa pagina vedremo spiegati passo dopo passo degli esercizi svolti disequazioni goniometriche! Basterà una sola giornata su questa pagina per prepararsi alla verifica in classe! Prima però vi consiglio assolutamente di rivedere e ripetere un attimino come si risolvono le equazioni goniometriche elementari e e le equazioni goniometriche in generale. Iniziamo subito!

Indice

• Disequazioni goniometriche elementari
• Disequazioni goniometriche riconducibili a quelle elementari
• Disequazioni goniometriche lineari

Iniziamo subito a vedere esercizi svolti disequazioni goniometriche elementari!

Disequazioni goniometriche ELEMENTARI

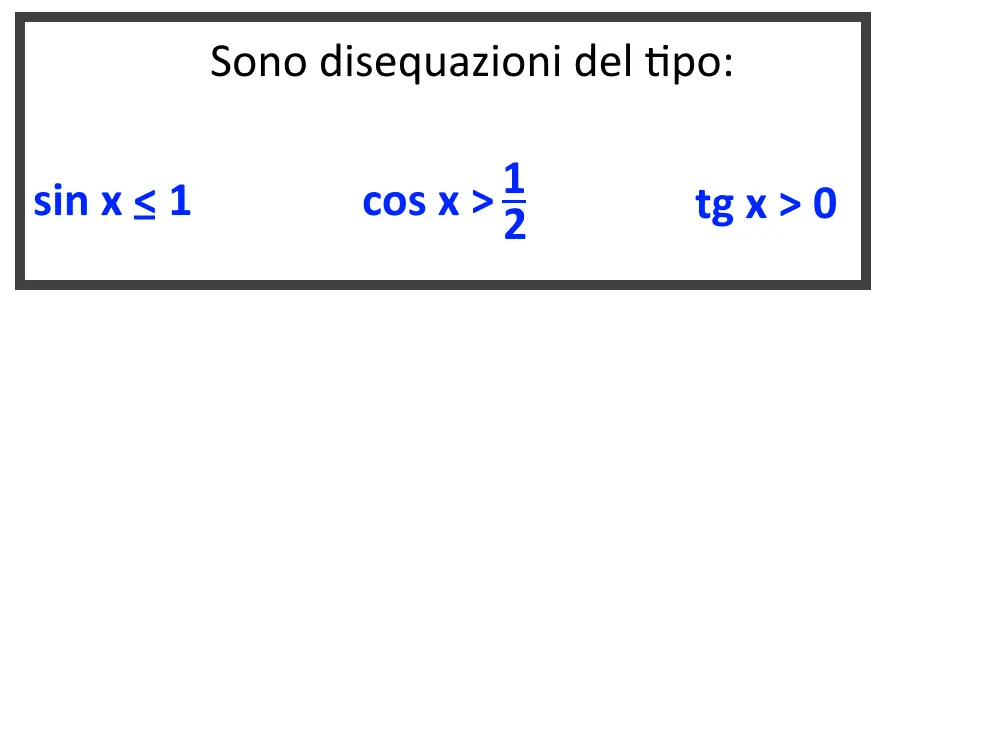
Esercizio 1. 2 \sin x > \sqrt{2}


Questa è una disequazione goniometrica elementare, ossia abbiamo una funzione (seno) da sola e nient’altro. I punti principali rimangono bene o male gli stessi delle equazioni goniometriche elementari: quindi andiamo ad isolare il seno per prima cosa.

\sin x > \frac{ \sqrt{2} }{2}

A questo punto, dopo che la funzione seno è isolata. Andiamo a disegnare la circonferenza goniometrica, ed andiamo a segnare la retta orizzontale Y= \frac{ \sqrt{2} }{2} . Ricordatevi che per il seno la retta da disegnare è orizzontale!

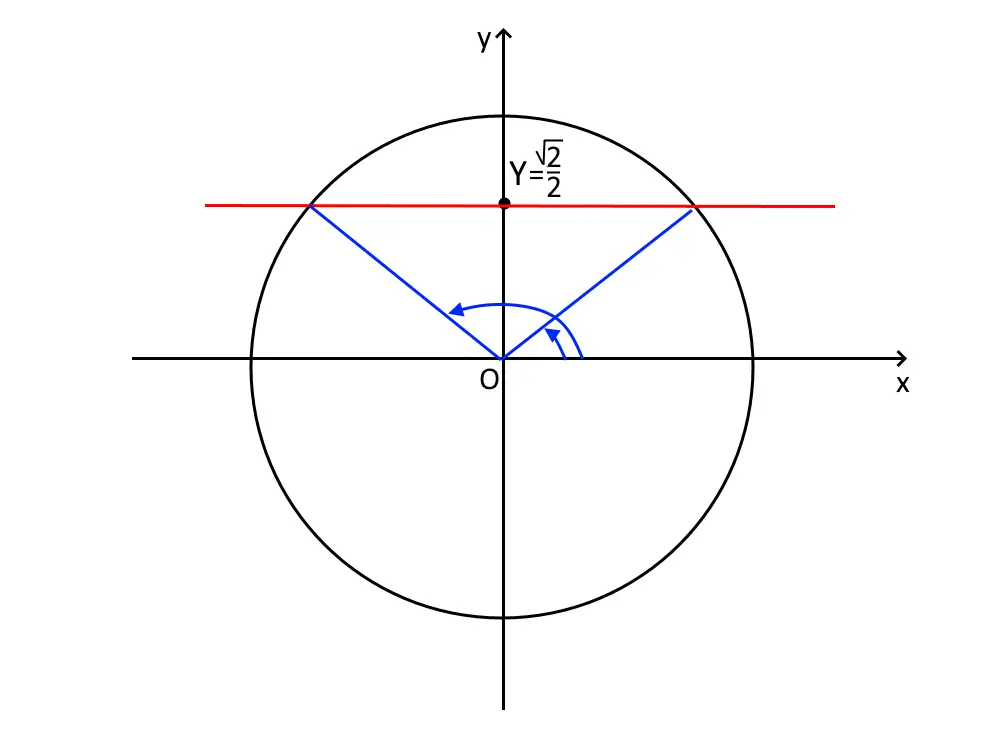
La disequazione ci dice \sin x > \frac{ \sqrt{2} }{2} : ossia ci sta dicendo che dobbiamo prendere tutti i valori del seno che sono superiori a \frac{ \sqrt{2} }{2} .

In pratica andiamo ad evidenziare tutto l’intervallo di circonferenza (e quindi di angoli) che stanno sopra la retta Y= \frac{ \sqrt{2} }{2} !

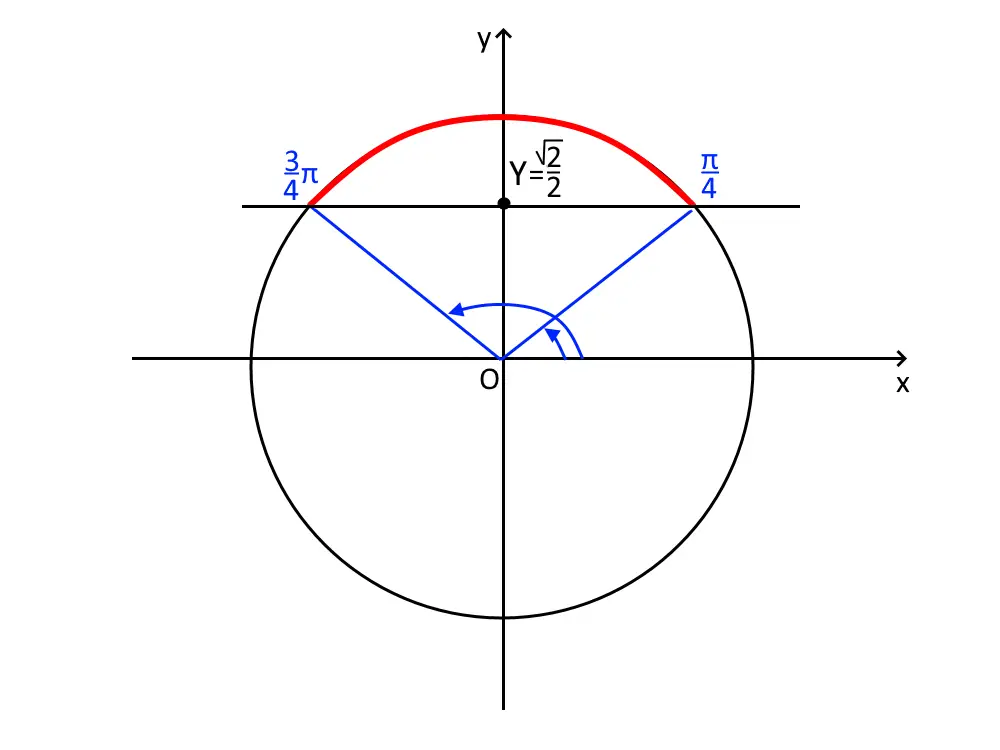
La soluzione è quindi tutto l’intervallo evidenziato! Come facciamo a sapere qual è di preciso? Come vedete dal disegno, la soluzione sarà un qualcosa del tipo: ... < x < .... Come calcoliamo questi due angoli? Proprio con lo stesso ragionamento fatto per le equazioni goniometriche elementari: questi due angoli hanno il \sin x = \frac{ \sqrt{2} }{2} e quindi basterà prendere mano alla calcolatrice: shift e poi scrivere \sqrt{2} : 2 . La calcolatrice ci dirà il primo angolo:

45°=\frac{\pi}{4}

Aggiungiamo poi la periodicità del seno, e quindi il primo estremo sarà:

\frac{\pi}{4} +2k \pi

Ora dobbiamo trovare l’altro angolo. Come già fatto per altri esercizi, andiamo a vedere la figura (bisogna andare per ragionamento) e notiamo che l’altro angolo risulta essere 180°-45°:

\pi - \frac{\pi}{4} = \frac{3}{4} \pi

A cui poi andiamo, come sempre, ad aggiungere la periodicità del seno. Quindi la soluzione dell’esercizio:

\frac{\pi}{4} +2k \pi < x < \frac{3}{4} \pi + 2 k \pi

Esercizio 2. \cos x \ge 0


In linea generale il procedimento di questo esercizio, che è simile al precedente, è lo stesso. C’è una differenza che ora vedremo però. Come possiamo vedere è una disequazione goniometrica elementare: c’è il coseno e nessun’altra funzione. Il coseno è già isolato a sinistra e quindi possiamo già disegnare la nostra circonferenza goniometrica. Questa volta però abbiamo a che fare con un coseno: perciò la retta che dobbiamo disegnare sarà adesso X= 0 che è una retta verticale!

La disequazione ci dice \cos x \ge 0 , ossia vuole i valori per il quale il coseno sia più grande di 0, quindi prendiamo tutti i valori che stanno dopo la retta ( a destra ). Inoltre mettiamo un puntino rosso agli estremi, visto che il simbolo di disuguaglianza contiene anche un uguale (\ge) e quindi vuole che comprendiamo gli estremi anche.

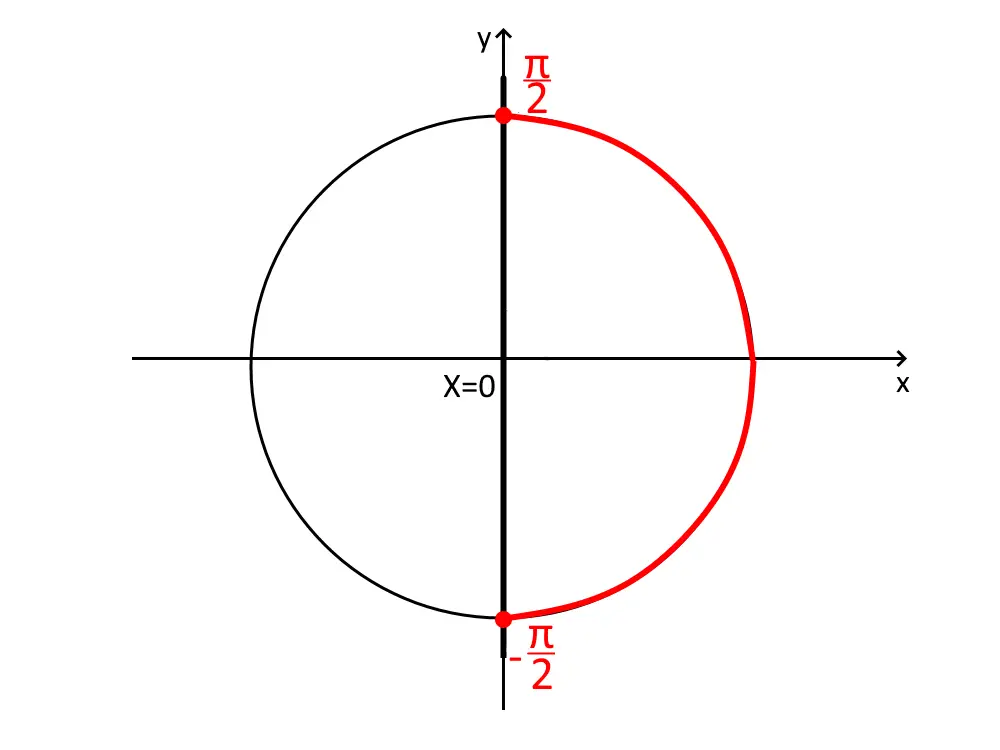
Qui non c’è bisogno della calcolatrice: notiamo facilmente che l’estremo sopra è \frac{\pi}{2}, mentre quello di sotto è lo stesso angolo ma cambiato di segno, quindi -\frac{\pi}{2}. Aggiungendo la periodicità, la soluzione è per cui:

-\frac{\pi}{2} + 2k \pi \le x \le \frac{\pi}{2} + 2k \pi

Continuiamo con altre disequazioni goniometriche esercizi svolti!

Esercizio 3. \tg x \le -1


Anche per la tangente non cambia il nostro discorso: seguiamo gli stessi punti detti per le equazioni goniometriche elementari. La tangente è già isolata, quindi disegniamo la circonferenza goniometrica. Visto che si tratta della tangente, disegniamo la retta tangente alla circonferenza, poi segniamo su tale retta il punto -1 ed evidenziamo tutta la parte inferiore. Inoltre segniamo con un punto rosso tale punto per ricordarci di prenderlo.

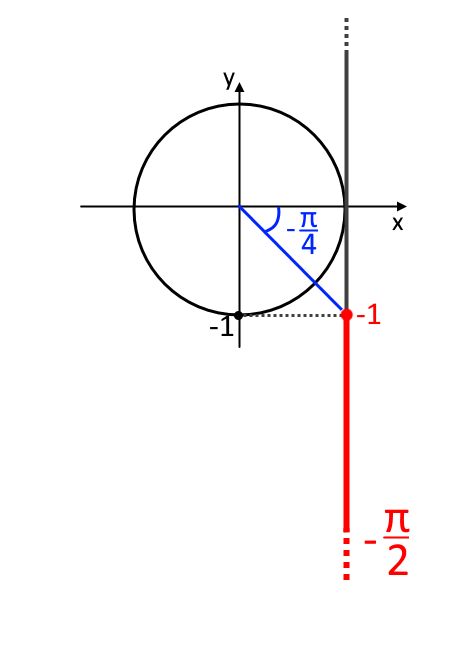
Vediamo sulla calcolatrice che l’angolo corrispondente alla \tg x= -1 è -\frac{\pi}{4} , e questo è il primo estremo. L’altro estremo dell’intervallo evidenziato va verso giù all’infinito, ed a tale infinito corrisponde l’angolo - \frac{\pi}{2} . Quindi l’intervallo di soluzione risulta essere:

- \frac{\pi}{2} \le x \le -\frac{\pi}{4}

A cui aggiungiamo la periodicità della tangente:

- \frac{\pi}{2} +k \pi \le x \le -\frac{\pi}{4} + k \pi


Chiaramente abbiamo messo - \frac{\pi}{2} =-90° a sinistra perché è più piccolo di - \frac{\pi}{4} =-45° !

Esercizio 4. \sin x \ge 1


Essa è una disequazione goniometrica elementare (c’è solo una funzione da sola), ed è già isolata. Disegniamo direttamente la circonferenza goniometrica, e qui notiamo un qualcosa di particolare. Tracciamo la retta orizzontale (essendo un seno) Y=1. La disequazione ci dice di prendere tutti i valori al di sopra o uguali ad 1. E quello che notiamo è che al di sopra non c’è nulla…ma come uguale ad 1 c’è un punto. Quindi l’unico punto soluzione è quello corrispondente al singolo angolo \frac{\pi}{2}, come vedete dal disegno.

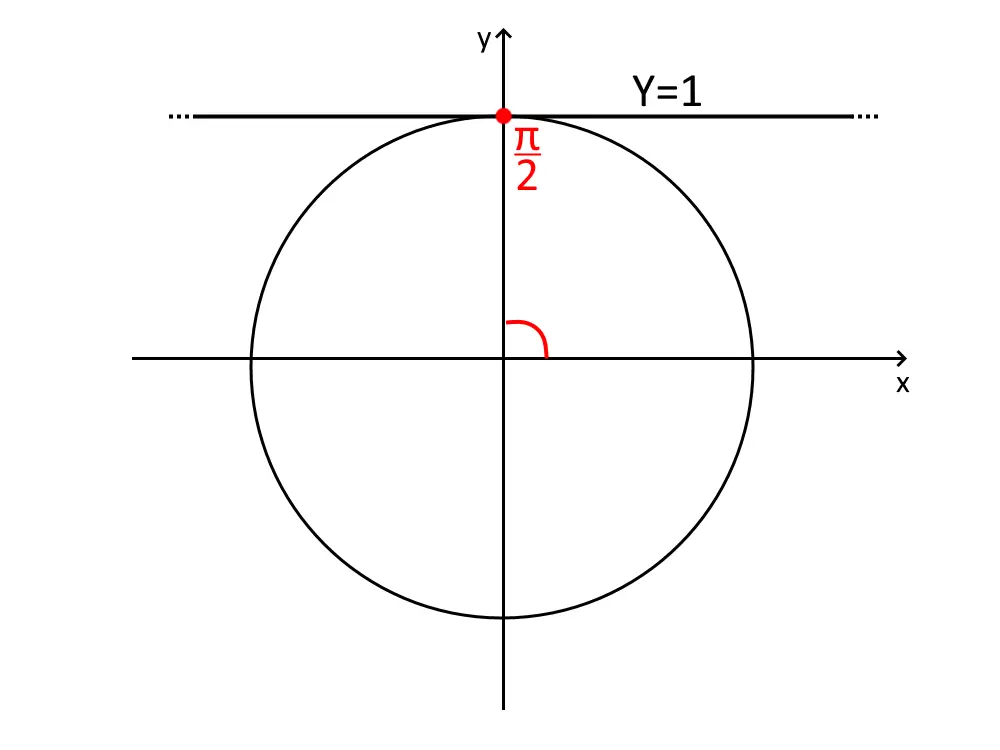
L’unica soluzione di questo esercizio è:

x= \frac{\pi}{2} +2k \pi

Esercizio 5. \cos x > \frac{1}{2} nell’intervallo [0,2\pi ]


Alcune volte il libro o il professore vi potrebbe dire di risolvere una disequazione goniometrica nell’intervallo di dominio della funzione in gioco. Per esempio qui abbiamo un coseno, e l’esercizio ci sta dicendo di trovare la soluzione solo in [0,2\pi ] . Questo significa che la soluzione non deve contenere la periodicità. Ed inoltre non deve contenere angoli negativi. Quindi gli intervalli soluzioni dovranno partire almeno dall’angolo 0, e finire al più con l’angolo 2 \pi !

Detto questo, seguiamo gli stessi punti degli altri esercizi. Il coseno è isolato: disegniamo la circonferenza goniometrica. Disegniamo la retta verticale X= \frac{1}{2} . La disequazione ci sta dicendo \cos x > \frac{1}{2} , ossia dobbiamo prendere tutti i valori del coseno più grandi di \frac{1}{2} ! Quindi evidenziamo l’arco di circonferenza che sta a destra della retta: quell’intervallo evidenziato col rosso è la nostra soluzione.

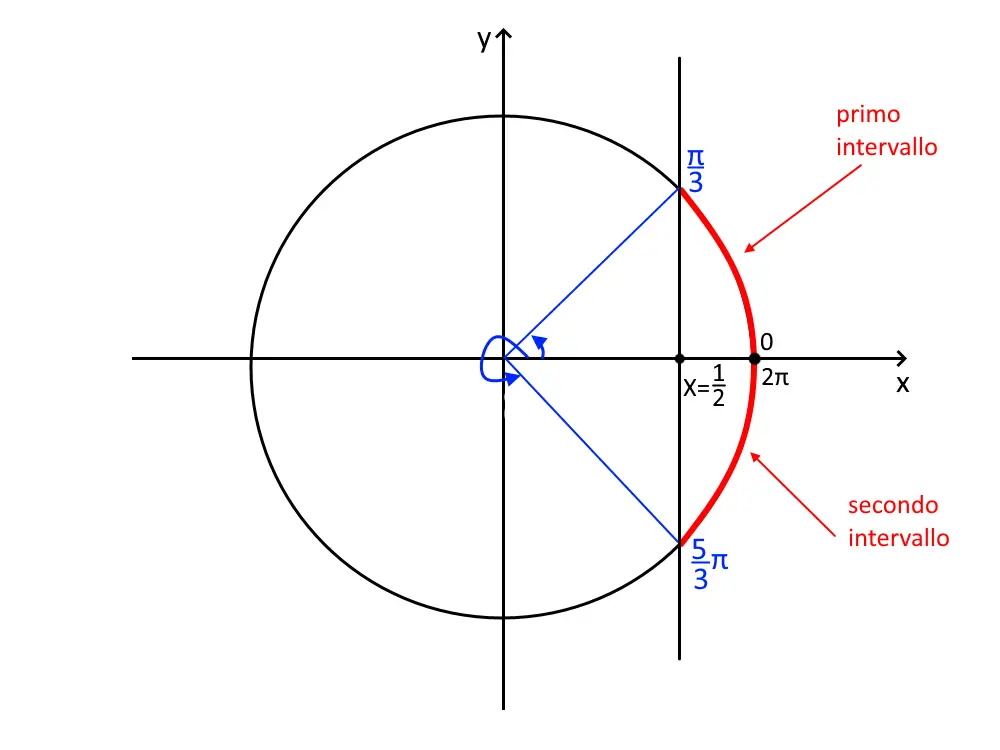
Per ciò detto prima, allora la soluzione parte dall’angolo 0 (che è l’angolo iniziale), poi procedendo in senso antiorario arriviamo ad un angolo per il quale il coseno è proprio \frac{1}{2} , e la calcolatrice ci dice che questo angolo è:

\frac{\pi}{3}

Quindi il primo intervallo di soluzione è:

0 < x < \frac{\pi}{3}

Ora andando avanti in senso antiorario incontriamo l’altro angolo che capiamo essere:

2\pi - \frac{\pi}{3} = \frac{5}{3} \pi

Fino ad arrivare all’estremo finale che è 2\pi. Questo secondo intervallo di soluzione è:

\frac{5}{3} \pi <x < 2\pi

E quindi la soluzione finale sarà:

0 < x < \frac{\pi}{3} \lor \frac{5}{3} \pi <x < 2\pi

Adesso vediamo esercizi svolti disequazioni goniometriche riconducibili a quelle elementari: ossia disequazioni che tramite trucchetti tipo mettere in evidenza ecc., si ritorna a disequazioni elementari.

Disequazioni goniometriche riconducibili a elementari

Come state vedendo stiamo seguendo gli stessi punti che abbiamo toccato per le equazioni goniometriche elementari ed equazioni goniometriche in generale. Di fatti quello che cambia è il ragionamento, ed il fatto che non si prendono più in generale singole soluzioni, ma intervalli di soluzioni. Adesso vediamo delle disequazioni che, con piccoli trucchetti, sono ricondubili a quelle elementari, viste nel capitolo appena fatto.

Esercizio 6. \cos^2 x - \cos x \ge 0


Questa è una disequazione che, tramite la messa in evidenza del \cos x , si ritorna ad una forma a noi familiare: quella di una disequazione goniometrica elementare. Di fatti mettendo in evidenza otteniamo:

\cos x ( \cos x - 1 ) \ge 0

Questa, essendo una disequazione con prodotto, la risolviamo tramite un falso sistema.


\big\| \cos x \ge 0 \\ \big\| \cos x - 1 \ge 0

E come vedete le due disequazioni che compaiono nel falso sistema le sappiamo risolvere singolarmente!

\big\| \cos x \ge 0 \\ \big\| \cos x \ge 1

Partiamo dalla seconda disequazione che è più semplice.

\cos x \ge 1

Di fatti disegniamo una circonferenza goniometrica, segniamo la retta verticale (essendo un coseno) X=1. La disequazione ci chiede di prendere i valori più grandi o uguali ad 1. Più grandi di 1 il coseno non ha valori, mentre uguale ad 1 ha un singolo angolo, che è:

x=0 + 2k\pi

E questa è la soluzione della seconda disequazione goniometrica elementare del falso sistema, ce la mettiamo dentro:

\big\| \cos x \ge 0 \\ \big\| 0+ 2k\pi

Ora dobbiamo risolvere la prima. Fate attenzione ad una cosa: quando ci sono falsi sistemi e quindi più soluzioni si vanno ad incrociare in un quadro dei segni, è assolutamente consigliato non mettere angoli negativi, almeno nella maggior parte dei casi.

Quindi pensiamo a risolvere:

\cos x \ge 0

Disegniamo la circonferenza goniometrica, la retta X=0, e prendiamo tutti i valori che sono più grandi di X=0, ossia sulla destra della retta.

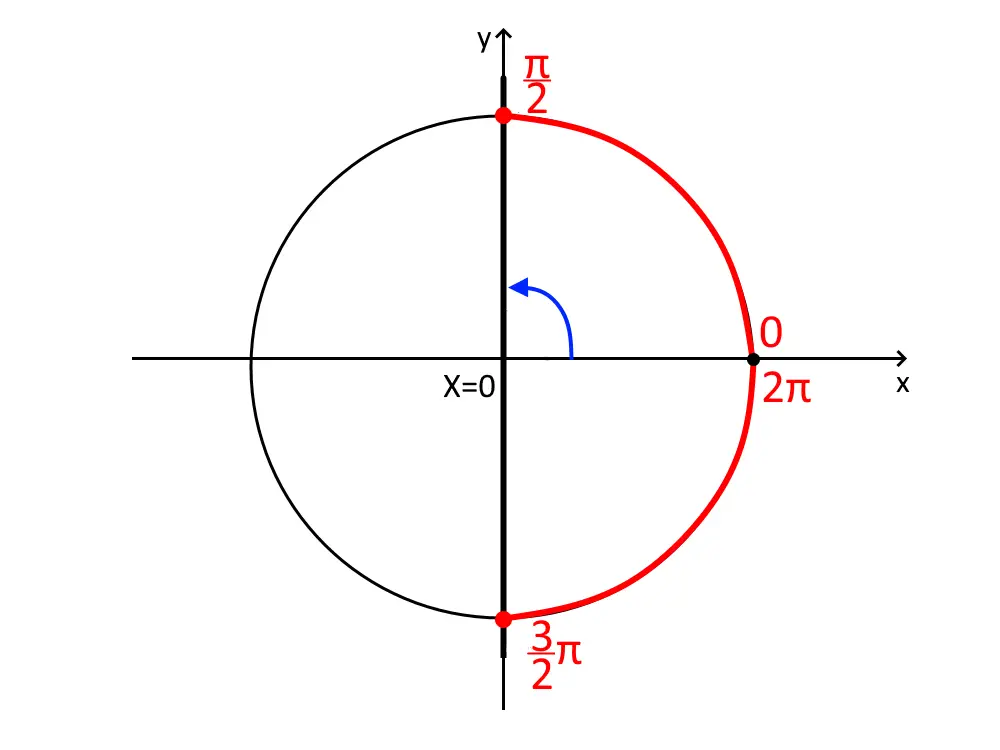
Non prendiamo gli angoli negativi, e quindi abbiamo come soluzione due intervalli di soluzioni separati che vanno da 0 fino a 2\pi, come visto nell’esercizio 5.

0 \le x \le \frac{\pi}{2} \lor \frac{3}{2}\pi \le x \le 2 \pi

Dove abbiamo messo \le perché la disequazione contiene una uguaglianza anche. Inoltre aggiungiamo la periodicità ed otteniamo:

2k\pi \le x \le \frac{\pi}{2} +2k\pi \lor \frac{3}{2}\pi +2k\pi \le x \le 2 \pi +2k\pi

Mettiamola a questo punto nel falso sistema:

\big\| 2k\pi \le x \le \frac{\pi}{2} +2k\pi \lor \frac{3}{2}\pi +2k\pi \le x \le 2 \pi +2k\pi \\ \big\| 0+2k\pi


Adesso disegniamo il quadro dei segni nell’intervallo [0,2\pi ] ! Ecco perché è consigliato non mettere angoli negativi, altrimenti poi non ci si capisce più nulla su quali intervalli si sovrappongono. Nel quadro dei segni non mettiamo la periodicità, la mettiamo alla fine nella soluzione!

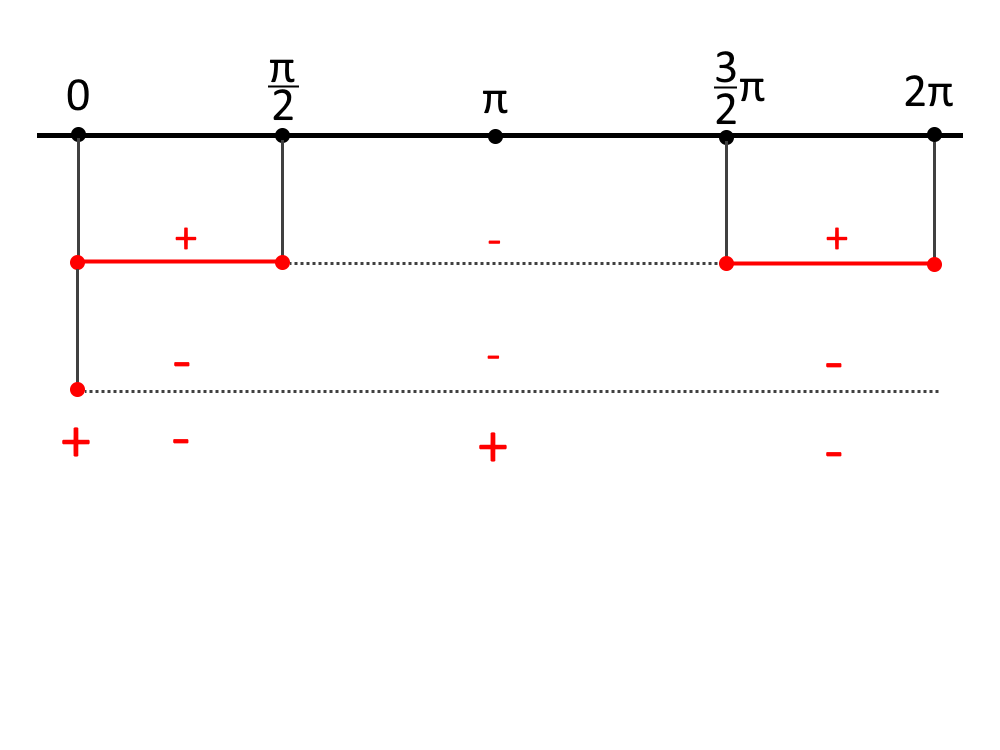
Questo era un quadro dei segni particolare, che può capitare sicuramente nella verifica: prendete nota!

La disequazione ci dice che dobbiamo prendere gli intervalli positivi, e quindi:

\frac{\pi}{2} \le x \le \frac{3}{2} \pi \land x=0

Aggiungendo la periodicità, otteniamo la soluzione finale dell’esercizio:

\frac{\pi}{2}+2k\pi \le x \le \frac{3}{2} \pi +2k\pi \land x=2k\pi

Continuiamo con altre disequazioni goniometriche esercizi svolti!

Esercizio 7. 2\sin^2 x + \sin x -1 < 0


Qui abbiamo una stessa funzione (seno) e poi abbiamo un quadrato del seno. Questo caso l’abbiamo già discusso per le equazioni goniometriche, e quando vedete una cosa del genere si procede per sostituzione. Poniamo:

\sin x = t

In questo modo la disequazione goniometrica diventa in termini di t:

2 t^2 + t -1 < 0

Ci siamo ricondotti a risolvere una disequazione di secondo grado, calcoliamone il delta:

\Delta = b^2 - 4ac = 1+8=9

Delta>0 in una disequazione con minore (<) allora dobbiamo prendere i valori interni delle singole soluzioni. Calcoliamole:

t_{1,2} = \frac{-b \pm \sqrt{\Delta} }{2a} = \frac{-1 \pm 3}{4}

Le singole soluzioni sono:

t_1 = \frac{-1+3}{4} = \frac{1}{2}

t_2 = \frac{-1-3}{4} = -1

Prendiamone i valori interni:

-1 < t < \frac{1}{2}

Abbiamo risolto la disequazione, ora dobbiamo ritornare alla x! Quindi risostituiamo:

-1 < \sin x < \frac{1}{2}

Quando vedete una cosa del genere, ossia una funzione al centro compresa fra due valori, si risolvono separatamente due disequazioni messe in un sistema:

\begin{cases} -1 < \sin x \\ \sin x < \frac{1}{2} \end{cases}

\begin{cases} \sin x > -1 \\ \sin x < \frac{1}{2} \end{cases}

Abbiamo due disequazioni goniometriche elementari da risolvere. Partiamo dalla prima:

\sin x > -1

Disegniamo la retta orizzontale Y=-1 e la circonferenza goniometrica. Dobbiamo prendere tutti i valori al di sopra di questa retta, e quindi…tutti tranne quello dove vale -1, e quindi dobbiamo solo escludere l’angolo \frac{3}{2}\pi .

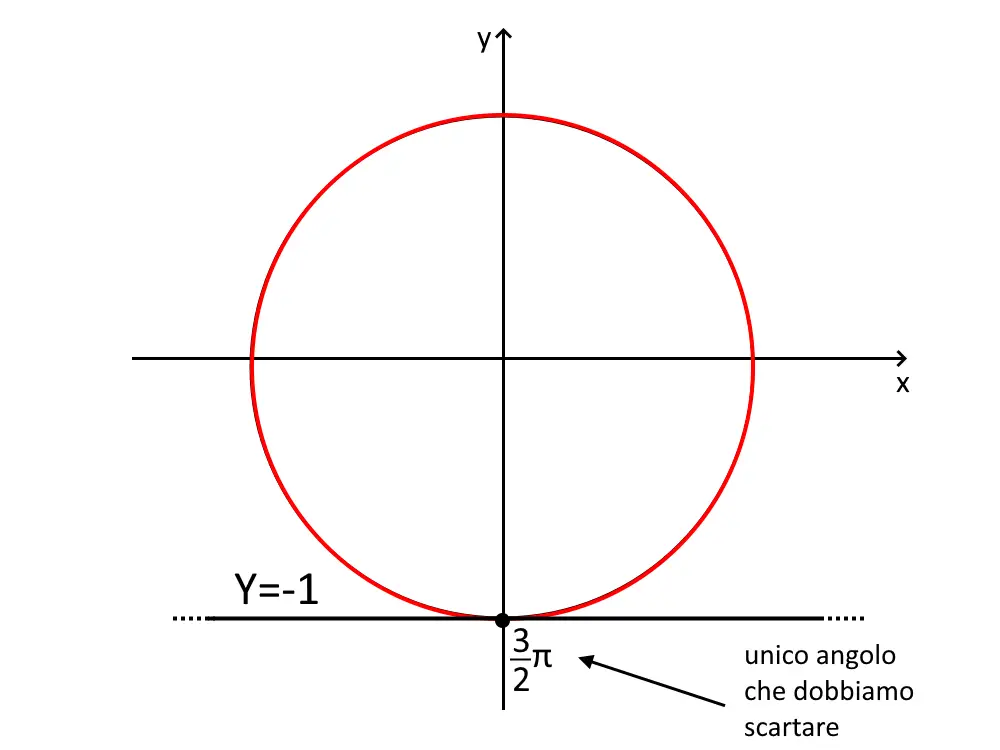
E quindi scriviamo x \ne \frac{3}{2}\pi

Risolviamo adesso la seconda:

\sin x < \frac{1}{2}

Disegniamo sempre la retta Y= \frac{1}{2} e la circonferenza goniometrica.

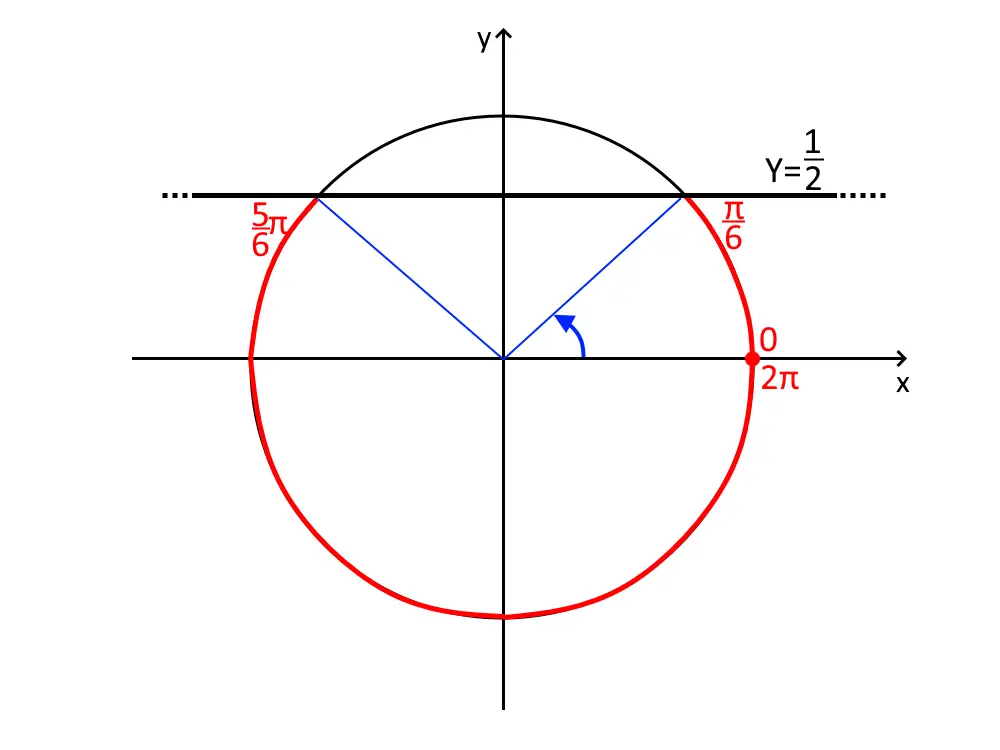
Il primo intervallo va da zero ad un angolo, cui il seno vale \frac{1}{2} e la calcolatrice ci dice che il primo angolo è 30°= \frac{\pi}{6}. Quindi:

0 \le x < \frac{\pi}{6}

Poi il secondo intervallo va da un certo angolo che notiamo essere \pi - \frac{\pi}{6}=\frac{5}{6}\pi , fino a 2\pi. Quindi:

\frac{5}{6}\pi < x \le 2 \pi

E di conseguenza la soluzione di questo primo termine di sistema è:

0 \le x < \frac{\pi}{6} \land \frac{5}{6}\pi < x \le 2 \pi

(alla fine aggiungiamo la periodicità)
Mettiamo tutto nel sistema:

\begin{cases}x \ne \frac{3}{2}\pi \\ 0 \le x < \frac{\pi}{6} \land \frac{5}{6}\pi < x \le 2 \pi \end{cases}

Nel sistema bisogna prendere gli intervalli comuni, e quindi, aggiungendo la periodicità, la soluzione dell’esercizio è:

2k\pi \le x < \frac{\pi}{6}+2k\pi \land \frac{5}{6}\pi +2k\pi< x \le 2 \pi +2k\pi \\ \land x \ne \frac{3}{2}\pi

Abbiamo visto due esercizi modello riguardante disequazioni goniometriche riconducibili a quelle elementari. Adesso vediamo esercizi svolti disequazioni goniometriche lineari.

Esercizi svolti disequazioni LINEARI

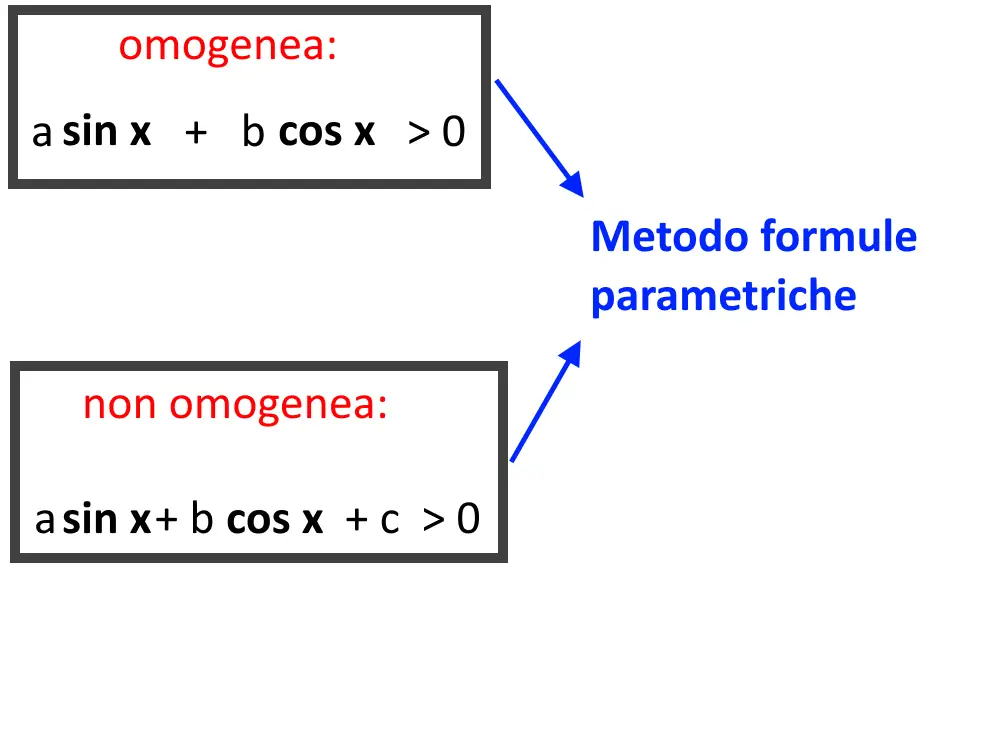
Esercizio 8. \sqrt{3} \sin x + \cos x \ge 0


(Armatevi di pazienza che sarà lunghetto)

Questa è una disequazione goniometrica lineare, cioè dove compare sia un seno che un coseno e basta. Inoltre rientriamo nel primo caso, quella omogenea, perché non ci sono altri numeri.

Questa invece è molto diversa dalle equazioni goniometriche lineari omogenee, perché se mentre nelle equazioni dividevamo per il coseno ora non possiamo farlo. Il metodo migliore in assoluto che vi consiglio è il metodo con le formule parametriche! Cioè sostituiamo il seno ed il coseno con:

\begin{cases} \sin x = \frac{2t}{1+t^2} \\ \cos x = \frac{1-t^2}{1+t^2} \end{cases}

Dove ricordiamo che t= \tg \frac{x}{2}

Sostituiamo, e la disequazione ora diventa:

\sqrt{3} \frac{2t}{1+t^2} + \frac{1-t^2}{1+t^2} \ge 0

Ci riconduciamo quindi alla risoluzione di una disequazione fratta. Facciamo per cui il minimo comune multiplo:

\frac{2 \sqrt{3} t +1-t^2 }{1+t^2} \ge 0

E la risolviamo come sempre scrivendo il suo falso sistema:

\big\| 2 \sqrt{3} t +1-t^2 \ge 0 \\ \big\| 1+t^2 >0

Ricordiamo che il segno uguale non ci va per la disequazione relativa al denominatore, per via delle CE, cioè che il denominatore non può essere uguale a zero.

Risolviamo una alla volta le due disequazioni, partiamo dal risolvere la seconda disequazione, che è la più semplice:

1+t^2 >0 \implies t^2 > -1

Un quadrato è per definizione non negativo, e quindi è sempre più grande di -1! Quindi:

\implies \forall t

Scriviamo tale risultato nel falso sistema.

\big\| 2 \sqrt{3} t +1-t^2 \ge 0 \\ \big\| \forall t

Adesso occupiamoci della prima disequazione del falso sistema:

2 \sqrt{3} t +1-t^2 \ge 0

Essa è una disequazione di secondo grado, e quindi riordiniamola prima cambiando di segno, perchè vogliamo il coefficiente a (cioè quello quadratico) positivo.

t^2 - 2 \sqrt{3} t - 1 \le 0

In una disequazione quando cambiate di segno tutto, ricordatevi di cambiare anche il segno stesso della disequazione (ora è diventato un minore).

Calcoliamo il delta:

\Delta = b^2 - 4ac = 12+4=16

Delta>0 in una disequazione col minore significa che esiste soluzione. La soluzione sarà i valori interni delle singole soluzioni seguenti:

t_{1,2} = \frac{-b \pm \sqrt{\Delta} }{2a} = \frac{ 2 \sqrt{3} \pm 4 }{2}

E quindi:

t_1 = \frac{ 2 \sqrt{3} + 4 }{2}= \sqrt{3} + 2

t_2 =\frac{ 2 \sqrt{3} - 4 }{2} = \sqrt{3} - 2

E quindi la soluzione in t è:

\sqrt{3} - 2 \le t \le \sqrt{3} + 2

Mettiamo finalmente questo risultato nel falso sistema iniziale:

\big\| \sqrt{3} - 2 \le t \le \sqrt{3} + 2 \\ \big\| \forall t

Prendiamo gli intervalli col segno + (essendo la disequazione col maggiore):

\sqrt{3} - 2 \le t \le \sqrt{3} + 2

Ora ritorniamo alla x, e quindi risostituiamo la t:

\sqrt{3} - 2 \le \tg \frac{x}{2} \le \sqrt{3} + 2

Anche questo si risolve scrivendo in un sistema i due pezzi separatamente:

\begin{cases} \tg \frac{x}{2} \le \sqrt{3} + 2 \\ \sqrt{3}- 2 \le \tg \frac{x}{2} \end{cases}

\begin{cases} \tg \frac{x}{2} \le \sqrt{3} + 2 \\ \tg \frac{x}{2} \ge \sqrt{3}-2 \end{cases}

Risolviamo queste due disequazioni goniometriche elementari una per volta, partiamo dalla prima.

\tg \frac{x}{2} \le \sqrt{3} + 2

Qui possiamo anche risparmiarci la sostituzione e scrivere direttamente. Disegniamo la circonferenza goniometrica, poi disegniamo la retta tangente, evidenziamo la parte in basso al punto \sqrt{3} + 2 e notiamo che l’intervallo di soluzione è:

- \frac{\pi}{2} < \frac{x}{2} \le 75°

Il valore di 75° ce lo dà la calcolatrice. Scriviamo 75° in radianti sfruttando la proporzione:

180° \; : \; \pi = 75° \; : \; \alpha

\implies \alpha = \frac{5}{12} \pi

Quindi questo primo intervallo del sistema è:

- \frac{\pi}{2} +k \pi < \frac{x}{2} \le \frac{5}{12} \pi + k\pi

Moltiplichiamo tutto per 2:

-\pi +2k \pi < x \le \frac{5}{6} \pi + 2k\pi

Scriviamolo nel sistema:

\begin{cases} -\pi +2k \pi < x \le \frac{5}{6} \pi + 2k\pi \\ \tg \frac{x}{2} \ge \sqrt{3}-2 \end{cases}

Ora risolviamo la seconda:

\tg \frac{x}{2} \ge \sqrt{3}-2

Stesso procedimento, e ricaviamo come secondo intervallo del sistema:

-\frac{\pi}{6} + 2k\pi \le x < \pi + 2k\pi

FINALMENTE possiamo concludere l’esercizio!

\begin{cases} -\pi +2k \pi < x \le \frac{5}{6} \pi + 2k\pi \\ -\frac{\pi}{6} + 2k\pi \le x < \pi + 2k\pi \end{cases}

Prendiamo l’intervallo comune, essendo un sistema.

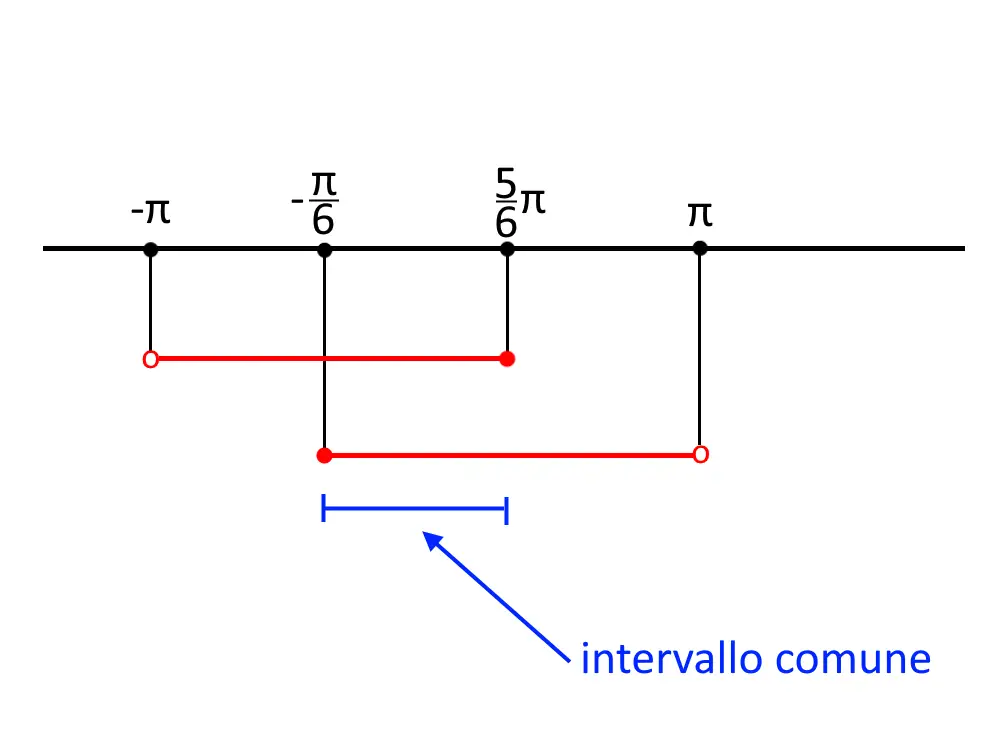
La soluzione finale dell’esercizio è:

- \frac{\pi}{6} +2k\pi \le x \le \frac{5}{6}\pi +2k\pi

Continuiamo con un altra disequazione goniometrica esercizi svolti!

Esercizio 9. \sin x - \cos x +1 \ge 0


Questo rientra nel caso non omogeneo invece: ma il procedimento è lo stesso. Sostituiamo quindi le funzioni seno e coseno con le formule parametriche ed otteniamo:

\frac{ 2t }{1+t^2} - \frac{1-t^2}{1+t^2} +1 \ge 0

E come prima ci riconduciamo quindi alla risoluzione dapprima di una disequazione fratta. Facciamo il mcm allora:

\frac{ 2t - (1-t^2) + (1+t^2) }{1+t^2} \ge 0

\frac{ 2t^2 +2t }{1+t^2} \ge 0

Mettiamo in evidenza 2t:

\frac{ 2t(t+1) }{1+t^2} \ge 0

Lo risolviamo con un falso sistema:

\big\| 2t(t+1) \ge 0 \\ \big\| 1+t^2 >0

\big\| 2t(t+1) \ge 0 \\ \big\| t^2 > -1

Partiamo dal secondo che è più semplice, inoltre è lo stesso ragionamento fatto prima: cioè essendo un quadrato definito non negativo è certamente sempre più grande di -1, quindi scriviamo come segue.

\big\| 2t(t+1) \ge 0 \\ \big\| \forall t

Il primo è una disequazione con prodotto, e la risolviamo un attimo da parte con un altro falso sistema:

\big\| 2t \ge 0 \\ \big\| t+1 \ge 0

\big\| t \ge 0 \\ \big\| t \ge -1

Prendiamo gli intervalli positivi, ossia:

t \le -1 \lor t \ge 0

Sostituiamo questo risultato nel falso sistema iniziale:

\big\| t \le -1 \lor t \ge 0 \\ \big\| \forall t

Anche su questo dobbiamo prendere gli intervalli col segno +, cioè:

t \le -1 \lor t \ge 0

Adesso che abbiamo trovato la t, è il momento di ritornare alla x!

\tg \frac{x}{2} \le -1 \lor \tg \frac{x}{2} \ge 0

Risolviamo queste due immediate disequazioni goniometriche una per volta, partiamo dalla prima!

\tg \frac{x}{2} \le -1

Disegnando la circonferenza goniometrica ed evidenziando i valori più piccoli di -1 otteniamo un’intervallo di angoli:

- \frac{\pi}{2} +k \pi < \frac{x}{2} \le - \frac{\pi}{4} + k \pi

Moltiplichiamo per 2 tutto ed abbiamo la prima soluzione:

- \pi +2k \pi < x \le - \frac{\pi}{2} + 2k \pi

Passiamo all’altra disequazione elementare:

\tg \frac{x}{2} \ge 0

E questa facilmente è risolvibile ottenendo come soluzione:

0 +k \pi < \frac{x}{2} < \frac{\pi}{2} + k \pi

Moltiplichiamo tutto per 2:

0+2k \pi < x < \pi + 2k \pi

E quindi la soluzione finale dell’esercizio è:

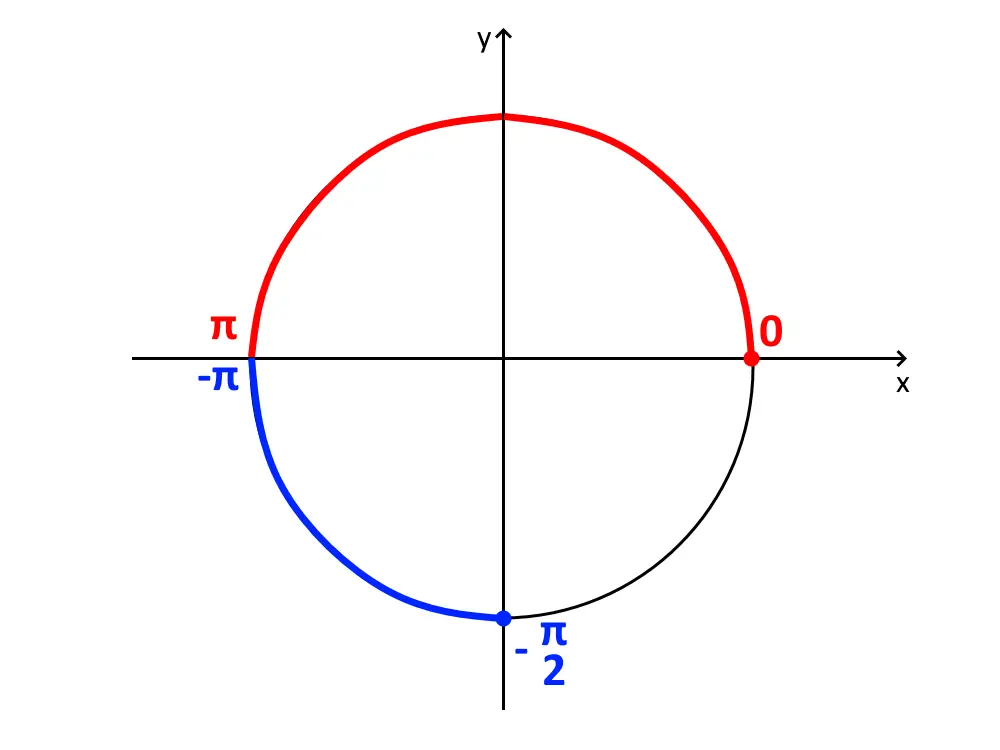
- \pi +2k \pi < x \le - \frac{\pi}{2} + 2k \pi \lor 0+2k \pi < x < \pi + 2k \pi

Visto che il simbolo \lor significa unione, dobbiamo unire le due soluzioni, ed otteniamo una unica seguente:

2k \pi \le x \le \frac{3}{2}\pi + 2k \pi

In questa pagina concludiamo la parte di equazioni/disequazioni goniometriche. Se volete dare una ripassata prima della verifica potete trovare esercizi svolti anche su identità goniometriche, equazioni goniometriche elementari ed equazioni goniometriche!

Trovate altre centinaia di esercizi svolti sul nostro sito sia di matematica che altro ancora!



Per approfondire:
https://it.wikipedia.org/wiki/Disequazione_trigonometrica


Disequazioni goniometriche esercizi svolti

Disequazioni
goniometriche
esercizi

Numeri
complessi
esercizi