Studio di una funzione
Studio di una funzione: esercizi SVOLTI! Lo studio di una funzione è argomento dello scritto d’esame di stato e della verifica in classe. Lo studio di una funzione racchiude i seguenti argomenti in ordine: dominio, ricerca di simmetrie, intersezioni con gli assi, positività, studio degli estremi (e quindi ricerca asintoti), massimi e minimi, concavità. In questa pagina vedremo come svolgere lo studio di una funzione per tutte le funzioni che possono capitare!
Indice
- Studio di una funzione: passaggi
- Studio funzione polinomiale
- Studio funzione fratta
- Studio funzione con radice
- Studio funzione esponenziale
- Studio funzioni logaritmiche
- Studio funzioni goniometriche
- Studio funzione partendo dal grafico
Partiamo subito col vedere tutti i passaggi principali che seguiremo per ogni esercizio sullo studio delle funzioni!
Studio di una funzione PASSAGGI

Applichiamo questi passaggi ad un primo esercizio: sulla funzione polinomiale!
Studio funzione POLINOMIALE
Esercizio 1. y= x^2 - x^3
Primo punto: dominio. Per una funzione polinomiale non ci sono problemi di dominio, essa è definita in tutto l’asse x:
D: x \in \Reals
Quindi non dobbiamo cancellare nessuna parte del grafico, perché in tutto l’asse esso è presente!
Secondo punto: ricerca eventuali simmetrie. Dobbiamo verificare cioè se la funzione è pari o dispari, per far ciò verifichiamo che se:
Pari: f(-x)= f(x)
Dispari: f(-x)=- f(x)
Quindi andiamo semplicemente a sostituire al posto della x, una -x. Ossia con segno meno.
y= (-x)^2 - (-x)^3
\implies y= x^2 + x^3
Come possiamo vedere otteniamo una funzione che non è la stessa di partenza, né con tutti i segni opposti: quindi non è né pari né dispari, andiamo avanti!
Terzo punto: intersezioni con gli assi. In realtà ci concentriamo solo sull’intersezione con l’asse y, perché quelle con l’asse x le si deducono direttamente con lo studio del segno (prossimo punto). Per vedere dove la funzione interseca l’asse y, bisogna imporre che x=0, e così ci troveremo la y:
y= 0^2 - 0^3 = 0
Quindi la funzione taglia l’asse y nel punto (0,0). E ci disegniamo un punto sul grafico, per ricordarci che la funzione deve passare da questo punto!
Quarto punto: studio del segno. Andiamo a studiarne il segno! Se non vi ricordate come si studia il segno di una funzione, o come si calcola il dominio ecc. vi consiglio assolutamente prima di andarvi a vedere uno per uno ogni capitolo!
Poniamo quindi la funzione maggiore o uguale di zero:
x^2 - x^3 \ge 0
Notiamo che possiamo mettere in evidenza una x^2:
x^2 (1 - x ) \ge 0
Questo è un prodotto in una disequazione, e di conseguenza dobbiamo risolvere un falso sistema:
\big\| x^2 \ge 0 \\ \big\| 1-x \ge 0
Il primo pezzo è un quadrato e di conseguenza sempre positivo o uguale a zero per definizione.
\big\| \forall x \\ \big\| -x \ge -1
\big\| \forall x \\ \big\| x \le 1
Disegnando il suo schema dei segni, e prendendo l’intervallo col segno +, si ha:
x \le 1
Questo significa che è in questo intervallo che la soluzione è positiva, ossia sta al di sopra. Quindi cancelliamo il resto come segue. (Ricordatevi che ad ogni passaggio, se necessario, bisogna andare ad inserire le informazioni nel grafico.)
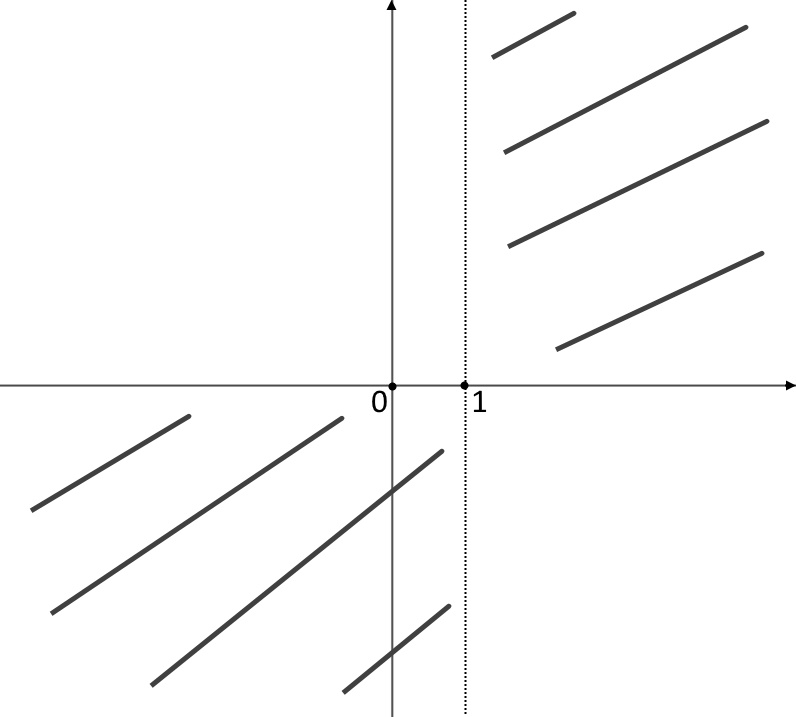
Quinto punto: studio estremi ed eventuale ricerca di asintoti. La funzione è definita sia in + infinito, che in -infinito. Quindi possiamo andare a studiarne gli estremi, facendone i limiti:
\lim\limits_{+ \infin } x^2 - x^3 = + \infin - \infin
Notiamo che è una forma indeterminata, quindi per eliminarla mettiamo in evidenza come segue:
\lim\limits_{+ \infin } x^2 (1 - x) = + \infin (1- \infin ) = +\infin \cdotp (- \infin ) = -\infin
Ciò significa che verso destra la funzione va verso giù nel grafico. Dopo lo disegneremo. Ora studiamo un attimo l’altro estremo:
\lim\limits_{- \infin } x^2 (1 - x) = + \infin (1+ \infin ) = +\infin \cdotp (+ \infin ) = +\infin
Qui invece verso sinistra, la funzione va verso l’alto. Ora è necessario verificare l’esistenza degli asintoti: qui abbiamo dei limiti solamente che vanno ad infinito, e di conseguenza potrebbero esistere SOLO asintoti obliqui. Dobbiamo verificare che esiste finito:
m= \lim\limits_{+ \infin } \frac{x^2 (1 - x)}{x} = \lim\limits_{+ \infin } x (1 - x) = -\infin
E quindi non esiste finito. L’altro è la stessa cosa. Non ci sono gli asintoti, quindi andiamo solo a disegnare sul grafico cosa fa la funzione agli estremi.
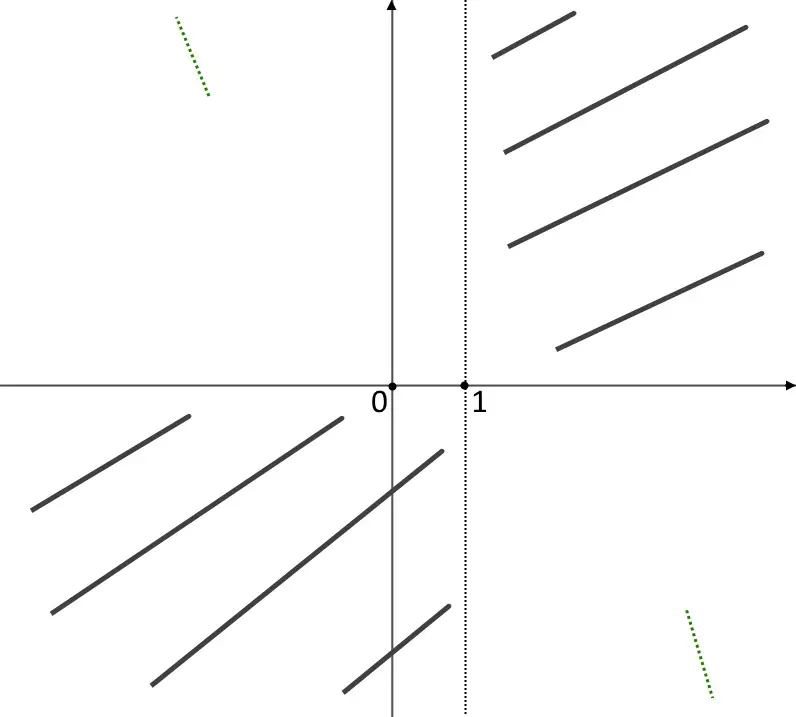
Sesto punto: massimi e minimi. Andiamo quindi a fare la derivata e trovare eventuali massimi e minimi.
y'= 2x - 3x^2
Scriviamo il dominio della derivata, per vedere se è lo stesso: se non lo è potrebbero esserci punti di cuspide, angolosi ecc. (punti di non derivabilità).
Notiamo che è sempre un polinomio, e quindi il dominio della derivata è lo stesso della funzione. Andiamo avanti.
2x - 3x^2 > 0
Mettiamo in evidenza una x:
x(2 - 3x) > 0
E risolviamo il suo falso sistema:
\big\| x>0 \\ \big\| 2-3x > 0
\big\| x>0 \\ \big\| x < \frac{2}{3}
Facciamo lo schema dei massimi e minimi con i segni corrispondenti (se non vi ricordate come si disegna cliccateci sopra):
Quindi il punto x=\frac{2}{3} è un punto di massimo relativo, a cui corrisponde:
y= (\frac{2}{3})^2 - (\frac{2}{3})^3 = \frac{4}{9} - \frac{8}{27} = \frac{4}{27}
Quindi il punto di massimo che dopo disegneremo è: (\frac{2}{3},\frac{4}{27})
Invece x=0 è un punto di minimo relativo, cui corrisponde una y:
y= 0^2 - 0^3 =0
Quindi il punto di minimo è (0,0). Disegniamoli sul grafico.
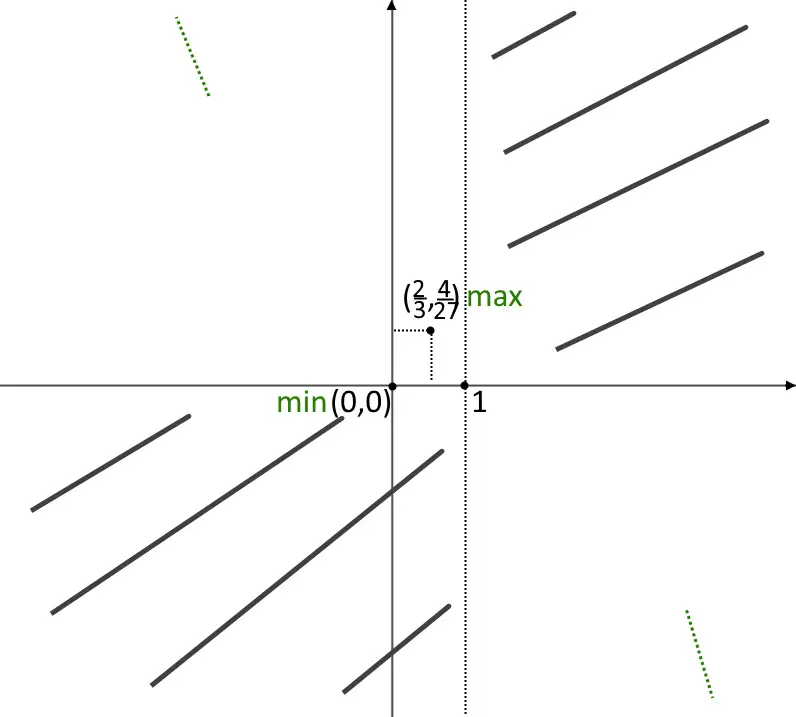
Settimo punto: studio concavità. Facciamone la derivata seconda e vediamo se la funzione è concava o convessa. Sappiamo che:
y'= 2x - 3x^2
y''= 2 - 6x > 0
Quindi:
- 6x > -2
x < \frac{1}{3}
Disegniamo il suo schema relativo alla concavità. Se non vi ricordate cliccateci un attimo sopra.
E di conseguenza la funzione si comporta in questo modo in tali intervalli: in x < \frac{1}{3} ha una concavità verso l’alto, nell’altro verso il basso. Quindi nel punto x = \frac{1}{3} cambia concavità, segniamocelo. Disegniamo a questo punto la funzione, tenendo conto di questa concavità. L’esercizio sullo studio di una funzione polinomiale è concluso!
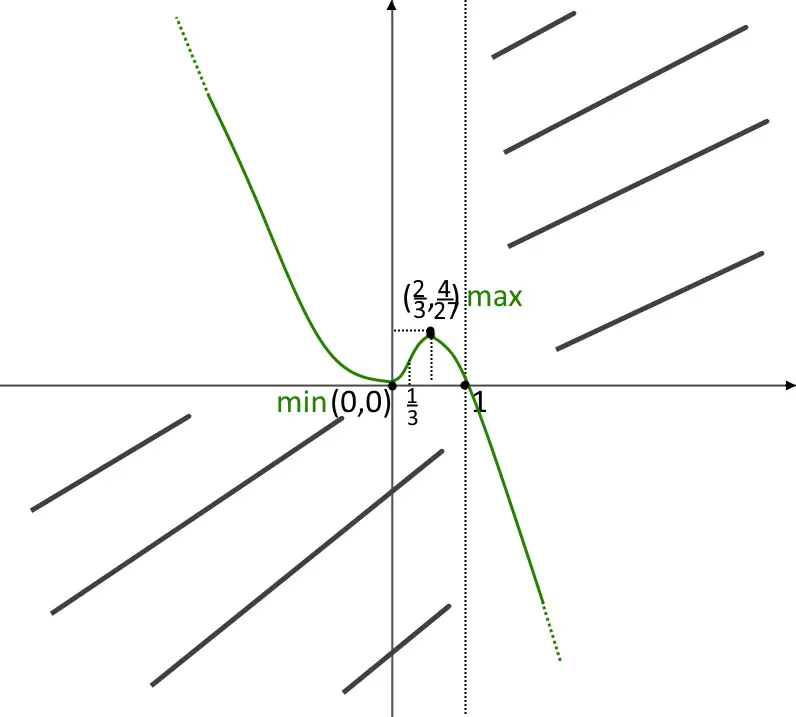
Vediamo come comportarci con una funzione fratta!
Studio funzione FRATTA
Esercizio 2. y= \frac{x^2}{x^2 +1 }
Primo punto: dominio. Per una funzione fratta significa porre il denominatore diverso da zero.
D: x^2 +1 \ne 0 \implies x^2 \ne -1
Un quadrato non è mai negativo, tantomeno pari a -1, quindi anche questa funzione è definita in tutto l’asse R.
D: x \in \Reals
Secondo punto: ricerca simmetrie. Scambiamo al posto della x una -x, e vediamo cosa esce fuori, e se possiamo ricondurci alle due relazioni scritte nell’esercizio precedente.
y= \frac{(-x)^2}{(-x)^2 +1 }
E viene:
y= \frac{x^2}{x^2 +1 }
Ossia esattamente la stessa funzione di partenza, quindi abbiamo scoperto che f(-x)=f(x) cioè la funzione è pari.
Cosa fare quando c’è una simmetria? Visto che c’è simmetria, considereremo solamente la parte destra del grafico, quindi l’intervallo x \ge 0 e studieremo solo questa! Alla fine disegneremo il grafico anche a sinistra semplicemente specchiando quello di destra. Cioè ci stiamo semplificando la vita! Ora vedrete meglio tutto!
(Qui non dovete cancellare la parte sinistra, ci servirà alla fine come detto)
Terzo punto: intersezione assi. Come detto prima, ci interessiamo solo all’intersezione con asse y, imponiamo quindi che x=0:
y= \frac{0^2}{0^2 +1 } =0
La funzione passa quindi in tale punto (0,0), segniamocelo!
Quarto punto: studio del segno. Quindi vediamo in pratica dove la funzione sta sotto e dove sta sopra, e dove interseca gli assi.
\frac{x^2}{x^2 +1 } \ge 0
Questa è una disequazione fratta, che quindi risolviamo con un falso sistema:
\big\| x^2 \ge 0 \\ \big\| x^2 +1 > 0
(ricordate che il denominatore non può essere uguale a zero)
\big\| x^2 \ge 0 \\ \big\| x^2 > -1
\big\| \forall x \\ \big\| \forall x
Con lo schema dei segni, notiamo facilmente, che in tutto R c’è un segno +, e quindi in tutto R la funzione è positiva (sta sopra). Cancelliamo quindi la parte sotto che non ci interessa.
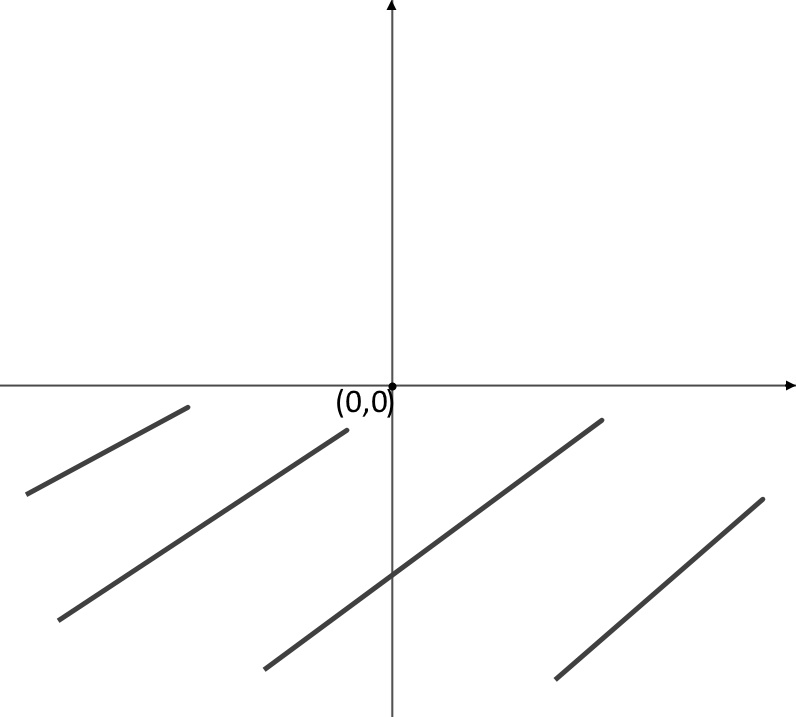
Quinto punto: estremi ed eventuali asintoti. Visto che la funzione agli estremi è definita, possiamo studiarli.
\lim\limits_{+ \infin } \frac{x^2}{x^2 +1 } = \lim\limits_{+ \infin } \frac{x^2}{x^2 (1+\frac{1}{x^2}) } =1
Abbiamo messo in evidenza il grado più alto perché è una forma indeterminata infinito diviso infinito. Il limite va ad 1, questo significa che è un asintoto orizzontale, ossia la funzione tende ad andare come la retta y=1. L’altro non ha senso calcolarlo, perché sarà lo stesso, visto che la funzione è pari.
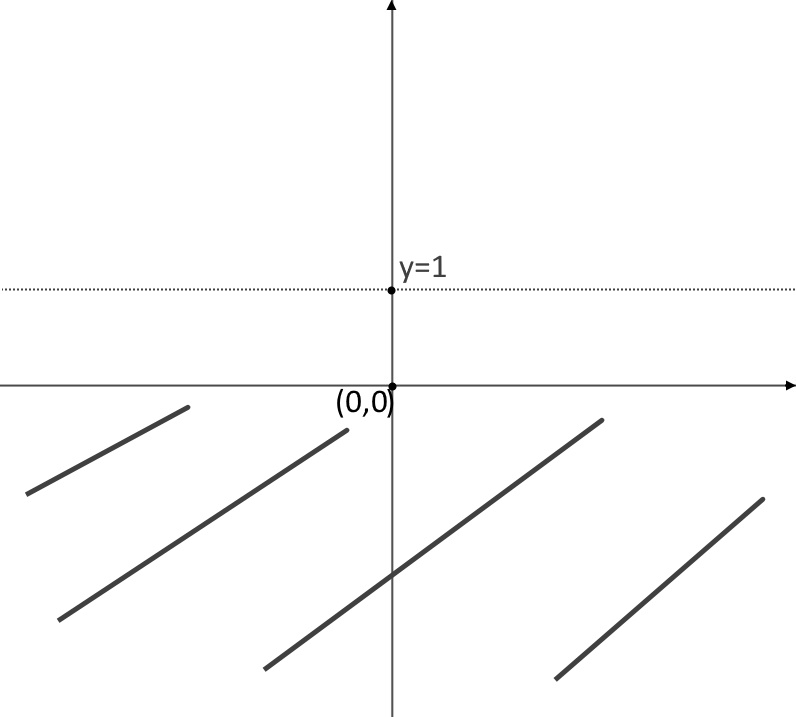
Sesto punto: massimi e minimi. Facciamone la derivata e vediamo i punti di massimo e minimo relativi della funzione.
y'= \frac{2x (x^2 +1 ) -x^2 \cdotp 2x }{(x^2 +1)^2 }
Il dominio della derivata notiamo che è lo stesso della funzione, andiamo avanti.
y'= \frac{ 2x }{(x^2 +1)^2 } > 0
Abbiamo come spesso capita, una disequazione fratta, e quindi falso sistema.
\big\| 2x > 0 \\ \big\| (x^2 +1)^2 > 0
Nel secondo pezzo abbiamo un quadrato definito non negativo, quindi sicuramente >0, ed allora:
\big\| x > 0 \\ \big\| \forall x
Nel quadro dei segni dobbiamo prendere l’intervallo positivo, ossia x>0. Questo è il falso sistema relativo alla ricerca dei massimi e minimi relativi, notiamo quindi che, come fatto nell’esercizio precedente:
x=0 è un punto di minimo relativo quindi, cui corrisponde una:
y= \frac{0^2}{0^2 +1 } = 0
Disegniamo il punto (0,0) come punto di minimo sul grafico.
Settimo punto: concavità. Studiamo la derivata seconda ed il comportamento della funzione. Riprendiamo da:
y'= \frac{ 2x }{(x^2 +1)^2 }
Facciamo la derivata seconda:
y''= \frac{ 2(x^2 +1)^2 - 2x \cdotp 2(x^2+1)2x }{(x^2 +1)^4 }
\frac{ -6x^4 -4x^2 +2 }{(x^2 +1)^4 } >0
Scriviamo il suo falso sistema: (il calcolo della concavità spesso è molto lungo per le funzioni fratte…)
\big\| -6x^4 -4x^2 +2 > 0 \\ \big\| (x^2 +1)^4 > 0
Il secondo pezzo è verificato sempre, essendo che dentro c’è roba positiva, ed è alla quarta. Il primo è riconducibile ad una disequazione di secondo grado, ponendo x^2 = t , cambiamo inoltre di segno:
\big\| 6t^2 +4 -2 < 0 \\ \big\| \forall x
\frac{\Delta}{4} = (\frac{b}{2})^2 -ac = 4+12=16
Poi le singole soluzioni, ed infine ne prendiamo i valori interni, essendoci un minore:
t_{1,2}= \frac{- \frac{b}{2} \pm \sqrt{ \frac{\Delta}{4} } }{a} = \frac{-2 \pm 4}{6}
Ossia, prendendone i valori interni:
-1<t< \frac{1}{3}
Risostituiamo:
-1<x^2< \frac{1}{3}
Quando avete una cosa del genere, bisogna scrivere un sistema e prendere i valori in comune:
\begin{cases} x^2 > -1 \\ x^2 < \frac{1}{3} \end{cases}
\begin{cases} \forall x \\ -\frac{1}{\sqrt{3}} < x < \frac{1}{\sqrt{3}} \end{cases}
E quindi la soluzione del sistema è:
-\frac{1}{\sqrt{3}} < x < \frac{1}{\sqrt{3}}
Sostituiamo finalmente nel falso sistema della concavità e concludiamo l’esercizio:
\big\| -\frac{1}{\sqrt{3}} < x < \frac{1}{\sqrt{3}} \\ \big\| \forall x
Quindi nell’intervallo -\frac{1}{\sqrt{3}} < x < \frac{1}{\sqrt{3}} ha concavità positiva, ossia verso l’alto, e negli altri due intervalli verso il basso. Disegniamo il grafico.
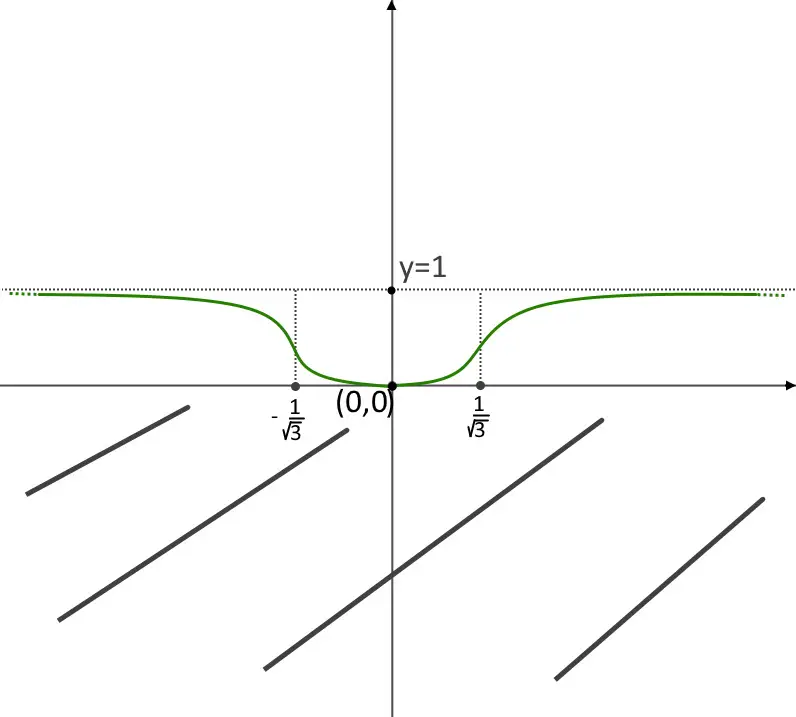
Continuiamo con altri esercizi svolti sullo studio di una funzione radice!
Studio funzione con RADICE
Esercizio 3. y= \sqrt{x^2 - 4}
Primo punto: dominio. Il dominio di una funzione radice (con esponente pari) è radicando (quello che sta dentro) maggiore o uguale a zero, come segue.
D: x^2 -4 \ge 0 \implies x^2 \ge 4
D: x \le -2 \land x \ge 2
Quindi la funzione risiede ed esiste in tali intervalli, cancelliamo perciò il restante.
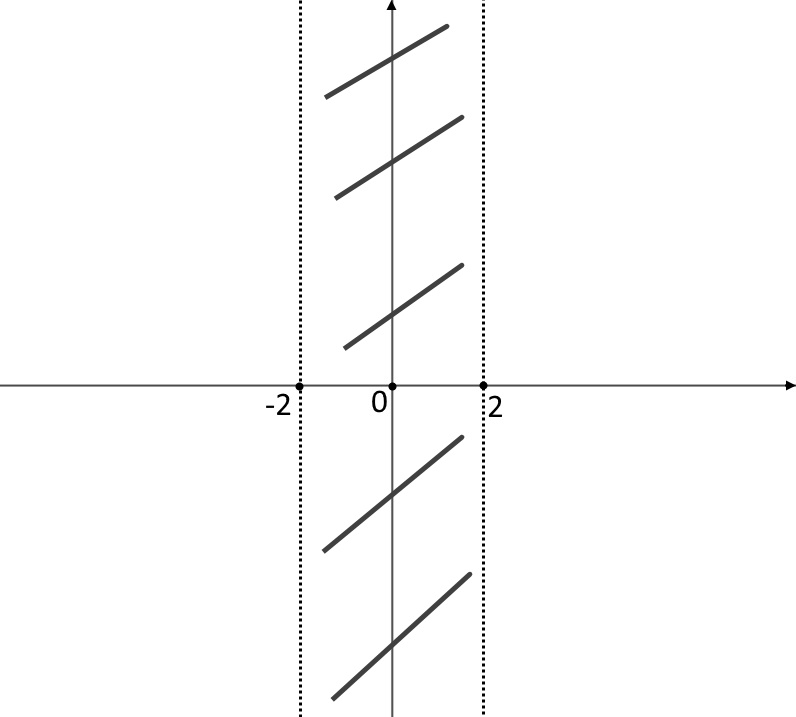
Secondo punto: ricerca simmetrie. Sostituiamo come sempre la -x nella funzione, al posto della x, e vediamo cosa esce fuori:
y= \sqrt{(-x)^2 - 4} = \sqrt{x^2 - 4}
Cioè ci dà la stessa funzione di partenza, ossia f(-x)=f(x), ossia è pari. Come prima quindi, concentriamoci solo sullo studiare la parte destra del grafico, e poi disegneremo quella sinistra capovolgendo simmetricamente la parte di destra.
Terzo punto: intersezione assi. Dovremmo imporre che x=0, ma non fa parte del dominio, quindi ovviamente la funzione non interseca l’asse y, anche perché l’abbiamo cancellato dal grafico!
Quarto punto: studio segno. Vediamo dove la funzione sta sotto e dove sta sopra, e dove interseca l’asse x quindi:
y= \sqrt{x^2 - 4} \ge 0
Una radice, nel suo dominio, è sempre positiva o uguale a zero. Una radice non può essere negativa, e quindi ciò è vero sempre nel proprio dominio, ossia in:
x \le -2 \land x \ge 2
Ossia, la funzione sta sempre sopra, nel suo dominio chiaramente. Notiamo anche che nei punti x=-2, x=2 tocca l’asse x. Cancelliamo la parte di sotto.
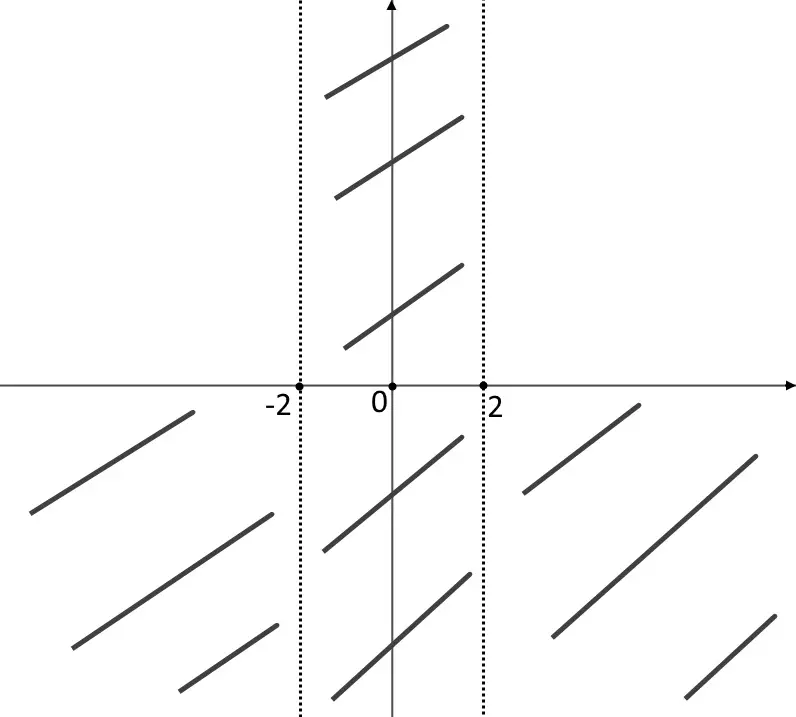
Quinto punto: studio estremi e asintoti. La funzione è definita agli estremi e quindi li possiamo studiare. Studiamo solo l’estremo destro, perché la funzione è pari e quindi il risultato dell’estremo sinistro sarebbe lo stesso, per via della simmetria.
\lim\limits_{+ \infin } \sqrt{x^2 - 4} = + \infin
La funzione tende ad andare su, verso destra. Controlliamo se c’è un asintoto obliquo, verifichiamo che esista:
m= \lim\limits_{+ \infin } \frac{ \sqrt{x^2 - 4} }{x} = \lim\limits_{+ \infin } \sqrt{ \frac{ x^2 - 4 }{x^2} }=
= \lim\limits_{+ \infin } \sqrt{ \frac{ x^2 (1- \frac{4}{x^2}) }{x^2} } = 1
Quindi dovrebbe esistere l’asintoto obliquo. Calcoliamo ora il coefficiente noto:
q = \lim\limits_{+ \infin } ( \sqrt{x^2 - 4} - x) = \lim\limits_{+ \infin } ( \sqrt{x^2 - 4} - x) \frac{( \sqrt{x^2 + 4} - x)}{( \sqrt{x^2 + 4} - x)} =
Questa è una forma indeterminata con radice, cliccateci sopra se non vi ricordate, in questo modo eliminiamo la forma indeterminata infinito – infinito.
= \lim\limits_{+ \infin } \frac{ x^2 + 4 - x^2 }{ \sqrt{x^2 + 4} + x} = \lim\limits_{+ \infin } \frac{ 4}{ \sqrt{x^2 + 4} + x} = 0
Quindi l’asintoto obliquo, per la quale la funzione va a tendere, è la retta y=x.
(vista la simmetria, l’altra retta sarà y=-x! )
Disegniamo perciò le due rette tratteggiate.
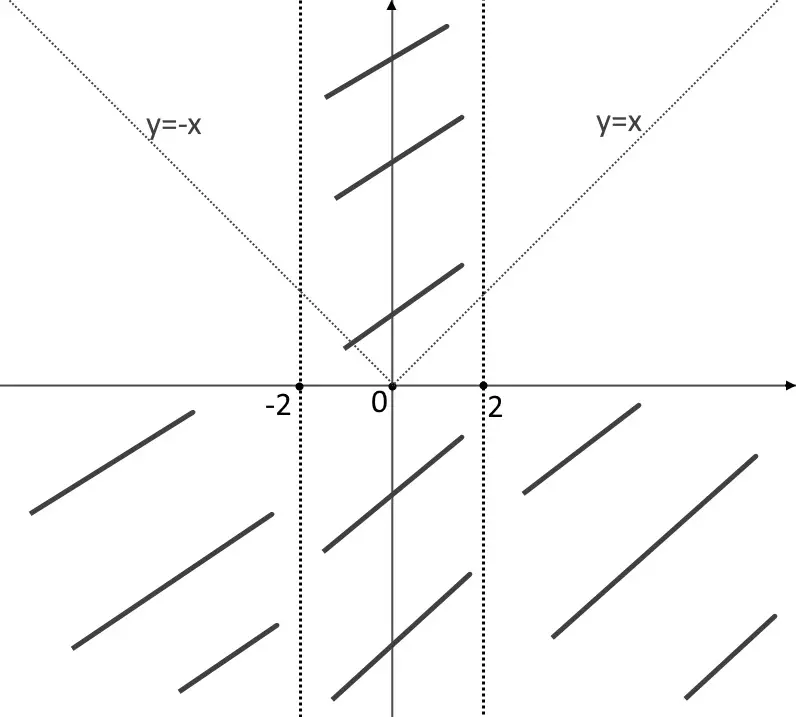
Sesto punto: massimi e minimi.
y'= \frac{2x}{2\sqrt{x^2 - 4} }
Scriviamo il dominio della derivata:
D’: x^2 -4 \ne 0 \implies x \ne \pm 2
Quindi notiamo che ci sono due punti di non derivabilità, li andremo a studiare dopo.
\frac{x}{ \sqrt{x^2 - 4} } > 0
Risolviamolo con un falso sistema.
\big\| x > 0 \\ \big\| \sqrt{x^2 - 4} > 0
La radice è sempre maggiore o uguale a zero. Di conseguenza essa è sempre >0, tranne nei punti in cui essa è uguale a zero, ossia:
\big\| x > 0 \\ \big\| x^2 - 4 \ne 0
\big\| x > 0 \\ \big\| x \ne \pm 2
Disegniamo lo schema dei segni inserendoci anche il dominio chiaramente. Come possiamo vedere i punti di minimo sono due:
x=\pm 2
Concentriamoci solo su x=2, perchè ci interessiamo della parte destra per il momento.
Vediamo che valore di y ha la funzione nel punto x=2.
y= \sqrt{2^2 - 4} = 0
Quindi il punto (2,0) è di minimo!
Per simmetria quindi anche (-2,0), perché la funzione assumerà lo stesso uguale valore di y=0 anche a sinistra.
Adesso dobbiamo studiare i punti di non derivabilità, anzi solo il punto x=2 di non derivabilità, per via della simmetria. Facciamo quindi il limite per tale punto della funzione derivata:
\lim\limits_{2 } \frac{x}{\sqrt{x^2 - 4} } = \frac{2}{0} = + \infin
E’ un punto di cuspide, quindi in tale punto la funzione è quasi verticale. Disegniamo una retta piccolina tratteggiata verso l’alto in corrispondenza di x=-2 e x=2.
Settimo punto: concavità.
y''= \frac{ \sqrt{x^2 - 4} -x \frac{2x}{2 \sqrt{x^2 -4} } }{ x^2 - 4 }
Facendo il minimo comune multiplo al numeratore viene:
\frac{ -4}{ (x^2 - 4)\sqrt{x^2 -4} } > 0
Risolviamolo con un falso sistema:
\big\| -4 > 0 \\ \big\| (x^2 - 4)\sqrt{x^2 -4} > 0
Il primo pezzo è per nessuna x, perché è ovviamente sempre falso. Il secondo pezzo è una disequazione con prodotto e lo risolviamo con un altro falso sistema da parte:
\big\| x^2 - 4 > 0 \\ \big\| \sqrt{x^2 -4} > 0
La radice è sempre positiva, tranne nei punti dove essa è zero. Il primo pezzo lo si risolve prendendo le radici di segno opposto e poi prendendo i valori esterni, essendoci un maggiore. In sintesi:
\big\| x<-2 \lor x > 2 \\ \big\| x \ne \pm 2
Prendiamo gli intervalli positivi, ossia proprio:
x<-2 \lor x > 2
Sostituiamo tale risultato nel falso sistema iniziale:
\big\| \nexists x \\ \big\| x<-2 \lor x > 2
Il primo termine lo si scrive nel quadro dei segni con una linea tratteggiata. Quindi abbiamo che la funzione ha concavità verso il basso dappertutto (visto che l’intervallo -2<x<2 non fa parte del dominio). Disegniamo a questo punto la funzione.
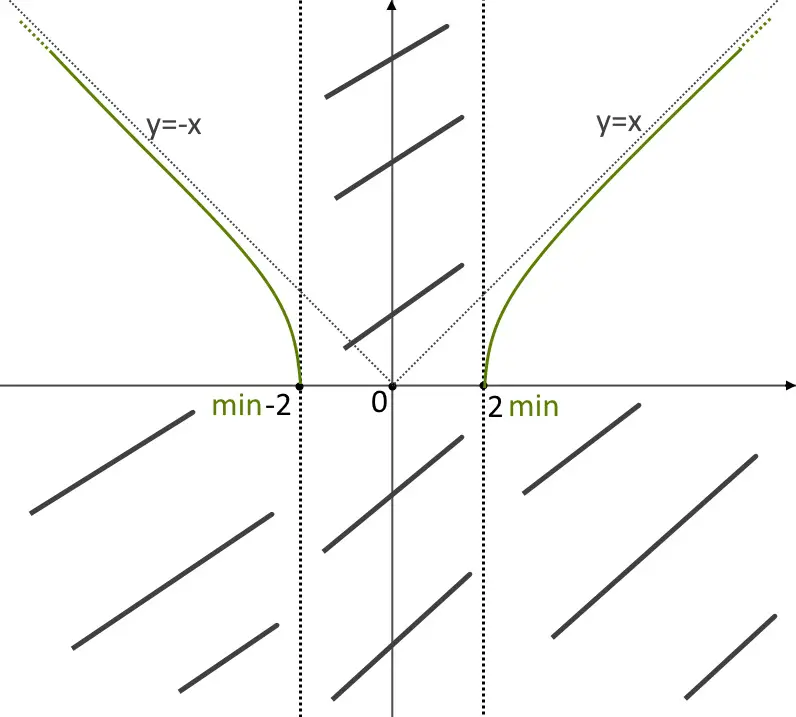
Continuiamo con esercizi svolti sullo studio di una funzione esponenziale!
Studio funzione ESPONENZIALE
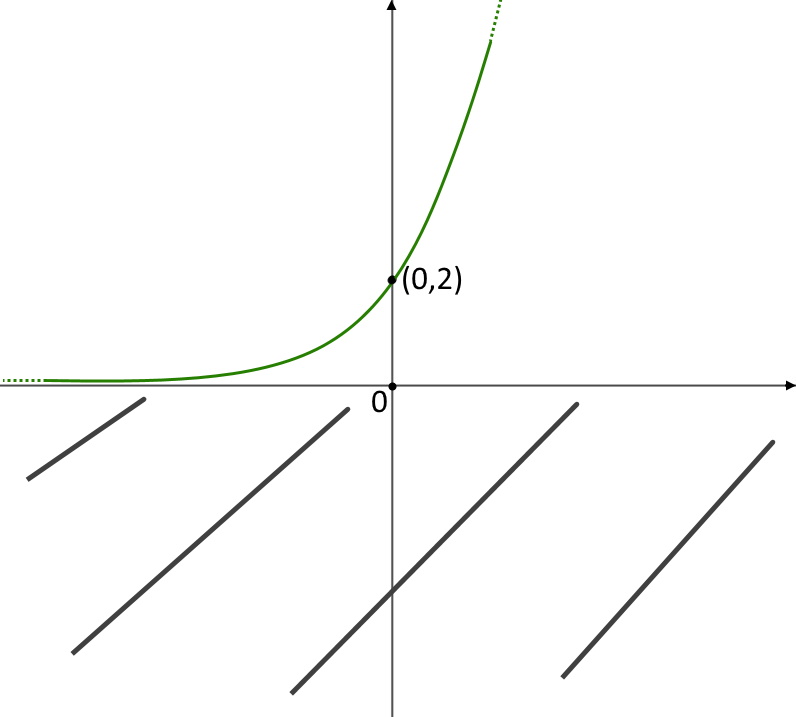
Esercizio 4. y= e^{2x} + e^x
Primo punto: dominio. L’esponenziale è definito in tutto R, non ha problemi!
D: x \in \Reals
Secondo punto: simmetrie. Sostituiamo la -x come sempre:
y= e^{-2x} + e^{-x}
La funzione è chiaramente né dispari né pari. Dobbiamo studiarla in tutto il suo dominio.
Terzo punto: intersezione con assi. Poniamo x=0 per ottenere l’intersezione con l’asse y. (le intersezioni con l’asse x si ottengono direttamente dalla positività):
y= e^0 + e^0 = 1+1=2
La funzione interseca l’asse y nel punto (0,2): segniamocelo.
Quarto punto: studio del segno. Vediamo dove la funzione sta al di sopra.
e^{2x} + e^x \ge 0
(e^x)^2 + e^x \ge 0
Mettiamo in evidenza:
e^x ( e^x +1) \ge 0
Notiamo senza fare nessun calcolo, che l’esponenziale è definito positivo, per cui tutti e due i termini sono positivi. Quindi per ogni x in tutto il dominio la funzione sta al di sopra, cancelliamo la parte di sotto.
Quinto punto: studio estremi. Possiamo studiare sia l’estremo sinistro che l’estremo destro, essendo la funzione definita. Partiamo da quello destro:
\lim\limits_{+ \infin } e^{2x} + e^x = + \infin + \infin =+ \infin
Quindi la funzione tende ad andare verso l’alto, a destra. Vediamo se è un asintoto obliquo:
m= \lim\limits_{+ \infin } \frac{ e^{2x} + e^x }{x} = +\infin
Fa infinito perché l’esponenziale asintoticamente va più veloce ad infinito rispetto alla x.
Poi l’estremo sinistro:
\lim\limits_{- \infin } e^{2x} + e^x = 0+0 = 0
Questo invece è un asintoto orizzontale, ossia la funzione tende ad assumere tale valore, per cui segue la retta y=0. Disegniamo queste due informazioni sul grafico.
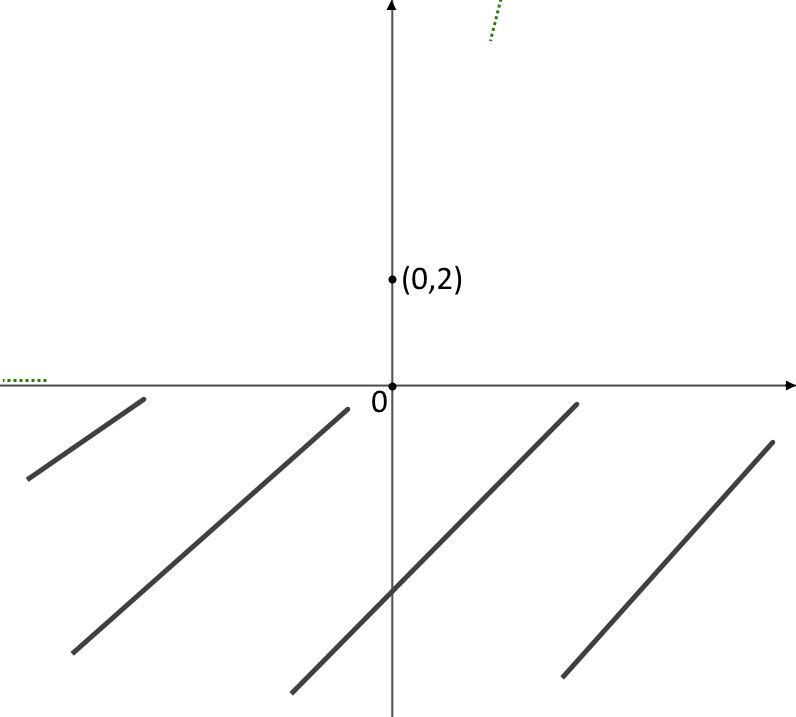
Sesto punto: massimi e minimi. Facciamo la derivata:
y'= 2e^{2x} + e^x
Essa ha lo stesso dominio della funzione di partenza: non ci sono punti di non derivabilità. Andiamo avanti:
2e^{2x} + e^x > 0
Come prima, mettiamo in evidenza:
e^x (2e^x + 1 ) > 0
Entrambi i termini sono certamente positivi perché per definizione e^x > 0 e poi l’altro termine è:
2e^x + 1 > 0 \implies e^x > - \frac{1}{2}
che ovviamente lo è sempre. Quindi il loro prodotto darà sicuramente qualcosa di positivo!
La funzione è quindi sempre crescente! Non ci sono massimi e minimi relativi. Chiaramente, visti gli estremi, capiamo che il massimo assoluto è infinito, ed il minimo assoluto tende a zero ( a meno infinito).
Settimo punto: concavità. Facciamo la derivata seconda:
y''= 4e^{2x} + e^x > 0
e^x ( 4e^x + 1) > 0
Stesso discorso fatto di prima, questo è sempre positivo: quindi ha sempre concavità verso l’alto!
Disegniamo a questo punto la funzione!
Continuiamo col vedere esercizi sullo studio funzioni logaritmiche!
Studio funzioni LOGARITMICHE
Esercizio 5. y= x^2 \cdotp \ln x
Primo punto: dominio. Abbiamo un prodotto fra una funzione polinomiale che non ha problemi di dominio, e poi di un logaritmo, il cui dominio è argomento (quello che sta dentro) maggiore di zero:
D: x>0
Cancelliamo perciò l’altra parte di grafico.
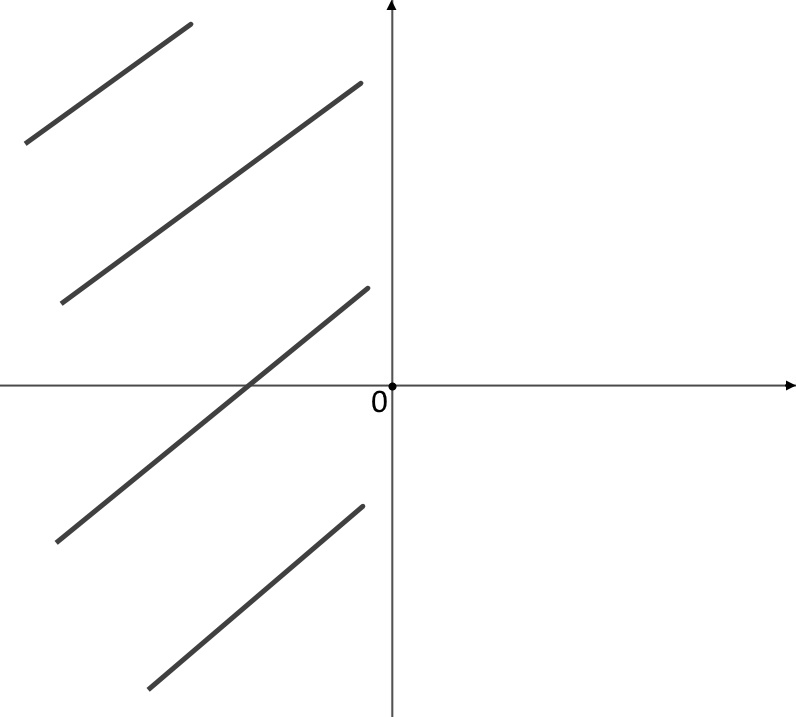
Secondo punto: simmetrie. Qui non possiamo sostituire il -x, perché nel dominio di questo problema una -x non esiste!
Terzo punto: intersezione con assi. Essendo che per x=0 la funzione non esiste, non può chiaramente intersecare l’asse y!
Quarto punto: studio del segno.
x^2 \cdotp \ln x > 0
E’ una disequazione con prodotto, quindi lo risolviamo con un falso sistema:
\big\| x^2 > 0 \\ \big\| \ln x > 0
Al secondo termine abbiamo una disequazione logaritmica, ripetetela se non ve la ricordate!
\big\| x > 0 \\ \big\| x > e^0
\big\| x > 0 \\ \big\| x > 1
Disegniamo il quadro dei segni e prendiamo l’intervallo positivo, sempre ricordando di cancellare tutto quello che non sta su x>0 (il nostro dominio!). Otteniamo che la funzione:
E’ positiva nell’intervallo x>1! Quindi sta al di sopra qui, mentre in 0<x<1 sta al di sotto. La funzione come possiamo vedere interseca quindi l’asse x nel punto x=1, perché ci deve per forza passare!
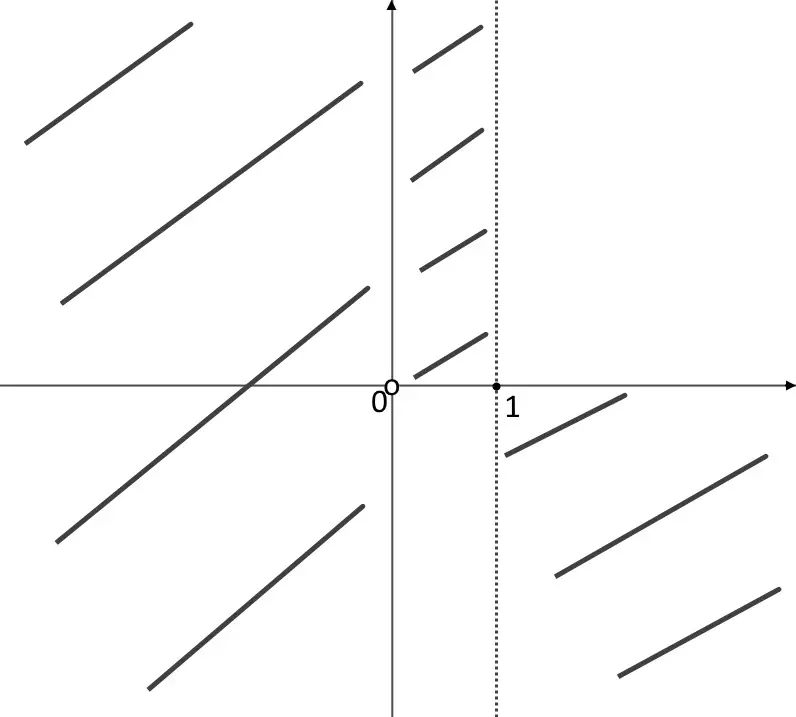
Quinto punto: studio estremi. Studiamo solo l’estremo destro ad infinito. L’estremo sinistro invece non è infinito chiaramente, ma è zero. Partiamo con quello destro:
\lim\limits_{+ \infin } x^2 \cdotp \ln x = + \infin \cdotp (+\infin ) = + \infin
La funzione va semplicemente verso l’alto, vediamo se c’è un asintoto obliquo:
m= \lim\limits_{+ \infin } \frac{ x^2 \cdotp \ln x }{x} = +\infin
Non esiste. Segniamoci però che la funzione va verso l’alto!
L’altro estremo del dominio è 0^+ ! Usando la regola di De L’Hospital:
\lim\limits_{ 0^+ } x^2 \cdotp \ln x =\lim\limits_{ 0^+ } \frac{ \frac{1}{x} }{ \frac{-2x}{x^4} }= 0
Quindi la funzione parte da y=0 in x=0, senza toccarlo tale punto ovviamente.
Sesto punto: massimi e minimi.
y'= 2x \cdotp \ln x + x^2 \frac{1}{x}
Il dominio di questa alla fine è sempre lo stesso, quindi andiamo avanti.
2x \cdotp \ln x + x > 0
Mettiamo in evidenza la x:
x(2 \ln x + 1) > 0
Falso sistema come sempre!
\big\| x > 0 \\ \big\| 2 \ln x + 1 > 0
\big\| x > 0 \\ \big\| \ln x > - \frac{1}{2}
Applichiamo sempre la solita formula per le disequazioni logaritmiche ed otteniamo:
\big\| x > 0 \\ \big\| x > e^{- \frac{1}{2} }
Facciamo il quadro dei segni per vedere massimi e minimi (ricordandoci sempre che la funzione solo in x>0 esiste).
Notiamo quindi che x=e^{- \frac{1}{2} } è il punto di minimo relativo della funzione. Ad esso corrisponde una:
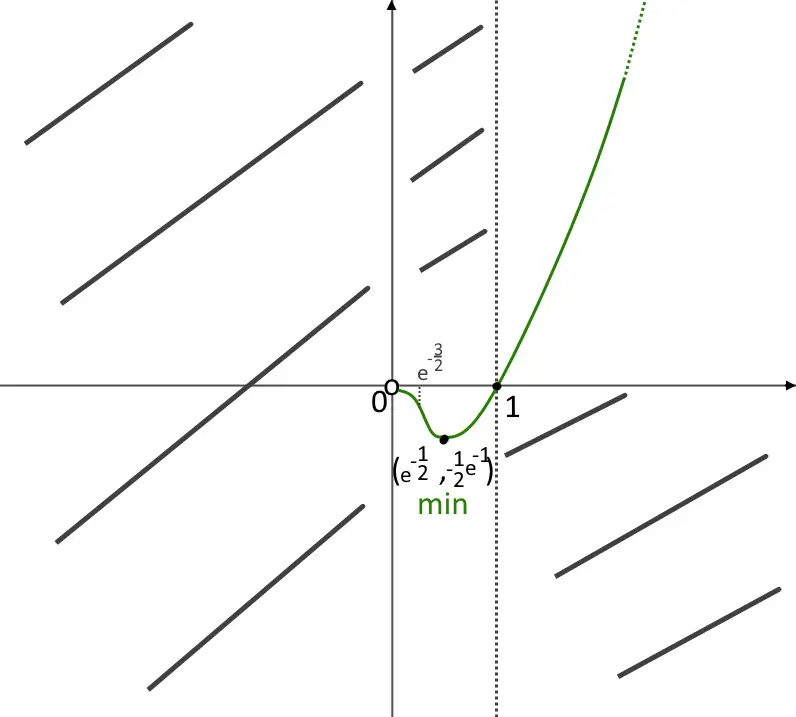
y=(e^{- \frac{1}{2} })^2 \ln e^{- \frac{1}{2} } = -\frac{1}{2} e^{-1}
Che andiamo a segnare nel grafico.
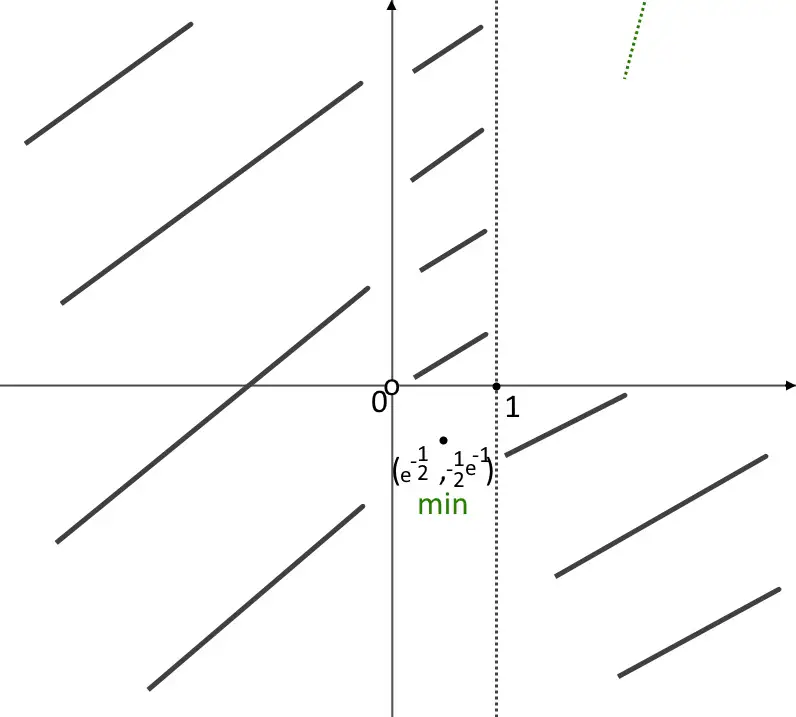
Settimo punto: concavità.
y''= 2 \ln x +1+ x \frac{2}{x}
2 \ln x + 3 > 0
Quindi:
\ln x > - \frac{3}{2}
x > e^{- \frac{3}{2} }
Facendo lo schema dei segni solo per questo, otteniamo che dopo questo punto la concavità è verso l’alto.
A questo punto abbiamo tutto, disegniamo il grafico!
Continuiamo col vedere esercizi svolti sullo studio funzioni goniometriche!
Studio funzioni GONIOMETRICHE
Esercizio 6. y= \tg x +\sin x in [0,2 \pi]
Primo punto: dominio. Qui il dominio già è ristretto per le funzioni goniometriche ad un intervallo, che nel nostro caso qui è [0,2 \pi] . Questo perché la funzione è periodica e quindi si ripete, e noi la studiamo solo in un intervallo. Il seno non ha problemi di dominio, la tangente sì:
D: x \ne \frac{\pi}{2} + k\pi
E nel nostro intervallo abbiamo quindi due punti di discontinuità:
D: x \ne \frac{\pi}{2} \land x \ne \frac{3}{2} \pi
Secondo punto: simmetrie. Nelle funzioni goniometriche queste non si studiano.
Terzo punto: intersezione con assi. Imponiamo x=0:
y= \tg 0 +\sin 0 = 0
Quindi la funzione interseca l’asse y in y=0. Questo rappresenta tra l’altro anche l’estremo sinistro del dominio.
Quarto punto: studio del segno.
\tg x +\sin x \ge 0
\frac{ \sin x }{\cos x } +\sin x \ge 0
Facciamo il minimo comune multiplo:
\frac{ \sin x +\sin x \cos x}{\cos x } \ge 0
\big\| \sin x +\sin x \cos x \ge 0 \\ \big\| \cos x > 0
Questa è una disequazione goniometrica. Partiamo dal secondo termine che ha come soluzione:
0 < x < \frac{\pi}{2} \lor \frac{3}{2}\pi < x < 2 \pi
Per il primo, risolviamolo da parte, mettiamo in evidenza il seno:
\sin x (1 + \cos x ) \ge 0
E lo risolviamo a sua volta con un altro falso sistema:
\big\| \sin x \ge 0 \\ \big\| 1 + \cos x \ge 0
\big\| 0 \le x \le \pi \\ \big\| \forall x
Prendiamo l’intervallo positivo, ossia 0 \le x \le \pi
Sostituiamo i risultati ottenuti nel falso sistema iniziale:
\big\| 0 \le x \le \pi \\ \big\| 0 < x < \frac{\pi}{2} \lor \frac{3}{2}\pi < x < 2 \pi
Gli intervalli positivi, ossia dove la funzione poi sta sopra sono:
0 \le x < \frac{\pi}{2} \land \pi \le x < \frac{3}{2}\pi
Da questa notiamo anche che la funzione tocca l’asse x quindi nei punti:
x=0, x=\pi
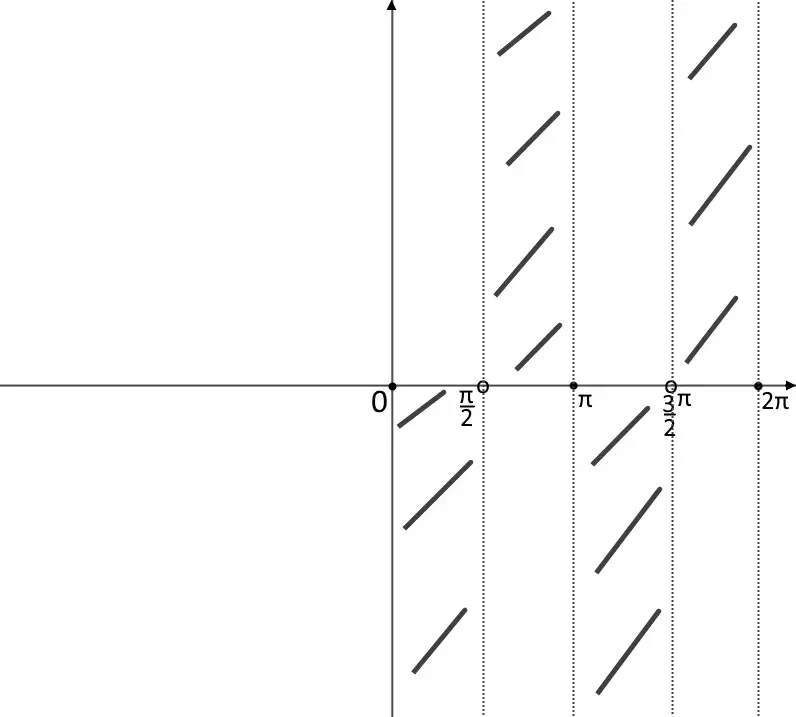
Quinto punto: studio estremi. L’estremo sinistro lo abbiamo già fatto, ora passiamo a quello destro, ossia x=2\pi
Questo è un punto in cui la funzione è continua, quindi non serve fare il limite:
y= \tg 2\pi +\sin 2\pi = 0
Nel punto x=2\pi la funzione assume valore y=0, segniamocelo come sempre sul grafico.
Siamo in un intervallo chiuso, quindi non ci sono gli estremi all’infinito. Passiamo dunque ai punti di discontinuità.
\lim\limits_{ \frac{\pi}{2}^- } \tg x +\sin x = + \infin +1 = + \infin
\lim\limits_{ \frac{\pi}{2}^+} \tg x +\sin x = -\infin +1 = - \infin
Per cui la retta X=\frac{\pi}{2} è un asintoto verticale, disegniamolo con una retta tratteggiata verticale.
\lim\limits_{ \frac{3\pi}{2}^- } \tg x +\sin x = + \infin -1 = + \infin
\lim\limits_{ \frac{3\pi}{2}^+ } \tg x +\sin x = - \infin -1 = - \infin
Anche questo è quindi un altro asintoto verticale. Andiamo a segnare quindi gli estremi della funzione ed il loro comportamento nell’intorno di questi punti.
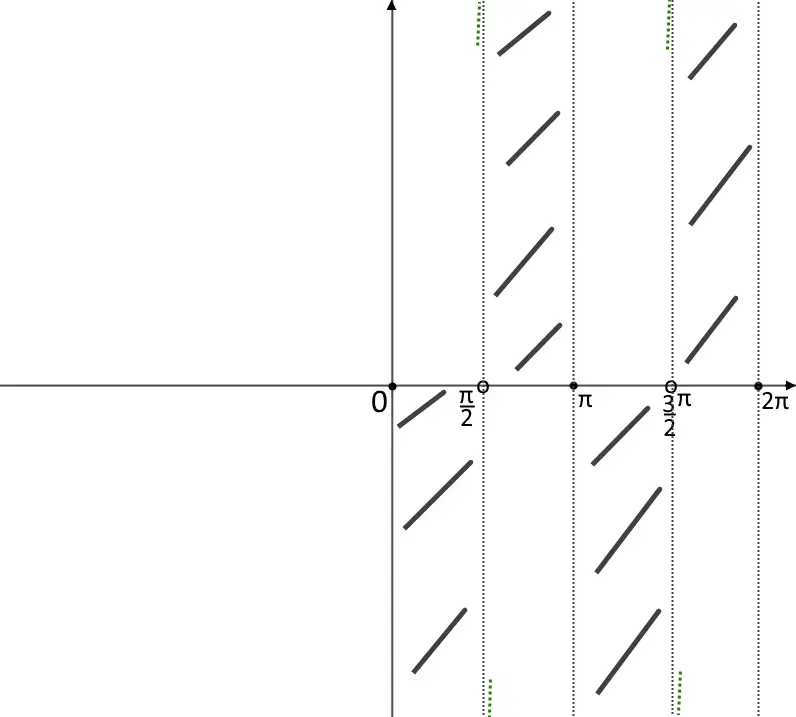
Sesto punto: massimi e minimi. Vedendo nella tabella delle derivate per la tangente segue che:
y' = \frac{1}{\cos^2 x} + \cos x
Il dominio della derivata è lo stesso, quindi non ci sono punti di non derivabilità.
\frac{1 + \cos^3 x}{\cos^2 x} > 0
\big\| \cos^3 x > -1 \\ \big\| \cos^2 x > 0
Il secondo termine è ovviamente sempre positivo quindi lo è sempre tranne nei punti in cui è uguale a zero, ma è uguale a zero proprio nei punti che non fanno parte del dominio. Quindi esso è \forall x . Il primo pezzo è ovviamente sempre > -1, ma tranne nel punto in cui è esattamente -1, ossia in \pi
\big\| x \ne \pi \\ \big\| \forall x
Vediamo nello schema il classico comportamento di un flesso orizzontale. Ossia la funzione cambia concavità. Per il resto come sospettavamo i massimi assoluti e minimi assoluti sono ad infinito chiaramente, come avevamo visto calcolando gli asintoti prima.
Settimo punto: concavità.
In realtà questo è un passaggio che si può anche non fare in questo caso, perché le concavità sono ovvie visti gli altri indizi che abbiamo. Una cosa importante che dovete tenere a mente è: lo studio della concavità si fa solo quando è possibile farlo: a volte le derivate (soprattutto delle frazioni) sono incalcolabili, e quindi non fa niente saltare questo passaggio.
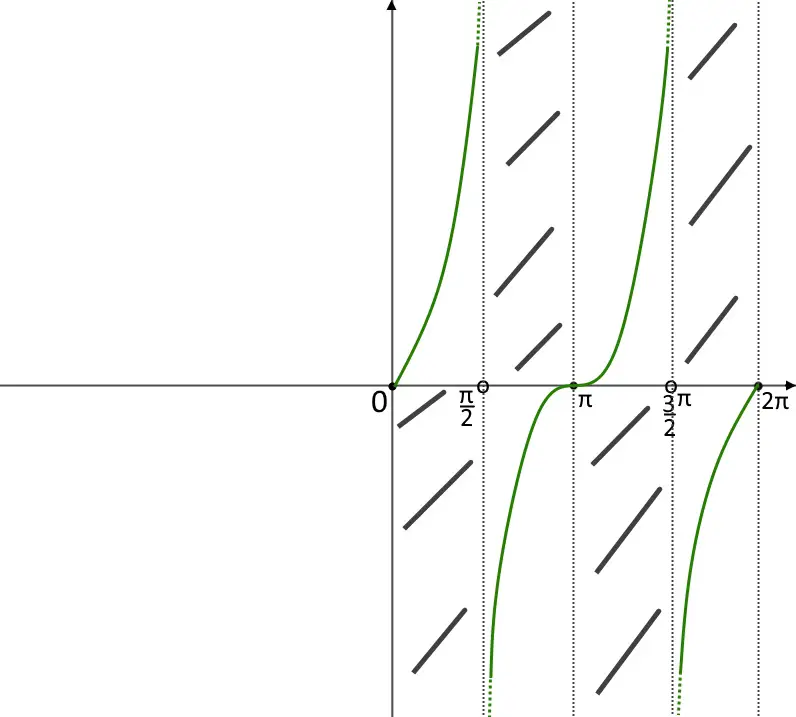
Adesso vediamo un esercizio svolto un po’ diverso: studio di una funzione partendo dal grafico.
Studio funzione partendo dal grafico
Esercizio 7. Studiamo la seguente funzione, partendo dal grafico.
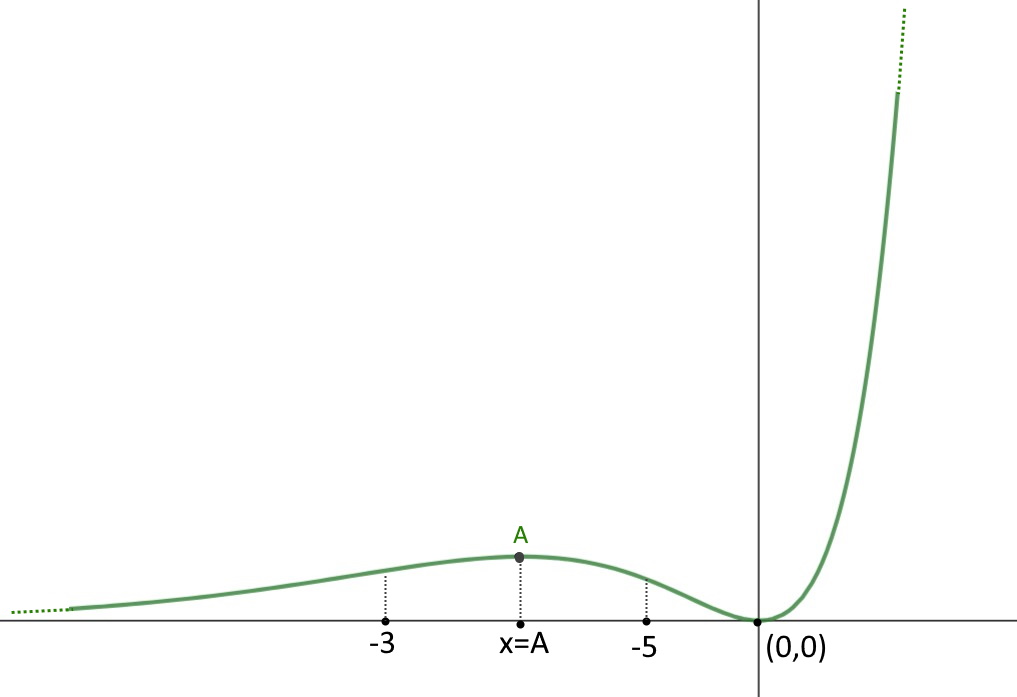
In pratica dobbiamo effettuare il processo inverso di quello visto fino ad ora, seguendo però sempre gli stessi 7 punti!
Primo punto: dominio. Osserviamo il grafico della funzione. Non ci sono buchi (punti di discontinuità) né null’altro: la funzione è definita in tutto R come si vede.
Secondo punto: simmetrie. Osserviamo la parte destra, e poi la parte sinistra: non ci sono simmetrie né di tipo pari né di tipo dispari, la funzione non ha simmetrie.
Terzo punto: intersezione con assi. L’asse delle y viene intersecato nel punto x=0, mentre l’asse x viene intersecato anch’esso nello stesso punto. Non ce ne sono altri.
Quarto punto: studio del segno. La funzione si vede facilmente che è sempre positiva, perché non assume mai valori nella parte inferiore del grafico.
Quinto punto: estremi e asintoti. Esistono entrambi gli estremi ad infinito chiaramente, visto che la funzione è definita in tutto R. Notiamo che a + infinito la funzione tende verso l’alto, quindi a + infinito. A – infinito invece la funzione tende verso l’asse x, ossia tende ad assumere il valore di y=0, questo è sinonimo di asintoto orizzontale!
Sesto punto: massimi e minimi. Il punto di massimo assoluto è sicuramente y=+infinito come si vede. Mentre il punto di minimo assoluto è y=0, cui corrisponde x=0. Poi abbiamo anche il punto A che è di massimo relativo.
Settimo punto: concavità. Qui basta osservare la curva della funzione: da meno infinito fino a x=-5 la concavità si nota essere verso l’alto (quindi derivata seconda positiva), poi in -5<x<-3 cambia concavità e diventa negativa, poi da x>-3 fino a più infinito la concavità è verso l’alto (quindi derivata seconda positiva in tale intervallo).
In questa pagina abbiamo visto un argomento d’esame, molto difficile: esercizi svolti sullo studio di una funzione. Visto che gli argomenti che servono per questo argomento sono tanti, come avete visto, potete continuare a studiare sul nostro sito matematica che altro ancora!
Per approfondire:
https://it.wikipedia.org/wiki/Studio_di_funzione
Per vedere se avete fatto bene il grafico, vi consiglio di controllare scrivendo la funzione su Geogebra:
https://www.geogebra.org/calculator
Studio di una funzione esercizi svolti.
funzioni