Disequazioni irrazionali ESERCIZI
Disequazioni irrazionali ESERCIZI: 15 esercizi SVOLTI! In questa pagina vedremo tutti i tipi di disequazioni irrazionali che potrebbero uscire nella verifica in classe, ed impareremo a capire come si svolgono. Gli esercizi saranno spiegati passo dopo passo, con calma, senza saltare nessun passaggio. Prima, date un occhiata e ripetete un attimo la logica che c’è dietro le equazioni irrazionali, prima di passare alle disequazioni irrazionali. Ma iniziamo subito!
Indice
- Disequazioni del tipo: \sqrt{A(x)} \lessgtr k
- Disequazioni del tipo: \sqrt{A(x)} < B(x)
- Disequazioni del tipo: \sqrt{A(x)} > B(x)
- Disequazioni irrazionali con più radici
Iniziamo subito a vedere le disequazioni irrazionali esercizi!
Disequazioni irrazionali esercizi:
\sqrt{A(x)} \lessgtr k
In questo capitoletto vedremo tutti i casi che possono uscire, quindi con k positivo, negativo…disequazioni con maggiore, minore…iniziamo, prendete appunti!
Ciò che lega tutti questi esercizi del primo tipo sono le CE, che bisogna sempre farle nel caso di una radice con indice pari!

Esercizio 1. \sqrt{ 7-x } > 2
La primissima cosa da fare in queste disequazioni, come in tutte le altre, sono la scrittura delle condizioni di esistenza. Questo perché esse ci permettono alla fine dell’esercizio di capire se la soluzione deve essere scartata o tenuta!
Come potete vedere nelle formule scritte sopra, per una radice con indice pari (quando non c’è scritto nulla vuol dire che l’indice è 2, come in questo caso) le CE significa scrivere il radicando (cioè ciò che c’è dentro la radice) maggiore o uguale di zero.
CE: 7-x \ge 0 \implies -x \ge -7 \implies x \le 7
Solo a questo punto possiamo passare allo svolgimento dell’esercizio. A secondo membro abbiamo un numero positivo (2): quando abbiamo numeri positivi a destra l’esercizio va sempre svolto come segue: eleviamo tutto al quadrato, in modo da levare la radice.
( \sqrt{ 7-x })^2 > 2^2
La radice ce la leviamo dalle scatole:
7-x > 4
E questa è una disequazione lineare che sappiamo risolvere!
-x > 4-7
-x > -3
Cambiamo tutto di segno (ricordatevi che quando si cambia tutto di segno si cambia anche il segno della disequazione, quindi qui diventa minore).
x < 3
Ora dobbiamo controllare se tale soluzione va bene. Per fare ciò si mette la soluzione a sistema con le CE.
\begin{cases} x<3 \\ x \le 7 \end{cases}
In un sistema significa prendere gli intervalli comuni, quindi vediamo il seguente schema.
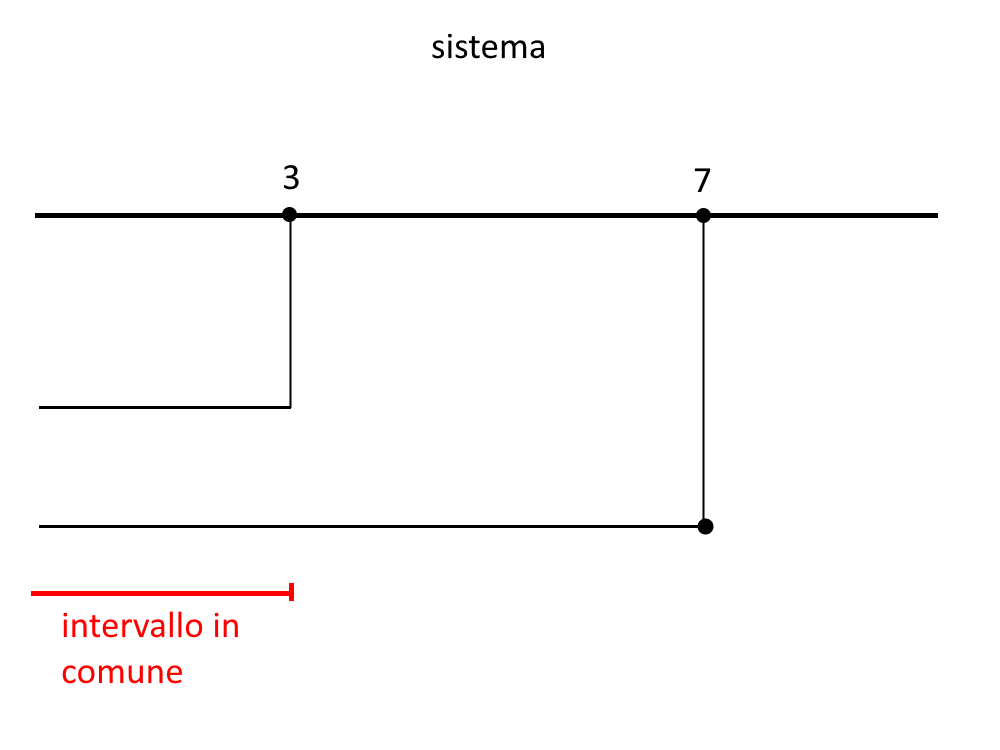
La soluzione finale è sempre: x<3
Esercizio 2. \sqrt{ 6x - 4 } > -1
Come primo punto scriviamo sempre le condizioni di esistenza!
CE: 6x-4 \ge 0 \implies 6x \ge 4 \implies x \ge \frac{2}{3}
Fatto ciò, adesso pensiamo all’esercizio: abbiamo una radice a sinistra che per definizione è maggiore o uguale a zero, e poi a destra abbiamo un numero negativo. La radice è SEMPRE maggiore di -1, perchè la radice è un qualcosa che per definizione o è positiva (cioè vale 2, 3,4 ecc.) o al massimo è uguale a 0. Quindi più grande di -1 lo è SEMPRE!
Non c’è bisogno qui di elevare al quadrato perché la soluzione è direttamente:
\forall x
Ossia, per qualsiasi x la radice è più grande di -1!
Adesso il passaggio finale è sempre uguale però: mettiamo a sistema soluzione e CE!
\begin{cases} \forall x \\ x \ge \frac{2}{3} \end{cases}
Il \forall x in uno schema si scrive con una linea continua.
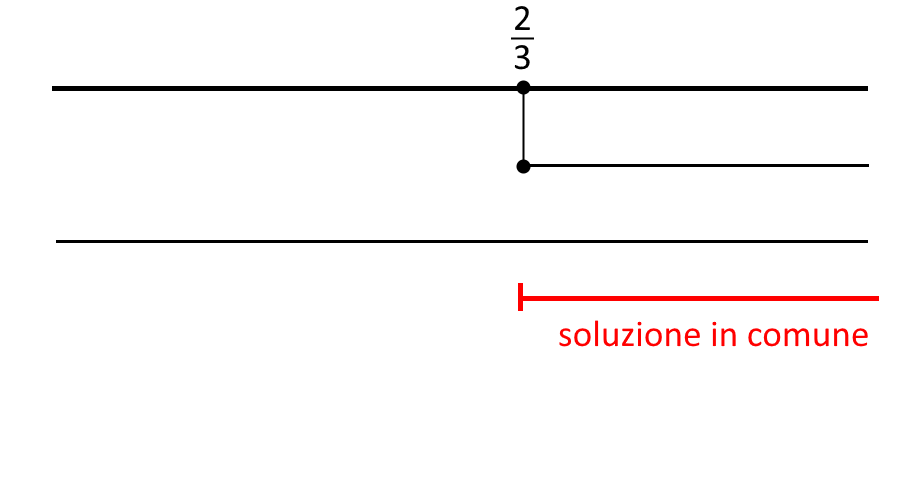
Prendiamo gli intervalli comuni, ossia proprio:
x \ge \frac{2}{3}
Esercizio 3. \sqrt{ 9-5x } < 4
Condizioni di esistenza della radice con indice pari.
CE: 9-5x \ge 0 \implies -5x \ge -9 \implies x \le \frac{9}{5}
Qui abbiamo a destra un numero positivo ( che ci deve subito far venire in mente di elevare tutto al quadrato ) e a sinistra una sola radice. Abbiamo un minore ma ciò non rende diverso l’esercizio dal primo, dove avevamo un maggiore.
Quindi eleviamo semplicemente tutto al quadrato:
(\sqrt{ 9-5x })^2 < 4^2
9-5x < 16
Risolviamo questa disequazione!
-5x < 7
Cambiamo di segno, e dividiamo per 5:
x > - \frac{7}{5}
Adesso mettiamo a sistema come sempre soluzione e CE:
\begin{cases} x > - \frac{7}{5} \\ x \le \frac{9}{5} \end{cases}
L’intervallo comune è:
- \frac{7}{5} < x \le \frac{9}{5}
Esercizio 4. \sqrt{ x -1 } < -7
CE: x-1 \ge 0 \implies x \ge 1
In questo esercizio vediamo l’ultimo caso: radice a sinistra con un numero negativo a destra, con un minore.
Come detto prima la radice per definizione è positiva o uguale a zero al massimo. Quindi essa non potrà mai essere minore di -7, ossia non può MAI essere più piccola di -7, ossia non sarà mai uguale ad esempio a -8,-9 ecc.
Quindi non esiste soluzione, perchè la radice è \ge 0 (ed è anche per questo che facciamo le CE ponendo il radicando \ge 0 ).
La soluzione è: \nexists x
E’ inutile in questo caso mettere a sistema perché ci ridarebbe sempre questo risultato. Però se non siete convinti potete anche mettere a sistema anche in questo caso CE e soluzione. Il \nexists x in uno schema si disegna con una linea tratteggiata.
Continuiamo con altre disequazioni irrazionali esercizi svolti!
Esercizio 5. \sqrt[3]{ x-2 } > -2
Ora vediamo il caso più semplice in assoluto, cioè quello con radice con indice dispari.
E’ il caso più semplice perché NON bisogna scrivere le condizioni di esistenza. Inoltre non bisogna badare al fatto che il numero sia positivo o negativo, è sempre lo stesso procedimento!
L’unico passaggio da fare è elevare alla terza in questo caso…STOP
(\sqrt[3]{ x-2 })^3 > (-2)^3
x-2 > -8
Se non avete capito perché fa -8 ve lo spiego meglio ora:
(-2)^3 = -2 \cdotp -2 \cdotp -2 = 4 \cdotp -2 = -8
Torniamo alla disequazione:
x > -8+2
x > -6
Ed ecco fatto! Non c’è neanche il sistema finale perché non ci sono le CE!
Esercizio 6. \sqrt{ 1 + 8x^2 } \ge 3
Per chiarire eventuali dubbi adesso vediamo una disequazione irrazionale con un maggiore o uguale. Vi anticipo già che non cambia assolutamente nulla.
CE: 1 + 8x^2 \ge 0 \implies 8x^2 \ge -1
\implies x^2 \ge - \frac{1}{8}
Abbiamo una x al quadrato che è sempre positiva o uguale a zero. Quindi essa è SEMPRE maggiore di un numero negativo!
CE: \forall x
In pratica le CE ci stanno dicendo che qualsiasi soluzione verrà fuori andrà bene!
Abbiamo una radice, e poi un numero positivo a destra: quindi eleviamo al quadrato entrambi i membri.
( \sqrt{ 1 + 8x^2 } )^2 \ge 3^2
1 + 8x^2 \ge 9
Isoliamo la x:
8x^2 \ge 8
x^2 \ge 1
Questa si risolve prendendo le due radici di segno opposto, e poi prendendone i valori esterni essendoci un maggiore. Quindi:
x \le -1 \lor x \ge 1
Per le CE questa soluzione va bene!
Continuiamo con altre disequazioni irrazionali esercizi svolti!
Disequazioni irrazionali:
\sqrt{A(x)} < B(x)
Useremo una formula solo per questi tipi di esercizi. Scriviamo sia il caso del < sia il caso del \le che è la stessa formula ma con l’aggiunta dell’uguale.


Esercizio 7. \sqrt{ x^2 -6x } < 4-x
Tale disequazione è della forma seguente: radice da sola a sinistra, e altro contenente la x a destra. Qui non c’è bisogno di scrivere le CE da parte, perché le mettiamo direttamente dentro al sistema. Se vedete bene le CE sono il primo rigo del sistema della formula! Quindi facciamo tutti i passaggi in uno in pratica.
Applichiamo la formula sopra scritta:
\implies \begin{cases} x^2 -6x \ge 0 \\ 4-x>0 \\ x^2 -6x <( 4-x)^2 \end{cases}
In questi tipi di esercizi non c’è bisogno di pensare al fatto che i numeri possano essere negativi o positivi, semplicemente si applica sempre la formula e si risolve il sistema che esce fuori!
Al primo termine mettiamo una x in evidenza, poi scriviamo il quadrato della parentesi al terzo rigo. Se non vi ricordate la formula del quadrato del binomio essa è:
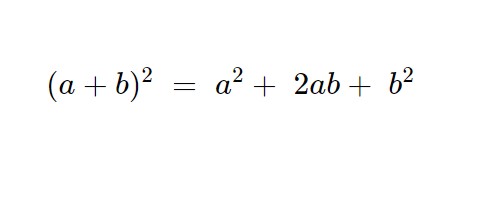
\begin{cases} x(x -6) \ge 0 \\ -x>-4 \\ x^2 -6x < 16+x^2 - 8x \end{cases}
\begin{cases} x(x -6) \ge 0 \\ x<4 \\ 2x < 16 \end{cases}
Il primo rigo lo risolviamo dopo, adesso concludiamo il terzo un attimo. Uno per volta!
\begin{cases} x(x -6) \ge 0 \\ x<4 \\ x < 8 \end{cases}
Il primo termine del sistema è un prodotto in una disequazione, e si risolve da parte con un falso sistema.
\big\| x\ge 0 \\ \big\| x-6 \ge 0
\big\| x\ge 0 \\ \big\| x \ge 6
Come soluzione prendiamo gli intervalli positivi (visto che nella disequazione iniziale del prodotto c’è un maggiore) nel quadro dei segni.
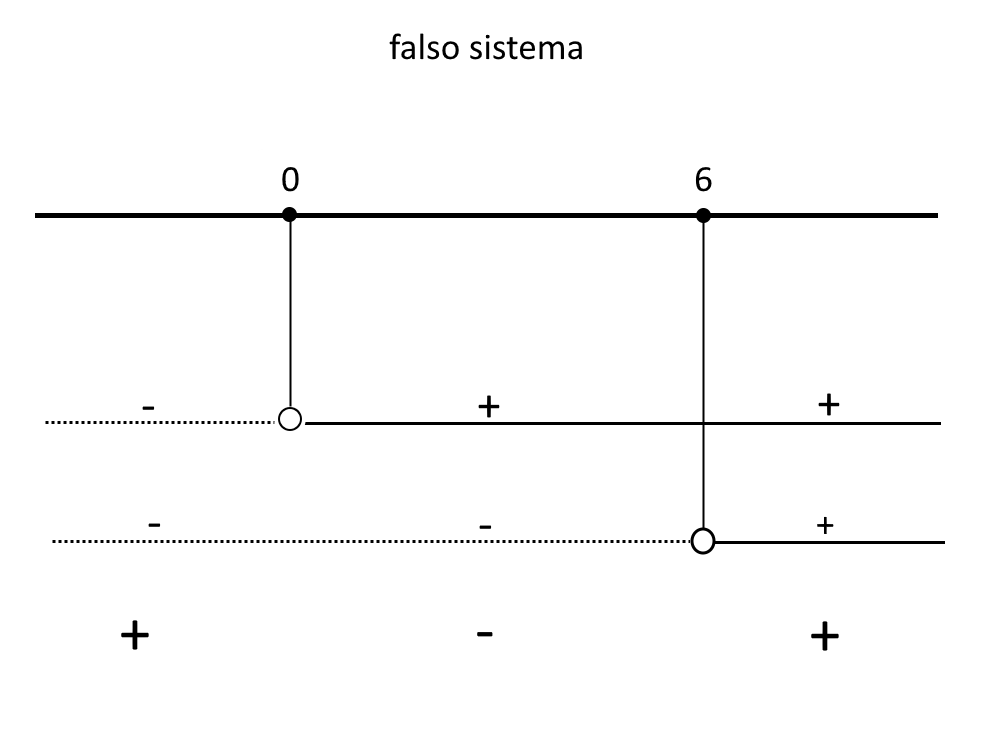
Ossia:
x \le 0 \lor x \ge 6
Sostituiamo nel sistema iniziale questo risultato:
\begin{cases} x \le 0 \lor x \ge 6 \\ x<4 \\ x < 8 \end{cases}
Ed essendo un sistema, mettiamo tutte queste informazioni in uno schema e prendiamo gli intervalli comuni. (ricordatevi che ogni rigo del sistema va su un rigo diverso dello schema).
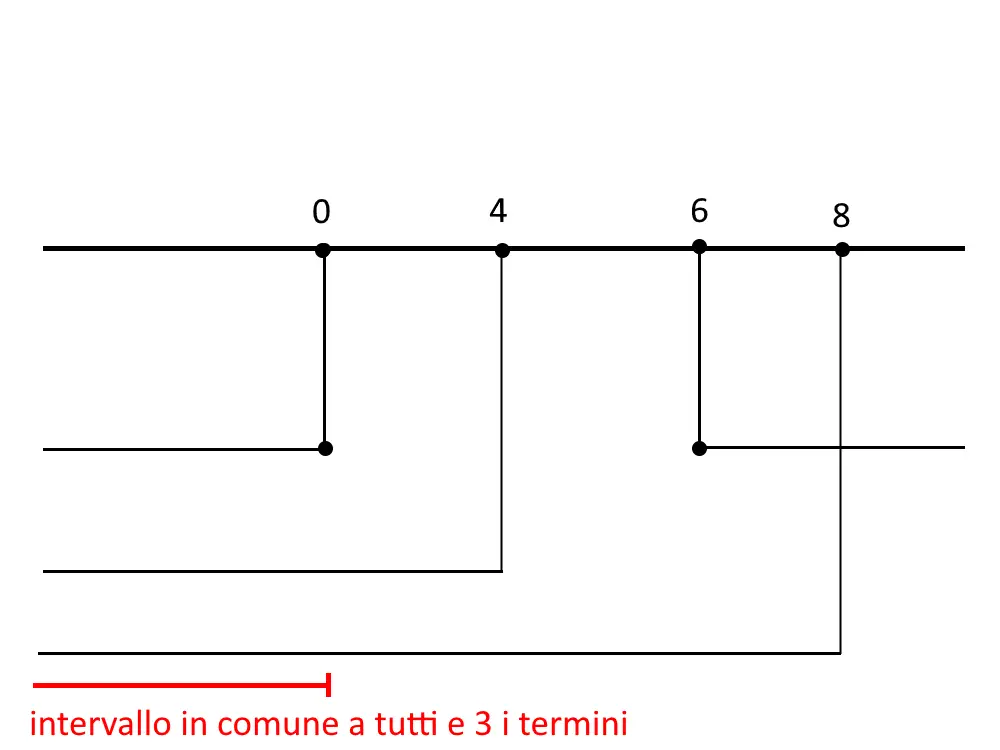
Quindi la soluzione dell’esercizio è:
x \le 0
L’intervallo deve essere comune a tutti e 3 i termini del sistema contemporaneamente!
Esercizio 8. \sqrt{ 14x +2 } -1 < 3x
Come detto nell’esercizio precedente in questo caso non abbiamo bisogno di scrivere le CE da parte all’inizio, perché sono già contenute nel sistema che scriveremo.
Tale disequazione però non ha la forma giusta che vogliamo: noi vogliamo (come nella formula) a sinistra solo la radice e a destra tutto il resto (che contiene una x almeno).
Quindi scriviamo prima:
\sqrt{ 14x +2 } < 3x +1
Ed ora siamo nelle condizioni giuste per applicare la formula e risolvere il seguente sistema.
\begin{cases} 14x +2 \ge 0 \\ 3x +1 > 0 \\ 14x +2 < (3x +1)^2 \end{cases}
\begin{cases} 14x \ge -2 \\ 3x > -1 \\ 14x +2 < 9x^2 +1 +6x \end{cases}
Le prime due disequazioni le sappiamo risolvere! La terza sommiamo un attimo i rispettivi termini simili e portiamo tutto a primo membro:
\begin{cases} x \ge - \frac{1}{7} \\ x > -\frac{1}{3} \\ -9x^2 +8x +1 < 0 \end{cases}
Prendiamo da parte la terza disequazione del sistema, che è una disequazione di secondo grado ( cliccateci sopra per le formule un attimo ). Dobbiamo innanzitutto cambiare di segno perché vogliamo il termine quadratico positivo:
9x^2 -8x -1 > 0
Calcoliamo il discriminante ( o delta-quarti, sono sinonimi):
\frac{\Delta}{4} = ( \frac{b}{2} )^2 - ac = 16+9=25
Discriminante>0 quindi esistono soluzioni, calcoliamole con la seguente formula e poi prendiamone i valori esterni (visto che la disequazione è con un maggiore).
x_{1,2} = \frac{- \frac{b}{2} \pm \sqrt{\frac{\Delta}{4} } }{a} = \frac{4 \pm 5 }{9}
E quindi:
x_1 = \frac{4 + 5 }{9} = 1
x_2 = \frac{4 - 5 }{9} = - \frac{1}{9}
Come detto prima prendiamo i valori interni:
x<- \frac{1}{9} \lor x > 1
Adesso, possiamo sostituire nel sistema e finalmente risolverlo:
\begin{cases} x \ge - \frac{1}{7} \\ x > -\frac{1}{3} \\ x<- \frac{1}{9} \lor x > 1 \end{cases}
Prendiamo gli intervalli comuni a tutti e 3 i termini e quindi la soluzione finale è:
- \frac{1}{7} \le x < -\frac{1}{9} \lor x > 1
Continuiamo con altre disequazioni irrazionali esercizi svolti!
Esercizio 9. \sqrt{ x^2 -5x } -2 \le -x
Iniziamo ad isolare la radice ed a raggiungere la forma della disequazione della formula.
\sqrt{ x^2 -5x } \le 2-x
A questo punto applichiamo la formula e risolviamo il sistema seguente.
\begin{cases} x^2 -5x \ge 0 \\ 2-x > 0 \\ x^2 -5x \le (2-x)^2 \end{cases}
Al primo rigo del sistema mettiamo la x in evidenza, al terzo risolviamo il quadrato del binomio.
\begin{cases} x(x -5) \ge 0 \\ -x > -2 \\ x^2 -5x \le 4+x^2 -4x \end{cases}
Iniziamo a risolvere ciò che sappiamo risolvere e ciò che sembra più facile: il secondo termine del sistema cambiamo di segno ed al terzo sommiamo i rispettivi termini.
\begin{cases} x(x -5) \ge 0 \\ x < 2 \\ -x \le 4 \end{cases}
Non ci rimane che cambiare di segno anche al terzo termine del sistema:
\begin{cases} x(x -5) \ge 0 \\ x < 2 \\ x \ge -4 \end{cases}
A questo punto abbiamo tenuto da parte il primo termine perché è quello più lunghetto, visto che si risolve con un falso sistema:
\big\| x \ge 0 \\ \big\| x-5 \ge 0
\big\| x \ge 0 \\ \big\| x \ge 5
Nel quadro dei segni prendiamo gli intervalli col segno +, visto che la disequazione è con un maggiore.
x \le 0 \lor x \ge 5
A questo punto sostituiamo questo nel sistema iniziale:
\begin{cases} x \le 0 \lor x \ge 5 \\ x < 2 \\ x \ge -4 \end{cases}
Il sistema è completo e risolto: prendiamo ora in uno schema gli intervalli comuni a tutti e 3 i righi. La soluzione finale dell’esercizio è:
-4 \le x \le 0
Esercizio 10. \sqrt{ 4x^2 +13x +15 } \le x-3
La disequazione è già nella forma giusta della formula: cioè radice a sinistra, minore o uguale, e poi a destra il resto. Scriviamo il sistema:
\begin{cases} 4x^2 +13x +15 \ge 0 \\ x-3 > 0 \\ 4x^2 +13x +15 \le (x-3)^2 \end{cases}
Questa volta andiamo in ordine, partiamo dal risolvere il primo termine del sistema.
4x^2 +13x +15 \ge 0
Essa è una disequazione di secondo grado, e quindi calcoliamone il delta:
\Delta = b^2 -4ac = 169 - 240 < 0
Delta<0 in una disequazione con un maggiore vuol dire che c’è sempre soluzione per qualsiasi x:
\forall x
Sostituiamo questo risultato e risolviamo velocemente anche il secondo rigo del sistema:
\begin{cases} \forall x \\ x > 3 \\ 4x^2 +13x +15 \le (x-3)^2 \end{cases}
Prendiamo da parte il terzo termine e svolgiamolo. Tutto come vedete sempre uno per volta, così non avrete mai problemi.
4x^2 +13x +15 \le (x-3)^2
4x^2 +13x +15 \le x^2 + 9 -6x
Anche questa è una disequazione di secondo grado, quindi portiamo tutto a primo membro:
3x^2 +19x +6 \le 0
Calcoliamo il delta:
\Delta = b^2 -4ac = 361 - 72 = 289
Delta>0 in una disequazione con minore vuol dire che esiste soluzione. Calcoliamo le singole soluzioni e poi prenderemo i valori interni.
x_{1,2} = \frac{- b \pm \sqrt{\Delta } }{2a} = \frac{-19 \pm 17 }{6}
Cioè:
x_1 = \frac{-19 + 17 }{6} = \frac{1}{3}
x_2 = \frac{-19 - 17 }{6} = - \frac{1}{6}
E visto che la disequazione è con un minore, si prendono i valori interni:
- \frac{1}{6} \le x \le \frac{1}{3}
Sostituiamo nel sistema che ormai è completo:
\begin{cases} \forall x \\ x > 3 \\ - \frac{1}{6} \le x \le \frac{1}{3} \end{cases}
Notiamo che intervalli comuni a tutti e 3 i termini non ce ne sono, quindi l’esercizio non ha soluzione o è impossibile.
Continuiamo con altre disequazioni irrazionali esercizi svolti!
Disequazioni irrazionali
\sqrt{A(x)} > B(x)
In questo capitoletto, in cui la disequazione sarà la stessa ma caratterizzata da un segno di maggiore, useremo questa formula.


Esercizio 11. \sqrt{ 14x +11 } > x+4
Anche in questo caso non c’è bisogno di scrivere da parte all’inizio le condizioni di esistenza perché sono già contenute nel sistema, come vedete.
La disequazione è già nelle condizioni giuste per applicare la formula: radice a sinistra, maggiore, e il resto con la x a destra.
Per trovare la soluzione dell’esercizio basta risolvere quindi i sistemi seguenti:
\begin{cases} 14x+11 \ge 0 \\ x+4<0 \end{cases} \lor \begin{cases} x+4 \ge 0 \\ 14x +11 > (x+4)^2 \end{cases}
Iniziamo a risolverle, isolando la x a primo membro. All’ultima disequazione svolgiamo il quadrato.
\begin{cases} 14x \ge -11 \\ x<-4 \end{cases} \lor \begin{cases} x \ge -4 \\ 14x +11 > x^2 + 16 + 8x \end{cases}
Si tratta solo di risolvere ogni singola disequazione. Nell’ultima disequazione ora portiamo tutto a primo membro, e sommiamo i rispettivi termini:
\begin{cases} x \ge -\frac{11}{14} \\ x<-4 \end{cases} \lor \begin{cases} x \ge -4 \\ -x^2 +6x -5 > 0 \end{cases}
L’ultima disequazione di secondo grado, che è più lunghetta, la calcoliamo da parte. Iniziamo a cambiargli di segno visto che per comodità vogliamo sempre il termine quadratico positivo:
x^2 -6x +5 < 0
Calcoliamo il delta-quarti, visto che il secondo coefficiente è pari.
\frac{\Delta}{4} = ( \frac{b}{2} )^2 - ac = 9-5=4
Discriminante>0 ed allora calcoliamone le soluzioni con la formula seguente.
x_{1,2} = \frac{- \frac{b}{2} \pm \sqrt{\frac{\Delta}{4} } }{a} = \frac{3 \pm 2 }{1}
Visto che stiamo parlando di disequazione, e visto che c’è un minore prendiamo i valori interni di questi:
x_1 = 3+2=5
x_2 = 3-2=1
Ossia:
1 < x < 5
Abbiamo ora il sistema completo, sostituiamo.
\begin{cases} x \ge -\frac{11}{14} \\ x<-4 \end{cases} \lor \begin{cases} x \ge -4 \\ 1 < x < 5 \end{cases}
Abbiamo due sistemi: risolviamone uno per volta. Partiamo dallo schema del primo.
Nel sistema si prendono gli intervalli comuni. Nel primo sistema che non c’è nulla in comune scriviamo:
\nexists x
Adesso passiamo al secondo sistema. Prendiamo in comune:
1 < x < 5
Visto che il simbolo fra i due sistemi \lor significa unione si devono unire le due soluzioni.
\nexists x \lor 1 < x < 5
che è equivalente a:
1 < x < 5
Esercizio 12. x-3 - \sqrt{ 2x^2 -18 } < 0
La forma non è quella giusta per la formula, isoliamo quindi la radice a primo membro.
- \sqrt{ 2x^2 -18 } < -x+3
Anche qui non va bene, perché vogliamo la radice e basta, quindi cambiamo tutto di segno e leviamoci quel segno – dalle scatole.
\sqrt{ 2x^2 -18 } < x-3
Ora sì che possiamo quindi risolvere i due sistemi:
\begin{cases} 2x^2 -18 \ge 0 \\ x-3<0 \end{cases} \lor \begin{cases} x-3 \ge 0 \\ 2x^2 -18 < (x-3)^2 \end{cases}
Scriviamo un attimo bene le due disequazioni più semplici:
\begin{cases} 2x^2 -18 \ge 0 \\ x<3 \end{cases} \lor \begin{cases} x \ge 3 \\ 2x^2 -18 < (x-3)^2 \end{cases}
Risolviamo la prima disequazione di secondo grado, ossia:
2x^2 -18 \ge 0
2x^2 \ge 18
Dividiamo per 2:
x^2 \ge 9
Queste si risolvono prendendo i valori esterni (visto il maggiore) delle due radici con segno opposto:
x \le -3 \lor x \ge 3
Passiamo ora all’altra disequazione di secondo grado del sistema che rimane:
2x^2 -18 < (x-3)^2
2x^2 -18 < x^2 + 9 -6x
Portiamo tutto a primo membro:
2x^2 -18 -x^2 - 9 +6x < 0
x^2 +6x -27 < 0
Calcoliamo il discriminante:
\frac{\Delta}{4} = (\frac{b}{2})^2 -ac = 9 + 27 = 36
Delta>0 in una disequazione con minore vuol dire che esiste soluzione. Troviamole con:
x_{1,2} = \frac{- \frac{b}{2} \pm \sqrt{\frac{\Delta}{4} } }{a} = \frac{-3 \pm 6 }{1}
Ossia le singole soluzioni sono:
x_1 = -3+6=3
x_2 = -3-6=-9
E visto il minore della disequazione prendiamo i valori interni:
-9<x<3
Sostituiamo le informazioni ottenute nel sistema che ora è completo di tutti i termini.
\begin{cases} x \le -3 \lor x \ge 3 \\ x<3 \end{cases} \lor \begin{cases} x \ge 3 \\ -9<x<3 \end{cases}
Capiamoli uno per volta. Iniziamo dal primo, che essendo un sistema, dobbiamo prendere i valori comuni, ossia:
x<3
Poi dal secondo sistema ricaviamo:
\nexists x
Uniamole e riotteniamo x<3 !
Continuiamo con altre disequazioni irrazionali esercizi svolti!
Esercizio 13. \sqrt{ x^2 +7 } - x +7 \ge 0
Isoliamo la radice a primo membro:
\sqrt{ x^2 +7 } \ge x-7
Svolgiamo l’esercizio con i soliti due sistemi, questa volta col maggiore o uguale:
\begin{cases} x^2 +7 \ge 0 \\ x-7<0 \end{cases} \lor \begin{cases} x-7 \ge 0 \\ x^2 +7 \ge (x-7)^2 \end{cases}
Isoliamo la x nelle prime tre disequazioni. L’ultima ce la teniamo da parte.
\begin{cases} x^2 \ge -7 \\ x<7 \end{cases} \lor \begin{cases} x \ge 7 \\ x^2 +7 \ge (x-7)^2 \end{cases}
Pensiamo ora al primo termine del sistema. Si ha un quadrato che è per definizione positivo o al massimo uguale a zero, e quindi è SEMPRE più grande di -7, cioè è ovviamente più grande di un numero negativo! La soluzione di questa è:
\forall x
Pensiamo all’ultima disequazione ora:
x^2 +7 \ge (x-7)^2
Svogliamo il quadrato:
x^2 +7 \ge x^2 + 49 - 14x
Semplifichiamo la x^2 e portiamo le x a primo membro:
14x \ge 42
Dividiamo per 14:
x \ge 3
Sostituiamo il tutto nei due sistemi che ora sono completi:
\begin{cases} \forall x \\ x<7 \end{cases} \lor \begin{cases} x \ge 7 \\ x \ge 3 \end{cases}
Il primo sistema ha come intervalli comuni:
x<7
Il secondo sistema ha come soluzioni comuni:
x \ge 7
Uniamo le due soluzioni adesso:
x<7 \lor x \ge 7
Ossia tutte le soluzioni in pratica.
\forall x \in \Reals
Esercizio 14. \sqrt{ (x+2)^2 -4x -8 } -x \ge 2
Isoliamo la radice innanzitutto.
\sqrt{ (x+2)^2 -4x -8 } \ge x+2
Applichiamo la formula e scriviamo i due sistemi:
\begin{cases} (x+2)^2 -4x -8 \ge 0 \\ x+2<0 \end{cases} \lor \begin{cases} x+2 \ge 0 \\ (x+2)^2 -4x -8 \ge (x+2)^2 \end{cases}
Una cosa alla volta. Partiamo dal primo termine:
(x+2)^2 -4x -8 \ge 0
Svolgiamo il quadrato:
x^2 + 4 +4x -4x -8 \ge 0
x^2 -4 \ge 0
Isoliamo la x:
x^2 \ge 4
Questo l’abbiamo visto tante volte insieme: si risolve prendendo le due radici con segno diverso e poi i valori esterni (per via del maggiore):
x \le -2 \lor x \ge 2
Sostituiamo questo termine nel sistema:
\begin{cases} x \le -2 \lor x \ge 2 \\ x<-2 \end{cases} \lor \begin{cases} x \ge -2 \\ (x+2)^2 -4x -8 \ge (x+2)^2 \end{cases}
Scriviamo da parte l’ultima disequazione:
(x+2)^2 -4x -8 \ge (x+2)^2
Senza risolvere i quadrati, visto che sono uguali a primo membro e a secondo, li semplifichiamo direttamente.
-4x -8 \ge 0
-4x \ge 8
Che ha come soluzione:
x \le -2
Sostituiamo nei sistemi che ora sono finiti:
\begin{cases} x \le -2 \lor x \ge 2 \\ x<-2 \end{cases} \lor \begin{cases} x \ge -2 \\ x \le -2 \end{cases}
Vediamo che il primo sistema ha soluzioni comune x<-2
Il secondo sistema ha come soluzione comune solo la singola x=2.
Uniamole ed otteniamo:
x \le -2
Continuiamo con altre disequazioni irrazionali esercizi svolti!
Disequazioni irrazionali esercizi con più radici
Esercizio 15. \sqrt[3]{ 3-5x } + \sqrt[3]{ (3-5x)^2 } \le 0
Qui abbiamo più radici con indice dispari (che come detto in precedenza non hanno problemi di CE, cioè non dobbiamo mai scriverle). Quello che facciamo è portare una radice a sinistra ed una a destra:
\sqrt[3]{ 3-5x } \le - \sqrt[3]{ (3-5x)^2 }
Per le radici con indice dispari nemmeno il segno – è un problema. Abbiamo fatto così perché ora possiamo elevare tutto alla terza ed eliminare entrambe le radici!
( \sqrt[3]{ 3-5x })^3 \le (- \sqrt[3]{ (3-5x)^2 } )^3
3-5x \le - (3-5x)^2
Il segno – rimane perché abbiamo elevato alla terza, cioè un numero dispari di volte. Ora svolgiamo il quadrato a secondo membro, stando attenti a non levare il segno – che sta davanti alla parentesi!
3-5x \le -(9+25x^2 - 30x)
Moltiplichiamo il – per tutti i termini nella parentesi:
3-5x \le -9-25x^2 +30x
Questa è una disequazione di secondo grado, quindi portiamo tutto a primo membro.
3-5x +9+25x^2 -30x \le 0
25x^2 -35x +12 \le 0
Calcoliamo il delta:
\Delta = b^2 -4ac = 1225 - 1200 = 25
Delta>0 in una disequazione con minore vuol dire che esiste soluzione e ci andiamo a calcolare le singole soluzioni e poi prenderemo i valori interni.
x_{1,2} = \frac{- b \pm \sqrt{\Delta } }{2a} = \frac{35 \pm 5 }{50}
Ossia:
x_1= \frac{35 + 5 }{50} = \frac{4}{5}
x_2= \frac{35 - 5 }{50} = \frac{3}{5}
Prendiamo i valori interni ed abbiamo concluso l’esercizio!
\frac{3}{5} \le x \le \frac{4}{5}
Abbiamo visto in questa pagina come risolvere disequazioni irrazionali con esercizi svolti!
Sono servite oltre una conoscenza base delle equazioni irrazionali, soprattutto le formule delle disequazioni di secondo grado!
Trovate altre centinaia di esercizi di altri argomenti sia di matematica che altro ancora!
Per approfondire:
https://it.wikipedia.org/wiki/Disequazione_irrazionale
Disequazioni irrazionali esercizi svolti.
irrazionali
esercizi