Disequazioni Logaritmiche ESERCIZI
Disequazioni Logaritmiche ESERCIZI: 15 esercizi svolti! Per la verifica sulle disequazioni logaritmiche basteranno un paio di giorni su questa pagina: a capire e risolvere insieme a noi gli esercizi sulle disequazioni logaritmiche. Prima però è meglio (ma non proprio necessario) che sappiate almeno le basi delle equazioni logaritmiche. Iniziamo subito!
Indice
- Proprietà dei logaritmi
- Disequazioni logaritmiche \log_a b \lessgtr c
- Disequazioni logaritmiche \log_a b \lessgtr \log_a c
- Disequazioni logaritmiche con più logaritmi
- Disequazioni logaritmiche con sostituzione
Per svolgere questi esercizi è fondamentale tenere a portata di mano le proprietà dei logaritmi che useremo tante volte in questa pagina: segnatevele su un foglietto!
Proprietà dei logaritmi

Iniziamo subito con le disequazioni logaritmiche esercizi svolti passo dopo passo!
Disequazioni logaritmiche esercizi
\log_a b \lessgtr c
Esercizio 1. \log_3 (2-5x) > 2
Il PRIMO PUNTO, esattamente come per le equazioni logaritmiche, è la scrittura delle condizioni di esistenza: importantissime perché alla fine dell’esercizio ci diranno se la soluzione va bene o bisogna scartarla! Per i logaritmi, ciò significa porre argomento maggiore di zero.
CE: 2-5x>0 \implies -5x>-2
Cambiamo tutto di segno (nelle disequazioni quando si cambia tutto di segno si cambia anche il segno proprio della disequazione, qui diventa minore per esempio):
CE: 5x<2 \implies x<\frac{2}{5}
Fatto ciò possiamo procedere nella risoluzione dell’esercizio. La disequazione è già nella forma seguente:
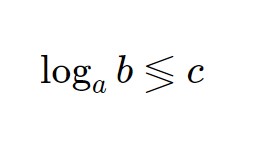
E quindi possiamo applicare la seguente formula che useremo per tutto questo capitolo!
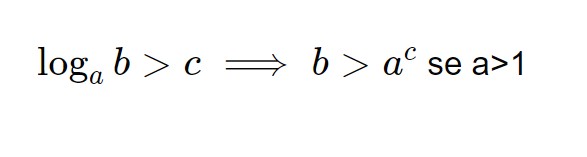
Tale formula ci permetterà di risolvere tutti gli esercizi che si presentano in questo modo, ossia con un solo logaritmo e la presenza di un numero a secondo membro. Come potete vedere tale formula preserva il segno della disequazione SOLAMENTE quando la base del logaritmo è maggiore di 1; negli esercizi successivi vedremo cosa succede quando la base è più piccola.
Torniamo al nostro esercizio, applichiamo la formula ed abbiamo:
\log_3 (2-5x) > 2 \implies 2-5x>3^2
Ossia dobbiamo svolgere una semplice disequazione lineare:
2-5x>9
-5x>7
Cambiamo tutto di segno (e quindi cambiamo anche il segno della disequazione, cioè diventa <):
5x<-7 \implies x< - \frac{7}{5}
Tale soluzione rispetta anche le CE, e quindi va bene, non la scartiamo. L’esercizio è svolto! Questo perchè le CE ci dicono che la x deve essere x<\frac{2}{5} ed infatti questa soluzione lo è!
Esercizio 2. \log_2 (x^2 -1) > 3
Come sempre, e deve diventare una abitudine, scriviamo le condizioni d’esistenza, per i logaritmi significa argomento>0.
CE: x^2-1 > 0 \implies x^2 > 1
Questa la risolviamo facendo la radice ad ambo i membri e prendendo i valori esterni, quindi:
x<-\sqrt{1} \lor x> + \sqrt{1}
CE: x<-1 \lor x> 1
Passiamo all’esercizio ora. Come potete vedere la abbiamo un logaritmo da solo, ed un numero a secondo membro: possiamo applicare quindi già la formula precedente.
\log_2 (x^2 -1) > 3 \implies x^2 -1 > 2^3
Ossia:
x^2 -1 > 8
x^2 > 9
Anche qui come prima, prendiamo le due radici con segno opposto del 9, e poi prendiamo i valori esterni essendoci un maggiore (>):
x<-3 \lor x>3
Tale soluzione rispetta le condizioni di esistenza, e quindi la teniamo così com’è, fatto l’esercizio!
Esercizio 3. \log_{ \frac{1}{3} } (4x-3) > -1
Esercizio IMPORTANTISSIMO!
Partiamo come sempre oramai dalle condizioni di esistenza.
CE: 4x-3>0 \implies x>\frac{3}{4}
A questo punto come potete vedere abbiamo un logaritmo da solo a sinistra, ed un numero a destra, di conseguenza è possibile usare la solita formula. Qui c’è un qualcosa da stare attenti: la base è minore di 1.
Quando la base è più piccola di 1 la formula è sempre la stessa, ma il segno della disequazione viene invertito!
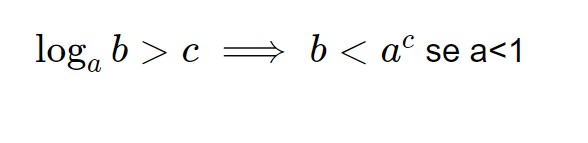
E di conseguenza nel nostro caso da maggiore (>) diventa minore (<):
\log_{ \frac{1}{3} } (4x-3) > -1 \implies 4x-3< (\frac{1}{3})^{-1}
Risolviamola:
4x-3< (\frac{1}{3})^{-1}
Usiamo una proprietà delle potenze: elevato alla -1 significa invertire numeratore e denominatore.
4x-3< 3 \implies 4x<6
E la soluzione è quindi:
x<\frac{3}{2}
A questo punto però intervengono le CE! Perchè le condizioni di esistenza ci dicono che dobbiamo prendere solamente le soluzioni più grandi di \frac{3}{4} , quindi per avere le idee più chiare di cosa prendere, mettiamo tutto a sistema:
\begin{cases} x<\frac{3}{2} \\ x>\frac{3}{4} \end{cases}
Essendo un sistema si prendono gli intervalli in comune, come segue.
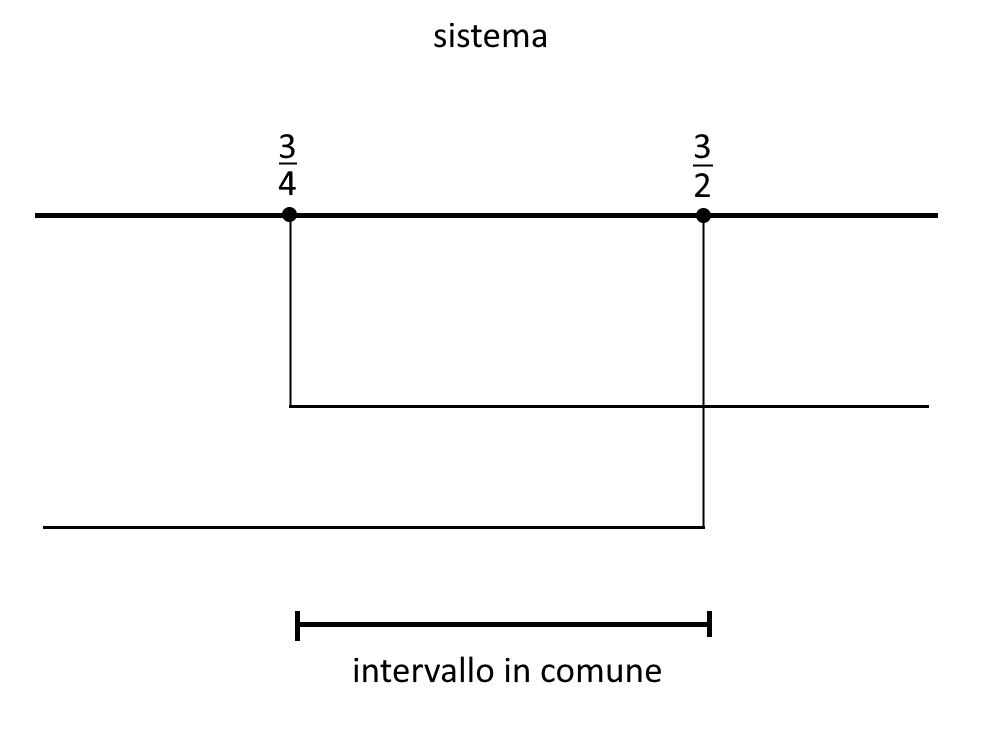
Tale schema lo potete fare sempre per capire meglio quali soluzioni prendere!
Quindi l’intervallo di soluzione è:
\frac{3}{4} < x < \frac{3}{2}
Esercizio 4. 2\log x > 0
Prima cosa?…condizioni di esistenza, esatto!
CE: x>0
A questo punto abbiamo nell’esercizio un numero a destra, e un logaritmo affiancato da un 2. Per applicare la solita formula c’è bisogno che ci sia solamente il logaritmo e nient’altro! Quindi usiamo la terza proprietà dei logaritmi e così ci leviamo da mezzo quel 2.
\log x^2 > 0
Ora la disequazione è nella forma giusta, utilizziamo la formula.
\log x^2 > 0 \implies x^2 > 10^0
E quindi:
x^2 > 1
Essendoci un maggiore prendiamo i valori esterni delle due radici con segno opposto:
x<-1 \lor x> 1
A causa delle CE, che ci dicono che la soluzione deve essere maggiore di zero, allora scartiamo la prima parte e prendiamo solo la seconda. Quindi solo x>1 !
Continuiamo con altre disequazioni logaritmiche esercizi svolti!
Disequazioni logaritmiche esercizi
\log_a b \lessgtr \log_a c
Esercizio 5. \log_5 ( \frac{2-x}{x+3} ) < \log_5 4
Partiamo dalle condizioni di esistenza che a volte, come in questo caso, è un po’ lunghetto da risolvere.
CE: \frac{2-x}{x+3} > 0
Questa è un disequazione fratta, che si risolve con un falso sistema.
\big\| 2-x>0 \\ \big\| x+3>0
\big\| x<2 \\ \big\| x>-3
A questo punto, essendo un falso sistema vediamo il quadro dei segni.
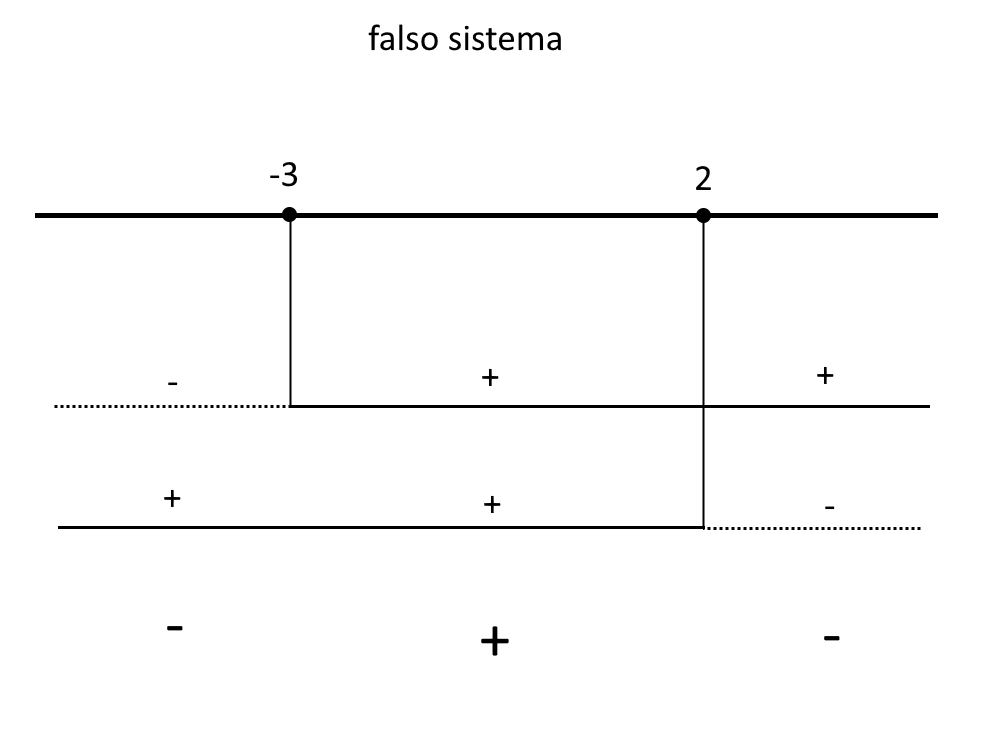
Essendo che nella disequazione iniziale c’è un maggiore, prendiamo l’intervallo col segno +, quindi:
CE: -3<x<2
Ora possiamo procedere con l’esercizio. Questo è un nuovo caso: quando abbiamo un solo logaritmo a sinistra ed uno solo a destra, applichiamo adesso quest’altra importante formula!
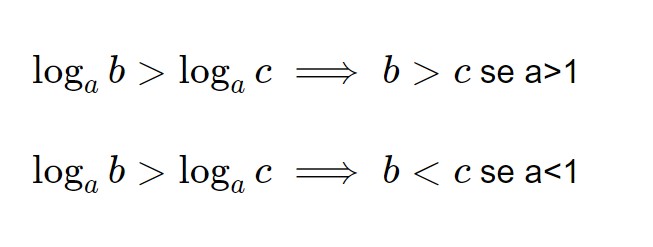
Per il nostro esercizio:
\log_5 ( \frac{2-x}{x+3} ) < \log_5 4
\implies \frac{2-x}{x+3} < 4
In pratica i logaritmi è come se scomparissero.
Abbiamo ancora una volta una disequazione fratta, che se non vi ricordate come si risolvono, cliccateci sopra e capite giusto in un paio di esercizi. Comunque, dobbiamo portare il 4 a primo membro:
\frac{2-x}{x+3} - 4 <0
Facciamo il minimo comune multiplo:
\frac{ 2-x-4(x+3) }{x+3} <0
\frac{ 2-x-4x -12 }{x+3} <0
Sommiamo i rispettivi termini simili:
\frac{ -5x -10 }{x+3} <0
Ed adesso siamo nelle condizioni di risolvere questa disequazione, con un falso sistema, come prima.
\big\| -5x -10 < 0 \\ \big\| x+3<0
Questa volta col segno < perché il falso sistema conserva il segno della disequazione.
\big\| x > -2 \\ \big\| x<-3
Prendendo gli intervalli col segno –, ossia:
x<-3 \lor x>-2
Adesso uniamo questa soluzione con le CE in un sistema per vedere cosa tenere e cosa scartare.
\begin{cases} x<-3 \lor x>-2 \\ -3<x<2 \end{cases}
Ed essendo un sistema prendiamo gli intervalli comuni.
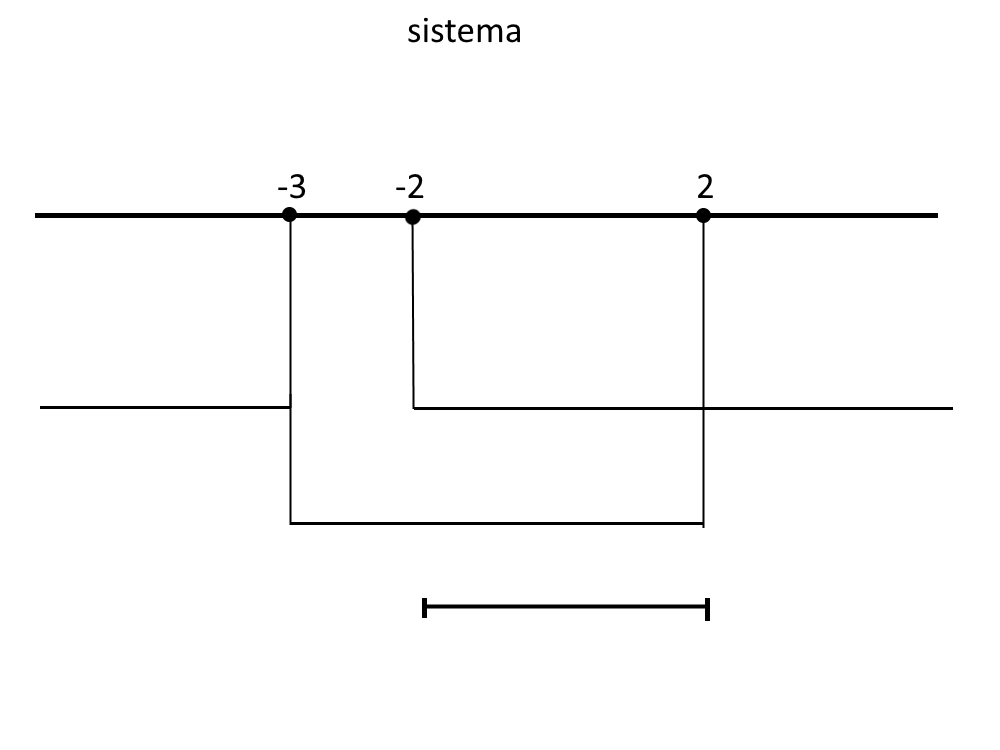
E quindi notiamo che bisogna prendere come soluzione:
-2<x<2
Esercizio 6. \log (2x - x^2 ) < \log ( x -2 )
Quando le CE da calcolare sono più di una si scrive tutto in un sistema, e si prende alla fine gli intervalli comuni, al fine di avere una unica condizione d’esistenza.
CE: \begin{cases} 2x-x^2 >0 \\ x-2>0 \end{cases}
CE: \begin{cases} x(2-x) > 0 \\ x>2 \end{cases}
Dopo aver messo in evidenza una x calcoliamo questa CE del primo logaritmo con un falso sistema scritto da parte.
\big\| x>0 \\ \big\| 2-x>0
\big\| x>0 \\ \big\| x<2
E dal quadro dei segni ricaviamo che, prendendo l’intervallo positivo:
0<x<2
E questa era la prima CE, sostituiamola nel sistema.
CE:\begin{cases} 0<x<2 \\ x>2 \end{cases}
Essendo che nel sistema si prendono le soluzioni comuni, qui non ce ne sono.
E quindi CE: \nexists x
Le condizioni di esistenza ci dicono che tale disequazione non permette nessuna x come soluzione. Quindi non c’è bisogno di fare l’esercizio: qualsiasi soluzione la scarteremmo! Quindi la disequazione è impossibile o non ha soluzione!
Ecco quindi un altro esempio del perchè le CE sono straimportanti!
Esercizio 7. \log_{ \frac{1}{10} } ( \frac{x+1}{x-1} ) > \log_{ \frac{1}{10} } ( \frac{x}{x+1} )
Partiamo con le condizioni di esistenza, che saranno un po’ lunghette questa volta (ma se fatte bene son già punti preziosi per la verifica in classe!).
Qui abbiamo sia logaritmi che frazioni, quindi andiamo a porre anche le CE delle frazioni, ossia denominatori diversi da zero.
CE: \begin{cases} \frac{x+1}{x-1} >0 \\ \frac{x}{x+1} >0 \\ x-1 \ne 0 \\ x+1 \ne 0 \end{cases}
CE: \begin{cases} \frac{x+1}{x-1} >0 \\ \frac{x}{x+1} >0 \\ x \ne 1 \\ x \ne -1 \end{cases}
Prendiamo da parte il primo logaritmo del sistema.
\frac{x+1}{x-1} >0
Che, come prima, risolviamo grazie ad un falso sistema.
\big\| x+1>0 \\ \big\| x-1>0
\big\| x>-1 \\ \big\| x>1
Prendiamo nel quadro dei segni gli intervalli col segno +, ossia:
x<-1 \lor x> 1
Adesso passiamo al secondo logaritmo del sistema.
\frac{x}{x+1} >0
Anche questa volta andiamo a risolvere un altro falso sistema.
\big\| x>0 \\ \big\| x+1>0
\big\| x>0 \\ \big\| x>-1
Prendiamo gli intervalli col segno +, ossia:
x<-1 \lor x>0
Sostituiamo questo risultato e quello del primo logaritmo nel sistema:
CE: \begin{cases}x<-1 \lor x> 1 \\ x<-1 \lor x>0 \\ x \ne 1 \\ x \ne -1 \end{cases}
Mettiamo queste informazioni in uno schema, e prendiamo gli intervalli comuni di soluzioni.
x<-1 \lor x>1
(Ricordate che ogni rigo del sistema va messo su una singola linea dello schema, come vedete nella figura sopra)
ADESSO passiamo finalmente alla risoluzione dell’esercizio!
La disequazione dell’esercizio già è nella forma adatta per applicare la formula, ossia mettere in disuguaglianza gli argomenti.
Attenzione che qui la base è minore di 1 dei logaritmi, e quindi bisogna invertire il segno!
\frac{x+1}{x-1} < \frac{x}{x+1}
Come vedete, essendo il logaritmo in base minore di 1, è diventato da maggiore un minore!
Abbiamo adesso una disequazione fratta. Quindi portiamo tutto a primo membro:
\frac{x+1}{x-1} - \frac{x}{x+1} < 0
Facciamo un minimo comune multiplo per compattare il tutto.
\frac{ (x+1)(x+1) - x(x-1) }{ (x-1)(x+1) } < 0
\frac{ x^2 +1 +2x - x^2 +x }{ (x-1)(x+1) } < 0
Sommiamo i termini comuni:
\frac{ 3x+1 }{ (x-1)(x+1) } < 0
E risolviamo questo con un falso sistema come sempre quando si parla di disequazione.
\big\| 3x+1 < 0 \\ \big\| (x-1)(x+1) < 0
A questo punto abbiamo a primo termine una semplice disequazione, e a secondo termine un prodotto. Per il primo non ci sono problemi:
\big\| x< - \frac{1}{3} \\ \big\| (x-1)(x+1) < 0
Il secondo lo risolviamo da parte, con un altro falso sistema.
\big\| x-1 < 0 \\ \big\| x+1 < 0
\big\| x < 1 \\ \big\| x < -1
Prendiamo l’intervallo col segno –, ossia:
-1<x<1
Sostituiamo nel falso sistema iniziale ed andiamo a concludere l’esercizio:
\big\| x< - \frac{1}{3} \\ \big\| -1<x<1
E prendiamo:
x<-1 \lor -\frac{1}{3} < x < 1
Ora è il momento di vedere se tale soluzione va bene: mettiamola a sistema con le CE.
\begin{cases}x<-1 \lor -\frac{1}{3} < x < 1 \\ x<-1 \lor x>1 \end{cases}
Ci accorgiamo che, prendendo solo gli intervalli comuni nel solito schema la soluzione è solo x<-1.
Esercizio 8. \log_{ \frac{4}{5} } ( 2-x^2 ) - \log_{ \frac{4}{5} } ( 1-2x ) < 0
Facciamo le condizioni di esistenza di tutte e due gli argomenti:
CE: \begin{cases} 2-x^2 > 0 \\ 1-2x >0 \end{cases}
CE: \begin{cases} -x^2 > -2 \\ -2x >-1 \end{cases}
Cambiamo di segno a tutte e due, ed al secondo dividiamo per 2.
CE: \begin{cases} x^2 < 2 \\ x < \frac{1}{2} \end{cases}
Il primo, si risolve prendendo le due radici con segno opposto, e prendendo i valori interni essendoci un minore.
CE: \begin{cases} -\sqrt{2} < x < \sqrt{2} \\ x < \frac{1}{2} \end{cases}
Prendiamo gli intervalli comuni, ossia:
-\sqrt{2} < x < \frac{1}{2}
Passiamo alla risoluzione dell’esercizio. Portiamo a secondo membro l’altro logaritmo.
\log_{ \frac{4}{5} } ( 2-x^2 ) < \log_{ \frac{4}{5} } ( 1-2x )
E siamo nelle condizioni di applicare la formula! Invertiamo il segno essendo la base minore di 1.
2-x^2 > 1-2x
Abbiamo una disequazione di secondo grado, portiamo quindi tutto a primo membro:
2-x^2 -1+2x > 0
-x^2 +1+2x > 0
Cambiamo tutto di segno e riordiniamola:
x^2 -2x -1 < 0
Calcoliamo il discriminante:
\frac{\Delta}{4} = (\frac{b}{2})^2 -4ac = 1+1 = 2
Delta>0 e quindi esiste soluzione. Calcoliamo quindi le singole soluzioni, e poi prendiamone i valori interni (essendo la disequazione col segno di minore).
x_{1,2} = \frac{- \frac{b}{2} \pm \sqrt{ \frac{\Delta}{4} }}{a} = \frac{1 \pm \sqrt{2} }{1}
E quindi:
x_1 = 1-\sqrt{2}
x_2 = 1+\sqrt{2}
E poi prendiamo i valori interni:
1-\sqrt{2} <x< 1+\sqrt{2}
Adesso le CE intervengono e dobbiamo scartare una parte della soluzione, mettiamo a sistema quindi CE con la soluzione:
\begin{cases} 1-\sqrt{2} <x< 1+\sqrt{2} \\ -\sqrt{2} < x < \frac{1}{2} \end{cases}
Prendiamo:
1-\sqrt{2} <x < \frac{1}{2}
Continuiamo con altre disequazioni logaritmiche esercizi svolti!
Disequazioni logaritmiche con più logaritmi
Esercizio 9. \log_{ \frac{1}{4} } ( x^2 -6 ) - \log_{ \frac{1}{4} } ( x-3 ) > -1
Iniziamo dalle condizioni di esistenza, come vedete solo dei due logaritmi.
CE: \begin{cases} x^2 -6 > 0 \\ x-3>0 \end{cases}
CE: \begin{cases} x^2 > 6 \\ x>3 \end{cases}
Il primo termine prendiamo le due radici con segno opposto, e poi i loro valori esterni essendoci un maggiore.
CE: \begin{cases} x<-\sqrt{6} \lor x>\sqrt{6} \\ x>3 \end{cases}
Prendiamo gli intervalli comuni, con il solito schema, ossia:
CE: x>3
Passiamo allo svolgimento dell’esercizio!
Qui abbiamo due logaritmi ed un ulteriore termine. Quando i termini sono più di due bisogna sempre applicare le prime due proprietà dei logaritmi. In questo caso essendoci un meno fra i due logaritmi, applichiamo la seconda per ridurre il numero di logaritmi.
\log_{ \frac{1}{4} } ( \frac{x^2 -6}{x-3} ) > -1
E’ comparsa una frazione per la quale la sua CE è già compresa nelle nostre, non dobbiamo fare null’altro.
Adesso abbiamo un logaritmo ed un numero a secondo membro: ci siamo ricondotti al primo caso. Quindi applichiamo la formula per passare ad un esponenziale (ricordandoci di cambiare il segno della disequazione essendo la base minore di 1):
\implies \frac{x^2 -6}{x-3} < (\frac{1}{4})^{-1}
\frac{x^2 -6}{x-3} < 4
Abbiamo una disequazione fratta: portiamo a primo membro tutto e facciamo il minimo comune multiplo.
\frac{x^2 -6}{x-3} - 4 < 0
\frac{x^2 -6 - 4(x-3) }{x-3} < 0
Sciogliamo la parentesi e sommiamo i termini rispettivi.
\frac{x^2 - 4x + 6 }{x-3} < 0
Risolviamo con un falso sistema questa disequazione (ricordate che nel falso sistema i segni sono quelli della disequazione).
\big\| x^2 - 4x + 6 < 0 \\ \big\| x -3 < 0
Il secondo termine è semplice:
\big\| x^2 - 4x + 6 < 0 \\ \big\| x < 3
Il primo, che è una disequazione di secondo grado la risolviamo da parte, calcolando il delta-quarti:
\frac{\Delta}{4} = (\frac{b}{2})^2 -4ac = 4+6 = -2
Delta<0 con una disequazione col minore significa che non esiste soluzione. Sostituiamo nel falso sistema:
\big\| \nexists x \\ \big\| x < 3
Il primo termine si indica con una linea tratteggiata, che indica un segno – nel quadro dei segni.
Prendiamo l’intervallo col segno –, quindi: x<3
Ma le CE ci indicano il contrario, quindi non esiste soluzione! Di fatti:
\begin{cases} x<3 \\ x>3 \end{cases}
No soluzione!
Esercizio 10. 2 \log_{ \sqrt{3} } ( 1-x ) - \log_{ \sqrt{3} } ( 3-x ) < 2
Scriviamo le condizioni di esistenza dei due logaritmi:
CE: \begin{cases} 1-x >0 \\ 3-x>0 \end{cases}
CE: \begin{cases} -x >-1 \\ -x>-3 \end{cases}
Cambiamo di segno tutto (anche il segno delle disequazioni, non dimenticatelo).
CE: \begin{cases} x < 1 \\ x<3 \end{cases}
Prendiamo come intervallo comune:
CE: x<1
Passiamo a risolvere l’esercizio. Iniziamo a scrivere il 2 come logaritmo:
2= 2 \cdotp 1 = 2 \log_{ \sqrt{3} } \sqrt{3}
E poi usando la terza proprietà dei logaritmi portiamo il 2 dentro al logaritmo.
= \log_{ \sqrt{3} } (\sqrt{3})^2 =\log_{ \sqrt{3} } 3
Facciamo lo stesso anche col primo termine dell’esercizio: ossia portiamo il 2 dentro. Così facendo abbiamo tutti logaritmi, e siamo nelle condizioni di applicare le prime due proprietà dei logaritmi (che come potete vedere non c’è la presenza di altri numeri al di fuori dei logaritmi).
\log_{ \sqrt{3} } ( 1-x )^2 - \log_{ \sqrt{3} } ( 3-x ) < \log_{ \sqrt{3} } 3
Applichiamo per la precisione la seconda proprietà ai primi due termini:
\log_{ \sqrt{3} } \frac{( 1-x )^2}{3-x} < \log_{ \sqrt{3} } 3
Ora, siamo nel caso precedente: logaritmo da solo a sinistra ed uno a destra. Quindi mettiamo gli argomenti in disuguaglianza:
\frac{( 1-x )^2}{3-x} < 3
Abbiamo una disequazione fratta, quindi:
\frac{( 1-x )^2}{3-x} - 3 < 0
Facciamo il mcm:
\frac{( 1-x )^2 - 3(3-x ) }{3-x} < 0
\frac{1+x^2 -2x - 9+3x }{3-x} < 0
Sommiamo i termini corrispettivi al numeratore:
\frac{x^2 +x - 8 }{3-x} < 0
E risolviamo questo con un falso sistema.
\big\| x^2 +x - 8 < 0 \\ \big\| 3-x < 0
\big\| x^2 +x - 8 < 0 \\ \big\| x > 3
La prima è una disequazione di secondo grado, calcoliamo il delta:
\Delta = b^2 - 4ac = 1+32 = 33
Calcoliamo le singole soluzioni, e poi visto il minore della disequazione, prendiamo i valori interni.
x_{1,2} = \frac{- b \pm \sqrt{ \Delta }}{2a} = \frac{-1 \pm \sqrt{33} }{2}
Quindi:
x_1 = \frac{-1 + \sqrt{33} }{2}
x_1 = \frac{-1 - \sqrt{33} }{2}
E, come detto, prendiamo i valori interni:
\frac{-1 - \sqrt{33} }{2} <x< \frac{-1 + \sqrt{33} }{2}
Ora, mettiamo a sistema la soluzione con le CE, ed il gioco è fatto!
\begin{cases} \frac{-1 - \sqrt{33} }{2} <x< \frac{-1 + \sqrt{33} }{2} \\ x<1 \end{cases}
E quindi la soluzione finale è:
\frac{-1 - \sqrt{33} }{2} <x< 1
Esercizio 11. \log ( x+5 ) - \log ( 4-x ) + \log ( 3x-1 ) > \log ( 3x-1 ) - \log ( x+4 )
Qui le condizioni di esistenza sono ben 5!
CE: \begin{cases} x+5>0 \\ 4-x>0 \\ 3x-1>0 \\ 3x-1>0 \\ x+4>0 \end{cases}
CE: \begin{cases} x>-5 \\ x<4 \\ x>\frac{1}{3} \\ x>\frac{1}{3} \\ x>-4 \end{cases}
L’intervallo di CE comune è:
\frac{1}{3} < x < 4
Possiamo notare che nell’esercizio il termine \log (3x-1) si leva, perchè ne abbiamo uno a sinistra ed uno a destra.
\log ( x+5 ) - \log ( 4-x ) > - \log ( x+4 )
Ai primi due termini applichiamo la seconda proprietà, a secondo membro applichiamo la terza proprietà.
\log \frac{ x+5 }{4-x} > \log ( x+4 )^{-1}
Scriviamo per comodità in frazione il secondo termine:
\log \frac{ x+5 }{4-x} > \log \frac{ 1 }{x+4}
Abbiamo un logaritmo a sinistra ed uno a destra, quindi siamo nel caso precedente ed applichiamo la solita formula:
\frac{ x+5 }{4-x} > \frac{ 1 }{x+4}
Ancora una volta una disequazione fratta.
\frac{ x+5 }{4-x} - \frac{ 1 }{x+4} > 0
mcm:
\frac{ (x+5)(x+4) - (4-x) }{ (4-x)(x+4) } > 0
\frac{ x^2 + 4x+5x+ 20 - 4+x }{ (4-x)(x+4) } > 0
Sommiamo i rispettivi termini:
\frac{ x^2 + 10x+ 16}{ (4-x)(x+4) } > 0
Questo lo risolve con un falso sistema.
\big\| x^2 + 10x+ 16 > 0 \\ \big\| (4-x)(x+4) > 0
Calcoliamo da parte il primo termine, che è una disequazione di secondo grado. Il discriminante è:
\frac{\Delta}{4} = (\frac{b}{2})^2 -ac = 25-16 = 9
E le due soluzioni singole le calcoliamo da:
x_{1,2} = \frac{- \frac{b}{2} \pm \sqrt{ \frac{\Delta}{4} }}{a} = \frac{-5 \pm 3 }{1}
Ed allora:
x_1 = -5-3=-8
x_2 = -5+3=-2
Poiché abbiamo un maggiore nella disequazione di secondo grado, si prendono i valori esterni di queste due soluzioni:
x<-8 \lor x>-2
Passiamo adesso al secondo termine del falso sistema. Che a sua volta risolviamo con un altro falso sistema ancora.
\big\| 4-x > 0 \\ \big\| x+4 > 0
\big\| x < 4 \\ \big\| x > -4
Prendiamo l’intervallo col segno +, visto che c’è un maggiore nella disequazione, ed allora:
-4<x<4
Sostituiamo il tutto nel falso sistema iniziale finalmente:
\big\| x<-8 \lor x>-2 \\ \big\| -4<x<4
Prendiamo gli intervalli positivi:
-8<x<-4 \lor -2<x<4
Adesso prima di concludere l’esercizio, dobbiamo verificare se tali soluzioni vanno bene. Cioè mettiamo a sistema le soluzioni con le CE.
\begin{cases} -8<x<-4 \lor -2<x<4 \\ \frac{1}{3} < x < 4 \end{cases}
La soluzione finale è quindi:
\frac{1}{3} < x < 4
Esercizio 12. \log ( 2+\frac{1}{x} ) - \log ( 2-\frac{1}{x} ) < \log ( 2x+1 ) - \log ( 1-2x )
Iniziamo come sempre dalle CE dei 4 logaritmi qui, inoltre bisogna anche mettere quello delle frazioni, ossia denominatore diverso da zero!
CE: \begin{cases} 2+\frac{1}{x} >0 \\ 2-\frac{1}{x}>0 \\ 2x+1 > 0 \\ 1-2x>0 \\ x \ne 0 \end{cases}
Moltiplichiamo per x ai primi due termini.
CE: \begin{cases} 2x+1 >0 \\ 2x-1>0 \\ 2x+1 > 0 \\ 1-2x>0 \\ x \ne 0 \end{cases}
2x+1 compare due volte, lo scriviamo una sola.
CE: \begin{cases} x >-\frac{1}{2} \\ x>\frac{1}{2} \\ x<\frac{1}{2} \\ x \ne 0 \end{cases}
E troviamo che non esiste un intervallo in comune a tutti. Quindi le CE ci stanno dicendo che qualsiasi x la dovremo scartare. L’esercizio finisce già qui, perchè non ci sarà soluzione!
Continuiamo con altre disequazioni logaritmiche esercizi svolti!
Disequazioni logaritmiche esercizi con sostituzione
Esercizio 13. ( \log x )^2 - 7 \log x +12 < 0
Quando abbiamo logaritmi elevati al quadrato deve subito scattare alla mente l’idea di poter effettuare una sostituzione. Ricordatevi che il seguente non è un logaritmo quadro, il seguente è solo un argomento elevato al quadrato:
\log x^2
Ma lo è il seguente:
\log^2 x
Oppure questo:
(\log x)^2 = \log^2 x
Fatta questa piccola parentesi, incominciamo!
CE: x>0
In questa equazione abbiamo: due logaritmi con stessa base e stesso argomento, ed inoltre il primo è al quadrato, quindi possiamo effettuare una sostituzione! Questa evidenziate sono infatti le premesse per far sì che si possa fare una sostituzione. Poniamo infatti:
\log x = t
Quindi l’equazione nella nuova variabile diventa:
t^2 - 7 t +12 < 0
Siamo passati dai logaritmi ad una disequazione di secondo grado! Troviamo il delta:
\Delta = b^2 - 4ac = 49-48 = 1
Delta>0 quindi esiste soluzione, troviamole e poi andiamo a prendere i valori interni, essendoci un minore nella disequazione.
t_{1,2} = \frac{- b \pm \sqrt{ \Delta }}{2a} = \frac{7 \pm 1 }{2}
Ossia:
t_1 = \frac{7 + 1 }{2}=4
t_2 = \frac{7 - 1 }{2}= 3
Prendiamo i valori interni:
3<t<4
Ritorniamo adesso alla variabile x iniziale:
3< \log x <4
Quando vedete un qualcosa del genere (con valori compresi) lo si spezza in due separate disequazioni, messe a sistema.
\begin{cases}3< \log x \\ \log x <4 \end{cases}
\begin{cases} \log x > 3 \\ \log x <4 \end{cases}
Esse sono logaritmi del primo capitolo di questa pagina, quindi usiamo la formula per passare agli esponenziali!
\begin{cases} x > 10^3 \\ x <10^4 \end{cases}
Essendo un sistema, si prendono i valori comuni, quindi la soluzione è:
10^3 < x < 10^4
Esercizio 15. [\log_2 ( x+5 ) ]^2 - \log_2 ( x+5 ) -6 > 0
CE: x+5>0 cioè x>-5
Abbiamo: logaritmi con stessa base, e con stesso argomento; inoltre il primo è elevato al quadrato. Abbiamo quindi tutte le condizioni per procedere per sostituzione. Poniamo:
\log_2 (x+5) = t
L’equazione diventa:
t^2 - t -6 > 0
Calcoliamo il discriminante.
\Delta = b^2 - 4ac = 1+24 = 25
Delta>0 quindi esiste soluzione, troviamole e poi andiamo a prendere i valori esterni, poiché vi è un maggiore.
t_{1,2} = \frac{- b \pm \sqrt{ \Delta }}{2a} = \frac{1 \pm 5 }{2}
Cioè:
t_1 = \frac{1 + 5 }{2} = 3
t_2 = \frac{1 - 5 }{2}=-2
Prendiamo i valori esterni:
t<-2 \lor t>3
Ritorniamo alla variabile x:
\log_2 (x+5) < -2 \lor \log_2 (x+5) > 3
Trattiamo invece i valori esterni separatamente:
\log_2 (x+5) < -2 \\ \log_2 (x+5) > 3
Usiamo la solita formula per passare agli esponenziali:
(x+5) < 2^{-2} \\ (x+5) > 2^3
x < \frac{1}{4}-5 \\ x > 8-5
E troviamo:
x <- \frac{19}{4} \\ x > 3
A questo punto prendiamo queste due soluzioni e mettiamole a sistema con le CE per vedere cosa tenere e cosa scartare.
\begin{cases} x <- \frac{19}{4} \lor x > 3 \\ x>-5 \end{cases}
E quindi:
-5<x<- \frac{19}{4} \lor x > 3
In questa pagina abbiamo visto come svolgere esercizi sulle disequazioni logaritmiche. Per la preparazione al compito è necessaria una ripetizione, almeno delle formule, delle disequazioni fratte e delle disequazioni di secondo grado.
L’argomento precedente sono le equazioni logaritmiche. Trovate inoltre altre centinaia di esercizi su questo sito di tanti altri argomenti di matematica che altro ancora!
Per approfondire:
https://it.wikipedia.org/wiki/Disequazione_logaritmica
Disequazioni logaritmiche esercizi.
logaritmiche
esercizi