Esercizi Disequazioni FRATTE
Esercizi Disequazioni FRATTE: 15 ESERCIZI SVOLTI! In questa pagina mostreremo esercizi sulle disequazioni di primo grado fratte e quelle di secondo grado fratte: sarete pronti per il compito in men che non si dica! Ci saranno 15 esercizi spiegati con calma e in ogni singolo passaggio. Prima è importante però che sappiate come funzionano le equazioni fratte. Comunque partiamo subito!
Indice
- Disequazioni fratte di primo grado
- Disequazioni fratte di secondo grado
- Disequazioni fratte di grado superiore al secondo
Iniziamo subito con gli esercizi disequazioni fratte di primo grado!
Esercizi disequazioni fratte di primo grado
Esercizio 1. \frac{x-7}{x+3} < 0
La prima cosa da fare è sicuramente trovare le condizioni di esistenza. Qui abbiamo una frazione e di conseguenza poniamo denominatore diverso da zero.
CE: x+3 \ne 0 \implies x \ne -3
Dopo aver calcolato le condizioni di esistenza, possiamo passare alla risoluzione della disequazione fratta. Una volta che abbiamo la forma seguente:
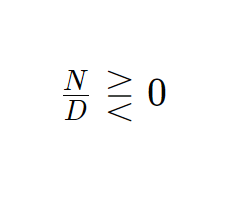
Possiamo risolvere la disequazione con un falso sistema. Cioè risolviamo separatamente numeratore e denominatore con lo stesso segno della disequazione, nel modo seguente:
\big\| x-7 <0 \\ \big\| x+3 < 0
Isoliamo la x, e portiamo i numeri nel secondo membro, ricordandoci di cambiare di segno i numeri.
\big\| x < 7 \\ \big\| x < -3
A questo punto i giochi sono fatti. Disegniamo un grafico dei segni, nel modo seguente. Disegniamo una pallina vuota nei numeri che non vanno presi, visto che non c’è l’uguale anche.
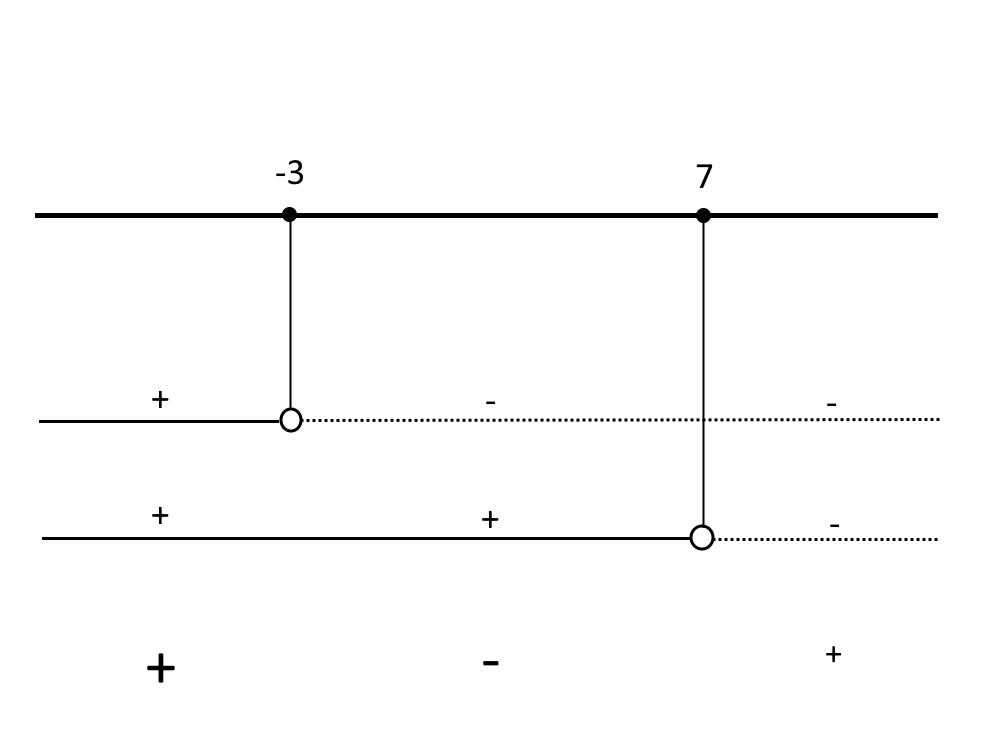
Ad ogni linea piena gli associamo un segno +. Ad ogni linea tratteggiata gli associamo un segno –. Giù andiamo a calcolare il segno finale, facendo la regola dei segni: quindi + per + fa +, – per – fa +, + per – fa -.
La nostra disequazione dell’esercizio ha un segno di minore (<), e quindi andiamo a prendere come soluzioni tutti gli intervalli con un segno – nel grafico dei segni! Quindi:
-3 < x < 7
Non serve escludere nessuna soluzione per le CE, visto che x=-3 già è compresa.
Ricordate che x<3 significa prendere tutti i valori più piccoli di 3, ma NON uguali a 3 !
Esercizio 2. \frac{1-x}{2x-3} > 1
La prima cosa da fare come sempre, in tutte le equazioni e disequazioni è il calcolo delle CE.
CE: 2x-3 \ne 0 \implies 2x \ne 3
\implies x \ne \frac{3}{2}
Perchè sono importanti le CE? Perchè ci permettono alla fine dell’esercizio di escludere, se ci sono, eventuali soluzioni!
Ritorniamo all’esercizio. Visto che la disequazione non è della forma:
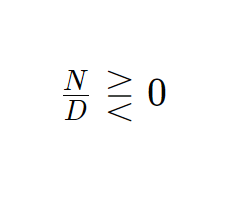
Dobbiamo prima portare l’1 a primo membro.
\frac{1-x}{2x-3} - 1 > 0
E poi facciamo il minimo comune multiplo per avere un solo denominatore ed un solo numeratore:
\frac{1-x - (2x-3 )}{2x-3} > 0
Sciogliamo la parentesi.
\frac{1-x - 2x+3 }{2x-3} > 0
Sommiamo i termini comuni:
\frac{4-3x }{2x-3} > 0
A questo punto e solo a questo punto andiamo a risolvere la disequazione con un falso sistema! Qui bisogna mettere un segno di maggiore (>) cioè lo stesso segno della disequazione dell’esercizio
\big\|4-3x > 0 \\ \big\| 2x-3 > 0
Isoliamo la x e portiamo il termine noto a secondo membro.
\big\|-3x > -4 \\ \big\| 2x > 3
A questo punto, nella prima disequazione bisogna cambiare tutto di segno e poi dividere tutto per 3. Quando fate un cambio di segno in una disequazione bisogna anche cambiare il segno della disequazione: quindi lì diventerà un minore (<)!
\big\|3x < 4 \\ \big\| 2x > 3
\big\|x < \frac{4}{3} \\ \big\| x > \frac{3}{2}
Ora, bisogna riportare questi dati su una tabella dei segni.
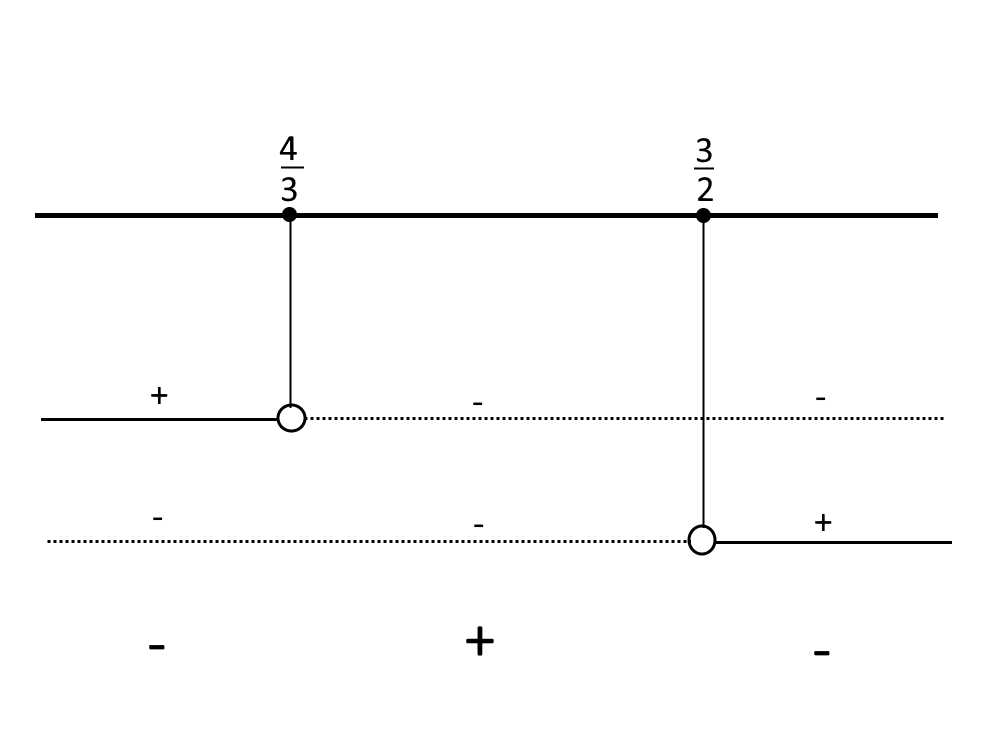
E come detto nell’esercizio precedente, dobbiamo prendere come intervalli di soluzione quelli con stesso segno della disequazione. Nel nostro caso abbiamo un maggiore (>) e quindi prendiamo gli intervalli col +. Quindi:
\frac{4}{3} < x < \frac{3}{2}
La CE è già inclusa in questo caso e quindi non dobbiamo fare nient’altro! Abbiamo concluso l’esercizio!
Esercizio 3. \frac{3x}{x-2} \ge 1
Il procedimento è sempre lo stesso: calcoliamo innanzitutto le CE.
CE: x-2 \ne 0 \implies x \ne 2
Ora prima di procedere col falso sistema, portiamo l’1 a primo membro.
\frac{3x}{x-2} -1 \ge 0
E poi facciamo il minimo comune multiplo per avere un unico numeratore e un unico denominatore.
\frac{3x - (x-2) }{x-2} \ge 0
\frac{3x - x+2 }{x-2} \ge 0
Sommiamo i termini:
\frac{2x +2 }{x-2} \ge 0
Ora possiamo finalmente al calcolo del falso sistema. Attenzione qui! Quando avete un segno di \ge, \le alla disequazione cui corrisponde il denominatore non va messo l’uguale! Questo perchè la CE ve lo vieta! Quindi:
\big\| 2x +2 \ge 0 \\ \big\| x-2 > 0
Isoliamo la x e risolviamo le singole!
\big\| 2x \ge -2 \\ \big\| x > 2
\big\| x \ge -1 \\ \big\| x > 2
Poi passiamo alla tabella dei segni. Questa volta andiamo a riempire il cerchio in corrispondenza della x=-1, perchè quel valore è compreso.
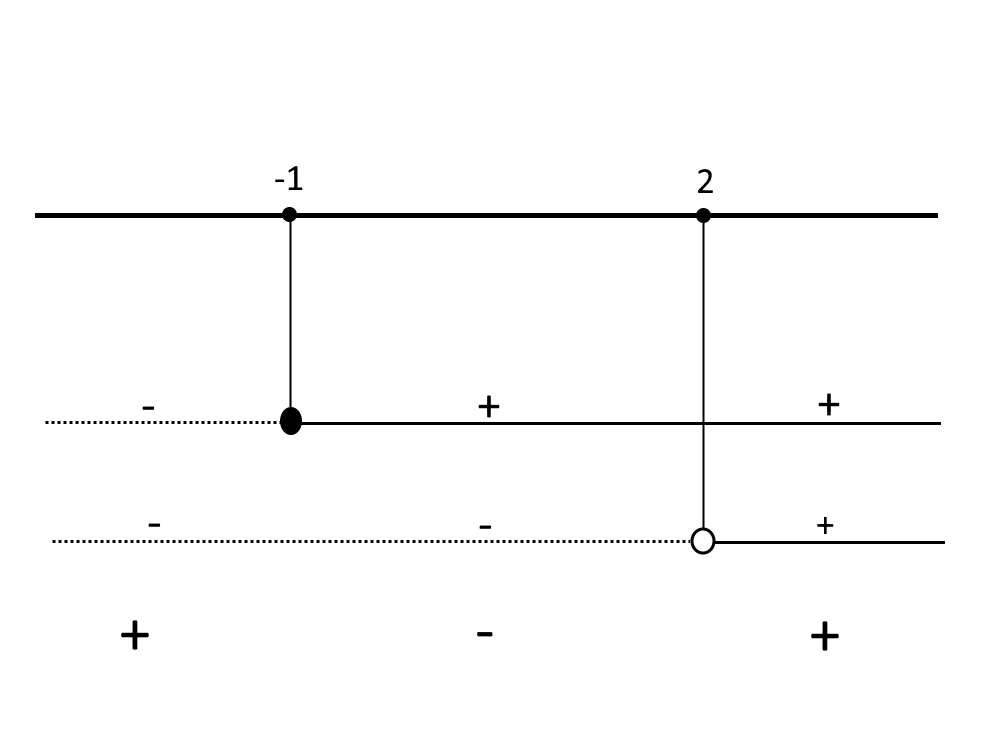
Prendiamo i valori positivi, visto che la disequazione ha un segno di maggiore o uguale. Attenzione qui ad osservare bene cosa comprendere e cosa no! Abbiamo come soluzione:
x<-1 \lor x > 2
Anche qui le CE sono già comprese!
Continuiamo con altri esercizi disequazioni fratte di primo grado!
Esercizio 4. \frac{x}{x-5} \le 3
Calcoliamo le condizioni di esistenza, non dimenticatevele mai! Perchè vedrete che in certi esercizi saranno utili!
CE: x-5 \ne 0 \implies x \ne 5
Ora passiamo il 3 a primo membro.
\frac{x}{x-5} - 3 \le 0
E facciamo il minimo comune multiplo:
\frac{x - 3 (x-5)}{x-5} \le 0
Svolgiamo la parentesi attenti anche a cambiare il secondo segno.
\frac{x - 3x +15)}{x-5} \le 0
\frac{-2x +15)}{x-5} \le 0
Passiamo a questo punto, ossia quando avete un numeratore e denominatore già compatti, a fare un falso sistema.
\big\| -2x +15 \le 0 \\ \big\| x-5 < 0
Ricordatevi sempre di non mettere l’uguale alla seconda disequazione, per via delle CE.
\big\| -2x \le -15 \\ \big\| x < 5
Cambiamo di segno alla prima (ricordatevi che poi diventa un maggiore uguale).
\big\| x \ge \frac{15}{2} \\ \big\| x < 5
Ora passiamo alla tabella dei segni.
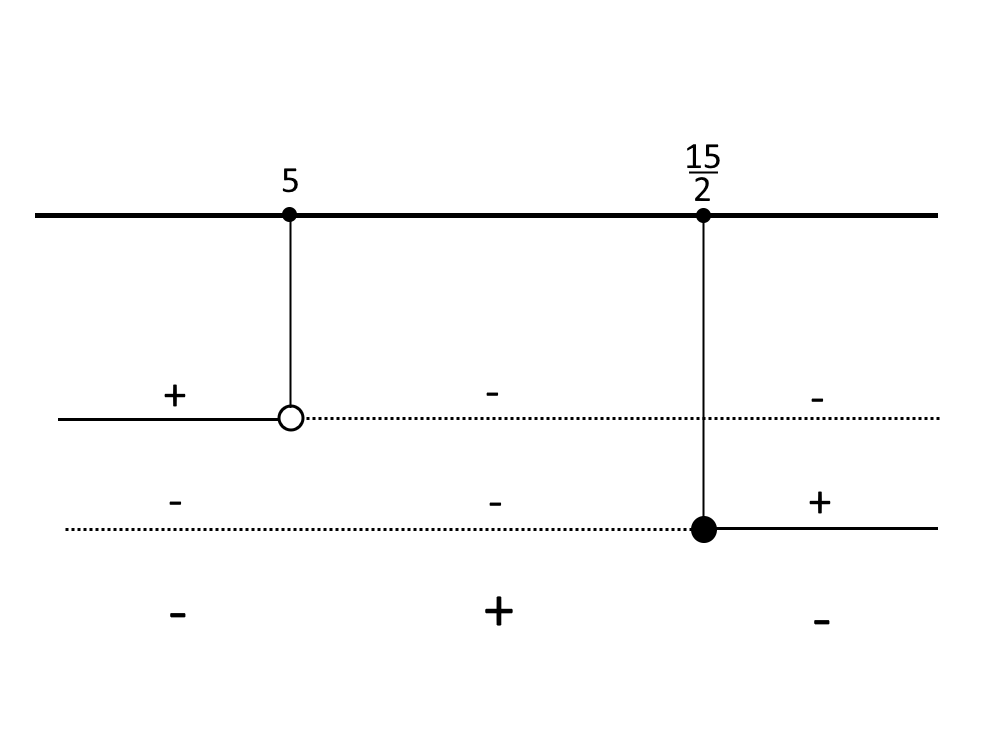
Quindi, prendendo il segno associato alla disequazione dell’esercizio, prendiamo come intervalli di soluzione quelli col segno -. Ossia:
x<5 \lor x> \frac{15}{2}
Esercizio 5. Questo è un esercizio UTILISSIMO per il proseguo, anche se non è una disequazione fratta:
x(x-1) \le 0
Abbiamo detto negli scorsi esercizi che le disequazioni fratte si risolvono con un falso sistema. Anche quando abbiamo dei prodotti, essi si risolvono con un falso sistema ancora. C’è una piccola differenza da tenere a mente!
Mentre nelle disequazioni fratte, nel falso sistema, la disequazione corrispondente al denominatore non si porta indietro il segno di uguale; nelle disequazioni con prodotti, non essendoci CE, non c’è questo problema!
Quindi il falso sistema porta con se il segno tale e quale della disequazione dell’esercizio.
\big\| x \le 0 \\ \big\| x-1 \le 0
\big\| x \le 0 \\ \big\| x \le 1
E come prima, prendiamo in considerazione gli intervalli col segno – nella tabella dei segni. Quindi la soluzione sarà:
0 \le x \le 1
Continuiamo con gli esercizi disequazioni fratte di secondo grado!
Esercizi disequazioni fratte di secondo grado
Esercizio 6. \frac{2x}{9-x^2} > 0
Il procedimento generale per la risoluzione è lo stesso, ma ci sono alcune piccole aggiunte nel corso dell’esercizio. Partiamo sempre con le condizioni di esistenza.
CE: 9-x^2 \ne 0 \implies x^2 \ne 9
e come se fosse una equazione normale:
\implies x \ne \pm \sqrt{9}
Ossia CE: x \ne \pm 3
Fatto ciò, visto che abbiamo già la forma classica del numeratore/denominatore possiamo iniziare a svolgere il falso sistema.
\big\| 2x > 0 \\ \big\| 9-x^2 > 0
\big\| x > 0 \\ \big\| -x^2 > -9
Cambiamo di segno alla seconda disequazione del falso sistema:
\big\| x > 0 \\ \big\| x^2 < 9
La seconda disequazione, se non vi ricordate come la si risolve, ve la spieghiamo. Essendo 9 un numero positivo, ed essendoci un minore(<) allora prendiamo i valori interni di:
- \sqrt{9} < x < \sqrt{9}
Ossia:
- 3 < x < 3
E mettiamo questo risultato al posto della disequazione, nel falso sistema. Otteniamo:
\big\| x > 0 \\ \big\| - 3 < x < 3
Ora procediamo con una tabella dei segni.
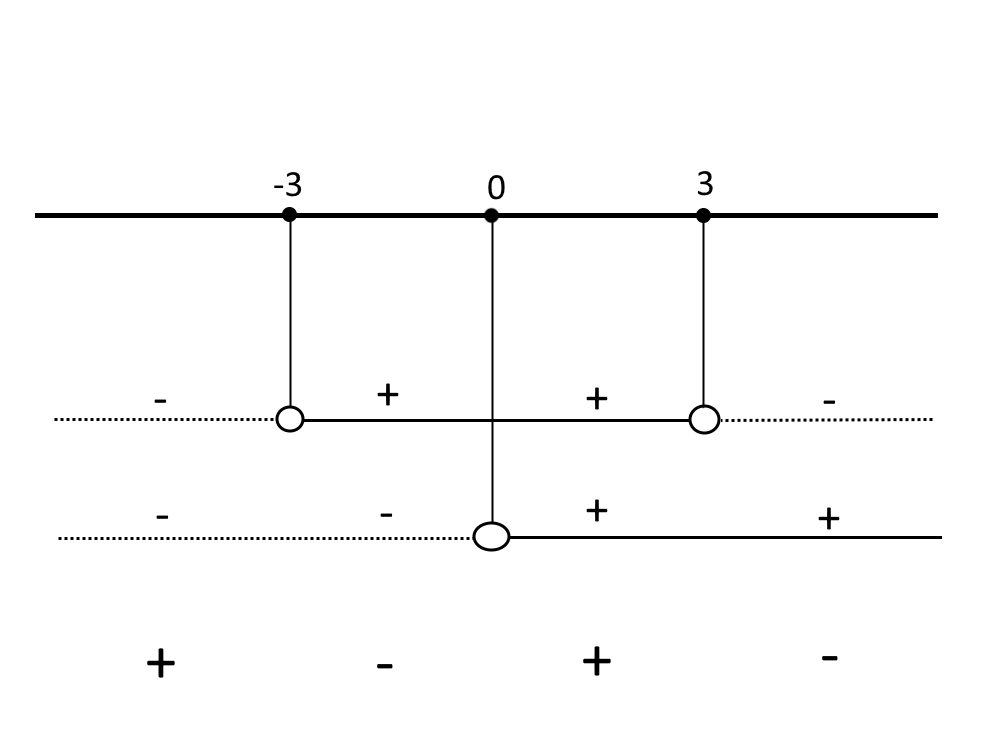
E prendiamo gli intervalli positivi (+) visto che la disequazione iniziale, è con un maggiore. La soluzione dell’esercizio è quindi:
x<-3 \lor 0<x<3
Le CE sono già incluse. Nell’esercizio 8 vedremo quando le CE non saranno incluse e dovremmo scartare delle soluzioni.
Esercizio 7. \frac{x^2 - 25}{ x + 4} \ge 0
Calcoliamo le condizioni di esistenza come sempre.
CE: x+4 \ne 0 \implies x \ne -4
Adesso passiamo direttamente al falso sistema, perchè non dobbiamo fare null’altro. Attenzione come sempre al fatto che, nella disequazione relativa al denominatore l’uguale non va messo a causa delle condizioni d’esistenza.
\big\| x^2 - 25 \ge 0 \\ \big\| x+4 > 0
\big\| x^2 \ge 25 \\ \big\| x > -4
La prima disequazione del falso sistema la si risolve come nell’esercizio precedente. Questa volta però essendoci un maggiore prendiamo i valori esterni, quindi:
x \le - 5 \lor x \ge 5
Sostituiamo questa soluzione nel falso sistema:
\big\| x \le - 5 \lor x \ge 5 \\ \big\| x > -4
Ed a questo punto andiamo a prendere nella tabella dei segni gli intervalli con il segno positivo +, visto che la disequazione è con un segno di maggiore (o uguale). La soluzione sarà:
-5 \le x < -4 \lor x \ge 5
Continuiamo con altri esercizi disequazioni fratte di secondo grado!
Esercizio 8. \frac{-x^2 -x +6 }{(x - \sqrt{2})^2} > 0
Partiamo dalle CE che in questo esercizio saranno fondamentali e finalmente vedremo perchè sono utili!
CE: (x - \sqrt{2})^2 \ne 0 \implies x - \sqrt{2} \ne 0
\implies x \ne \sqrt{2}
Ora passiamo alla scrittura del falso sistema.
\big\| -x^2 -x +6 >0 \\ \big\| (x - \sqrt{2})^2 > 0
Partiamo dalla seconda disequazione che è anche quella più veloce. Notiamo che esso è un quadrato e quindi è sicuramente positivo, per cui essa \forall x sarà >0 e quindi soddisferà la disequazione.
Sostituiamo nel falso sistema questo risultato.
\big\| -x^2 -x +6 >0 \\ \big\| \forall x
Ora prendiamo la prima disequazione e risolviamola da parte.
-x^2 -x +6 >0
Essa è una disequazione di secondo grado, quindi se non sapete come si fanno vi consiglio un attimo di esercitarvi in tale pagina cliccandoci sopra. Se sapete come si risolvono, allora come sapete partiamo col cambiare tutto di segno visto che vogliamo il termine quadratico x^2 positivo.
x^2 +x -6 < 0
Ricordatevi che quando si cambia tutto di segno una disequazione, si cambia anche il segno della disequazione stessa. Quindi qui diventa da maggiore a minore.
Ora si passa al calcolo del discriminante.
\Delta = b^2 - 4ac = 1 +24 = 25
Il discriminante è >0 e quindi andiamo a calcolare le due soluzioni distinte, come se fosse una equazione di secondo grado normale, e poi alla fine ne prendiamo i valori interni.
x_{1,2} = \frac{-b \pm \sqrt{\Delta} }{2a} = \frac{-1 \pm 5 }{2}
E quindi abbiamo:
x_1 = \frac{-1 + 5 }{2} = \frac{4 }{2} = 2
x_2 = \frac{-1 - 5 }{2} = \frac{-6}{2} = -3
Visto che la disequazione che stiamo considerando ha un segno di minore(<) andiamo a prendere i valori interni di questi due:
-3 < x < 2
Sostituiamo finalmente questo valore nel falso sistema!
\big\| -3 < x < 2 \\ \big\| \forall x
E passiamo alla tabella dei segni. Ricordatevi che \forall x si disegna con una linea piena, mentre per nessuna x con una linea tratteggiata.
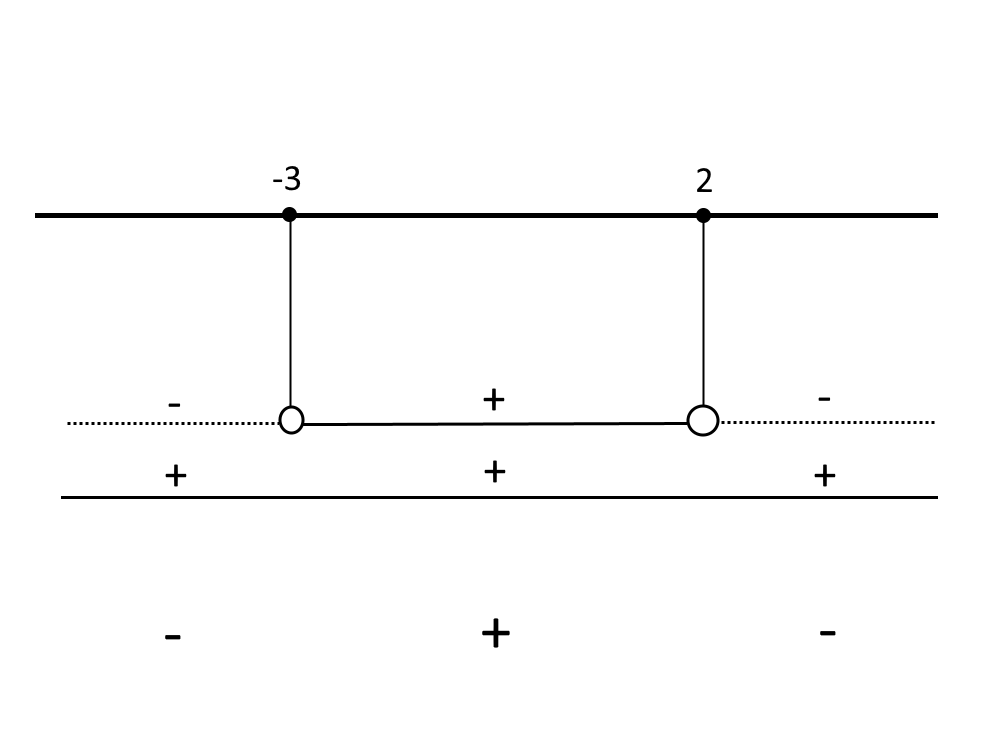
Prendiamo l’intervallo col +, e quindi:
-3 < x < 2
A questo punto intervengono le CE, perchè dentro a questo intervallo c’è un valore che non dobbiamo prendere! Le condizioni di esistenza ci dicono che la soluzione singola x=\sqrt{2} non deve essere presa! Di conseguenza correggiamo la soluzione e scriviamo:
-3 < x < 2 \land x \ne \sqrt{2}
Esercizio 9. \frac{13 + x^2 -x }{(x-5)^2} \ge 0
Prima cosa: condizioni di esistenza.
CE: (x-5)^2 \ne 0 \implies x-5 \ne 0
\implies x \ne 5
Fatto ciò passiamo immediatamente alla stesura del falso sistema:
\big\| 13 + x^2 -x \ge 0 \\ \big\| (x-5)^2 > 0
La seconda disequazione segue lo stesso discorso dell’esercizio precedente, cioè essendo un quadrato è sicuramente positivo. E quindi per ogni x.
\big\| 13 + x^2 -x \ge 0 \\ \big\| \forall x
Prendiamo da parte la prima e risolviamola.
13 + x^2 -x \ge 0
Ordiniamola un attimo:
x^2 -x +13 \ge 0
Essa è nella forma giusta, e di conseguenza non ci resta che calcolare il discriminante:
\Delta = b^2 - 4ac = 1 - 52 = -51
Il delta è negativo (<0) e, visto che la disequazione è positiva, ricordandoci della tabella delle disequazioni di secondo grado, la soluzione è semplicemente:
\forall x
Quindi sostituendo questo risultato, il nostro falso sistema diventa:
\big\| \forall x \\ \big\| \forall x
La disequazione iniziale è con un maggiore, quindi dobbiamo prendere gli intervalli positivi, ossia tutto perchè abbiamo due linee piene. La soluzione è:
\forall x
Anche qui intervengono le CE, che ci dicono che dobbiamo escludere il valore x=5. Riscriviamo la soluzione come:
\forall x \ne 5
Esercizio 10. \frac{x^2 + 9 }{x^2 -3x +2 } \ge 0
Iniziamo come sempre dalle condizioni di esistenza, che qui non sono proprio immediate.
CE: x^2 -3x +2 \ne 0
Questa, anche con la presenza della disuguaglianza, segue le stesse regole di una equazione di secondo grado normale. Quindi andiamo a calcolare il discriminante di questo polinomio.
\Delta = b^2 -4ac = 9-8=1
Delta>0 significa due soluzioni distinte. A questo punto il nostro obiettivo è calcolare queste due soluzioni e ricondurre questo polinomio nella forma seguente:
(x-x_1)(x-x_2)
Calcoliamo le soluzioni, come se fosse una equazione (alla fine rimarrà chiaramente il segno di disuguaglianza).
x_{1,2} = \frac{-b \pm \sqrt{\Delta} }{2a} = \frac{3 \pm 1 }{2}
E quindi abbiamo:
x_1 = \frac{3 + 1 }{2} = 2
x_2 = \frac{3 - 1 }{2} = 1
Ora è possibile riscrivere il polinomio iniziale come:
CE: (x-2)(x-1) \ne 0 \implies x \ne 1,2
Ora passiamo al falso sistema finalmente.
\big\| x^2 + 9 \ge 0 \\ \big\| x^2 -3x +2 > 0
\big\| x^2 \ge -9 \\ \big\| x^2 -3x +2 > 0
Partiamo dalla prima disequazione. Abbiamo un quadrato che è sempre positivo o al massimo uguale a zero, ma è sicuramente più grande di -9 sempre. Quindi la prima ha come soluzione \forall x
Passiamo alla seconda disequazione. Abbiamo già il Delta che abbiamo calcolato all’inizio, ed abbiamo le singole soluzioni già. Essendo la disequazione di secondo grado con un segno di maggiore (>), allora esse ha come soluzione i valori esterni di queste singole soluzioni, ossia:
x<1 \lor x >2
Sostituiamo il tutto nel falso sistema.
\big\| \forall x \\ \big\| x<1 \lor x >2
E di conseguenza, facendo la tabella dei segni, ci accorgiamo immediatamente che la soluzione è:
x<1 \lor x >2
Esercizio 11. \frac{ 3x^2 +5x -2 }{ x^2 +3x } \le 0
Prima di passare alle condizioni di esistenza qui risulta molto comodo mettere in evidenza una x.
\frac{ 3x^2 +5x -2 }{ x (x +3) } \le 0
A questo punto possiamo passare alle:
CE: x(x+3) \ne 0 \implies x \ne 0 \land x \ne -3
Scriviamo il falso sistema adesso:
\big\| 3x^2 +5x -2 \le 0 \\ \big\| x (x +3) < 0
Partiamo dalla prima disequazione di secondo grado, calcoliamo il discriminante.
\Delta = b^2 -4ac = 25 + 24 = 49
Delta>0 e quindi andiamoci a calcolare le soluzioni singole:
x_{1,2} = \frac{-b \pm \sqrt{\Delta} }{2a} = \frac{-5 \pm 7 }{6}
E quindi abbiamo:
x_1 = \frac{-5 + 7 }{6} = \frac{1}{3}
x_2 = \frac{-5 - 7 }{6} = -2
Visto che abbiamo la disequazione col minore, andiamo a prendere i valori interni.
-2 \le x \le \frac{1}{3}
E quindi abbiamo ora che:
\big\| -2 \le x \le \frac{1}{3} \\ \big\| x (x +3) < 0
Passiamo adesso alla risoluzione della seconda disequazione del falso sistema.
x (x +3) < 0
Questa, come visto nell’esercizio 5, è un prodotto, e lo si risolve lo stesso con un altro falso sistema ancora diverso, scritto da parte.
\big\| x < 0 \\ \big\| x +3 < 0
\big\| x < 0 \\ \big\| x < -3
Dove andiamo a prendere nel quadro dei segni l’intervallo col segno -, quindi:
-3 < x < 0
Sostituiamo il tutto nel falso sistema dell’esercizio.
\big\| -2 \le x \le \frac{1}{3} \\ \big\| -3 < x < 0
Prendiamo gli intervalli negativi, e quindi:
-3 < x \le -2 \lor 0 < x \le \frac{1}{3}
Continuiamo con gli esercizi disequazioni fratte di grado superiore al secondo!
Disequazioni fratte di grado superiore al secondo
Esercizio 12. \frac{ x^2 - 2x }{ x^3 - 6 x^2 } > 0
Come fatto nell’esercizio precedente, mettiamo in evidenza al numeratore ed al denominatore e ci semplifichiamo la vita nel campo di esistenza.
\frac{ x (x - 2) }{ x^2 (x - 6) } > 0
Ora possiamo procedere al campo di esistenza E NON A SEMPLIFICARE la x del NUMERATORE E DENOMINATORE!
CE: x^2 (x - 6) \ne 0
\implies x \ne 0 \land x \ne 6
SOLAMENTE ORA possiamo semplificare. Ricordate che prima di toccare mano all’esercizio, bisogna fare le CE, altrimenti se voi semplificate o fate qualcos’altro falsificate la scrittura delle CE.
\frac{ x - 2 }{ x (x - 6) } > 0
Ora possiamo fare il falso sistema:
\big\| x-2 > 0 \\ \big\| x (x - 6) >0
\big\| x > 2 \\ \big\| x (x - 6) >0
Risolviamo da parte, come fatto nell’esercizio precedente, la seconda disequazione. Essa è un prodotto e di conseguenza risolvibile con un altro diverso falso sistema:
\big\| x > 0 \\ \big\| x - 6 >0
\big\| x > 0 \\ \big\| x >6
Prendiamo nel quadro dei segni la parte positiva, e quindi:
x < 0 \lor x > 6
E la sostituiamo al primo falso sistema dell’esercizio iniziale:
\big\| x > 2 \\ \big\| x < 0 \lor x > 6
Facciamo un altro quadro dei segni, e prendiamo la parte positiva ancora. La soluzione è:
0<x<2 \lor x>6
Esercizio 13. \frac{x- x^3 }{4x^2 -9 } > 0
Iniziamo dalle condizioni di esistenza come sempre, prima di toccare mano alla traccia.
CE: 4x^2 -9 \ne 0 \implies x \ne \pm \frac{3}{2}
Ora passiamo alla traccia, vediamo di semplificarla: mettiamo in evidenza al numeratore la x. Si potrebbero fare altre cose, ma non conviene più di tanto, perchè non ci sarebbero comunque semplificazioni fra numeratore e denominatore. Quindi:
\frac{x ( 1- x^2 ) }{4x^2 -9 } > 0
Scriviamo il falso sistema.
\big\| x ( 1- x^2 ) > 0 \\ \big\| 4x^2 -9 > 0
\big\| x ( 1- x^2 ) > 0 \\ \big\| x^2 > \frac{9}{4}
Partiamo dalla prima disequazione del falso sistema, che si risolve a parte con un altro falso sistema, essendo un prodotto. Scriviamo il falso sistema di questo termine:
\big\| x > 0 \\ \big\| 1- x^2 > 0
\big\| x > 0 \\ \big\| - x^2 > -1
Cambiamo di segno al secondo termine:
\big\| x > 0 \\ \big\| x^2 < 1
Il secondo termine, come detto tante volte, ha come soluzione i valori interni fra -1 ed 1, ossia le sue radici con segno diverso. Sostituiamo tale risultato nel falso sistema:
\big\| x > 0 \\ \big\| -1 < x < 1
Ed ora grazie al quadro dei segni, prendiamo la parte col segno positivo, che è:
x < -1 \lor 0 < x < 1
Sostituiamo finalmente nel falso sistema dell’esercizio tale risultato:
\big\| x < -1 \lor 0 < x < 1 \\ \big\| x^2 > \frac{9}{4}
Ci manca il secondo termine: esso avendo un maggiore, prendiamo i valori esterni delle sue radici.
\big\| x < -1 \lor 0 < x < 1 \\ \big\| x<- \frac{3}{2} \lor x > \frac{3}{2}
Adesso possiamo fare il quadro dei segni del falso sistema della disequazione dell’esercizio, e prendiamo la parte positiva. Ricordatevi che ogni rigo del falso sistema si scrive su una unica linea, e non su linee diverse, anche se ci sono più intervalli. La soluzione è:
x<- \frac{3}{2} \lor -1 < x 0 \lor 1 < x < \frac{3}{2}
Esercizio 15. \frac{ 16 - x^4 }{27 - x^3} > 0
Possiamo passare alle CE, ma se non sapete come trattare un grado superiore al secondo, allora procediamo con una scomposizione. Potete mettere in evidenza quello che volete, l’importante è che non semplificate prima di fare le CE!
Utilizziamo la formula della differenza di cubi:
A^3 - B^3 = (A-B)(A^2 + AB + B^2)
Dove nel nostro caso, al denominatore
A=3, \; B=x
Quindi possiamo utilizzare la formula riscrivendo il denominatore come:
\frac{ 16 - x^4 }{ (3-x)(x^2 + 3x + 9) } > 0
A questo punto possiamo fare le condizioni di esistenza perchè ne siamo in grado.
CE:3-x \ne 0 \implies x \ne 3
E poi abbiamo l’altro termine al denominatore:
CE: x^2 + 3x + 9 \ne 0
Andiamoci a calcolare il discriminante per la risoluzione, trattandolo come una semplice equazione di secondo grado.
\Delta = b^2 - 4ac = 9-36 = -25 <0
Delta<0, e quindi significa che non ha soluzione, quindi questo non ci dà nessuna ulteriore CE.
Ora possiamo andare avanti! Ritorniamo all’esercizio:
\frac{ 16 - x^4 }{ (3-x)(x^2 + 3x + 9) } > 0
Prima di fare il falso sistema, visto che non siamo in grado di fare le disequazioni di quarto grado, scomponiamo il numeratore usando la formula della differenza di quadrati:
a^2 - b^2 = (a-b)(a+b)
Dove nel nostro caso abbiamo:
4^2 - (x^2)^2 = (4-x^2)(4+x^2)
\frac{ (4-x^2)(4+x^2) }{ (3-x)(x^2 + 3x + 9) } > 0
Ora possiamo scrivere il falso sistema:
\big\| (4-x^2)(4+x^2) > 0 \\ \big\| (3-x)(x^2 + 3x + 9) > 0
Non spaventiamoci, facciamo le cose con calma ed un passo alla volta. Iniziamo dal primo termine: esso è un prodotto e lo si risolve con un altro falso sistema.
\big\| 4-x^2 > 0 \\ \big\| 4+x^2 > 0
\big\| -x^2 > -4 \\ \big\| x^2 > -4
Cambiamo di segno al primo termine:
\big\| x^2 < 4 \\ \big\| x^2 > -4
Il secondo termine ha come soluzione per ogni x, perché abbiamo che un quadrato è sempre positivo e quindi sicuramente più grande di -4. Il primo termine ha un minore e quindi prendiamo i valori interni delle sue radici:
\big\| -2 < x < 2 \\ \big\| \forall x
Prendiamo i valori positivi nel quadro dei segni, che ci portano a:
-2 < x < 2
Sostituiamo nel falso sistema iniziale.
\big\| -2 < x < 2 \\ \big\| (3-x)(x^2 + 3x + 9) > 0
Passiamo al secondo termine. Abbiamo un prodotto e quindi facciamo un altro falso sistema ancora.
\big\| 3-x > 0 \\ \big\| x^2 + 3x + 9 > 0
\big\| x < 3 \\ \big\| x^2 + 3x + 9 > 0
Il secondo termine è una disequazione di secondo grado, dove noi già abbiamo calcolato il discriminante.
Ricordiamo che: Delta<0 con una disequazione con segno >, allora si ha che la soluzione è:
\forall x
Quindi:
\big\| x < 3 \\ \big\| \forall x
Nel quadro dei segni prendiamo la parte positiva che è:
x<3
Sostituiamo nel falso sistema iniziale e concludiamo l’esercizio!
\big\| -2 < x < 2 \\ \big\| x<3
Abbiamo come soluzione:
-2 < x < 2 \lor x > 3
Abbiamo visto come svolgere esercizi disequazioni fratte, di primo grado, del secondo o anche superiori. Potete trovare altri argomenti e centinaia di altri esercizi svolti sulle pagine di matematica che altro ancora!
Per approfondire:
https://it.wikipedia.org/wiki/Disequazione_fratta
grafico
disequazioni