Equazioni goniometriche elementari: 20 ESERCIZI
Equazioni goniometriche elementari: 20 ESERCIZI! Basterà una giornata su questa pagina per capire come si fanno le equazioni goniometriche elementari: sarete pronti per la verifica! Prima di applicarvi su queste, vi consiglio saper fare prima le identità goniometriche. Partiamo con un indice che suddivide gli argomenti di questa pagina.
Indice
- Equazioni elementari con il seno
- Equazioni elementari con il coseno
- Equazioni elementari con la tangente
- Equazioni riconducibili ad elementari
Iniziamo subito con le equazioni goniometriche elementari con esercizi svolti!
Equazioni goniometriche elementari
esercizi con il seno
Esercizio 1. 2 \sin x = \sqrt{3}
Iniziamo come nelle classiche equazioni che avete sempre fatto, ad isolare l’incognita. In questo caso andiamo a dividere tutto per 2 per isolare il seno:
\sin x = \frac{\sqrt{3}}{2}
Ora che il seno è isolato, prendiamo in considerazione la circonferenza goniometrica. Visto che il seno rappresenta la componente dell’angolo sull’asse delle y, tracciamo una retta orizzontale che parte dal punto y=\frac{\sqrt{3}}{2} , come in figura.
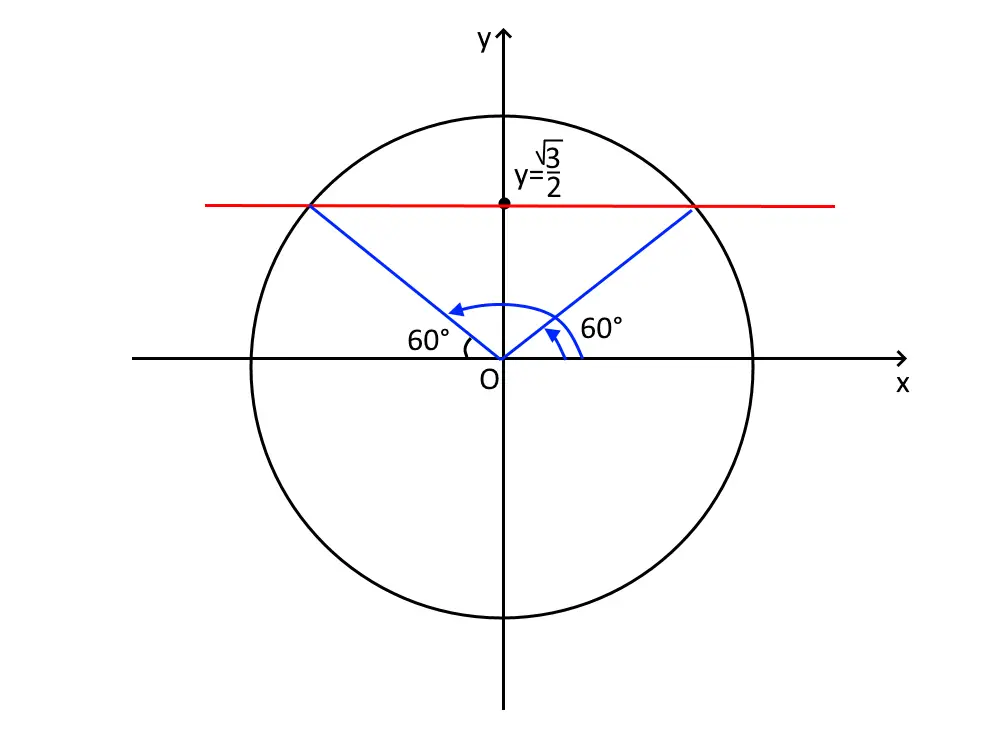
Nell’immagine potete notare due angoli: il primo ce lo darà la calcolatrice, il secondo lo ricaviamo noi. Prendiamo quindi la calcolatrice: premiamo shift e poi seno, ed inseriamo il valore di \frac{\sqrt{3}}{2} . Ci uscirà fuori:
x=60°=\frac{\pi}{3}
A questo punto dobbiamo ricavare l’altro angolo. Come potete vedere dalla figura, si capisce bene che l’altro angolo è 180° – l’angolo calcolato nel primo quadrante:
\pi - \frac{\pi}{3} =\frac{3\pi -\pi}{3} = \frac{2}{3} \pi
Ora, abbiamo le due soluzioni. Ci dobbiamo a questo punto, aggiungere la periodicità della funzione seno per entrambe le soluzioni:
x=\frac{\pi}{3} +2k\pi \lor x= \frac{2}{3} \pi +2k\pi
Quindi, se avete il seno, dovete tracciare una retta che passa sull’asse delle y!
Esercizio 2. \sin x -1= 0
Isoliamo il seno, portando il -1 dall’altra parte, viene:
\sin x = 1
A questo punto. è l’ora di tracciare la circonferenza goniometrica per capire gli angoli soluzione. Come possiamo vedere l’unico punto in cui il seno è 1 è quando l’angolo è:
x=90°= \frac{\pi}{2}
Non c’è nessun altro angolo da ricavare in questo caso, quindi aggiungiamo semplicemente la periodicità per ottenere la soluzione completa dell’esercizio:
x= \frac{\pi}{2} + 2k \pi
Esercizio 3. 2 \sin x -4 = 3
Iniziamo a portare il -4 dall’altra parte:
2 \sin x = 3 +4
2 \sin x = 7
Dividiamo tutto per 2 per isolare il seno:
\sin x = \frac{7}{2}
Otteniamo che il seno è uguale a \frac{7}{2} =3,5
Ma visto che la funzione seno ha sempre valori fra -1 ed 1, è impossibile per qualsiasi angolo che essa sia 3,5. Quindi la soluzione è:
impossibile
Esercizio 4. 2 \sin x = - \sqrt{2}
Dividiamo tutto per 2, ottenendo:
\sin x = - \frac{\sqrt{2}}{2}
Prendiamo la circonferenza goniometrica, come prima, e tracciamo una retta orizzontale passante per il punto y = - \frac{\sqrt{2}}{2}
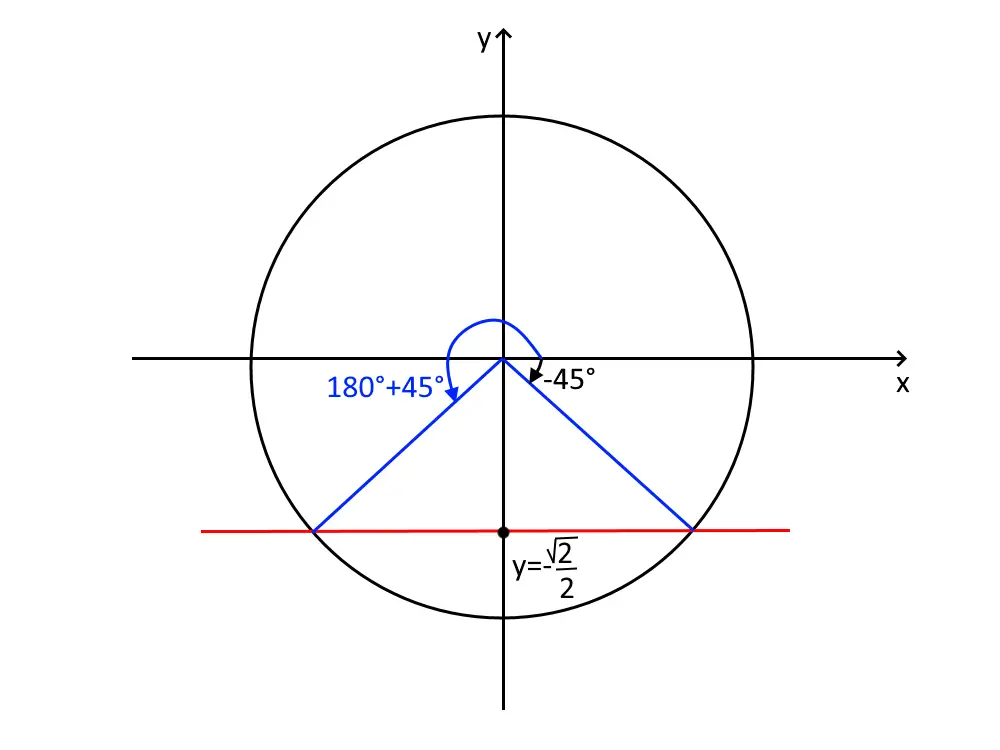
Abbiamo visibilmente due angoli come soluzione. Prendiamo la calcolatrice, premiamo shift e poi seno ed inseriamo il valore. Uscirà fuori questa volta un angolo negativo:
x=-45°
Ossia la calcolatrice ci dà l’angolo nel quarto quadrante. Per passare allo stesso angolo ma scritto positivo, basterà aggiungere un angolo giro:
x=-45° +360° = 315°
Per passare ai radianti, utilizziamo la proporzione utilissima che vi consiglio di segnarvi seguente:
360° : 2\pi = 315° : x
x = \frac{2\pi \cdotp 315°}{360°}
Dividiamo per 45 (voi potete dividere mano mano per quello che volete, è uguale):
x = \frac{2\pi \cdotp 7}{8}= \frac{ 7}{4} \pi
A questo punto abbiamo ricavato il primo angolo! Per l’altro angolo, notiamo dalla figura che esso è uguale a:
x=180°+45°= \pi + \frac{\pi}{4} = \frac{5}{4} \pi
E’ IMPORTANTISSIMO VEDERE LA FIGURA E GLI ANGOLI CHE CI SONO PER ARRIVARE ALLA SOLUZIONE!
A questo punto aggiungiamo la periodicità del seno, ed abbiamo concluso l’esercizio.
x= \frac{5}{4} \pi + 2k\pi \lor x=\frac{ 7}{4} \pi + 2k\pi
Continuiamo con le equazioni goniometriche elementari con altri esercizi svolti!
Esercizio 5. 2 \sin \frac{x}{2} = 1
Iniziamo ad isolare il seno, dividendo tutto per 2:
\sin \frac{x}{2} = \frac{1}{2}
A questo punto, si procede per sostituzione.
Poniamo t=\frac{x}{2}
\sin t = \frac{1}{2}
E siamo arrivati ad una forma di equazione che conosciamo già!
Prendiamo la circonferenza goniometrica e tracciamo la retta. Prendiamo la calcolatrice ed otteniamo l’angolo nel primo quadrante:
t=30°= \frac{\pi}{6}
Attenzione che qui abbiamo t non x! L’altro lo calcoliamo guardando la figura, e notando che esso è semplicemente:
t=180° - 30° = \pi - \frac{\pi}{6} = \frac{6\pi -\pi}{6} = \frac{5}{6} \pi
A questo punto, come fatto per gli altri esercizi aggiungiamo la periodicità del seno ed otteniamo le due soluzioni in t.
t= \frac{\pi}{6} + 2k\pi \lor t= \frac{5}{6} \pi + 2k\pi
Ora però l’esercizio non è finito, dobbiamo ripassare alla variabile iniziale x. Quindi ritorniamo risostituendo il valore:
t=\frac{x}{2}
Sostituiamo nella soluzione.
\frac{x}{2}= \frac{\pi}{6} + 2k\pi \lor \frac{x}{2}= \frac{5}{6} \pi + 2k\pi
Moltiplichiamo tutto per 2, così da avere solo la x da sola.
2\frac{x}{2}= 2\frac{\pi}{6} + 4k\pi \lor 2\frac{x}{2}= 2\frac{5}{6} \pi + 4k\pi
x= \frac{\pi}{3} + 4k\pi \lor x= \frac{5}{3} \pi + 4k\pi
Ed abbiamo concluso l’esercizio!
Esercizio 6. \sin (\frac{\pi}{3} - x) = 0
Come prima, o comunque in generale: quando non avete una x semplice, procedete per sostituzione. Di fatti poniamo:
t= \frac{\pi}{3} - x
\sin t = 0
Disegniamo la circonferenza goniometrica, e ci accorgiamo che il seno è uguale a zero negli angoli 0 e \pi . Questi si alternano di 180° in 180°, e quindi si possono anche scrivere in maniera compatta come:
t=k\pi
A questo punto ritorniamo alla variabile iniziale!
\frac{\pi}{3} - x =k\pi
Isoliamo la x ed otteniamo la soluzione all’esercizio:
x =\frac{\pi}{3} - k\pi
Nella periodicità il segno è indifferente: è per questo che il libro porta come risultato:
x =\frac{\pi}{3} + k\pi
Esercizio 7. 4 \sin x = -1
Questo è un caso un poco diverso dagli altri, ora vedremo perchè. Iniziamo a dividere tutto per 4:
\sin x = - \frac{1}{4}
Ora se provate a trovare l’angolo corrispondente con la calcolatrice, uscirà fuori un angolo negativo strano e non preciso, quindi sarà impossibile passare ai radianti. Quando l’angolo risultante non è ben definito, lo lasciamo in arcseno, nel modo seguente:
x = \arcsin (- \frac{1}{4})
Questo rappresenta l’angolo nel quarto quadrante, visto che l’arcseno è definito nell’intervallo [-\frac{\pi}{2},\frac{\pi}{2}].
Per trovare l’altra soluzione, tracciamo come sempre la circonferenza goniometrica, e notiamo come visto più volte che l’altro angolo soluzione è:
x=\pi - \arcsin (- \frac{1}{4})
Perchè abbiamo sottratto e non aggiunto? Perchè dovete considerare che l’angolo \arcsin (- \frac{1}{4}) è un angolo negativo, come ci ha detto la calcolatrice. Ecco perchè abbiamo messo il segno -. Dopo ciò aggiungiamo la periodicità del seno.
x = \arcsin (- \frac{1}{4}) +2k\pi \lor x= \pi - \arcsin (- \frac{1}{4}) +2k\pi
Continuiamo con le equazioni goniometriche elementari con altri esercizi svolti!
Equazioni goniometriche elementari
esercizi con il coseno
Esercizio 9. \cos x = \frac{\sqrt{2}}{2}
Per trovare le soluzioni (angoli) del coseno, andiamo come fatto anche per il seno, a disegnare la circonferenza goniometrica. Però, a differenza del seno, la retta qui deve essere verticale e passante per X=\frac{\sqrt{2}}{2} , come in figura.
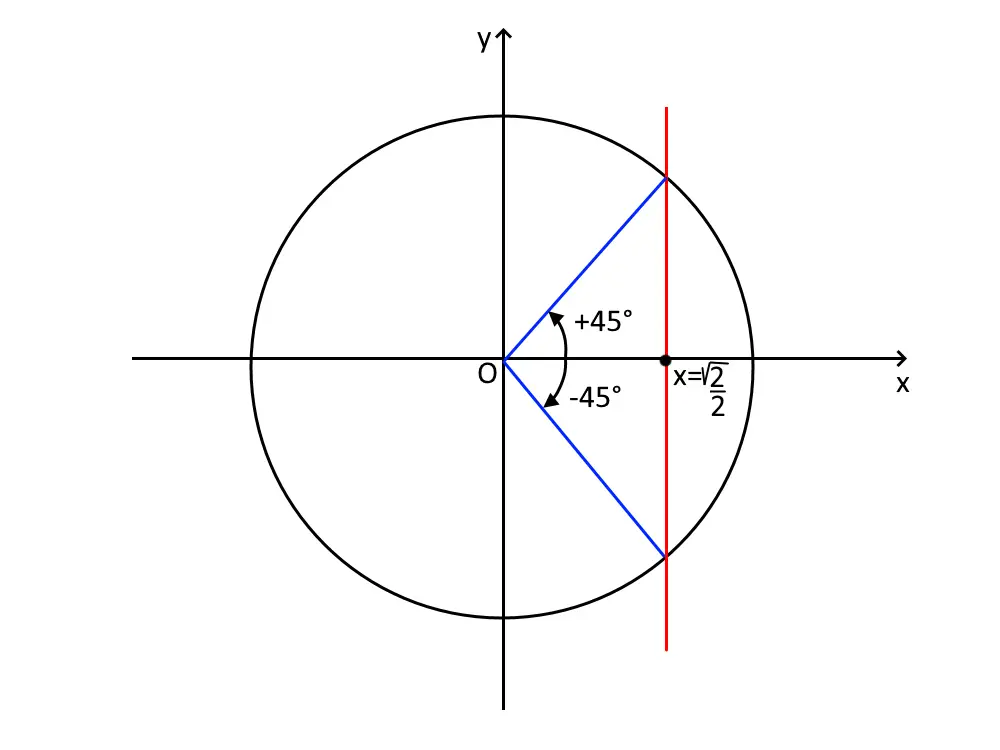
Notiamo subito che gli angoli del coseno si possono trovare molto facilmente! Questo perchè se calcoliamo l’angolo del primo quadrante con la calcolatrice, essa ci dice che l’angolo è:
x=45°=\frac{\pi}{4}
Vista la simmetria del coseno intorno allo zero, l’altro angolo è lo stesso ma con un segno negativo! E’ molto più semplice!
Di fatti l’altro è:
x=-\frac{\pi}{4}
Aggiungiamo la periodicità del coseno, ed otteniamo in maniera molto compatta la soluzione:
x= \pm \frac{\pi}{4} + 2k\pi
Esercizio 10. 8 \cos x = 1
Dividiamo tutto per 8, ottenendo:
\cos x = \frac{1}{8}
Disegniamo la circonferenza goniometrica e la retta passante per il punto X= \frac{1}{8} . La calcolatrice ci dice un angolo strano, quindi lo rimaniamo così, scrivendolo come un arccoseno.
x =\arccos ( \frac{1}{8} )
L’altro angolo è semplicemente lo stesso, ma con un segno negativo, come detto prima.
x =- \arccos ( \frac{1}{8} )
Aggiungiamo la periodicità e scriviamo in maniera compatta la soluzione:
x =\pm \arccos ( \frac{1}{8} ) +2k\pi
Esercizio 11. \cos (\frac{\pi}{9} - x ) = 0
Questo è un caso molto simile al seno, procediamo per sostituzione. Poniamo:
t=\frac{\pi}{9} - x
\cos t = 0
Vediamo che nella circonferenza goniometrica, il coseno è pari a 0 negli angoli \frac{\pi}{2} e \frac{\pi}{2} , questo lo possiamo scrivere in maniera compatta come:
t=\frac{\pi}{2} + k\pi
Ritorniamo alla variabile x iniziale adesso, risostituendo.
\frac{\pi}{9} - x =\frac{\pi}{2} + k\pi
Isoliamo la x.
- x =- \frac{\pi}{9} + \frac{\pi}{2} + k\pi
Cambiamo di segno tutto.
x = \frac{\pi}{9} - \frac{\pi}{2} + k\pi
(la periodicità rimane dello stesso segno, è uguale)
x = \frac{11}{18}\pi + k\pi
Esercizio 12. 5 \cos (x-\frac{\pi}{9} ) +3 = 3\cos (x-\frac{\pi}{9} ) +4
Procediamo anche in questo caso ponendo:
t= x-\frac{\pi}{9}
5 \cos t +3 = 3\cos t +4
5 \cos t - 3\cos t = 1
I coseni sono uguali, quindi li posso sommare!
2 \cos t = 1
\cos t = \frac{1}{2}
Disegniamo la circonferenza goniometrica e la retta passante per il punto X = \frac{1}{2}
Il primo angolo ce lo dà la calcolatrice ed è:
t= 60°= \frac{\pi}{3}
Ed il secondo angolo è semplicemente lo stesso ma negativo.
t=-\frac{\pi}{3}
Qui scriviamo la soluzione non in maniera compatta, perchè dovremmo ancora fare altri calcoli!
t= \frac{\pi}{3} +2k\pi \lor t=- \frac{\pi}{3} +2k\pi
Ritorniamo alla variabile iniziale adesso.
x-\frac{\pi}{9} = \frac{\pi}{3} +2k\pi \lor x-\frac{\pi}{9} =- \frac{\pi}{3} +2k\pi
x = \frac{\pi}{3} +\frac{\pi}{9}+2k\pi \lor x =- \frac{\pi}{3}+\frac{\pi}{9} +2k\pi
x = \frac{4\pi}{9} +2k\pi \lor x =- \frac{2\pi}{9}+2k\pi
Continuiamo con le equazioni goniometriche elementari con altri esercizi svolti!
Equazioni goniometriche elementari
esercizi con la tangente
Esercizio 13. \tg x = 1
Il discorso è analogo con le altre due funzioni goniometriche; certamente ci sono alcune differenze che ora vedremo! Disegniamo la circonferenza goniometrica. Qui, andiamo a disegnare una retta tangente all’angolo zero verticale. L’angolo corrispondente sarà dato dal congiungere l’origine con il punto 1 sulla retta tangente, come in figura.
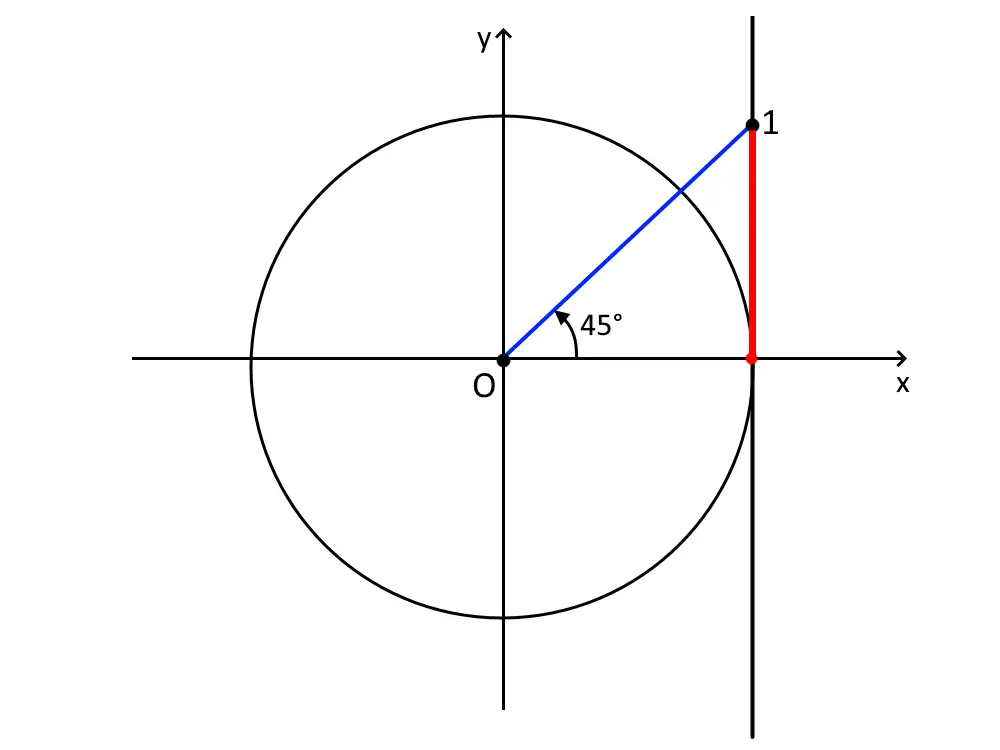
La calcolatrice ci dice che l’angolo nel primo quadrante corrispondente è:
x=45°=\frac{\pi}{4}
Per la tangente la cosa bella è che non c’è bisogno di calcolare altre soluzioni! Aggiungiamo semplicemente la periodicità della tangente ed il gioco è fatto!
x=\frac{\pi}{4} +k\pi
Esercizio 14. \tg \frac{x}{4} +1 = 0
Portiamo l’uno dall’altra parte isolando la tangente.
\tg \frac{x}{4} = -1
Essendo un angolo non con sola x, andiamo per sostituzione:
z=\frac{x}{4}
\tg z = -1
La calcolatrice ci dà come risultato un angolo negativo e a noi va benissimo, sulla tangente non ci dobbiamo porre troppi problemi.
z= -45°= - \frac{\pi}{4}
a cui aggiungiamo la periodicità della tangente:
z= - \frac{\pi}{4} +k\pi
Torniamo alla variabile x.
\frac{x}{4}= - \frac{\pi}{4} +k\pi
Moltiplichiamo tutto per 4, e l’esercizio è concluso!
x= -\pi +4k\pi
Esercizio 15. 3\cotg 3x =- \sqrt{3}
Allora non spaventiamoci per la presenza della cotangente, essa non è un problema assolutamente. Facciamo una cosa alla volta, e quindi iniziamo a dividere per 3.
\cotg 3x =- \frac{ \sqrt{3}}{3}
Poi poniamo z=3x, come fatto già tante altre volte.
\cotg z =- \frac{ \sqrt{3}}{3}
A questo punto ricordiamo la relazione fra tangente e cotangente e sfruttiamola, portando l’equazione in termini della tangente.
\cotg \alpha = \frac{1}{\tg \alpha }
E quindi la nostra equazione diventa:
\frac{1}{\tg z } =- \frac{ \sqrt{3}}{3}
Ora, facciamo il reciproco di tutto, invertendo denominatori e numeratori:
\tg z =- \frac{3 }{\sqrt{3}}
A questo punto siamo arrivati ad una equazione goniometrica elementare con sola tangente! Che sappiamo risolvere! Infatti, disegniamo la circonferenza goniometrica, ed utilizzando la calcolatrice abbiamo che:
z=- \frac{\pi}{3} +k\pi
E torniamo alla variabile iniziale ed il gioco è fatto!
3x=- \frac{\pi}{3} +k\pi
x=- \frac{\pi}{9} +k \frac{\pi}{3}
Esercizio 16. \cotg 2x = 1
Questo è come prima! Provate a farlo voi e poi vedete la soluzione, dai!
Poniamo innanzitutto 2x=z:
\cotg z = 1
Poi sfruttiamo la relazione fra tangente e cotangente citata nell’esercizio precedente, per arrivare ad una equazione si sola tangente che sappiamo risolvere.
\frac{1}{\tg z } = 1
Facciamo il reciproco di tutto; il reciproco di 1 è sempre 1!
\tg z = 1
Vedendo l’angolo alla calcolatrice abbiamo la soluzione:
z= \frac{\pi}{4} + k\pi
2x= \frac{\pi}{4} + k\pi
x= \frac{\pi}{8} + k\frac{\pi}{2}
Continuiamo con le equazioni goniometriche elementari con altri esercizi svolti!
Equazioni goniometriche riconducibili a elementari
Esercizio 17. 2 \cos^2 x - \cos x = 0
Quello che dobbiamo fare è ricondurre queste equazioni a quelle che abbiamo appena visto e che sappiamo risolvere. In questo caso quello che possiamo fare è mettere in evidenza il coseno:
\cos x (2 \cos x - 1 ) = 0
E questa equazione è uguale a zero, se:
\cos x = 0 \lor 2 \cos x - 1 = 0
Svolgiamole separatamente. Iniziamo dalla prima: il coseno è uguale a zero per angoli di 90° o 270° che possiamo scrivere in maniera compatta come:
x = \frac{\pi}{2} + k\pi
Mentre la seconda equazione è:
2 \cos x - 1 = 0
\cos x = \frac{1}{2}
Questa è una equazione goniometrica elementare del coseno, che sappiamo risolvere. Disegniamo la circonferenza goniometrica e ci accorgiamo che i due angoli soluzione sono uguali ma di segno opposto. La calcolatrice ci dà l’angolo del primo quadrante:
x=\frac{\pi}{3}
L’altro è x=-\frac{\pi}{3}
A cui ci aggiungiamo la periodicità e scriviamo come:
x= \pm \frac{\pi}{3} +2k\pi
Ora, uniamo anche l’altra soluzione ed otteniamo:
x = \frac{\pi}{2} + k\pi \lor x= \pm \frac{\pi}{3} +2k\pi
Esercizio 18. 2 \cos^2 x - \sin x -1 = 0
Qui abbiamo un coseno ed un seno, insieme non ci piacciono. Però ricordandoci della prima relazione fondamentale della goniometria, possiamo passare dal coseno a scrivere tutto in funzione del seno.
\sin^2 x + \cos^2 x = 1
\cos^2 x = 1 - \sin^2 x
Andiamo a sostituire ed ci siamo levati da mezzo il coseno!
2 (1 - \sin^2 x) - \sin x -1 = 0
2 - 2 \sin^2 x - \sin x -1 = 0
1 - 2 \sin^2 x - \sin x = 0
Ora procediamo per sostituzione, perchè ponendo t= \sin x esce fuori una equazione di secondo grado!
1 - 2 t^2 - t = 0
2 t^2 + t -1 = 0
Calcoliamo le due soluzioni di questa equazione di secondo grado:
t_{1,2}= \frac{-1 \pm 3}{4} = \frac{1}{2} , -1
Risostituiamo e torniamo al seno! Come potete vedere la sostituzione avviene molto spesso nelle equazioni goniometriche elementari!
\sin x = \frac{1}{2} \lor \sin x = -1
Svolgiamole separatamente. Nel secondo caso che è semplice abbiamo che l’unico angolo per il quale il seno è -1 è:
x = \frac{3}{2} \pi + 2k\pi
Per la prima equazione invece, utilizziamo i metodi usati all’inizio di questa pagina.
\sin x = \frac{1}{2}
Il primo angolo ce lo dà la calcolatrice ed è:
x=\frac{\pi}{6}
L’altro, disegnando una circonferenza goniometrica ci accorgiamo che è:
x=\pi - \frac{\pi}{6} = \frac{5}{6}\pi
Uniamo tutte le soluzioni adesso! Otteniamo:
x = \frac{3}{2} \pi + 2k\pi \lor x=\frac{\pi}{6} +2k\pi \lor \frac{5}{6}\pi + 2k\pi
Esercizio 19. \sin 2x + \sin 3x + \sin 4x = 0
Questa è difficile. Ma la professoressa ve la potrebbe mettere nel compito, voi sarete preparati però! Qui bisogna sfruttare la formula di prostaferesi seguente:
\sin p + \sin q = 2 \sin \frac{p+q}{2} \cos \frac{p-q}{2}
Facciamolo per esempio (voi fate come volete) fra il terzo ed il primo termine dell’equazione ed otteniamo:
2 \sin 3x \cos x + \sin 3x = 0
Mettiamo in evidenza il seno e l’equazione ora con un solo passaggio è diventata più semplice!
\sin 3x (2 \cos x + 1) = 0
Risolviamo il primo pezzo \sin 3x = 0 .
Poniamo z=3x.
\sin z = 0
Il seno è uguale a zero negli angoli:
z= k\pi
3x= k\pi
x= k \frac{\pi}{3}
Ora possiamo passare a studiare il secondo pezzo.
2 \cos x + 1= 0
\cos x = - \frac{1}{2}
che ha come soluzioni:
x = \pm \frac{2}{3}\pi +2k\pi
Unendo le due soluzioni, notiamo che il tutto è compreso in:
x= k \frac{\pi}{3}
Esercizio 20. \cos 2x + \cos 3x + \cos 4x +\cos 5x = 0
Anche in questo caso utilizziamo la formula di prostaferesi seguente:
\cos p + \cos q = 2 \cos \frac{p+q}{2} \cos \frac{p-q}{2}
Per non portare dietro frazioni, utilizziamo questa formula fra primo e terzo termine, e fra secondo e quarto:
2 \cos 3x \cos x + 2 \cos 4x \cos x = 0
Dividiamo per 2 tutto:
\cos 3x \cos x + \cos 4x \cos x = 0
Mettiamo in evidenza il coseno:
\cos x (\cos 3x + \cos 4x ) = 0
All’interno della parentesi utilizziamo un’altra volta la stessa formula di prostaferesi.
2 \cos x \cos \frac{7x}{2} \cos \frac{x}{2} = 0
Quindi questa equazione è zero, se almeno uno dei tre risulta essere zero. Quindi li risolviamo separatamente:
\cos x = 0
Da cui segue x= \frac{\pi}{2}+k\pi
\cos \frac{7x}{2} = 0
Da cui segue \frac{7x}{2} = \frac{\pi}{2}+k\pi
E quindi x = \frac{\pi}{7}+ k \frac{2\pi}{7}
Poi rimane l’ultima equazione:
\cos \frac{x}{2} = 0
Da cui segue \frac{x}{2}= \frac{\pi}{2}+k\pi
che implica x= \pi+2k\pi
Unendo le soluzioni, notiamo che a noi basta prendere:
x=\frac{\pi}{2}+k\pi \lor x= \frac{\pi}{7}+ k \frac{2\pi}{7}
Per essere preparati per la verifica in classe vi consigliamo anche di esercitarvi sulle identità goniometriche!
Continuate a studiare sul nostro sito: trovate centinaia di altri esercizi di matematica che altro ancora!
Per approfondire: https://it.wikipedia.org/wiki/Equazione_trigonometrica
Equazioni goniometriche elementari: 20 esercizi.
goniometriche
esercizi
goniometriche
eserizi