Identità goniometriche: 15 ESERCIZI SVOLTI !
Identità goniometriche: 15 ESERCIZI SVOLTI ! Per la verifica in classe si può essere assolutamente pronti vedendo come si svolgono questi 15 esercizi svolti: in una giornata avrete imparato come farli! Introduciamo la pagina con un indice che divide i vari argomenti, fateli uno alla volta con calma. Iniziamo subito!
Indice
- Identità goniometriche con seno e coseno
- Identità goniometriche con tang e cotang
- Identità goniometriche con secante e cosecante
- Consigli generali
Iniziamo subito con le identità goniometriche esercizi svolti!
Identità seno e coseno
esercizi
In questo capitoletto vedremo come si risolvono delle identità seno e coseno esercizi.
Esercizio 1. (\sin \alpha + \cos \alpha )^2 -1 = 2 \sin \alpha \cos \alpha
Un esercizio di identità goniometrica consiste nel risolvere l’espressione di sinistra e renderla uguale a quella di destra tramite passaggi algebrici o con l’utilizzo di formule goniometriche. In questo caso andiamo a svolgere il quadrato a primo membro. Il secondo membro non lo tocchiamo! Quindi prendiamo solo il primo membro:
(\sin \alpha + \cos \alpha )^2 -1 = \sin^2 \alpha + \cos^2 \alpha + 2 \sin \alpha \cos \alpha -1 =
A questo punto utilizziamo la prima relazione fondamentale della goniometria:
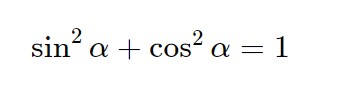
E quindi la nostra espressione diventa:
=1 + 2 \sin \alpha \cos \alpha -1 = 2 \sin \alpha \cos \alpha
E siamo arrivati ad una espressione che è la stessa del secondo membro! Abbiamo quindi verificato l’identità !
Questi esercizi consistono in questo.
Esercizio 2. \sin \alpha \cdotp \cos^2 \alpha + \sin^3 \alpha = \sin \alpha
Ancora una volta andiamo ad utilizzare la prima relazione fondamentale della goniometria. Essa lega il seno ed il coseno al quadrato, quindi quando vediamo un seno/coseno al quadrato vi deve venire in mente questa formula:
\sin^2 \alpha + \cos^2 \alpha = 1
Questo perchè portando il seno dall’altra parte, otteniamo il coseno in funzione del seno:
\cos^2 \alpha = 1 -\sin^2 \alpha
Ed andiamo a sostituire, in questo modo abbiamo tutto in funzione del seno, visto che il secondo membro dell’esercizio è un seno: non ci sono coseni! Andiamo a sostituire:
\sin \alpha \cdotp \cos^2 \alpha + \sin^3 \alpha = \sin \alpha ( 1 -\sin^2 \alpha )+ \sin^3 \alpha =
Svolgiamo la moltiplicazione.
= \sin \alpha -\sin^3 \alpha + \sin^3 \alpha = \sin \alpha
Ed abbiamo risolto l’esercizio, siamo arrivati alla stessa forma che l’esercizio voleva!
Esercizio 3. \sin^2 \alpha + \sin^2 \alpha \cdotp \cos^2 \alpha + \cos^4 \alpha = 1
Qui quello che dà fastidio sicuramente è quel \cos^2 \alpha , quindi dobbiamo cercare di abbassargli il grado, di fatto lo possiamo sicuramente scrivere come:
\sin^2 \alpha + \sin^2 \alpha \cdotp \cos^2 \alpha + \cos^2 \alpha \cdotp \cos^2 \alpha
E a questo punto utilizziamo sempre la prima relazione fondamentale della goniometria. Quando ci sono coseni e seni questa è la formula più utilizzata!
\sin^2 \alpha + \sin^2 \alpha \cdotp \cos^2 \alpha + \cos^2 \alpha \cdotp (1 - \sin^2 \alpha )
Svolgiamo la moltiplicazione:
\sin^2 \alpha + \sin^2 \alpha \cdotp \cos^2 \alpha + \cos^2 \alpha - \sin^2 \alpha \cdotp \cos^2 \alpha
E come possiamo vedere possiamo semplificare.
\sin^2 \alpha + \cos^2 \alpha
Qui è uscita fuori proprio la formula della prima relazione fondamentale della goniometria, che fa 1.
\sin^2 \alpha + \cos^2 \alpha = 1
E siamo arrivati al risultato dell’esercizio!
Continuiamo con altre identità goniometriche esercizi svolti!
Esercizio 4. 1 + \cos 2 \alpha = 2 -2 \sin^2 \alpha
Qui abbiamo un coseno di 2 alfa, e quindi non è un semplice coseno: utilizziamo allora la formula di duplicazione del coseno seguente.
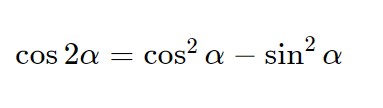
E sostituiamo nell’espressione chiaramente sempre del lato di sinistra.
1 + \cos^2 \alpha - \sin^2 \alpha
L’esercizio però, come potete vedere dal membro di destra della traccia, vuole tutto in seno. Quindi trasformiamo il coseno in seno utilizzando sempre la prima relazione della goniometria.
1 + ( 1- \sin^2 \alpha ) - \sin^2 \alpha
1 + 1- \sin^2 \alpha - \sin^2 \alpha = 2 - 2 \sin^2 \alpha
Ed abbiamo risolto.
Esercizio 5. \cos^6 \alpha + \sin^6 \alpha = 1 - 3 \cos^2 \alpha \sin^2 \alpha
Questo è un esercizio non facile, quindi potete anche passare più tardi di qui, potete anche andare ai prossimi esercizi e ritornarci. Comunque il trucco qui è scrivere il primo membro come:
( \cos^2 \alpha )^3+ (\sin^2 \alpha )^3
Ed utilizziamo la formula algebrica della somma di cubi:
A^3 + B^3 = (A+B)(A^2 -AB + B^2 )
dove nel nostro caso A=\cos^2 \alpha , B= \sin^2 \alpha
E quindi applichiamo la formula:
( \cos^2 \alpha + \sin^2 \alpha )(\cos^4 \alpha - \cos^2 \alpha \sin^2 \alpha +\sin^4 \alpha )
La prima parentesi fa 1 per via della prima relazione. Quindi ci rimane solo:
\cos^4 \alpha - \cos^2 \alpha \sin^2 \alpha +\sin^4 \alpha
Il coseno ed il seno alla quarta danno fastidio, perchè il risultato ha un grado di esponente di 2, quindi li scriviamo come:
\cos^2 \alpha \cos^2 \alpha - \cos^2 \alpha \sin^2 \alpha +\sin^2 \alpha \sin^2 \alpha
Ed utilizziamo sempre la prima relazione fondamentale per scrivere, il coseno in funzione del seno, e poi il seno in funzione del coseno nel secondo caso:
\cos^2 \alpha (1-\sin^2 \alpha ) - \cos^2 \alpha \sin^2 \alpha +\sin^2 \alpha (1-\cos^2 \alpha )
Svolgiamo le moltiplicazioni, sciogliendo le parentesi:
\cos^2 \alpha -\sin^2 \alpha \cos^2 \alpha - \cos^2 \alpha \sin^2 \alpha +\sin^2 \alpha -\cos^2 \alpha \sin^2 \alpha
E visto che \sin^2 \alpha + \cos^2 \alpha = 1
e sommando gli altri termini uguali otteniamo:
1 - 3 \cos^2 \alpha \sin^2 \alpha
Diciamo che in generale negli esercizi di identità goniometrica bisogna osservare il risultato (ossia il membro di destra) ed abbassare in generale il grado dell’espressione.
Abbiamo visto quindi come svolgere delle identità seno e coseno esercizi, adesso passiamo alla tangente e cotangente!
Continuiamo con altre identità goniometriche esercizi svolti!
Identità goniometriche esercizi svolti:
tangente e cotangente
Esercizio 6. \cos \alpha \tg \alpha + \sin \alpha \cotg \alpha =\cos \alpha +\sin \alpha
L’esercizio come potete vedere dal secondo membro vuole il tutto in seno e coseno, e quindi utilizziamo fin da subito le definizioni di tangente e cotangente. In generale è sempre una buona idea portare tutto in seno e coseno già dall’inizio. Ricordiamo la definizioni di tangente e cotangente:
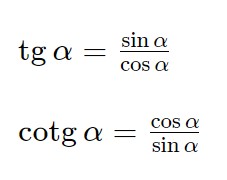
Quindi andiamo a sostituire sempre considerando solo il primo membro:
\cos \alpha \frac{\sin \alpha}{\cos \alpha} + \sin \alpha \frac{\cos \alpha}{\sin \alpha}
Andiamo a semplificare ed otteniamo:
=\cos \alpha +\sin \alpha
che è il risultato dell’esercizio, identità confermata!
Esercizio 7. (\tg \alpha + \cotg \alpha)\sin \alpha = \frac{1}{\cos \alpha}
Portiamo tutto in seno e coseno, utilizzando le definizioni.
( \frac{\sin \alpha}{\cos \alpha} + \frac{\cos \alpha}{\sin \alpha} )\sin \alpha
Andiamo a fare il minimo comune multiplo nella parentesi:
( \frac{\sin^2 \alpha + \cos^2 \alpha }{\cos \alpha \sin \alpha} )\sin \alpha
Il numeratore è 1, per via della prima relazione fondamentale.
( \frac{1 }{\cos \alpha \sin \alpha} )\sin \alpha
Poi andiamo a semplificare il seno col denominatore, ed otteniamo quindi:
\frac{1 }{\cos \alpha }
e ci troviamo!
Continuiamo con altre identità goniometriche esercizi svolti!
Esercizio 8. ( \cotg \alpha -\cos \alpha )\tg \alpha =1- \sin \alpha
Scriviamo il primo membro in termini di seno e coseno, con le definizione di tangente e cotangente:
( \frac{\cos \alpha}{\sin \alpha} -\cos \alpha ) \frac{\sin \alpha}{\cos \alpha}
E facciamo il minimo comune multiplo all’interno della parentesi tonda.
( \frac{\cos \alpha - \cos \alpha \sin \alpha }{\sin \alpha} ) \frac{\sin \alpha}{\cos \alpha}
E vediamo che possiamo mettere in evidenza il coseno a numeratore:
\frac{\cos \alpha (1 - \sin \alpha ) }{\sin \alpha} \frac{\sin \alpha}{\cos \alpha}
Ed andiamo a semplificare sia il coseno sia il seno, ottenendo:
1 - \sin \alpha
che è il secondo membro dell’identità!
Esercizio 9. \tg \alpha = \frac{ \tg \alpha -1 }{1- \cotg \alpha}
Negli esercizi di identità goniometrica, come potete vedere c’è una uguaglianza nelle tracce degli esercizi, quindi membro di sinistra deve essere uguale a quello di destra e viceversa. Ossia si può anche dimostrare che quello di destra sia uguale al membro di sinistra: possiamo anche partire da quello di destra quindi! Questo perchè con la sola tangente non ci facciamo nulla. E allora consideriamo:
\frac{ \tg \alpha -1 }{1- \cotg \alpha}
Visto che il risultato in questo caso è la tangente, dobbiamo trasformare tutto in tangente. Non usiamo in questo caso la definizione di tangente e cotangente in termini di seno e coseno, ma anzi utilizziamo la relazione seguente:
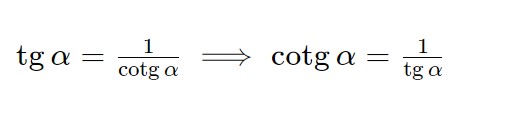
Andiamo quindi a scrivere in questo modo la contangente:
\frac{ \tg \alpha -1 }{1- \frac{1}{\tg \alpha } }
Facciamo il minimo comune multiplo al denominatore.
\frac{ \tg \alpha -1 }{ \frac{\tg \alpha - 1}{\tg \alpha } }
E portiamo questa frazione di frazione alla forma più semplice seguente:
\frac{ \tg \alpha -1 }{ \frac{\tg \alpha - 1}{\tg \alpha } }
( \tg \alpha -1 ) \frac{\tg \alpha}{\tg \alpha -1}
Semplificando, otteniamo il membro di sinistra ed abbiamo verificato l’identità!
= \tg \alpha
Esercizio 10. 2\cotg 2 \alpha + \tg \alpha = \cotg \alpha
Qui consideriamo il primo membro. Scriviamo la cotangente come l’inversa della tangente, come fatto nel precedente esercizio:
2 \frac{1}{\tg 2 \alpha } + \tg \alpha
Ed utilizziamo la formula di duplicazione della tangente, ossia:
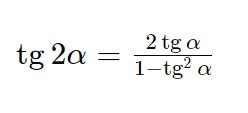
Ed andiamo a sostituire.
2 \frac{1}{\frac{2 \tg \alpha}{1- \tg^2 \alpha } } + \tg \alpha
2 \frac{1- \tg^2 \alpha}{2\tg \alpha } + \tg \alpha
Semplifichiamo il 2 ora.
\frac{1- \tg^2 \alpha}{\tg \alpha } + \tg \alpha
Ed andiamo ora a fare il minimo comune multiplo:
\frac{1- \tg^2 \alpha + \tg^2 \alpha }{\tg \alpha }
\frac{1 }{\tg \alpha } = \cotg \alpha
Continuiamo con altre identità goniometriche esercizi svolti!
Identità goniometriche esercizi con
secante e cosecante
Esercizio 11. 1 + \cotg^2 \alpha = \cosec^2 \alpha
Questo è semplice, giusto per introdurre queste due funzioni. Partiamo dal membro di sinistra: scriviamo la cotangente esplicitamente.
1 + \frac{\cos^2 \alpha}{\sin^2 \alpha}
Facciamo il minimo comune multiplo.
\frac{\sin^2 \alpha + \cos^2 \alpha}{\sin^2 \alpha}
Al numeratore abbiamo la prima relazione fondamentale, che fa quindi 1.
\frac{1}{\sin^2 \alpha}
A questo punto prendiamo la definizione di cosecante e secante:
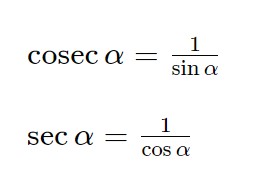
E quindi notiamo che:
\frac{1}{\sin^2 \alpha} = \cosec^2 \alpha
Esercizio 12. \cosec^2 \alpha + \sec^2 \alpha = \frac{1}{\cos^2 \alpha \sin^2 \alpha }
Qui l’esercizio, partendo dal membro di sinistra, vuole tutto in seno e coseno. Quindi utilizzando le definizioni di cosecante e secante, le scriviamo in funzione di seno e coseno:
\frac{1}{\sin^2 \alpha} + \frac{1}{\cos^2 \alpha}
E facciamo il minimo comune multiplo.
\frac{\cos^2 \alpha + \sin^2 \alpha}{\sin^2 \alpha \cos^2 \alpha }
Al numeratore abbiamo la prima relazione fondamentale, quindi abbiamo come risultato:
\frac{1}{\sin^2 \alpha \cos^2 \alpha }
E ci troviamo!
Continuiamo con altre identità goniometriche con esercizi svolti!
Esercizio 13. 2 \cosec 2 \alpha = \tg \alpha + \cotg \alpha
Partiamo da quello di destra qui, perchè se iniziate a fare i calcoli iniziare con quello di sinistra vi accorgete che è più complicato. Iniziamo a scrivere esplicitamente la tangente e cotangente usando le definizioni.
\frac{\sin \alpha}{\cos \alpha} + \frac{\cos \alpha}{\sin \alpha}
Facciamo il minimo comune multiplo, dando sempre uno sguardo al risultato a cui dobbiamo arrivare.
\frac{ \sin^2 \alpha + \cos^2 \alpha}{\cos \alpha \sin \alpha}
Al numeratore abbiamo la prima relazione fondamentale, che fa 1.
\frac{ 1}{\cos \alpha \sin \alpha}
A questo punto noi dobbiamo arrivare ad una 2 \cosec 2 \alpha
Notiamo che, se moltiplichiamo e dividiamo per 2, sbuca fuori la formula di duplicazione del seno.
\frac{ 2}{2 \cos \alpha \sin \alpha}
Utilizzando quindi la formula di duplicazione del seno:
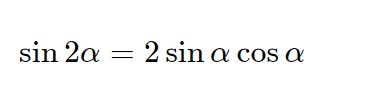
Otteniamo:
\frac{ 2}{\sin 2 \alpha}
A questo punto possiamo utilizzare la definizione di cosecante, e scrivere il risultato in cosecante:
= 2 \cosec 2 \alpha
E ci troviamo! Date sempre un occhio al risultato a cui dovete arrivare!
Esercizio 15. \frac{1- \cos^2 \alpha}{1 + \cotg^2 \alpha} = \frac{\sin^2 \alpha}{\cosec^2 \alpha}
Partiamo dal membro di sinistra, che c’è tanto su cui poter lavorare. Scriviamo la cotangente in funzione di seno e coseno:
\frac{1- \cos^2 \alpha}{1 + \frac{\cos^2 \alpha}{\sin^2 \alpha}}
E facciamo il minimo comune multiplo al denominatore.
\frac{1- \cos^2 \alpha}{ \frac{\sin^2 \alpha + \cos^2 \alpha}{\sin^2 \alpha}}
Chiaramente ciò che è uscito fa 1 per la solita prima relazione fondamentale.
\frac{1- \cos^2 \alpha}{ \frac{1}{\sin^2 \alpha}}
Portiamo questa frazione di frazione ad una forma decente come segue.
(1- \cos^2 \alpha)\sin^2 \alpha
La quantità in parentesi è:
\sin^2 \alpha = 1- \cos^2 \alpha
E quindi scriviamo tutto in seno, poichè il risultato che deve venire è in termini di seno, e in termini di cosecante (che a sua volta è funzione di seno). Quindi viene:
\sin^2 \alpha \sin^2 \alpha
Possiamo scrivere questa espressione con la forma equivalente di frazione di frazione:
\frac{\sin^2 \alpha}{\frac{1}{\sin^2 \alpha}}
Ed utilizzando ora la formula della cosecante otteniamo:
\frac{\sin^2 \alpha}{\cosec^2 \alpha}
Ossia il risultato!
Come risolvere esercizi identità goniometriche

Visto? Alla fine non erano così difficili, sarete pronti per la verifica in classe! Trovate altri esercizi svolti di altri argomenti di matematica che altro ancora!
Per approfondire: https://it.wikipedia.org/wiki/Identit%C3%A0_trigonometrica
Identità goniometriche esercizi svolti.
goniometriche
esercizi
goniometriche
elementari