Studio SEGNO funzione: 20 esercizi SVOLTI !
Studio SEGNO funzione: 20 esercizi SVOLTI ! Alla base dello studio delle funzioni c’è il dominio e poi la positività! Lo studio delle funzioni è un’argomento d’esame e di verifica in classe, quindi è importante esercitarsi su questo! Se non avete capito bene il dominio di una funzione, fate prima questi esercizi. Dopo aver studiato la positività il prossimo argomento sarà lo studio degli estremi e quindi la ricerca degli asintoti. In questa pagina ci saranno ben 20 esercizi svolti e spiegati passo dopo passo e con calma! Di seguito trovate l’indice della pagina. Iniziamo subito! Ricordiamoci che prima di iniziare lo studio della positività di ogni esercizio c’è bisogno di trovare il dominio prima che è alla base di un esercizio sulla funzione! Iniziamo!
Indice
- Riepilogo di tutte le funzioni
- Studio segno in: funzioni polinomiali
- Studio segno in: funzioni fratte
- Studio segno in: funzioni radici
- Studio segno in: funzioni logaritmiche
- Studio segno in: funzioni esponenziali
- Studio segno in: funzioni goniometriche
- Consigli generali per il calcolo del segno di qualsiasi funzione
Iniziamo subito con lo studio del segno di una funzione con esercizi svolti!
Riepilogo di tutte le funzioni


Iniziamo subito con lo studio del segno di una funzione con esercizi svolti!
Segno della funzione POLINOMIO
esercizi svolti
Esercizio 1. y= x^3-4x
Come prima cosa bisogna sempre calcolare il dominio della funzione. Il dominio di una funzione polinomiale è:
x \in \Reals
Se non vi ricordate i domini: vedete la pagina sul calcolo dei domini.
A questo punto calcoliamo il segno della funzione. Per fare questo dobbiamo sempre porre y \ge 0. In questo modo vedremo dove la funzione è positiva e dove è negativa e dove va ad intersecare l’asse delle x.
x^3-4x \ge0
Mettiamo in evidenza la x.
x( x^2-4) \ge 0
Per calcolarlo c’è bisogno di un falso sistema:
\big\| x\ge 0 \\ \big\| x^2 -4 \ge 0
\big\| x \ge 0 \\ \big\| x^2 \ge 4
\big\| x\ge 0 \\ \big\| x\le -2 \lor x\ge 2
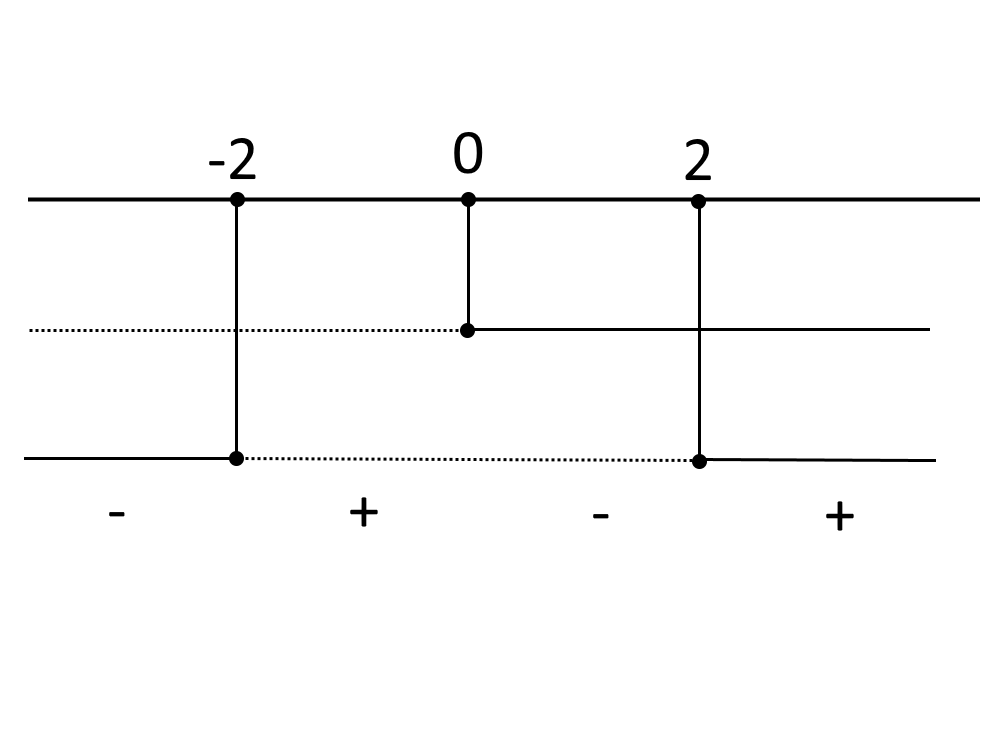
Prendiamo i valori positivi + perchè abbiamo un maggiore quindi:
-2 \le x \le 0 \land x \ge 2
Quindi la funzione in questi intervalli è positiva, ossia sta nella parte superiore del piano. In tutti gli altri intervalli la funzione sarà negativa, perchè la funzione è continua su tutto R. Cancelliamo quindi a penna tutte le zone in cui la funzione non sarà presente.
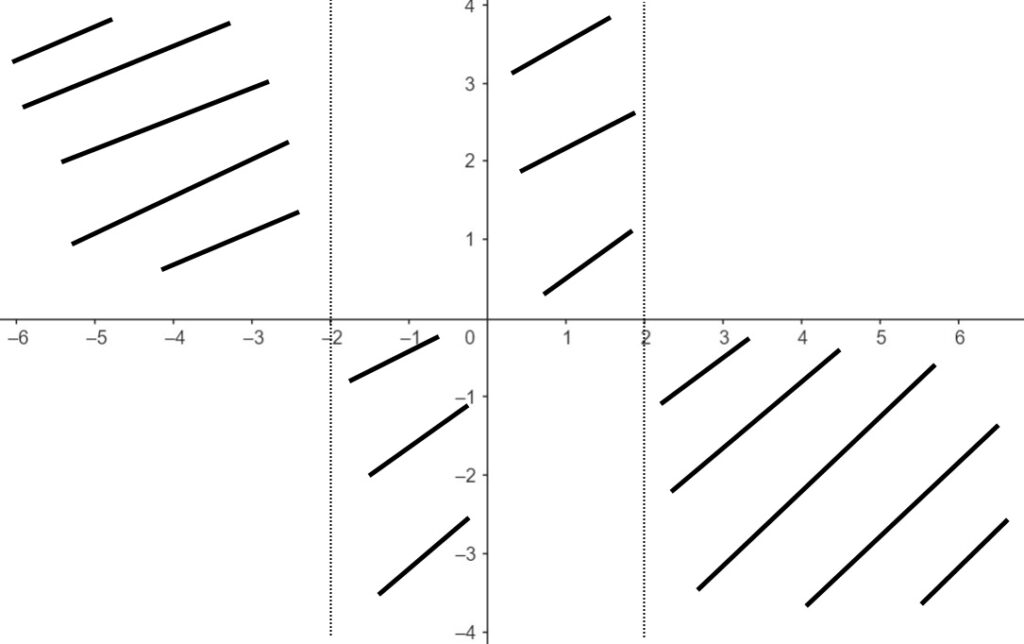
Di fatti la funzione fa come segue!
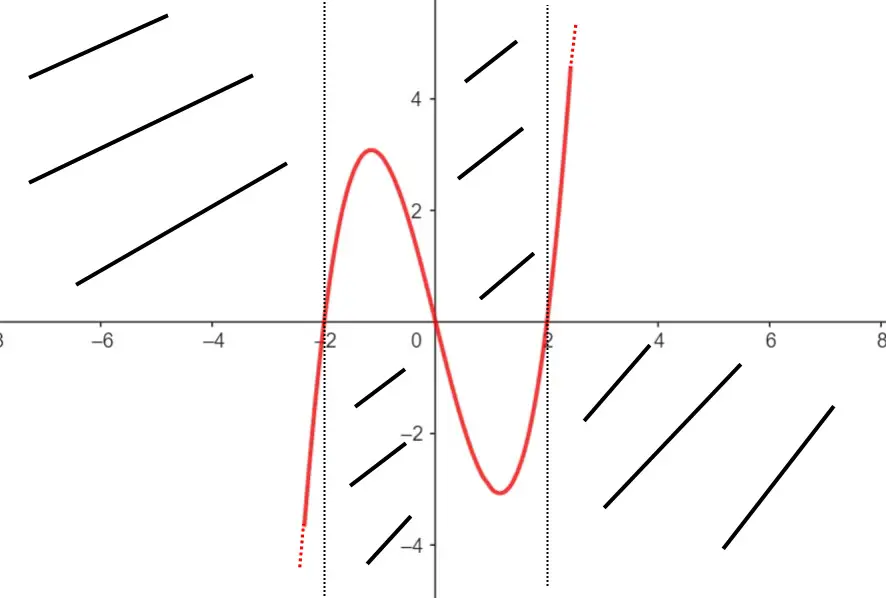
L’esercizio è così concluso, passiamo avanti!
Esercizio 2. y= x^2 -3x +1
Anche questa è una funzione polinomiale, ossia un polinomio, quindi ha il dominio su tutto R:
x \in \Reals
Adesso calcoliamoci il segno della funzione, e facciamo sempre lo stesso procedimento.
x^2 -3x +2 \ge 0
E’ un polinomio di secondo grado, calcoliamoci innanzitutto il Delta:
\Delta = b^2 -4ac = 9 - 8 = 1
Adesso calcoliamoci le due soluzioni:
x_{1,2}=\frac{3 \pm 1 }{2 }=2,1
E visto che abbiamo un maggiore o uguale, prendiamo le due soluzioni per valori esterni.
x \le 1 \land x \ge 2
E quindi in questi intervalli la funzione è positiva o uguale a zero e sta nella parte di sopra del piano. Negli altri la funzione sarà negativa.
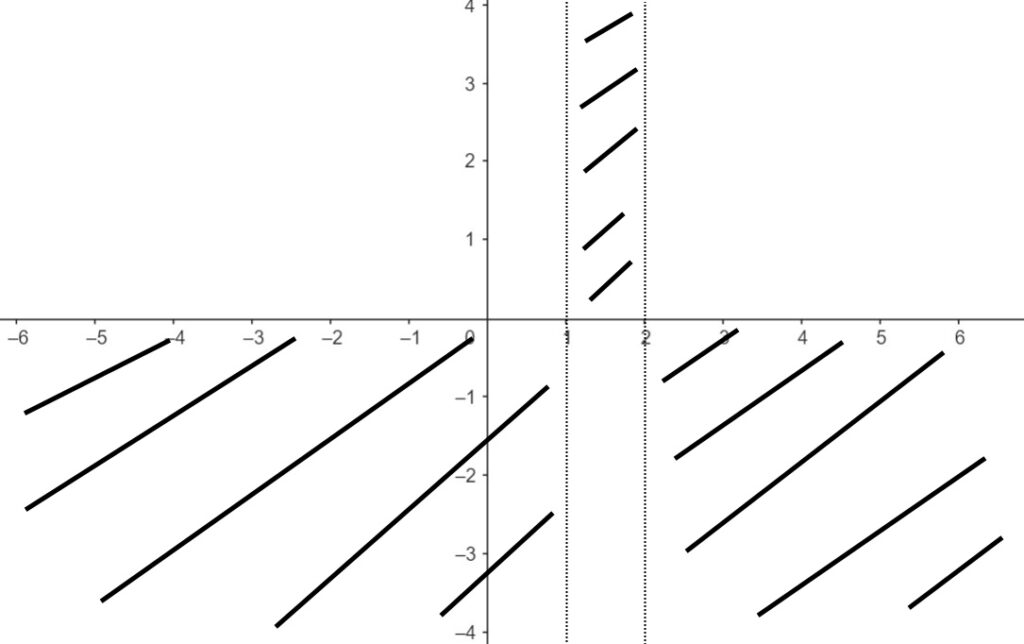
Esercizio 3. y= x^2 +1
Per il dominio non abbiamo problemi, è sempre: x \in \Reals
Poi studiamo il segno della funzione.
x^2 +1 \ge 0
x^2 \ge -1
Essendo x^2 sicuramente positivo o uguale a zero, sarà sempre più grande di -1. Quindi abbiamo che per qualsiasi x c’è soluzione della disequazione:
\forall x
Di fatti:
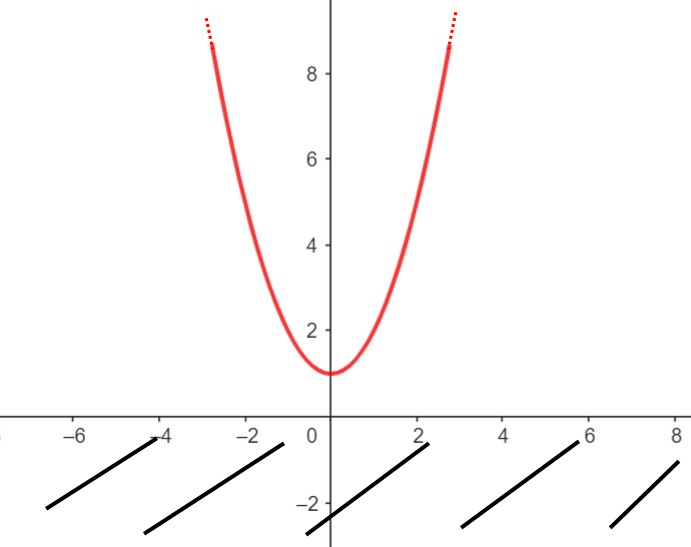
Continuiamo con lo studio del segno di una funzione con esercizi svolti!
Segno della funzione FRATTA
esercizi svolti
Esercizio 4. y=\frac{x-4}{x(1-x)^2 }
Iniziamo dal dominio della funzione fratta. Esso è denominatore diverso da zero.
x(1-x)^2 \ne 0
Sia il termine di sinistra che di destra devono essere diversi da zero.
x\ne 0 \land (1-x)^2 \ne 0
x\ne 0 \land x \ne 1
Adesso passiamo allo studio del segno della funzione.
\frac{x-4}{x(1-x)^2 } \ge 0
Lo risolviamo con un falso sistema. Ricordiamoci ovviamente che il denominatore non può essere uguale a zero, quindi giù va solo >.
\big\| x-4 \ge 0 \\ \big\| x(1-x)^2 > 0
\big\| x \ge 4 \\ \big\| x(1-x)^2 > 0
A sua volta il secondo termine lo risolviamo con un altro falso sistema.
\big\| x >0 \\ \big\| (1-x)^2 > 0
Il secondo termine di questo falso sistema è sempre positivo perchè c’è un quadrato, e non può essere uguale a zero per via del dominio, quindi:
\big\| x >0 \\ \big\| \forall x
E prendiamo i termini positivi, ed ha come soluzione x>0.
Sostituiamo questo risultato nel primo falso sistema.
\big\| x \ge 4 \\ \big\| x> 0
Che ha come soluzione, prendendo gli intervalli con il + totale:
x <0 \land x \ge 4
In questi intervalli la funzione è positiva, negli altri è negativa. Nel grafico mettiamo anche dei cerchi per indicare i punti dove la funzione non esiste, per via del dominio, ossia in: x=0 e x=1.
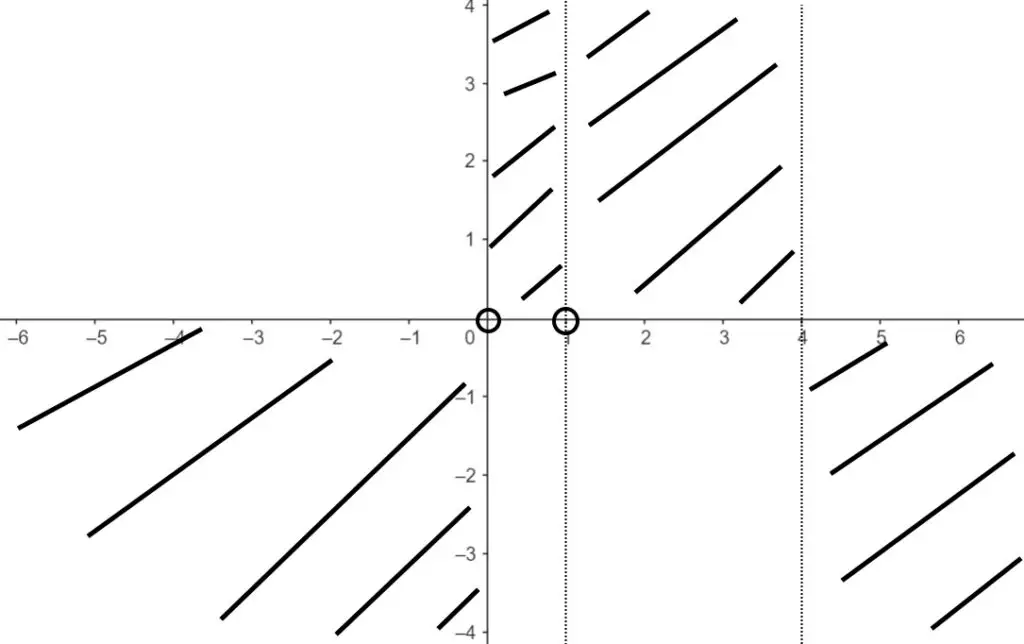
Per cui nelle funzioni fratte ci capiterà praticamente sempre di dover escludere solo dei singoli punti sull’asse.
Esercizio 5. y=\frac{x-1}{x-3}
Partiamo come sempre dal dominio: denominatore diverso da zero.
x-3 \ne 0 \implies x \ne 3
Iniziamo quindi a mettere un cerchietto in corrispondenza di x=3, per capire che la funzione non esiste in questo punto.
Ora passiamo allo studio del segno.
\frac{x-1}{x-3} \ge 0
E lo risolviamo con un falso sistema.
\big\| x-1 \ge 0 \\ \big\| x-3 > 0
\big\| x \ge 1 \\ \big\| x > 3
Dove prendiamo gli intervalli totali positivi (anche quelli con – e – perchè – per – fa +), quindi:
x <1 \land x > 3
Esercizio 6. y=\frac{x^2 -5x +4 }{x^2 -3x }
Partiamo come sempre dal nostro amato dominio:
x^2 -3x \ne 0
x(x -3) \ne 0 \implies x\ne 0 \land x \ne 3
Passiamo ora allo studio del segno.
\frac{x^2 -5x +4 }{x^2 -3x } \ge 0
Lo risolviamo con un falso sistema come sempre:
\big\| x^2 -5x +4 \ge 0 \\ \big\| x^2 -3x > 0
\big\| x^2 -5x +4 \ge 0 \\ \big\| x(x -3) > 0
Iniziamo dal calcolare il Delta del primo polinomio.
\Delta = 25-16=9
Calcoliamo le soluzioni di questo polinomio di secondo grado e poi andiamo per valori esterni, essendoci un maggiore.
x_{1,2}= \frac{5 \pm 3}{2}= 4,1
Quindi abbiamo:
\big\| x \le 1 \lor x \ge 4 \\ \big\| x(x -3) > 0
Per il secondo termine, facciamo un altro falso sistema.
\big\| x >0 \\ \big\| x -3 > 0
\big\| x >0 \\ \big\| x > 3
Di cui prendiamo gli intervalli col +, essendoci un maggiore, quindi:
x<0 \lor x>3
E lo uniamo al primo falso sistema iniziale.
\big\| x \le 1 \lor x \ge 4 \\ \big\| x<0 \lor x>3
Ed abbiamo come soluzione:
x<0 \land 1<x<3 \land x \ge 4
Continuiamo con lo studio del segno di una funzione con esercizi svolti!
Segno della funzione IRRAZIONALE
esercizi svolti
Esercizio 7. y=\sqrt{x-1}
Partiamo dal dominio: abbiamo un polinomio dentro che non ci dà problemi, e poi una radice. Il dominio di una radice è che l’argomento deve essere maggiore o uguale a zero, se indice è pari. Dominio:
x-1 \ge 0 \implies x \ge 1
Adesso passiamo allo studio del segno.
\sqrt{x-1} \ge 0
Una radice è sempre positiva o uguale a zero. Quindi nel dominio in cui la funzione esiste, essa sarà sempre al di sopra dell’asse delle x:
y \ge 0 sempre in x \ge 1
Ed abbiamo concluso l’esercizio.
Esercizio 8. y=\sqrt{\frac{x^2 -2x }{x^3 } }
Partiamo dal dominio: qui abbiamo una funzione radice ed una fratta. Per la fratta basta che il denominatore sia diverso da zero:
x^3 \ne 0 \implies x \ne 0
Per la radice, ciò che c’è dentro deve essere positiva o uguale a zero.
\frac{x^2 -2x }{x^3 } \ge 0
E lo risolviamo con un falso sistema.
\big\| x^2 -2x \ge 0 \\ \big\| x^3 > 0
\big\| x(x -2) \ge 0 \\ \big\| x > 0
Il primo lo risolviamo con un altro falso sistema:
\big\| x \ge 0 \\ \big\| x -2 \ge 0
\big\| x \ge 0 \\ \big\| x \ge 2
Che ha come soluzione, prendendo gli intervalli positivi:
x \le 0 \lor x \ge 2
Dove ricordandoci il primo dominio:
x < 0 \lor x \ge 2
E lo sostituiamo al falso sistema iniziale.
\big\| x < 0 \lor x \ge 2 \\ \big\| x > 0
Che ha come soluzione:
x \ge 2
e questo è il nostro dominio totale.
Passiamo ora allo studio del segno della funzione.
\sqrt{\frac{x^2 -2x }{x^3 } } \ge 0
La radice è sempre maggiore o uguale di zero. Basta che ciò che c’è dentro sia maggiore o uguale di zero, cioè basta che si verifica il dominio. Di fatti deduciamo che per x \ge 2 la funzione è sempre maggiore o uguale di zero.
Esercizio 9. y=\frac{ 2- |x| }{ \sqrt{x-1} }
Abbiamo una funzione fratta ed una funzione radice, iniziamo dal dominio della radice.
x-1 \ge 0 \implies x \ge 1
E poi passiamo al dominio della frazione:
\sqrt{x-1} \ne 0 \implies x \ne 1
Quindi unendo i due domini otteniamo un unico dominio: x>1.
Passiamo al segno della y.
\frac{ 2- |x| }{ \sqrt{x-1} } \ge 0
E lo risolviamo come sempre con un falso sistema.
\big\| 2- |x| \ge 0 \\ \big\| \sqrt{x-1} >0
La radice nel dominio è sempre positiva chiaramente.
\big\| |x| \le 2 \\ \big\| \forall x
\big\| -2 \le x \le 2 \\ \big\| \forall x
E prendiamo gli intervalli positivi:
-2 \le x \le 2
Ed uniamo a sua volta questa soluzione con il dominio x>1. Quindi otteniamo che la funzione y è positiva o uguale a zero nell’intervallo:
1 < x \le 2
Continuiamo con lo studio del segno di una funzione con esercizi svolti!
Segno della funzione LOGARITMICHE
esercizi svolti
Esercizio 10. y=\ln \frac{ x-1 }{x-4 }
Abbiamo una funzione logaritmo ed una razionale fratta. Calcoliamo prima il dominio di quella fratta:
x-4 \ne 0 \implies x \ne 4
E poi quello del logaritmo che è argomento >0.
\frac{ x-1 }{x-4 } > 0
Scriviamo il falso sistema per questa frazione.
\big\| x-1 > 0 \\ \big\| x-4> 0
\big\| x > 1 \\ \big\| x> 4
E ne ricaviamo come soluzione:
x<1 \land x> 4
che rappresenta proprio tutto il dominio della funzione.
Adesso passiamo allo studio del segno.
\ln \frac{ x-1 }{x-4 } >0
Sfruttiamo la relazione seguente:
\log_a b = x \implies b = a^x
che vale anche con i segni <>.
Quindi passiamo a:
\frac{ x-1 }{x-4 } > e^0
\frac{ x-1 }{x-4 } > 1
\frac{ x-1 }{x-4 } -1> 0
Facciamo il minimo comune multiplo.
\frac{ 3 }{x-4 } > 0
Il numeratore è positivo, quindi lo deve essere anche il denominatore:
Per x>4 abbiamo la funzione positiva o uguale a zero.
Addirittura notiamo che se poniamo y=0 non otteniamo soluzione, quindi per x>4 la funzione è solo maggiore di zero y>0.
Esercizio 11. y=\frac{ \ln x }{ \ln (x-1) }
Abbiamo due logaritmi ed una frazione razionale fratta. Partiamo dal dominio della fratta:
\ln (x-1) \ne 0
Ed utilizziamo la formula dell’esercizio precedente. Quindi segue che:
x-1 \ne e^0 \implies x-1 \ne 1 \implies x \ne 2
Adesso passiamo al dominio dei due logaritmi. Del primo al numeratore: x>0.
Del secondo: x-1>0 e quindi x>1.
Il dominio totale è:
x>1 \land x \ne 2
Ora studiamone il segno.
\frac{ \ln x }{ \ln (x-1) } \ge 0
E lo risolviamo con un falso sistema.
\big\| \ln x \ge 0 \\ \big\| \ln (x-1) >0
Usiamo per entrambi la formula di prima.
\big\| x \ge 1 \\ \big\| x-1>1
\big\| x \ge 1 \\ \big\| x>2
Che ha per soluzione gli intervalli positivi:
x<1 \lor x > 2
Ma ricordandoci che avevamo come dominio:
x>1 \land x \ne 2
Allora segue che la funzione è positiva nell’intervallo: x>2.
Mentre nell’altro 1<x<2 è negativa.
Esercizio 12. y=\sqrt{ \frac{ 1-4x^2 }{ \log_{\frac{1}{2}} x } }
Partiamo come sempre dal dominio. Abbiamo una funzione radice, una fratta ed un logaritmo. Partiamo dal logaritmo.
x>0.
Ora passiamo alla fratta, quindi denominatore diverso da zero:
\log_{\frac{1}{2}} x \ne 0
ed utilizziamo la solita formuletta che ci porta ad avere:
x \ne (\frac{1}{2})^0 \implies x \ne 1
Poi passiamo infine al dominio della radice.
\frac{ 1-4x^2 }{ \log_{\frac{1}{2}} x } \ge 0
Come sempre falso sistema, come vedete le cose si ripetono! Quindi basta esercitarsi che gli esercizi non sono poi così difficili! Ripetiamo sempre che il denominatore c’è solo >0 perchè non può essere uguale a zero, per il dominio!
\big\| 1-4x^2 \ge 0 \\ \big\| \log_{\frac{1}{2}} x > 0
Per il secondo termine usiamo la formuletta e ci dobbiamo ricordare che: quando la base è più piccola di 1 nella formula il segno si inverte! Quindi:
\log_a b > x \implies b<a^x
\big\| x^2 \le \frac{1}{4} \\ \big\| x<1
Il primo termine, essendo un minore, va per valori interni.
\big\| -\frac{1}{2} \le x \le \frac{1}{2} \\ \big\| x<1
E prendiamo come sempre i valori positivi nel disegnino:
-\frac{1}{2} \le x \le \frac{1}{2} \land x>1
Ed uniamo tutte le soluzioni ed otteniamo il dominio della funzione:
0 < x \le \frac{1}{2} \land x>1
Passiamo adesso allo studio del segno.
\sqrt{ \frac{ 1-4x^2 }{ \log_{\frac{1}{2}} x } } \ge 0
Una radice è sempre positiva o uguale a zero nel suo dominio, quindi otteniamo che questa funzione è sempre positiva o uguale a zero, nel suo dominio.
Continuiamo con lo studio del segno di una funzione con esercizi svolti!
Segno della funzione ESPONENZIALI
esercizi svolti
Esercizio 13. y=e^{\frac{\ln (x+1) }{ x} }
Per quanto riguarda il dominio di un esponenziale esso non dà problemi se la base è un numero. Qui la base è e e quindi non lo consideriamo proprio. Dobbiamo solo fare il dominio della frazione e del logaritmo. Per la frazione:
x \ne 0
E per il logaritmo:
x+1 >0 \implies x>-1
E quindi, unendo i due domini otteniamo un unico:
D: x>-1 \land x \ne 0
Passiamo ora allo studio del segno della funzione.
e^{\frac{\ln (x+1) }{ x} } \ge 0
Un’esponenziale è fatto in modo da essere sempre positivo. Ma mai uguale a zero. Quindi per ogni x del dominio si ha y>0.
Esercizio 14. y=\sqrt{ 2^{2x} +2 \cdotp 2^x -8 } - \sqrt{ 2^{x+1} +8 }
Abbiamo qui due radici, e varie funzioni esponenziali. Dobbiamo solo fare il dominio delle radici. Partiamo con la prima:
2^{2x} +2 \cdotp 2^x -8 \ge 0
Poniamo t=2^x
\implies t^2 +2t -8 \ge 0
E’ un polinomio di secondo grado, calcoliamo il Delta/quarti innanzitutto:
\frac{\Delta}{4}=1+8=9
Calcoliamo le due soluzioni e poi prendiamone i valori esterni, essendoci un maggiore.
t_{1,2}= -1 \pm 3 = 2,-4
t \le -4 \land t \ge 2
E quindi ritornando alla variabile iniziale:
2^x \le -4 \land 2^x \ge 2
2^x \le -4 non ha soluzione, perchè la funzione esponenziale è sempre positiva.
2^x \ge 2^1 \implies x \ge 1
Ora passiamo al dominio della seconda radice.
2^{x+1} +8 \ge 0 \implies 2 \cdotp 2^x +8 \ge 0
Dividiamo tutto per 2.
2^x +4 \ge 0 \implies 2^x \ge -4
Che è vero per tutte le x, essendo l’esponenziale positivo.
Quindi il dominio della funzione è:
x \ge 1
Passiamo ora al segno della funzione.
\sqrt{ 2^{2x} +2 \cdotp 2^x -8 } - \sqrt{ 2^{x+1} +8 } \ge 0
\sqrt{ 2^{2x} +2 \cdotp 2^x -8 } \ge \sqrt{ 2^{x+1} +8 }
Qui basta elevare tutto al quadrato e basta, visto che il dominio (cioè le condizioni di esistenza) le abbiamo già scritte.
2^{2x} +2 \cdotp 2^x -8 \ge 2^{x+1} +8
2^{2x} +2 \cdotp 2^x -8 \ge 2 \cdotp 2^x +8
Semplifichiamo e portiamo il -8 a secondo membro.
2^{2x} \ge 16
2^{2x} \ge 2^4
2x \ge 4 \implies x \ge 2
Finito!
Esercizio 15. y=(x+1)^{x-1}
Questa è una forma esponenziale del tipo:
f(x)^{g(x)}
Questa ha un dominio f(x)>0 ricordatevi!
D:x+1>0 \implies x>-1
Ora passiamo allo studio del segno della funzione.
(x+1)^{x-1} \ge 0
x+1 \ge 0 \implies x \ge -1
E quindi unendoci al dominio, abbiamo che la funzione è positiva per:
x>-1.
Continuiamo con lo studio del segno di una funzione con esercizi svolti!
Segno funzioni GONIOMETRICHE
esercizi svolti
Esercizio 16. y=2\sin x
Il dominio del seno è tutto R. Nello studio di una funzione ci si semplifica la vita, e si restringe il dominio nell’intervallo del periodo della funzione, nel nostro caso nell’intervallo: [0, 2 \pi ] .
Passiamo allo studio del segno.
2\sin x \ge 0
Questa vale se:
\sin x \ge 0
Notiamo che nel nostro intervallo di dominio, il seno è maggiore o uguale a zero nell’intervallo:
0 \le x \le \pi
Quindi in questo intervallo la funzione è al di sopra del piano cartesiano. Cioè ha ordinata positiva o uguale a zero.
Esercizio 17. y=\cos^2 x + 2 \cos x +1
Qui abbiamo dei coseni, quindi la funzione è definita in tutto R. Restringiamo però (lo possiamo fare perchè tanto la funzione è periodica) per comodità il dominio all’intervallo del periodo del coseno: [0,2 \pi ] .
Studiamo il segno della funzione.
\cos^2 x + 2 \cos x +1 \ge 0
Procediamo per sostituzione, e poniamo:
\cos x = t
t^2 + 2 t +1 \ge 0
Abbiamo una disequazione di secondo grado: calcoliamo innanzitutto il Delta, il Delta/quarti, come si preferisce, è uguale.
\Delta = 4-4=0
E poi calcoliamo le due soluzioni coincidenti:
t_{1,2} = \frac{-2 \pm 0 }{2}=-1
Un polinomio di secondo grado si può sempre scrivere come:
(t-t_1)(t-t_2) = (t+1)(t+1)=(t+1)^2
Quindi sostituendo questa relazione nella disequazione precedente otteniamo:
(t+1)^2 \ge 0
Ed essa, essendo un quadrato, è sempre positiva o uguale a zero.
Quindi la funzione è positiva \forall t \implies \forall \cos x
Ossia \forall x
La funzione è sempre positiva.
Esercizio 18. y=\sqrt{3} \sin x + \cos x
Il dominio è chiaramente tutto R. Nello studio delle funzioni periodiche e goniometriche si deve restringere l’intervallo in cui le si studia. Prendiamo come intervallo il periodo della funzione. Essendoci un seno e coseno, il periodo di tutta la funzione è sempre il periodo delle singole funzioni ossia: 2 \pi .
Quindi studiamo la nostra funzione nell’intervallo: [0,2 \pi ] .
Ora possiamo andare a studiarne il segno.
\sqrt{3} \sin x + \cos x \ge 0
Dividiamo tutto per 2, perchè andiamo a notare una cosa:
\frac{\sqrt{3}}{2} \sin x +\frac{1}{2} \cos x \ge 0
Ricordiamo che:
\frac{1}{2} = \sin \frac{\pi}{6}
\frac{\sqrt{3}}{2} = \cos \frac{\pi}{6}
E quindi:
\cos \frac{\pi}{6} \sin x + \sin \frac{\pi}{6} \cos x \ge 0
Ricordiamo la formula di addizione del seno:
\sin (\alpha + \beta) = \sin \alpha \cos \beta + \sin \beta \cos \alpha
Nel nostro caso allora otteniamo:
\sin (x+ \frac{\pi}{6} ) \ge 0
Chiamiamo: z= x+ \frac{\pi}{6}
\sin z \ge 0
Il seno è positivo o uguale a zero nell’intervallo:
0 \le z \le \pi
Ritorniamo alla variabile x iniziale risostituendo:
0 \le x+ \frac{\pi}{6} \le \pi
-\frac{\pi}{6} \le x \le \pi -\frac{\pi}{6}
-\frac{\pi}{6} \le x \le \frac{5\pi}{6}
Portiamo il primo pezzo nell’intervallo [0,2 \pi ] ed otteniamo:
0 \le x \le \frac{5\pi}{6} \land \frac{11\pi}{6} \le x \le 2 \pi
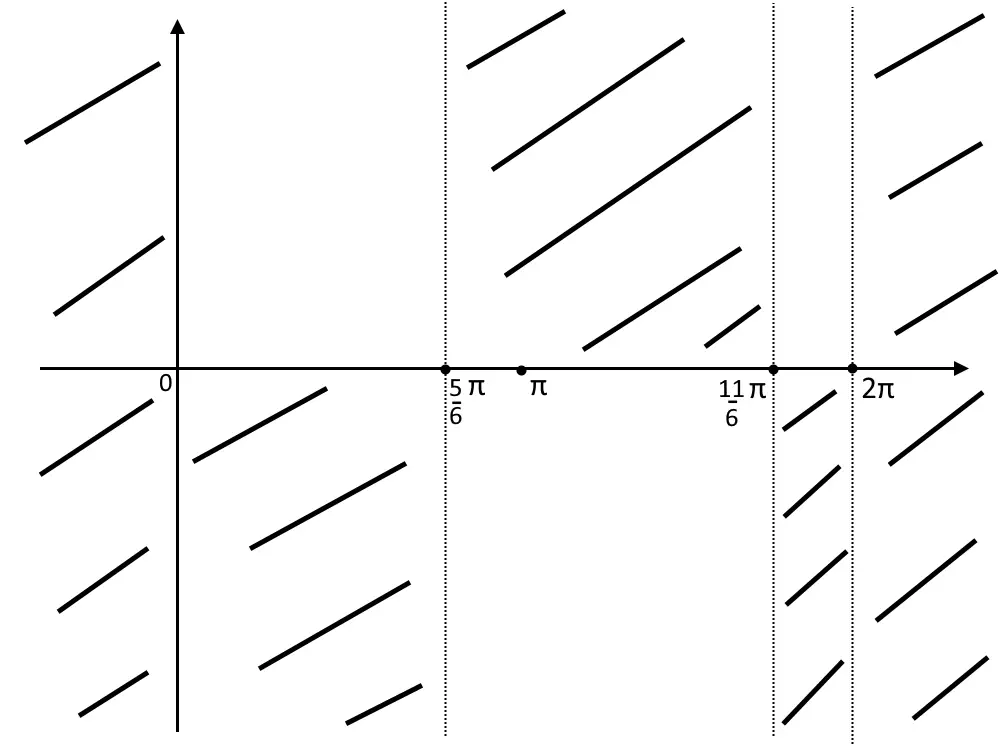
Esercizio 20. y=\cos x + \sin 2x
Il dominio del seno e coseno è facile:
x \in \Reals
Visto che il \cos x ha periodo 2\pi e \sin 2x ha periodo \pi allora il periodo di tutta la funzione è il periodo più grande delle singole funzioni, quindi 2\pi , quindi restringiamo all’intervallo [0,2 \pi ] lo studio della nostra funzione.
Come faccio a sapere il periodo della funzione sin 2x?
Una funzione periodica si scrive in generale come:
f(x)=A \sin (\omega x + \phi )
E questo vale anche per il coseno ecc. Il periodo si calcola con la formula:
T= \frac{2 \pi}{\omega}
Nel nostro caso:
T= \frac{2 \pi}{2} = \pi
Quindi concentriamoci nell’intervallo [0,2 \pi ] !
Passiamo subito al segno della funzione! Qui è utilissimo aver fatto le equazioni goniometriche! Bisognerebbe ripeterle!
\cos x + \sin 2x \ge 0
Utilizziamo la formula di duplicazione del seno ed otteniamo:
\cos x +2 \sin x \cos x \ge 0
Mettiamo in evidenza il coseno.
\cos x (1 +2 \sin x ) \ge 0
Risolviamo il tutto con un falso sistema.
\big\| \cos x \ge 0 \\ \big\| 1 +2 \sin x \ge 0
\big\| \cos x \ge 0 \\ \big\| \sin x \ge -\frac{1}{2}
Disegnando una circonferenza goniometrica capiamo dove il coseno è maggiore o uguale a zero e per quali angoli abbiamo il seno maggiore o uguale di -1/2.
Notiamo che il coseno è positivo o uguale a zero nell’intervallo di angoli:
0 \le x \le \frac{\pi}{2} \lor \frac{3 \pi}{2} \le x \le 2\pi
alla quale non si aggiunge la periodicità del coseno perchè siamo solo nell’intervallo [0,2 \pi ] !
Mentre il seno è maggiore o uguale di -1/2 per angoli:
0 \le x \le \frac{7 \pi}{6} \lor \frac{11 \pi}{6} \le x \le 2 \pi
Ricordo che se non sapete farli, è necessario ripetere le equazioni e disequazioni goniometriche!
Quindi ritorniamo e mettiamo questi risultati nel falso sistema di prima:
\big\| 0 \le x \le \frac{\pi}{2} \lor \frac{3 \pi}{2} \le x \le 2\pi \\ \big\| 0 \le x \le \frac{7 \pi}{6} \lor \frac{11 \pi}{6} \le x \le 2 \pi
E prendiamo i valori positivi, disegnando un segmento che va da 0 a 2 pigreco. Quindi:
0 \le x \le \frac{\pi}{2} \land \frac{7 \pi}{6} \le x \le \frac{3 \pi}{2} \land \frac{11 \pi}{6} \le x \le 2 \pi
Concludiamo questa pagina con dei consigli generali da seguire!
Consigli generali per il calcolo del segno di qualsiasi funzione

Continuate a studiare sul nostro sito per tanti altri esercizi di matematica che altro ancora!
Alla base dello studio di una funzione, è importantissimo partire dalle basi: quindi dominio di una funzione ! I prossimi step prevedono lo studio degli estremi, quindi bisogna saper fare i limiti, cliccate se ne avete bisogno! Anche forme indeterminate e limiti notevoli compariranno.
Per approfondire: https://it.wikipedia.org/wiki/Funzione_segno
codominio
asintoti
esercizi