Esercizi DOMINIO funzione
Esercizi DOMINIO funzione: 30 esercizi SVOLTI ! Il calcolo dei domini di una funzione è di fondamentale importanza sia per la verifica in classe sia soprattutto per l’esame finale in cui ci sarà lo studio di una funzione; è importantissimo sapere come calcolare il dominio di una funzione! In questa pagina vedremo ben 30 esercizi svolti e spiegati con calma passo dopo passo. All’inizio vedrete una tabella con tutte le funzioni che ci sono e che servono, ed alla fine troverete un riassunto di consigli da seguire per calcolare e sapere i domini delle funzioni al volo! Iniziamo subito e non badiamo alle chiacchiere!
Indice
- Tabella domini funzioni
- Calcolo dominio: funzioni polinomiali
- Calcolo dominio: funzioni fratte
- Calcolo dominio: funzioni radici
- Calcolo dominio: funzioni logaritmiche
- Calcolo dominio: funzioni esponenziali
- Calcolo dominio: funzioni potenza
- Calcolo dominio: funzioni goniometriche
- Consigli generali per il dominio di una funzione
Iniziamo subito con la tabella di tutte le funzioni !
Tabella dominio funzioni


Iniziamo subito!
Dominio di una funzione esercizi svolti:
funzioni POLINOMIO
Esercizio 1. y=x^3 -4x
Abbiamo di fronte una funzione polinomiale (cioè un polinomio), queste sono definite in generale come:
f: X \to Y
f: x\in \Reals \to \Reals
Quindi dalla seconda definizione possiamo capire che sono definite in un dominio (cioè dove esistono le x) in tutto l’asse! Cioè in tutto R. Non ci sono buchi: per qualsiasi x c’è sicuramente un valore della funzione f(x) o y. Se vi confondete ricordatevi che f(x)=y: la funzione la si può indicare in entrambi i modi!
Infatti il grafico di questa funzione è:
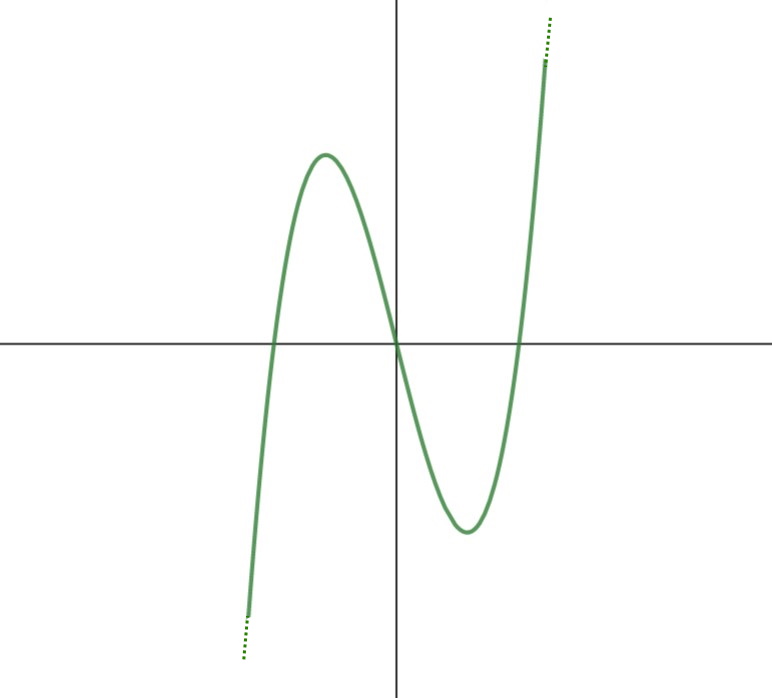
E potete notare bene che la funzione ha un valore per qualsiasi x prendiamo ! Il dominio infatti è semplicemente la parte dell’asse x in cui la funzione ha associato un valore.
Queste funzioni di soli polinomi non danno mai problemi per quanto riguarda il dominio. Quindi ogni volta che abbiamo un polinomio, sappiamo che il loro dominio, così come y=x^3 -4x , è sempre:
x\in \Reals cioè tutto l’asse x.
Esercizio 2. y=x^2 -1
Il discorso è lo stesso, quindi non ci dilunghiamo. La funzione è un semplice polinomio e basta, quindi è definita in tutto R.
La funzione x^2 -1 ha come dominio:
x\in \Reals cioè tutto l’asse x.
Continuiamo con gli esercizi dominio di una funzione !
Dominio funzioni FRATTE
esercizi svolti
Esercizio 3. y= \frac{x-1}{x^2 +3x}
Le funzioni razionali fratte sono definite in generale come la divisione di due funzioni:
y=\frac{N(x)}{D(x)}
In cui il dominio è tutto l’asse x, tranne i punti in cui D(x)\ne 0
In parole povere il denominatore deve essere sempre diverso da zero.
Nel nostro caso abbiamo una frazione di due polinomi che abbiamo detto essere definiti in tutto l’asse x, quindi non ci danno problemi. Il dominio della funzione fratta è dato dal porre diverso da zero il denominatore e prenderne tutte le soluzioni:
x^2 +3x \ne 0 \implies x(x+3) \ne 0
E quindi ricaviamo che:
x\ne 0 \land x \ne -3
Se fosse stato un normale esercizio avremmo scritto:
x\ne 0 oppure x \ne -3
Ma qui stiamo trovando il dominio che è un’altra cosa, quindi prendiamo tutte le soluzioni, scrivendo:
x\ne 0 ed x \ne -3
o come abbiamo scritto prima col simbolo
x\ne 0 \land x \ne -3
Il dominio della funzione razionale fratta \frac{x-1}{x^2 +3x} è quindi:
x\in \Reals - \{x=0,x=-3\}
Cioè tutto l’asse x tranne i punti x=0 e x=-3 che non vanno presi!
Infatti se andiamo a vedere il grafico, la funzione non ha nessun valore in questi punti.
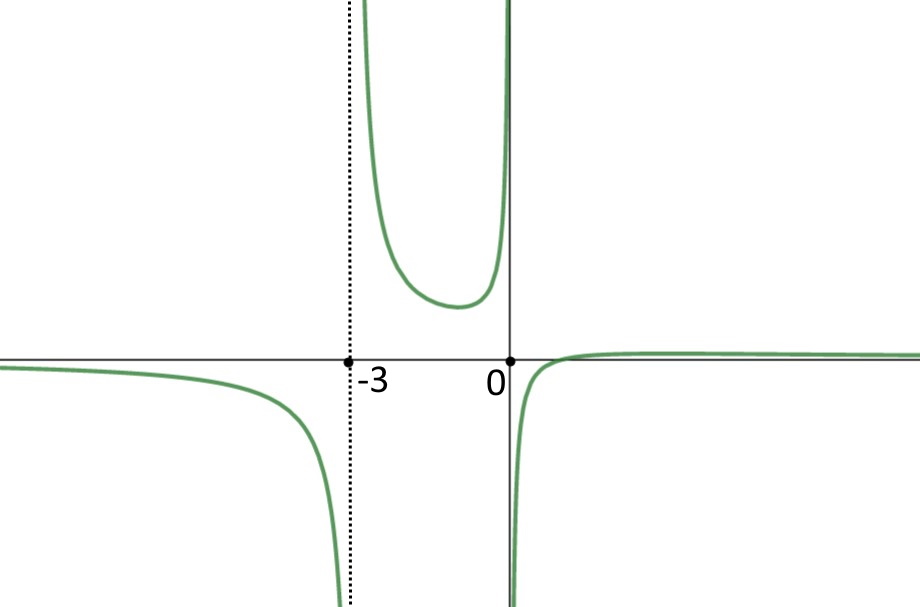
Esercizio 4. y=\frac{x +2 }{x^2 - 2x -8}
Anche in questo caso abbiamo una funzione razionale fratta, cioè una funzione che è una frazione. Questa funzione fratta è fatta di polinomi che sono definiti in tutto R, quindi no problem. L’unica cosa da fare allora è porre diverso da zero il denominatore:
x^2 - 2x -8 \ne 0
Questa è come se fosse una semplice equazione di secondo grado, ma con il diverso al posto dell’uguale, non cambia nulla.
\frac{\Delta }{4} = 1+8=9
x_{1,2} \ne \frac{1 \pm 3 }{1} = -2,4
Quindi x \ne -2 \land x \ne 4
Ed il dominio della funzione è tutto R tranne in questi punti.
x \in \Reals - \{x=-2,x=4\}
Esercizio 5. y=x^3 +2 + \frac{1}{x}
La funzione è fatta da una parte che è una funzione polinomiale che è definita in tutto R, e da una parte che è una funzione fratta. La parte polinomiale è definita in tutto R, no problem; mentre la parte razionale fratta sappiamo che dobbiamo porre il denominatore diverso da zero! Qui è semplicemente:
x \ne 0
Quindi il dominio di tutta la f(x) è:
x \in \Reals - \{x=0\}
Cliccate per altri esercizi extra sul dominio di una funzione fratta.
Dominio funzioni IRRAZIONALI
esercizi svolti
Esercizio 6. y=\sqrt{x}
La funzione radice è definita in generale come:
\sqrt{}: X \to Y
In cui se la radice è di esponente PARI:
\sqrt{}: x\ge0 \to y=\sqrt{x}
Cioè la parte dentro la radice deve essere uguale o maggiore di 0.
Se invece l’esponente della radice è DISPARI:
\sqrt{}: x\in \Reals \to y=\sqrt{x}
Cioè la funzione esiste per qualsiasi x.
Nel nostro esercizio abbiamo una radice con esponente pari e quindi dobbiamo porre la parte dentro la radice maggiore o uguale a zero.
Nel nostro caso abbiamo y=\sqrt{x}
E quindi x \ge 0
Il dominio della funzione è x \ge 0. E questo lo si può capire bene graficando la funzione radice.
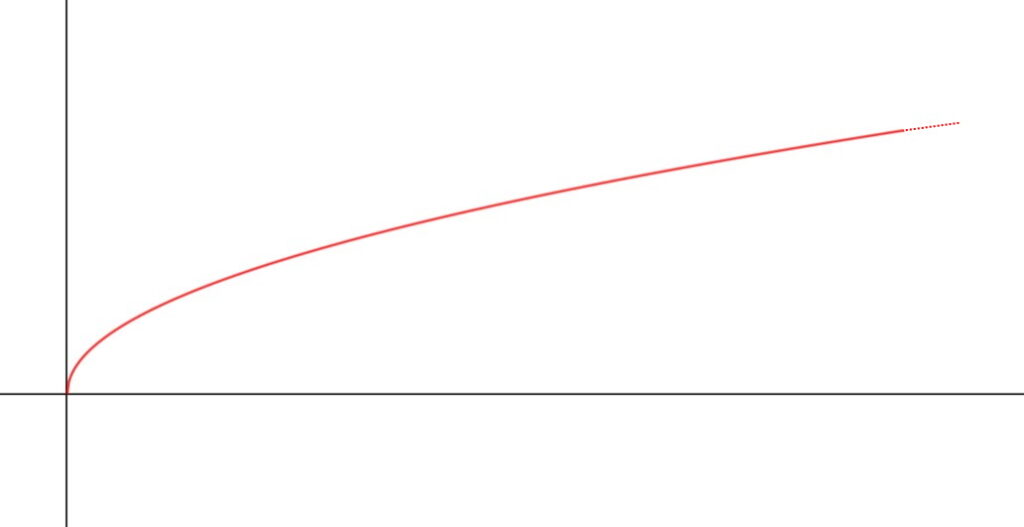
Esercizio 7. y=\sqrt{x^2-1}
Abbiamo una funzione radice in cui all’interno c’è un polinomio: il dominio del polinomio è tutto R, mentre il dominio della radice è dato dal porre la quantità dentro la radice maggiore o uguale a zero:
x^2-1 \ge 0 \implies x^2 \ge 1
La soluzione di questa disequazione ha valori esterni perchè c’è un maggiore, quindi:
x \le - \sqrt{x_1} \land x \ge + \sqrt{x_2}
Nel nostro caso:
x\le - 1 \land x \ge 1
Il dominio della nostra funzione è quindi:
x\le - 1 \land x \ge 1
Esercizio 8. y=\sqrt{\frac{x^2 -1}{x} }
Qui abbiamo una funzione radice ed una funzione fratta. Quando ci sono più funzioni insieme bisogna procedere dall’esterno all’interno. Cioè iniziamo dal dominio della radice: ciò che c’è dentro maggiore o uguale di zero (esponente pari).
\frac{x^2 -1}{x} \ge 0
Questa disequazione fratta la si risolve con un falso sistema.
\big\| x^2 -1 \ge 0 \\ \big\| x \ge 0
\big\| x^2 \ge 1 \\ \big\| x \ge 0
\big\| x\le -1 \lor x \ge 1 \\ \big\| x \ge 0
E devo prendere la parte positiva +, quindi:
-1 \le x \le 0 \land x \ge 1
Adesso passiamo alla funzione all’interno: funzione fratta. Per la funzione fratta sappiamo che il dominio è dato dal porre semplicemente il denominatore diverso da zero.
Qui quindi è semplicemente x \ne 0
Adesso dobbiamo unire le due soluzioni ed ottenere chiaramente un unico dominio di tutta la f(x).
-1 \le x \le 0 \land x \ge 1 \land x \ne 0
Il che significa levare il segno dell’uguale al primo termine perchè deve essere diverso da zero:
-1 \le x < 0 \land x \ge 1
Esercizio 9. y=\sqrt[3]{x^2 - 6x }
Non lasciatevi confondere! Qui abbiamo una radice con esponente dispari, che è definito in tutto R. All’interno poi abbiamo un polinomio che è definito anch’esso in tutto R, quindi il dominio di questa funzione è tutto R: non dobbiamo fare nulla!
x \in \Reals
Continuiamo con gli esercizi dominio di una funzione !
Dominio funzioni LOGARITMICHE
esercizi svolti
Esercizio 10. y= \log x
Abbiamo una funzione logaritmo, essa è definita in generale come:
\log : X \to Y
\log : x>0 \to \log x
Quindi capiamo che il dominio della funzione logaritmo è semplicemente ciò che c’è dentro il logaritmo maggiore di zero.
Nel caso y= \log x è semplicemente x>0, come vediamo dal grafico del logaritmo.
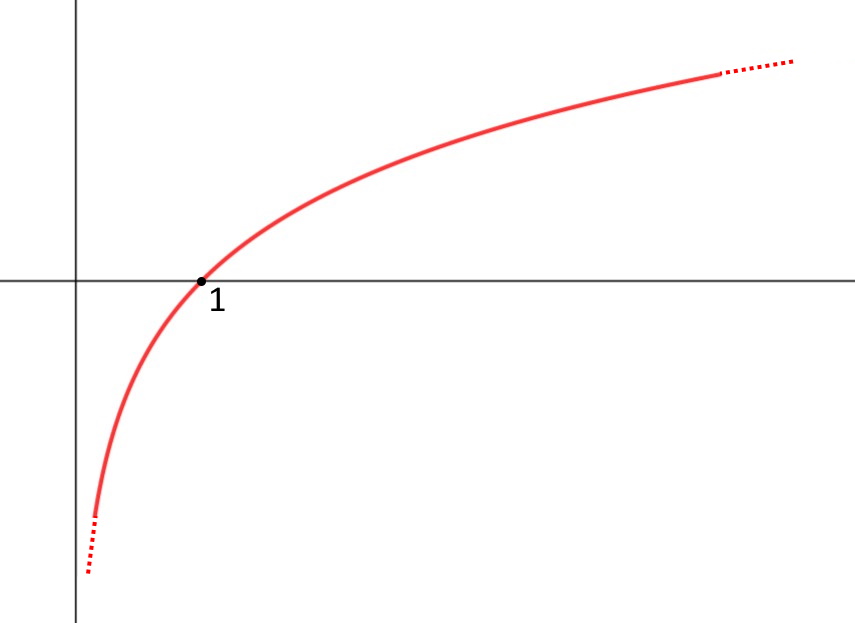
E ciò vale per qualsiasi sia la base del logaritmo !
Esercizio 11. y=\log (x+2)
Questa è una funzione logaritmo, in cui all’interno c’è una funzione polinomiale. Il polinomio è definito in tutto R: no problem! Invece per il logaritmo dobbiamo porre ciò che c’è dentro maggiore di zero ! Nel nostro caso:
x+2>0 \implies x>-2
Ed unito al dominio del polinomio che è tutto R, abbiamo che il dominio della funzione f(x) dell’esercizio è:
x>-2
Esercizio 12. y=\ln \sqrt{ \frac{1}{x-1} }
Abbiamo una funzione logaritmo, una funzione radice ed una funzione razionale fratta. Facciamo le cose con ordine e con calma ed iniziamo dall’esterno: funzione logaritmo.
Per la funzione logaritmo abbiamo detto che ciò che c’è all’interno, ossia l’argomento, deve essere maggiore di zero. Quindi:
\sqrt{ \frac{1}{x-1} } >0
Questa è una disequazione irrazionale; per far sì che essa sia maggiore di zero basta che ciò che c’è all’interno, ossia la frazione all’interno, sia maggiore di zero:
\frac{1}{x-1} >0
Ossa una disequazione fratta. Però qui non serve il falso sistema. Ragioniamo: 1 è maggiore di zero chiaramente sempre, quindi il denominatore dovrà essere positivo, perchè + diviso + farà +.
Quindi x-1>0 che implica x>1. Ed abbiamo fatto per quanto riguarda il dominio del logaritmo.
Passiamo adesso alla radice. Il dominio della radice è che la funzione all’interno deve essere maggiore o uguale di zero. Non serve rifarlo perchè già l’abbiamo fatto con una forma più restrittiva. Se non vi convince facciamo i conti lo stesso e vediamo. Calcoliamo il dominio della radice: funzione all’interno maggiore o uguale di zero.
\frac{1}{x-1} \ge 0
1 è già maggiore o uguale di zero, il denominatore invece deve essere solamente maggiore di zero come in un falso sistema.
Quindi come prima x-1>0 che implica x>1, che è la stessa cosa.
Passiamo alla funzione fratta adesso.
\frac{1}{x-1}
Per una funzione fratta il denominatore deve essere diverso da zero, quindi:
x-1 \ne 0 \implies x \ne 1
Uniamo le due soluzioni x>1 \land x \ne 1
ed otteniamo il dominio di tutta la funzione:
x>1.
Esercizio 13. y=\ln ( \ln x )
Non facciamoci spaventare e procediamo come sempre a strati. Partiamo dal logaritmo più esterno: abbiamo che l’argomento deve essere maggiore di zero:
\ln x >0
Essa è una disequazione logaritmica. Per trovare la x usiamo le formule seguenti:
Da \log_a b = c passiamo a b=a^c e questo vale anche con < o >.
Quindi nel nostro caso:
passiamo da \ln x >0 a x> e^0
e quindi x>1.
Ora passiamo al logaritmo più interno: argomento maggiore di zero, quindi solo x>0.
Uniamo le due soluzioni, per ricavare il dominio di tutta la funzione f(x).
x>1 \land x> 0
che sarebbe x>1.
Continuiamo con gli esercizi dominio di una funzione !
Dominio funzioni ESPONENZIALI
esercizi svolti
Esercizio 14. y= 3^{\frac{x-2}{x+2} }
Qui abbiamo una funzione esponenziale. Le funzioni esponenziali possono avere due forme:
- y=a^{f(x)} in cui basta calcolare il dominio normale della f(x) semplicemente, quindi non ci sono ulteriori restrizioni;
- y=f(x)^{g(x)} in cui c’è la restrizione che f(x)>0 deve essere positivo, e poi per g(x) si calcola il dominio normale.
Questo esercizio è della prima forma. Quindi del 3 non ce ne frega assolutamente nulla, ci calcoliamo semplicemente il dominio della funzione che sta come esponente, ossia \frac{x-2}{x+2} .
Essa è una funzione razionale fratta, quindi denominatore diverso da zero.
x+2 \ne 0 \implies x \ne -2
Ed abbiamo finito!
Esercizio 15. y=(1-2x)e^{-2x}
Questa è sempre una funzione esponenziale della prima forma, perchè (1-2x) non è elevato a nulla, lo è e invece.
(1-2x) è un polinomio che è definito in tutto R. Sul secondo abbiamo invece che l’esponente è la funzione: -2x che è anch’esso un polinomio e quindi definito su tutto R. Non abbiamo alcun tipi di restrizione: la funzione tutta è definita in:
x \in \Reals
Esercizio 16. y= (\frac{x+2}{x^2 -1} )^{ \sqrt{x} }
Questa è una funzione esponenziale della seconda forma scritta in precedenza. Quindi qui c’è, oltre i domini normali delle singole funzioni, anche la condizione che la base della potenza sia maggiore di zero, cioè:
\frac{x+2}{x^2 -1}>0
Questa disequazione fratta la si risolve con un falso sistema.
\big\| x+2 >0 \\ \big\| x^2-1 >0
\big\| x >-2 \\ \big\| x^2 >1
\big\| x >-2 \\ \big\| x<-1 \land x>1
Prendiamo i valori positivi, quindi:
-2<x<-1 \land x>1
Adesso passiamo al dominio della funzione fratta, denominatore diverso da zero.
x^2 -1 \ne 0 \implies x \ne \pm 1 che già è inclusa nel dominio precedente.
E poi abbiamo il dominio della radice, ossia ciò che c’è dentro maggiore di zero, quindi semplicemente x>0.
Uniamo le soluzioni ed otteniamo:
-2<x<-1 \land x>1 \land x>0
-2<x<-1 \land x>1
Continuiamo con gli esercizi dominio di una funzione !
Dominio di una funzione POTENZA
Le funzioni potenza sono funzioni del tipo: f(x)^\alpha , si distinguono 4 casi:
- \alpha intero positivo, come {1, 2, 3, 4…}, dominio semplice della f(x);
- \alpha intero negativo, come {-1, -2, -3…}, f(x) diverso da 0;
- \alpha razionale, come {\frac{1}{2}, \frac{1}{3}, \frac{4}{6} }, dominio normale;
- \alphairrazionale positivo, come {\sqrt{2}, \sqrt{3} ....}, f(x) \ge 0.
Esercizio 17. y=(x^2 +2x +1)^3
Questa è una funzione potenza del primo tipo, con dentro un polinomio. Il dominio di una funzione potenza di questo tipo è semplicemente il dominio della f(x) all’interno. Dobbiamo allora fare il dominio della funzione polinomio all’interno che è tutto R ! I polinomi non danno mai problemi!
x \in \Reals
Esercizio 18. y= ( \sqrt{x+2} )^{-3}
Questa è una funzione potenza del secondo tipo con all’interno una funzione radice. Abbiamo detto che il dominio di questa deve essere f(x) \ne 0 ma è ovvio! Perchè questa equivale a:
y= \frac{1}{(\sqrt{x+2})^3 }
cioè sarebbe una funzione fratta, per questo dobbiamo porre la funzione (denominatore) diversa da zero!
Partiamo quindi dal dominio della funzione fratta, denominatore diverso da zero.
(\sqrt{x+2})^3 \ne 0 \implies x+2 \ne 0 \implies x \ne -2
Poi passiamo al dominio della funzione radice:
x+2 \ge 0 \implies x \ge -2
Ed infine abbiamo al denominatore una funzione potenza (alla terza) che ha come dominio quello della funzione all’interno che abbiamo già fatto. Uniamo quindi le soluzioni:
x \ne -2 \land x \ge -2
x > -2
Esercizio 19. y=(x^2 -2 )^{\frac{3}{2} }
Questa è una funzione potenza del terzo tipo, anche qui non serve imparare nulla a memoria, perchè portiamo il tutto in una forma equivalente che già conosciamo:
y=(x^2 -2 )^{\frac{3}{2} }= \sqrt{(x^2 -2)^3 }
E questa funzione elevata ad un numero razionale sarebbe equivalente alla funzione f(x) con radice ed elevata ad una potenza (terza). Partiamo dall’esterno, dominio della radice:
(x^2 -2)^3 \ge 0 \implies x^2 -2 \ge 0
basterà che ciò che c’è dentro sia maggiore o uguale di zero, perchè un qualcosa elevato alla terza non dà la sicurezza che il numero venga positivo.
x^2 \ge 2
e ne prendiamo i valori esterni, essendoci un maggiore:
x \le - \sqrt{2} \land x \ge \sqrt{2}
Poi passiamo al dominio della funzione potenza all’interno: essendo del primo tipo, cioè elevato ad un numero intero positivo basterà calcolare solo il dominio della funzione interna. La funzione interna è un polinomio è quindi definita in tutto R. Il dominio totale allora sarà solo:
x \le - \sqrt{2} \land x \ge \sqrt{2}
Esercizio 20. y=( x^3 -1 )^{\sqrt{2}}
Abbiamo qui sopra una funzione potenza del quarto tipo, e dobbiamo quindi porre la funzione interna maggiore o uguale a zero.
x^3 -1 \ge 0 \implies x^3 \ge 1
\implies x \ge 1
Continuiamo con gli esercizi dominio di una funzione !
Dominio funzioni GONIOMETRICHE
esercizi svolti
Dominio funzioni seno e coseno
Esercizio 21. y=\sin x + \cos^2 x +2
Abbiamo in questo esercizio una funzione seno: definita in tutto R. Poi abbiamo una funzione coseno che si può riscrivere in maniera più ordinata come:
(\cos x )^2
Quindi traspare bene che abbiamo non solo una funzione coseno, ma anche una funzione potenza del primo tipo. Dobbiamo quindi calcolare solamente il dominio della funzione interna, ossia del coseno, che anch’essa definita su tutto R.
Il dominio è x \in \Reals.
Esercizio 22. y=\frac{\sin 2x }{\cos x -1}
Qui abbiamo una funzione razionale fratta, in cui all’interno vi sono funzioni seno e coseno: entrambe sono definite in tutto R. Quindi dobbiamo solo soffermarci sul dominio della funzione fratta: denominatore diverso da zero.
\cos x -1 \ne 0 \implies \cos x \ne 1
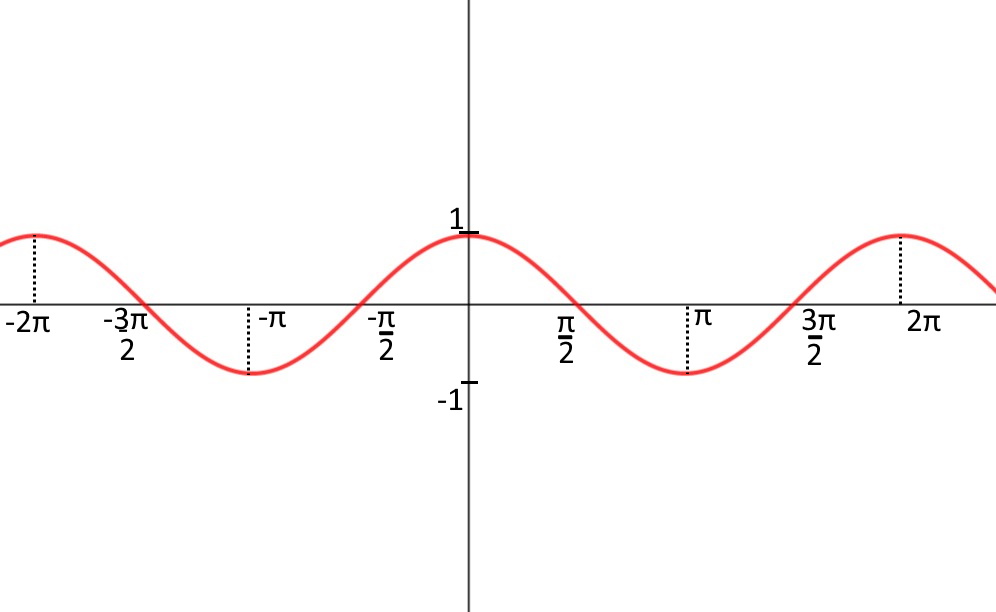
Essa una equazione goniometrica elementare (con disuguaglianza, ma è lo stesso procedimento). Vedendo il grafico del coseno, capiamo che esso assume come valore 1 solamente negli angoli:
x= 2\pi k con k numero intero.
Quindi il dominio è x\ne 2\pi k
Dominio funzioni tangente e cotangente
Esercizio 23. y=\frac{1}{\sin x } + \sqrt{ \tg x }
Da sinistra verso destra abbiamo: funzione razionale fratta, funzione seno, funzione radice, funzione tangente. Procediamo passo dopo passo, con calma.
Partiamo dalla prima, funzione seno: essa è definita su tutto R.
Passiamo alla seconda, funzione fratta: denominatore diverso da zero. Abbiamo le seguente equazione goniometrica elementare:
\sin x \ne 0 \implies x \ne k \pi con k numero intero.
Passiamo alla terza, funzione radice: ciò che c’è dentro maggiore o uguale di zero.
\tg x > 0
Questa invece è una disequazione goniometrica! Vediamo il grafico della tangente.
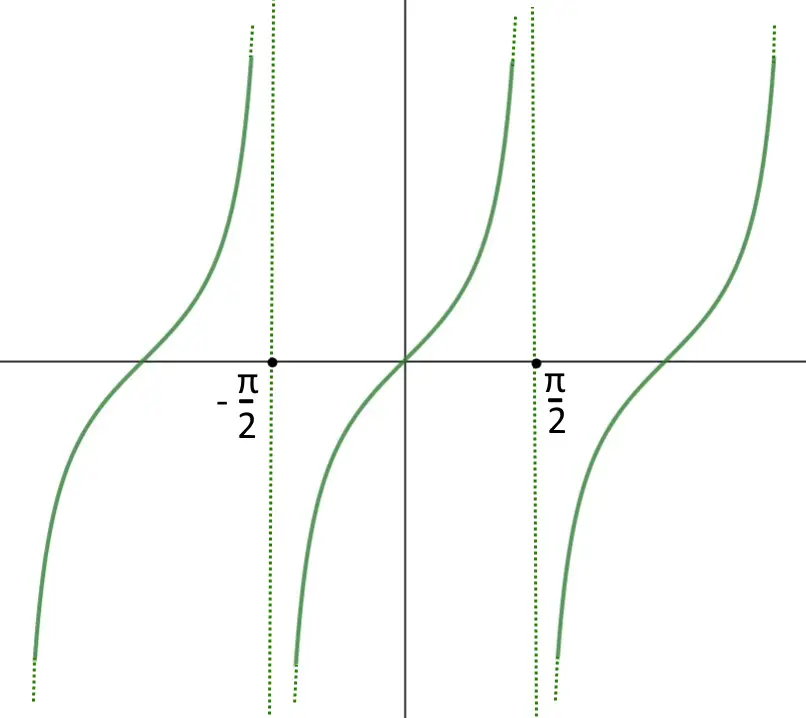
Notiamo che la tangente occupa la parte y>0 del piano cartesiano negli intervalli:
k\pi < x < \frac{\pi }{2} + k \pi
Infine passiamo alla quarta, funzione tangente definita per tutto R tranne nei punti in cui va ad infinito, ossia in:
x \ne \frac{\pi }{2} + k \pi
Uniamo tutte le soluzioni:
x \ne k \pi \land k\pi < x < \frac{\pi }{2} + k \pi \land x \ne \frac{\pi }{2} + k \pi
che sarebbe
k\pi < x < \frac{\pi }{2} + k \pi
Esercizio 24. y=(\cotg x )^{\sqrt{3}}
Partendo sempre dall’esterno verso l’interno troviamo: funzione potenza del quarto tipo, cioè con esponente irrazionale, e una funzione cotangente.
Partiamo dalla funzione potenza: base maggiore o uguale di zero come detto nel precedente capitolo.
\cotg x \ge 0
Per tale equazione goniometrica elementare vediamo il grafico della cotangente per capire il risultato.
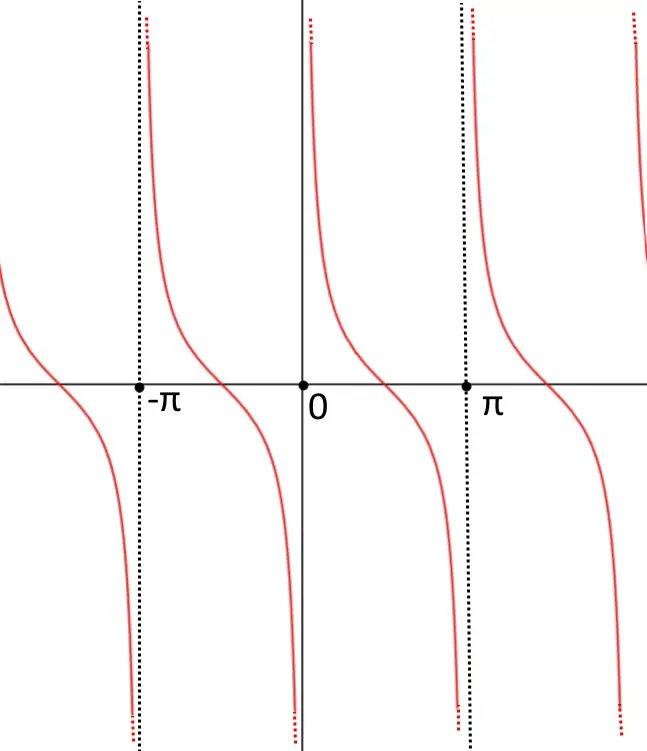
Capiamo che la cotangente è positiva o uguale a zero (cioè la parte in cui y>0) negli intervalli:
k \pi < x < \frac{\pi}{2} + k \pi
Passiamo adesso al dominio della cotangente: essa è definita in tutto R tranne nei punti dove va ad infinito, cioè in
x \ne k \pi
Unendo le soluzioni otteniamo il dominio totale:
k \pi < x < \frac{\pi}{2} + k \pi
Dominio funzioni arcoseno e arccoseno
Esercizio 25. y=\frac{1}{\arcsin \ln x}
Abbiamo partendo dall’esterno verso l’interno: funzione razionale fratta, funzione arcseno, funzione logaritmo.
Partiamo dalla funzione razionale fratta: denominatore diverso da zero.
\arcsin \ln x \ne 0
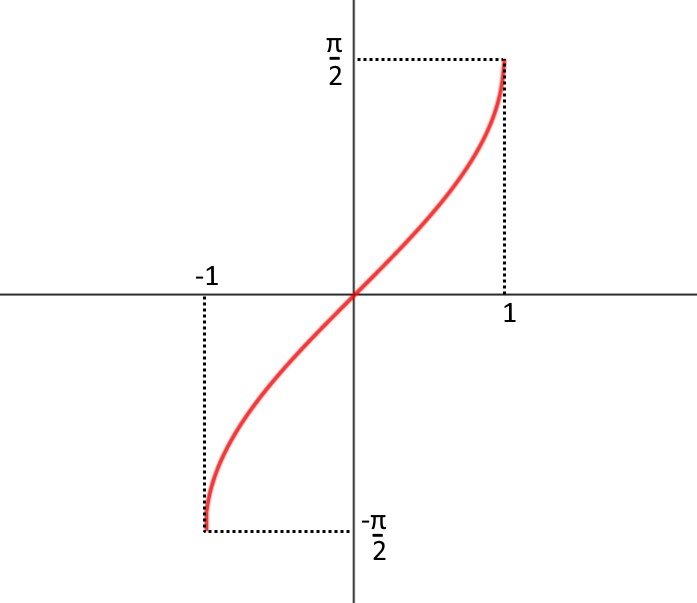
Vedendo il grafico notiamo che l’arcseno è uguale a zero solamente in 0. Ossia arcsen (0)=0 : tutto l’argomento dentro l’arcseno deve essere uguale a zero. Quindi:
\ln x \ne 0 \implies x \ne 1 visto come è fatto il logaritmo.
Passiamo alla seconda, funzione arcseno. Il dominio dell’arcseno è che l’argomento deve essere compreso fra 1 e -1. Quindi:
-1 \le \ln x \le 1
Calcoliamo una parte di disequazione alla volta. Ed utilizziamo la formula che collega logaritmo ad una potenza:
\log_a x = c e x= a^c
e questa formula vale con qualsiasi segno, anche con < o >.
\ln x \le 1 \implies x \le e^1 \implies x \le e
Ora passiamo all’altra disequazione.
\ln x \ge -1 \implies x \ge e^{-1}
E quindi ricaviamo (dominio arcseno) che la x è compresa in:
e^{-1} \le x \le e
Ed infine passiamo alla funzione logaritmo. Qui è semplice ed è x>0.
Adesso uniamo tutte le soluzioni:
e^{-1} \le x \le e \land x \ne 1 \land x>0
e^{-1} \le x \le e \land x \ne 1
Esercizio 26. y=\sqrt{\arccos x}
In questo esercizio abbiamo funzione radice e funzione arccoseno.
Partiamo dalla funzione radice. L’argomento deve essere maggiore o uguale a zero, quindi:
\arccos x \ge 0
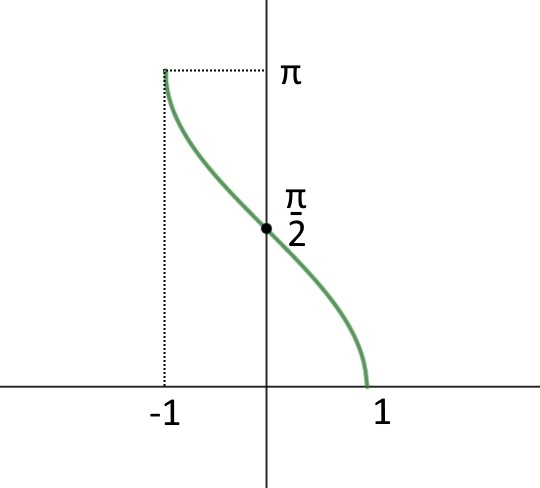
Vediamo dal grafico facilmente che l’arccoseno è sempre maggiore o uguale a zero, quindi per ogni x. No problem.
Passiamo all’arccoseno adesso, semplicemente anche’esso è definito fra -1 ed 1.
Quindi ricaviamo senza troppi problemi che il dominio della funzione dell’esercizio è:
-1 \le x \le 1
Abbiamo finito con gli esercizi dominio di una funzione: formuliamo adesso un riassunto e dei consigli da seguire!
Consigli generali per il dominio di una funzione

In questa pagina abbiamo visto come calcolare il dominio di una funzione qualsiasi. Potete continuare a studiare sulle nostre centinaia di esercizi svolti di matematica che altro ancora!
Per approfondire: https://it.wikipedia.org/wiki/Dominio_e_codominio#:~:text=In%20matematica%20il%20dominio%20e,un%20solo%20elemento%20del%20codominio.
Esercizi dominio funzione
continua
codominio