Forme INDETERMINATE limiti: 20 esercizi SVOLTI!
Forme INDETERMINATE limiti: 20 esercizi SVOLTI! Le forme indeterminate sono importantissime e compaiono spessissimo nelle verifiche in classe: è importante esercitarsi su questi! Se però non conoscete le basi del calcolo dei limiti, cliccateci sopra per capirne le proprietà base e come funzionano prima di passare a questa pagina! Dopo questa pagina ci saranno esercizi svolti sui limiti notevoli, che è l’ultimo step prima di sapere tutto sul calcolo dei limiti! Iniziamo subito!
Indice
- Forma indeterminata: + \infin - \infin
- Forma indeterminata: 0 \cdotp \infin
- Forma indeterminata: \frac{\infin }{\infin }
- Forma indeterminata: \frac{0}{0}
- Forme indeterminate: 0^0 , \infin^0 , 1^\infin
- E se abbiamo 0^\infin , \infin^\infin ?
- Consigli generali per la VERIFICA in classe.
Ogni forma indeterminata ha alcuni metodi di risoluzione da seguire. Iniziamo subito con il calcolo dei limiti sulle forme indeterminate!
Esercizi svolti forma indeterminata:
+ \infin - \infin
Esercizio 1. \lim\limits_{x \to + \infin } (x^4 -x^2 -9)
Notiamo subito che se andiamo a sostituire e a farne già il limite viene:
\lim\limits_{x \to + \infin } (x^4 -x^2 -9) = (+ \infin - \infin )
che è una forma indeterminata + \infin - \infin : ossia non possiamo capire il risultato esatto da questa forma, da questo risultato. Dobbiamo quindi escogitare qualche passaggio in più per ottenere un risultato esatto. Quando si ha questa forma indeterminata ed un polinomio si mette in evidenza il termine col grado più alto: nel nostro caso x^4 .
\lim\limits_{x \to + \infin } (x^4 -x^2 -9) = \lim\limits_{x \to + \infin } x^4 (1- \frac{1}{x^2} - \frac{9}{x^4} )
Dopo aver fatto ciò possiamo sostituire il termine alla quale la x tende. Quindi questo è l’unico passaggio in più che bisogna fare quando si ha un polinomio e questa forma indeterminata!
\lim\limits_{x \to + \infin } x^4 (1- \frac{1}{x^2} - \frac{9}{x^4} ) =+ \infin (1- \frac{1}{+ \infin} - \frac{9}{+ \infin} )
dove qualsiasi numero diviso per infinito fa zero. Quindi:
+ \infin (1- \frac{1}{+ \infin} - \frac{9}{+ \infin} ) = + \infin (1-0- 0) =+ \infin
Ed abbiamo risolto il limite! Nulla di così complicato!
Esercizio 2. \lim\limits_{x \to + \infin } (-2x^4 +x^3 -2x^2 )
Sostituiamo chiaramente sempre prima la x, per vedere che risultato esce fuori.
\lim\limits_{x \to + \infin } (-2x^4 +x^3 -2x^2 ) = (-\infin + \infin - \infin )
E’ una forma indeterminata + \infin - \infin , cioè somma di infiniti di diverso segno. Applichiamo lo stesso metodo dell’esercizio precedente per lo svolgimento: mettiamo in evidenza il termine con grado più alto: x^4.
\lim\limits_{x \to + \infin } (-2x^4 +x^3 -2x^2 ) = \lim\limits_{x \to + \infin } x^4 (-2 + \frac{1}{x} -\frac{2}{x^2} )
E sostituiamo!
\lim\limits_{x \to + \infin } x^4 (-2 + \frac{1}{x} -\frac{2}{x^2} ) = + \infin ( -2 + \frac{1}{+ \infin } -\frac{2}{+ \infin} ) =
= +\infin ( -2 +0 +0 ) = -2 \cdotp \infin = - \infin
Quindi quello che possiamo capire è che è il termine con grado più alto a dare il segno dell’infinito. Se il termine tende a infinito, è poi il coefficiente a determinarne il segno preciso. Ma comunque non sono mai cose da ricordare a memoria, semplicemente escono fuori naturalmente!
Esercizio 3. \lim\limits_{x \to - \infin } (-3x^3 +2x^2 -x )
Limite che tende ad un risultato di \lim\limits_{x \to - \infin } (-3x^3 +2x^2 +x ) = (\infin + \infin - \infin )
che è una forma indeterminata! Abbiamo un polinomio e quindi stesso procedimento! Mettiamo in evidenza il termine con grado più alto di esponente:
\lim\limits_{x \to - \infin } (-3x^3 +2x^2 -x ) =\lim\limits_{x \to - \infin } x^3 (-3 + \frac{2}{x}- \frac{1}{x^2} )=
=- \infin ( -3 +\frac{2}{- \infin}- \frac{1}{+ \infin } )= - \infin ( -3 +0+0)= -3 \cdotp (- \infin )= + \infin
In questo caso avevamo dei numeri divisi per – infinito, e fa sempre e comunque zero!
Continuiamo con altri esercizi forme indeterminate limiti!
Esercizio 4. \lim\limits_{x \to + \infin } (\sqrt{x+1} - \sqrt{x+2} )
Notiamo che sostituendo otteniamo la solita forma indeterminata:
\lim\limits_{x \to + \infin } (\sqrt{x+1} - \sqrt{x+2} ) =(\sqrt{\infin+1} - \sqrt{\infin+2} ) = \infin - \infin
visto che la radice di infinito (\sqrt{\infin} = \infin) tende ad infinito, e per capirlo basta vedere il grafico della funzione radice per capire come si comporta! Queste comunque sono le basi dei limiti che vi invito a vedere nel calcolo dei limiti.
Abbiamo adesso la stessa forma indeterminata, ma con delle radici. Il procedimento questa volta da seguire è di moltiplicare e dividere il tutto per le stesse radici cambiate di segno. In parole povere:
\lim\limits_{x \to + \infin } (\sqrt{x+1} - \sqrt{x+2} ) = \lim\limits_{x \to + \infin } (\sqrt{x+1} - \sqrt{x+2} ) \frac{(\sqrt{x+1} + \sqrt{x+2} )}{(\sqrt{x+1} + \sqrt{x+2} )}=
e sfruttiamo la relazione algebrica (a-b)(a+b) = a^2 -b^2 , dove a=\sqrt{x+1} , b= \sqrt{x+2} .
\lim\limits_{x \to + \infin } \frac{(\sqrt{x+1} - \sqrt{x+2} )(\sqrt{x+1} + \sqrt{x+2} )}{(\sqrt{x+1} + \sqrt{x+2} )}=\lim\limits_{x \to + \infin } \frac{\sqrt{x+1}^2 - \sqrt{x+2}^2}{(\sqrt{x+1} + \sqrt{x+2} )}=
=\lim\limits_{x \to + \infin } \frac{(x+1) -(x+2)}{(\sqrt{x+1} + \sqrt{x+2} )}=\lim\limits_{x \to + \infin } \frac{x+1-x-2}{(\sqrt{x+1} + \sqrt{x+2} )}=
Notiamo che la x a numeratore si semplifica. Possiamo adesso risolvere il limite.
=\lim\limits_{x \to + \infin } \frac{-1}{(\sqrt{x+1} + \sqrt{x+2} )}=\frac{-1}{ \sqrt{\infin} + \sqrt{\infin} }
dove chiaramente \infin +1 = \infin , \infin +2 = \infin .
Ed abbiamo come risultato del limite:
=\frac{-1}{\infin}=0
Anche in questo caso notiamo che le radici tendono ad infinito, quindi al denominatore abbiamo un infinito+ infinito che fa chiaramente +infinito.
Ricordatevi che la forma indeterminata è quando ho infiniti di diverso segno sommati fra di loro! Altrimenti
\infin + \infin = + \infin e -\infin -\infin = -\infin
La tattica generale delle forme indeterminate è quella di passare da un risultato che non possiamo conoscere esattamente ad uno il cui risultato è preciso e non indeterminato.
Esercizio 5. \lim\limits_{x \to + \infin } (\sqrt{x^2+1} - \sqrt{x^2-4} )
Anche questa è una forma indeterminata \infin -\infin ed abbiamo delle radici, quindi facciamo lo stesso procedimento di prima! Moltiplichiamo e dividiamo per una quantità che è la stessa del limite ma con segno opposto.
\lim\limits_{x \to + \infin } (\sqrt{x^2+1} - \sqrt{x^2-4} ) \frac{\sqrt{x^2+1} + \sqrt{x^2-4}}{\sqrt{x^2+1} + \sqrt{x^2-4}} = \lim\limits_{x \to + \infin } \frac{\sqrt{x^2+1}^2 - \sqrt{x^2 -4}^2}{\sqrt{x^2+1} + \sqrt{x^2-4}}
=\lim\limits_{x \to + \infin } \frac{x^2 +1 - (x^2- 4)}{\sqrt{x^2+1} + \sqrt{x^2-4}}=\lim\limits_{x \to + \infin } \frac{5}{\sqrt{x^2+1} + \sqrt{x^2-4}}=
Adesso sostituiamo e risolviamo il limite. Notiamo che la radice a +infinito tende a +infinito quindi al denominatore abbiamo un infinito + infinito:
=\frac{5}{\sqrt{\infin} + \sqrt{\infin}}=\frac{5}{\infin + \infin}=\frac{5}{\infin }=0
Ricordiamo che se non sapete per esempio che (\infin )^2 +1 = \infin allora fermatevi un attimo e studiate prima le basi dei limiti in calcolo dei limiti!
Esercizio 6. \lim\limits_{x \to - \infin } \frac{\sqrt{1-x} - \sqrt{1-2x}}{3x}
Abbiamo delle radici (non ci interessa che non abbiamo una radice al denominatore, basta che ci sono o al numeratore o al denominatore), e quindi sempre solito procedimento. Moltiplichiamo e dividiamo il tutto per \sqrt{1-x} + \sqrt{1-2x}
=\lim\limits_{x \to - \infin } \frac{\sqrt{1-x} - \sqrt{1-2x}}{3x} \frac{\sqrt{1-x} + \sqrt{1-2x}}{\sqrt{1-x} + \sqrt{1-2x} }=
=\lim\limits_{x \to - \infin } \frac{1-x - (1-2x)}{3x (\sqrt{1-x} + \sqrt{1-2x} ) }= \lim\limits_{x \to - \infin } \frac{x}{3x (\sqrt{1-x} + \sqrt{1-2x} ) }=
Come possiamo vedere la x si semplifica e quindi il denominatore non ci ha dato grossi problemi.
=\lim\limits_{x \to - \infin } \frac{1}{3 (\sqrt{1-x} + \sqrt{1-2x} ) }
Ed ora possiamo sostituire e risolvere facilmente questo limite.
= \frac{1}{3( \sqrt{\infin } + \sqrt{\infin } ) } = \frac{1}{3(\infin + \infin )} = \frac{1}{\infin} = 0
Continuiamo con altri esercizi sulle forme indeterminate limiti!
0 per INFINITO
Esercizio 7. \lim\limits_{x \to 0^+ } \sin 2x \cdotp \cotg x
Sostituendo e risolvendo il limite fin da subito notiamo che abbiamo una forma indeterminata: ossia un risultato che non possiamo determinare univocamente:
\lim\limits_{x \to 0^+ } \sin 2x \cdotp \cotg x = \sin 0^+ \cdotp \cotg 0^+ = 0 \cdotp \infin
questo poichè vediamo sempre i grafici del seno e della cotangente: il seno in un punto un poco dopo lo zero fa sempre zero, mentre la cotangente un pochetto dopo lo zero come possiamo vedere dal grafico tende a + infinito.
Se nella forma indeterminata del capitolo precedente ci sono delle regole generali da seguire, in questa non ce ne sono. Semplicemente si cerca di sfruttare formule trigonometriche e formule generali per cambiare la forma del limite, e cercare di trovare un risultato diverso!
Utilizziamo la formula di duplicazione e scriviamo \sin 2x = 2 \sin x \cos x e scriviamo la cotangente esplicitamente.
\lim\limits_{x \to 0^+ } \sin 2x \cdotp \cotg x = \lim\limits_{x \to 0^+ } 2 \sin x \cos x \cdotp \frac{\cos x }{\sin x }=
=\lim\limits_{x \to 0^+ } 2 \cos^2 x = 2 \cos^2 0^+ = 2
Come potete vedere è bastato scrivere il limite in una scrittura diversa per ottenere un risultato più preciso.
E se utilizzando questa formula ottenevamo sempre una forma indeterminata? Nessuno sa a priori cosa è giusto fare: quindi andate a tentativi, se non trovate un risultato esatto usate un’altra formula!
Esercizio 8. \lim\limits_{x \to \frac{\pi }{2} } \cos^2 x \cdotp \tg x
\lim\limits_{x \to \frac{\pi }{2} } \cos^2 x \cdotp \tg x = \cos^2 \frac{\pi }{2} \cdotp \tg \frac{\pi }{2} = 0 \cdotp \infin
Qui addirittura sulla tangente non conosciamo neanche il segno dell’infinito! Dobbiamo assolutamente trovare un altro risultato.
Scriviamo la tangente esplicitamente:
\lim\limits_{x \to \frac{\pi }{2} } \cos^2 x \cdotp \tg x =\lim\limits_{x \to \frac{\pi }{2} } \cos^2 x \frac{\sin x }{\cos x } =
Semplifichiamo il coseno:
= \lim\limits_{x \to \frac{\pi }{2} } \cos x \sin x = \cos \frac{\pi }{2} \sin \frac{\pi }{2} = 0 \cdotp 1 = 0
E’ bastato quindi scrivere la tangente esplicitamente e ottenere una semplificazione. Scrivere comunque tutto in termini di seno e coseno è quasi sempre una buona idea.
Continuiamo con altri esercizi forme indeterminate limiti!
Esercizio 9. \lim\limits_{x \to 0 } (2- \cotg x ) \tg x
\lim\limits_{x \to 0 } (2- \cotg x ) \tg x = (2- \cotg 0 ) \tg 0 = \infin \cdotp 0
Anche in questo caso abbiamo una forma indeterminata e anche in questo caso in zero non sappiamo se la cotangente tende a + infinito o – infinito!
Scriviamo allora sia la cotangente che la tangente in maniera esplicita.
\lim\limits_{x \to 0 } (2- \cotg x ) \tg x =\lim\limits_{x \to 0 } ( 2 - \frac{ \cos x }{ \sin x } ) \frac{ \sin x }{ \cos x } =
e poi spezziamo in due parti il limite:
= \lim\limits_{x \to 0 } 2 \frac{ \sin x }{ \cos x } - \lim\limits_{x \to 0 } \frac{ \cos x }{ \sin x } \frac{ \sin x }{ \cos x }=
I termini del secondo limite si semplificano, e ci rimane un 1 che è una costante:
=\lim\limits_{x \to 0 } 2 \frac{ \sin x }{ \cos x } - \lim\limits_{x \to 0 } 1= \lim\limits_{x \to 0 } 2 \frac{ \sin x }{ \cos x } -1
E svolgiamo il limite sostituendo la x:
=2 \frac{ \sin 0 }{ \cos 0 } -1 = 2\frac{ 0 }{ 1 } -1 = 0-1 = -1
visto che qualsiasi numero diverso da zero diviso per zero fa ancora zero.
Esercizio 10. \lim\limits_{x \to 1} \frac{2x^2 }{3 - 3x^2 } ( \sqrt{2-x} -1 )
\lim\limits_{x \to 1} \frac{2x^2 }{3 - 3x^2 } ( \sqrt{2-x} -1 ) =\frac{2 }{3 - 3} ( \sqrt{2-1} -1 ) = \frac{2}{0} (1-1)= \infin \cdotp 0
Ora vi spiegherò il procedimento da fare per ogni esercizio di questo tipo. Si va per tentativi con tutto ciò che si può fare. Vediamo che abbiamo una radice: quello che possiamo provare a fare è moltiplicare e dividere per la stessa quantità di radice cambiata di segno, come fatto nell’esercizio precedente:
\lim\limits_{x \to 1} \frac{2x^2 }{3 - 3x^2 } ( \sqrt{2-x} -1 ) = \lim\limits_{x \to 1} \frac{2x^2 }{3 - 3x^2 } ( \sqrt{2-x} -1 ) \frac{\sqrt{2-x} +1}{\sqrt{2-x} +1}=
=\lim\limits_{x \to 1} \frac{2x^2 }{3 - 3x^2 } \frac{2-x-1}{\sqrt{2-x} +1}=\infin \cdotp 0
Risolvendo il limite sostituendo otteniamo di nuovo la stessa forma indeterminata: quindi dobbiamo fare qualcos’altro, ciò che abbiamo fatto non è sufficiente ad ottenere un buon risultato. E allora mettiamo in evidenza il 3 al denominatore:
3 - 3x^2 = 3 (1- x^2 ) e sfruttiamo la relazione algebrica a^2 - b^2 = (a-b)(a+b)
3 (1- x^2 ) = 3 (1-x)(1+x) e ritorniamo al limite.
\lim\limits_{x \to 1} \frac{2x^2 }{3 (1-x)(1+x) } \frac{1-x}{\sqrt{2-x} +1}
E notiamo che ora è comparsa una semplificazione che possiamo fare, semplifichiamo quindi 1-x.
\lim\limits_{x \to 1} \frac{2x^2 }{3 (1+x) } \frac{1}{\sqrt{2-x} +1}
E ciò è sufficiente! Infatti sostituendo la x otteniamo:
= \frac{2 }{3 (1+1) } \frac{1}{\sqrt{2-1} +1}= \frac{2}{6} \frac{ 1}{2} = \frac{1}{6}
Ed abbiamo ottenuto un risultato super accettabile! Andate per tentativi e prima o poi riusciamo!
Continuiamo con altri esercizi sulle forme indeterminate limiti!
Esercizi svolti forma indeterminata:
\frac{\infin }{\infin }
Esercizio 11. \lim\limits_{x \to -\infin } \frac{x^6 -3x^4 }{2x^2 -2x +1 }
Sostituendo verifichiamo che questa è una forma indeterminata infinito/infinito:
\lim\limits_{x \to -\infin } \frac{x^6 -3x^4 }{2x^2 -2x +1 }= \frac{\infin - \infin }{\infin }
Questa forma indeterminata è la più semplice. Infatti l’unica cosa da fare è mettere sempre in evidenza il termine con grado più alto sia al numeratore che al denominatore:
\lim\limits_{x \to -\infin } \frac{x^6 -3x^4 }{2x^2 -2x +1 } =\lim\limits_{x \to -\infin } \frac{x^6 (1 -\frac{3}{x^2} }{x^2 (2 -\frac{2}{x} +\frac{1}{x^2} ) }
Possiamo semplificare x^2 con la x^6 al numeratore.
=\lim\limits_{x \to -\infin } \frac{x^4 (1 -\frac{3}{x^2} }{ 2 -\frac{2}{x} +\frac{1}{x^2} }
Poi abbiamo risolto il limite! Sostituiamo, e sapendo che ogni numero diviso infinito fa zero, abbiamo concluso l’esercizio!
=\frac{(-\infin)^4 (1 -\frac{3}{\infin} }{ 2 -\frac{2}{\infin} +\frac{1}{\infin} } =\frac{+\infin }{ 2 } =+\infin
Semplicissimo! Ed è sempre così!
Esercizio 12. \lim\limits_{x \to +\infin } \frac{3x^3 -4x^2 +6}{x^3 + 3x^2 -2x}
Anche questa è una forma indeterminata infinito / infinito: unica e sola cosa da fare è mettere in evidenza al numeratore ed al denominatore il termine con grado più alto.
= \lim\limits_{x \to +\infin } \frac{x^3 (3-\frac{4}{x} +\frac{6}{x^3})}{x^3 (1+ \frac{3}{x} -\frac{2}{x^2})}
Possiamo semplificare la x^3 nella frazione.
= \lim\limits_{x \to +\infin } \frac{3-\frac{4}{x} +\frac{6}{x^3}}{1+ \frac{3}{x} -\frac{2}{x^2}}
Ed ora possiamo sostituire e la sola cosa da ricordare è qualsiasi numero diviso per infinito tende a zero. Il segno non ci importa in questo caso perchè abbiamo uno zero sommato a qualcos’altro Quindi scrivere 0^\pm non serve.
= \frac{3-\frac{4}{\infin} +\frac{6}{\infin}}{1+ \frac{3}{\infin} -\frac{2}{\infin}} = \frac{3}{1}=3
Continuiamo con altri esercizi forme indeterminate limiti!
Esercizio 13. \lim\limits_{x \to + \infin } \frac{3x^3 +x^2 -2x}{2x^4 -x^2 }
Stessa forma indeterminata e stessa cosa da fare: mettere in evidenza il termine con grado di esponente più alto. Come vedete sono davvero semplici questi!
=\lim\limits_{x \to + \infin } \frac{x^3 (3+\frac{1}{x} -\frac{2}{x^2})}{x^4(2 -\frac{1}{x^2}) }
Semplifichiamo la x^3 !
=\lim\limits_{x \to + \infin } \frac{3+\frac{1}{x} -\frac{2}{x^2}}{x(2 -\frac{1}{x^2}) }
E poi possiamo già sostituire la x con infinito!
=\frac{3+\frac{1}{\infin} -\frac{2}{\infin}}{+\infin(2 -\frac{1}{\infin}) }=\frac{3}{+\infin}=0
Se volete essere precisi potete scrivere sicuramente 0^+, ma è uguale.
Esercizio 14. \lim\limits_{x \to -\infin } \frac{\sqrt{9x^4 +5x^2 +x}}{(x+2)^2}
Potrebbe spaventarci ma non deve, anche questo non è difficile e segue lo stesso procedimento degli altri. Qui però quello che possiamo vedere è che possiamo un attimo svolgere il quadrato al denominatore, perchè scritto non possiamo mettere in evidenza.
=\lim\limits_{x \to -\infin } \frac{\sqrt{9x^4 +5x^2 +x}}{x^2 + 4x +4}
Adesso possiamo mettere in evidenza il termine con grado più alto.
=\lim\limits_{x \to -\infin } \frac{\sqrt{x^4 (9+\frac{5}{x^2} +\frac{1}{x^3} ) } }{x^2 (1+ \frac{4}{x} +\frac{4}{x^2})}
Poi notiamo che possiamo portare x^4 fuori dalla radice, facendone la radice che diventa x^2.
=\lim\limits_{x \to -\infin } \frac{x^2 \sqrt{9+\frac{5}{x^2} +\frac{1}{x^3} } }{x^2 (1+ \frac{4}{x} +\frac{4}{x^2})}
Adesso ritorniamo ad un esercizio molto simile ai precedent: semplifichiamo la x^2 a numeratore e a denominatore:
=\lim\limits_{x \to -\infin } \frac{ \sqrt{9+\frac{5}{x^2} +\frac{1}{x^3} } }{1+ \frac{4}{x} +\frac{4}{x^2}}
E poi possiamo finalmente sostituire la x che tende a – infinito!
= \frac{ \sqrt{9+\frac{5}{-\infin} +\frac{1}{-\infin} } }{1+ \frac{4}{-\infin} +\frac{4}{-\infin}} = \frac{ \sqrt{9}}{1}
=\sqrt{9}=3
Ed abbiamo svolto l’esercizio!
Come prova del 9: basta vedere il grado dell’esponente più alto chi ce l’ha. Se numeratore e denominatore hanno lo stesso grado, a seguito di semplificazioni, avremo come abbiamo visto un numero finito; se il numeratore ha un grado dell’esponente più alto, allora dopo semplificazioni il denominatore sarà cancellato mentre il numeratore (che ha un grado più alto) tenderà ad infinito; se il denominatore ha un grado più alto, dopo semplificazioni sarà sopravvissuto solo il denominatore, e con x che tende ad infinito il limite tenderà a zero.
Continuiamo con altri esercizi sulle forme indeterminate limiti!
Limiti 0/0 esercizi svolti
Esercizio 15. \lim\limits_{x \to -5 } \frac{x^2 +3x -10}{x^2 -25 }
\lim\limits_{x \to -5 } \frac{x^2 +3x -10}{x^2 -25 } = \frac{25-15-10}{25-25}=\frac{0}{0}
Forma indeterminata di questo tipo viene trattata sempre allo stesso modo: scomporre in qualsiasi modo possibile il limite e cercare di semplificare i termini che rendono numeratore o denominatore 0.
Quindi guardando al limite possiamo notare che sia numeratore che denominatore si può scomporre e ricondurre ad una forma diversa. Al denominatore sfruttiamo la relazione algebrica:
a^2 - b^2 = (a-b)(a+b)
che nel nostro caso è x^2 - 25 = (x-5)(x+5)
Al numeratore abbiamo calcoliamo le soluzioni di x^2 +3x -10 =0
x_{1,2} = \frac{-3 \pm \sqrt{9+40} }{2} = -5,2
Le soluzioni di una equazione di secondo grado con discriminante positivo o uguale a zero può sempre essere scritto come:
x^2 +3x -10 = (x-x_1 ) (x-x_2 ) = (x+5)(x-2)
Sostituiamo il tutto nel limite.
\lim\limits_{x \to -5 } \frac{x^2 +3x -10}{x^2 -25 } = \lim\limits_{x \to -5 } \frac{ (x+5)(x-2)}{(x-5)(x+5) }
Come possiamo vedere abbiamo ottenuto una semplificazione di x+5, che ci fa avere una soluzione corretta del limite.
= \lim\limits_{x \to -5 } \frac{ x-2}{x-5 } = \frac{-5-2}{-5-5}=\frac{7}{10}
Questo è un po’ il metodo generale per calcolare i limiti 0/0 negli esercizi.
Esercizio 16. \lim\limits_{x \to 1 } \frac{x^3 -1}{x^4 -1}
Scomponiamo il fattore x^3 -1 tramite Ruffini. Il procedimento non verrà spiegato in questo esempio.
x^3 -1 = (x-1)(x^2 +x +1 )
Mentre il denominatore lo scomponiamo usando la relazione algebrica a^2 - b^2 = (a-b)(a+b)
Quindi x^4 -1 = (x^2 -1 )(x^2 +1 )
E riscomponiamo il termine x^2 -1 = (x-1)(x+1) con la stessa regoletta.
Otteniamo quindi:
\lim\limits_{x \to 1 } \frac{x^3 -1}{x^4 -1} =\lim\limits_{x \to 1 } \frac{(x-1)(x^2 +x +1 ) }{(x-1)(x+1)(x^2 +1 )}
Semplifichiamo x-1, e poi risolviamo il limite.
=\lim\limits_{x \to 1 } \frac{x^2 +x +1 }{(x+1)(x^2 +1 )} = \frac{1+1+1}{(1+1)(1+1)}=\frac{3}{4}
Forma indeterminata 0/0 con radici
Esercizio 17. \lim\limits_{x \to 9 } \frac{3- \sqrt{x} }{9-x }
\lim\limits_{x \to 9 } \frac{3- \sqrt{x} }{9-x } = \frac{0}{0}
Non si può scomporre nulla per il momento. L’unica cosa che si può fare, come abbiamo visto negli altri esercizi, è quella di moltiplicare e dividere per la stessa radice cambiata di segno. Almeno il limite prenderà una forma diversa e potrebbero comparire delle semplificazioni o scomposizioni da fare. Vediamo!
\lim\limits_{x \to 9 } \frac{3- \sqrt{x} }{9-x } =\lim\limits_{x \to 9 } \frac{3- \sqrt{x} }{9-x } \frac{3+ \sqrt{x} }{3+ \sqrt{x}}
e poi sfruttiamo la relazione algebrica a^2 - b^2 = (a-b)(a+b) dove a=3 e b=\sqrt{x}
E quindi:
=\lim\limits_{x \to 9 } \frac{9-x }{(9-x)(3+ \sqrt{x}) }
E’ comparsa una semplificazione!
=\lim\limits_{x \to 9 } \frac{1 }{3+ \sqrt{x} } = \frac{1}{3+\sqrt{9}}=\frac{1}{3+3}=\frac{1}{6}
Gli esercizi sulle forme indeterminate 0/0 con radici si svolgono praticamente sempre così!
Continuiamo con altri esercizi sulle forme indeterminate limiti!
Esercizi forme indeterminate:
0^0 , \infin^0 , 1^\infin
Esercizio 18. \lim\limits_{x \to 0^+ } (2x)^{\frac{2}{\ln 2x } }
\lim\limits_{x \to 0^+ } (2x)^{\frac{2}{\ln 2x } } = 0^{\frac{2}{\ln 0 }} = 0^{\frac{2}{- \infin }} = 0^0
Quando abbiamo una forma indeterminata di questo tipo oppure \infin^0 ,1^\infin il procedimento e le regole da seguire sono sempre le stessa ed è una sola.
Si sfrutta la relazione di uguaglianza:
a=e^{\ln a }
In questo modo si scrive il limite in una forma equivalente ma diversa ad occhio che ci porta ad un risultato che noi vogliamo.
Nella formula appena scritta a= tutto ciò che c’è nel limite, quindi per esempio nel nostro caso abbiamo:
\lim\limits_{x \to 0^+ } (2x)^{\frac{2}{\ln 2x } } = \lim\limits_{x \to 0^+ } e^{\ln a }= \lim\limits_{x \to 0^+ } e^{ \ln (2x)^{\frac{2}{\ln 2x } } }
Adesso semplifichiamo questa forma così complicata sfruttando alcune proprietà dei logaritmi molto semplici. Quando abbiamo che l’argomento del logaritmo è elevato a qualcosa allora vale:
\ln A^B = B \ln A
E nel nostro caso possiamo allora scrivere:
\ln (2x)^{\frac{2}{\ln 2x } } = \frac{2}{\ln 2x } \ln 2x = 2
Quindi il nostro limite si riduce a:
\lim\limits_{x \to 0^+ } e^2= e^2
ed abbiamo ottenuto un risultato che ci piace! E’ chiaro che non abbiamo cambiato il significato del limite. Ricordatevi sempre che una forma indeterminata è un risultato che è sconosciuto e che non possiamo calcolare precisamente. Ciò non significa che quel limite è incalcolabile, ma semplicemente che scritto così non dà risultati esatti. Quindi lo scriviamo in una forma equivalente utilizzando formule ecc. e dovremmo ottenere un risultato preciso.
Esercizio 19. \lim\limits_{x \to 0^+ } \frac{x}{2}^{ \frac{-3}{\ln x} }
\lim\limits_{x \to 0^+ } \frac{x}{2}^{ \frac{-3}{\ln x} } =0^{\frac{-3}{- \infin } }= 0^0
Il procedimento è sempre uguale, sfruttiamo la relazione di prima.
a=e^{\ln a } dove a è tutta la funzione interna del limite.
\lim\limits_{x \to 0^+ } \frac{x}{2}^{ \frac{-3}{\ln x} } =\lim\limits_{x \to 0^+ }e^{\ln \frac{x}{2}^{ \frac{-3}{\ln x} } }
Non dimenticatevi mai il simbolo del limite!
Adesso sfruttiamo invece la proprietà del logaritmo secondo la quale:
\ln A^B = B \ln A
Quindi nel nostro caso:
\ln \frac{x}{2}^{ \frac{-3}{\ln x} } = \frac{-3}{\ln x} \ln \frac{x}{2}
Adesso sfruttiamo un’altra proprietà importante del logaritmo che dice che:
\ln \frac{c}{d} = \ln c - \ln d
Quindi nel nostro caso che abbiamo \ln \frac{x}{2} allora possiamo scrivere:
\ln \frac{x}{2} = \ln x - \ln 2
E allora ritornando a prima:
\frac{-3}{\ln x} \ln \frac{x}{2} = \frac{-3}{\ln x} ( \ln x - \ln 2) = \frac{-3}{\ln x} \ln x - \frac{-3}{\ln x} \ln 2 = -3 + \frac{3\ln 2}{\ln x}
Quindi adesso sostituiamo ciò che abbiamo ricavato nel limite dell’esercizio.
\lim\limits_{x \to 0^+ }e^{\ln \frac{x}{2}^{ \frac{-3}{\ln x} } } = \lim\limits_{x \to 0^+ } e^{-3 + \frac{3\ln 2}{\ln x} }
E adesso siamo in grado di risolvere il limite.
=\lim\limits_{x \to 0^+ } e^{-3} e^{\frac{3\ln 2}{\ln x} } = e^{-3} e^{\frac{3\ln 2}{\ln 0^+}}=
= e^{-3} e^{\frac{3\ln 2}{\ln 0^+}}= e^{-3} e^{\frac{3\ln 2}{- \infin}}=e^{-3}e^0 = e^{-3} = \frac{1}{e^3}
Esercizio 20. \lim\limits_{x \to 0^+ } \frac{2}{x}^{\frac{1}{\ln x} }
\lim\limits_{x \to 0^+ } \frac{2}{x}^{\frac{1}{\ln x} } = \frac{2}{0^+}^{\frac{1}{\ln 0^+} }= +\infin^0
Anche questa forma indeterminata rientra nello stesso procedimento di quello precedente. Sfruttiamo la relazione di uguaglianza:
a=e^{\ln a }
Quindi:
\lim\limits_{x \to 0^+ } \frac{2}{x}^{\frac{1}{\ln x} } = \lim\limits_{x \to 0^+ } e^{\ln \frac{2}{x}^{\frac{1}{\ln x} } }
E adesso usiamo la regoletta del logaritmo:
\ln A^B = B \ln A
In pratica l’esponente va di fianco al logaritmo, quindi nel nostro caso:
\ln \frac{2}{x}^{\frac{1}{\ln x} } =\frac{1}{\ln x} \ln \frac{2}{x}
Come prima utilizziamo la proprietà del logaritmo seguente:
\ln \frac{c}{d} = \ln c - \ln d
E allora possiamo scrivere nel nostro caso:
\frac{1}{\ln x} \ln \frac{2}{x} = \frac{1}{\ln x} (\ln 2 - \ln x ) = \frac{1}{\ln x} \ln 2 - \frac{1}{\ln x} \ln x =
= \frac{\ln 2}{\ln x} - 1
Adesso che abbiamo una forma sufficientemente semplice, sostituiamo nel limite.
\lim\limits_{x \to 0^+ } e^{\ln \frac{2}{x}^{\frac{1}{\ln x} } } =\lim\limits_{x \to 0^+ } e^{ \frac{\ln 2}{\ln x} - 1 } =
Possiamo finalmente risolverlo ora.
=\lim\limits_{x \to 0^+ } e^{ \frac{\ln 2}{\ln x} } e^{-1} = e^{ \frac{\ln 2}{\ln 0^+} } e^{-1} =
=e^{ \frac{\ln 2}{- \infin} } e^{-1}= e^0 e^{-1}=e^{-1}=\frac{1}{e}
Continuiamo con altri esercizi forme indeterminate limiti!
Esercizio 21. \lim\limits_{x \to +\infin } (x+1)^{\frac{1}{\ln x} }
\lim\limits_{x \to +\infin } (x+1)^{\frac{1}{\ln x} } = \infin^0
Forma indeterminata sempre dello stesso tipo, sempre stesso procedimento! Sfruttiamo:
a=e^{\ln a }
Quindi nel nostro caso:
\lim\limits_{x \to +\infin } (x+1)^{\frac{1}{\ln x} } =\lim\limits_{x \to +\infin } e^{\ln (x+1)^{\frac{1}{\ln x} }}
Prendiamo da parte \ln (x+1)^{\frac{1}{\ln x} } ed utilizziamo la formula:
\ln A^B = B \ln A
Segue che:
\ln (x+1)^{\frac{1}{\ln x} } = \frac{1}{\ln x} \ln (x+1) = \frac{\ln (x+1) }{\ln x}
E a questo punto se proviamo a risolvere il limite notiamo che:
\lim\limits_{x \to +\infin } e^{\frac{\ln (x+1) }{\ln x}} = e^{\frac{\infin}{\infin}}
Non vi spaventate! Abbiamo adesso un’altra forma indeterminata: quella \frac{\infin}{\infin}. E se vi ricordate questa si risolve sempre allo stesso modo, cioè mettendo in evidenza il termine con grado più alto, nel nostro caso è x sia al numeratore che al denominatore. E visto che il polinomio è dentro al logaritmo, mettiamo in evidenza dentro al logaritmo.
\lim\limits_{x \to +\infin } e^{\frac{\ln (x+1) }{\ln x}} = \lim\limits_{x \to +\infin } e^{\frac{\ln x(1+\frac{1}{x}) }{\ln x}}
Chiaramente al denominatore non posso mettere in evidenza nulla, perchè ho solo x.
Adesso sfruttiamo la proprietà del logaritmo:
\ln ab = \ln a +\ln b
Quindi nel nostro caso:
= \lim\limits_{x \to +\infin } e^{\frac{\ln x + \ln (1+\frac{1}{x}) }{\ln x}} =\lim\limits_{x \to +\infin } e^{\frac{\ln x }{\ln x} + \frac{\ln (1+\frac{1}{x})}{\ln x} }
Ed ora posso risolvere senza problemi il nostro limite.
=\lim\limits_{x \to +\infin } e^{1 + \frac{\ln (1+\frac{1}{x})}{\ln x} } = e^{1+ \frac{\ln (1+\frac{1}{\infin})}{\ln \infin} } =
= e^{1+0}=e^1 = e
Continuiamo con altri esercizi sulle forme indeterminate limiti!
E se abbiamo 0^\infin , \infin^\infin ?
Queste non rientrano nelle forme indeterminate, perchè rappresentano dei risultati esatti. Infatti:
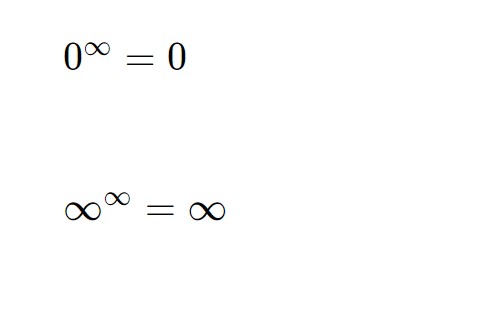
E adesso vediamo dei consigli per la verifica in classe o l’esame di stato: prendete un fogliettino e segnateveli!
Tutte le forme indeterminate

La lezione precedente è su esercizi sul calcolo generale dei limiti e le proprietà base dei limiti, mentre l’ultima che vi serve per sapere tutto sui limiti, sono i limiti notevoli.
Continuate a studiare sul nostro sito! Sia matematica che altro ancora!
Per approfondire le forme indeterminate:
https://it.wikipedia.org/wiki/Forma_indeterminata
svolti
limiti
limiti
notevoli