Esercizi SVOLTI integrali
Esercizi svolti INTEGRALI: 50 esercizi SVOLTI! Verifica in classe in arrivo sugli INTEGRALI? Eccovi ben 50 esercizi SVOLTI e SPIEGATI passo dopo passo e con calma! Con una giornata su questa pagina sarete pronti di già per il compito! Di seguito trovate l’indice che vi porta ai vari capitoli di questa pagina! Partiremo da un formulario delle formule più utili che vi serviranno nella verifica e poi calcoleremo tutti i tipi di integrali che si studiano al LICEO con vari tipi di difficoltà: facile, medio e difficili.
Indice degli esercizi SVOLTI integrali
- 0. Integrali IMMEDIATI
- 1. Integrazione per SOSTITUZIONE
- 2. Integrazione per PARTI
- 3. Integrali di funzioni RAZIONALI
- 4. Esercizi MISTI
- 5. Consigli e schema da seguire per affrontare QUALSIASI integrale
Tabella degli integrali IMMEDIATI

Iniziamo subito!
0. Esercizi svolti Integrali IMMEDIATI
Livello FACILE
Esercizio 1. \int 8 \sqrt{x}\;dx
La tabella degli integrali immediati è da imparare a memoria. L’intento della risoluzione degli integrali in generale è semplificarli mano mano fino ad arrivare ad un integrale immediato. Ricordate inoltre di mettere sempre per gli integrali indefiniti la costante integrativa c. Qui portiamo la costante 8 al di fuori dell’integrale. Poi, come sempre conviene fare, scriviamo la radice come un esponenziale: quindi elevato alla \frac{1}{2}:
\int 8 \sqrt{x}\;dx=8\int x^{\frac{1}{2}}\;dx
A questo punto siamo arrivati ad una forma tale che possiamo utilizzare l’integrale immediato:
\int x^\alpha \; dx =\frac{x^{\alpha + 1 }}{\alpha + 1} +c con \alpha \ne -1
Quindi nel nostro caso, visto che \alpha = \frac{1}{2} allora utilizzando la formula abbiamo che:
8\int x^{\frac{1}{2}}\;dx=8\frac{x^{\frac{1}{2} + 1 }}{\frac{1}{2} + 1} +c = 8\frac{x^{\frac{3}{2}}}{\frac{3}{2}} +c=
=8\cdotp \frac{2}{3} x^{\frac{3}{2}} +c = \frac{16}{3} x^{\frac{3}{2}} +c
Ed abbiamo svolto l’integrale!
Esercizio 2. \int \frac{1}{2x} dx
L’integrale immediato più simile è chiaramente:
\int \frac{1}{x} dx = \ln |x| + c
Non dimenticatevi di mettere il valore assoluto dentro il logaritmo in questo integrale immediato! Ritornando all’esercizio, possiamo notare che \frac{1}{x} è moltiplicato per \frac{1}{2} :
\int \frac{1}{2x} dx = \int \frac{1}{2} \cdotp \frac{1}{x}dx=
Come prima, portiamo la costante fuori dall’integrale.
= \frac{1}{2} \int \frac{1}{x}dx
A questo punto ci siamo ricondotti all’integrale immediato, utilizziamo quindi la formula.
= \frac{1}{2} \ln |x| + c
Esercizio 3. \int - \sin x \; dx
L’integrale è immediato, bisogna solo stare attenti al segno. Per non confondersi portiamo prima il segno – (che è una costante perchè sarebbe -1 che moltiplica l’integrale) fuori dall’integrale.
\int - \sin x \; dx =- \int \sin x \; dx
A questo punto utilizziamo la formula dell’integrale immediato seguente:
\int \sin x \; dx = - \cos x + c
Quindi sostituiamo.
- \int \sin x \; dx =- ( - \cos x )+ c = \cos x + c
Attenzione! La costante di integrazione c mettetela alla fine con +c e non fatela entrare mai nei calcoli.
Livello MEDIO
Esercizio 4. \int e^{2x} \; dx
Iniziamo adesso ad utilizzare gli integrali immediati con funzione f(x) al posto della sola x che abbiamo visto negli esercizi precedenti. In questo caso l’integrale alla quale ci riconduciamo è:
\int f'(x) \; e^{f(x)} \; dx=e^{f(x)} + c
Cioè dobbiamo far comparire la derivata di f(x) = 2x. La derivata è f'(x)=2. Quindi dobbiamo far comparire il 2. Questo lo facciamo moltiplicando e dividendo l’integrale per 2.
\int e^{2x} \; dx=\frac{1}{2}\int 2 \; e^{2x} \; dx
E ora utilizzando la formula ricordando che in questo caso la funzione di x è f(x) = 2x:
=\frac{1}{2}\int 2 \; e^{2x} \; dx=\frac{1}{2} e^{2x} + c
Esercizio 5. \int \frac{x+1}{x}dx
Qui non è immediatissimo l’integrale. Però un trucchetto da usare ( i trucchetti sono pochi e sono sempre gli stessi una volta imparati) è quello di spezzare la frazione. Una frazione può essere spezzata così:
\int \frac{x+1}{x}dx=\int [\frac{x}{x}+ \frac{1}{x}]dx=
Semplifichiamo ed otteniamo:
=\int [1 + \frac{1}{x}]dx = \int dx + \int \frac{1}{x}dx
Ed abbiamo ottenuto due integrali quindi. Due integrali però più semplici ed immediati. Per l’integrale \int dx usiamo la formula \int x^\alpha \; dx =\frac{x^{\alpha + 1 }}{\alpha + 1} +c e per il secondo integrale usiamo la formula
\int \frac{1}{x} dx = \ln |x| + c
Quindi viene semplicemente
\int dx + \int \frac{1}{x}dx= x+\ln |x| +c
Continuiamo con gli esercizi svolti di integrali!
Esercizio 6. \int \frac{\cos \sqrt{2x}}{\sqrt{x}} dx
Il coseno ci ricorda sicuramente l’integrale fondamentale seguente:
\int f'(x) \cos f(x) \; dx = \sin f(x) + c
Dobbiamo verificare se il coseno ha effettivamente la derivata al suo fianco. Scriviamo innanzitutto:
\int \frac{\cos \sqrt{2x}}{\sqrt{x}} dx = \int \frac{1}{\sqrt{x}} \cos \sqrt{2x} \; dx
Calcoliamo la derivata di ciò che c’è dentro il coseno, cioè della f(x) e vediamo la sua derivata quanto vale.
D (\sqrt{2x})=D(\sqrt{2} \sqrt{x})= \sqrt{2} \frac{1}{2 \sqrt{x}}
Noi nell’integrale abbiamo solamente \frac{1}{\sqrt{x}}, quindi per trovarci con tutta la derivata moltiplichiamo e dividiamo per \frac{\sqrt{2}}{2}.
\int \frac{1}{\sqrt{x}} \cos \sqrt{2x} \; dx=\frac{2}{\sqrt{2}} \int \frac{ \sqrt{2}}{2\sqrt{x}} \cos \sqrt{2x} \; dx
Ed ora applicando la formula ricaviamo:
=\frac{2}{\sqrt{2}} \sin \sqrt{2x} + c
Esercizio 7. \int e^x \; 5^{2e^x} dx
Questo integrale non deve spaventare. La forma di integrale immediato che si avvicina di più o comunque che si potrebbe avvicinare è:
\int f'(x) a^{f(x)} dx = \frac{1}{\ln a} a^{f(x)} + c
dove in questo caso a=5 e l’idea sarebbe di mettere come f(x) proprio l’esponente del 5: 2e^x. Alla base dobbiamo avere la sua derivata f'(x) = 2 e^x che è la stessa cosa, visto che la derivata di e^x fa sempree^x . Quindi moltiplichiamo e dividiamo per 2 ed il gioco è fatto!
\int e^x \; 5^{2e^x} dx = \frac{1}{2} \int 2e^x \; 5^{2e^x} dx
Applichiamo la formula appena detta ed abbiamo:
\frac{1}{2} \int 2e^x 5^{2e^x} dx = \frac{1}{2} \frac{1}{\ln 5} 5^{2e^x} + c
Livello DIFFICILE
Esercizio 8. \int \tg ^2 x \; dx
Prima di andare nel panico perchè non c’è nulla nella tabella simile alla tangente, ricordiamo che la tangente è definita come
\tg x = \frac{\sin x}{\cos x}
Quindi scriviamola per esteso:
\int \tg ^2 x \; dx=\int (\frac{\sin x}{\cos x})^2 dx =\int \frac{\sin ^2 x}{\cos ^2 x}dx
Dobbiamo lavorarci ancora su però. Partiamo SEMPRE dal numeratore. Ricordiamo che:
\sin ^2 x + \cos ^2 x =1 \implies \sin ^2 x = 1 - \cos ^2 x
Sostituiamo al numeratore il seno al quadrato.
=\int \frac{\sin ^2 x}{\cos ^2 x}dx =\int \frac{1 - \cos ^2 x}{\cos ^2 x}dx
A questo punto, come fatto prima, solito trucchetto: spezzare la frazione:
\int \frac{1 - \cos ^2 x}{\cos ^2 x}dx= \int \frac{1}{\cos ^2 x}dx - \int \frac{ \cos ^2 x}{\cos ^2 x}dx=\int \frac{1}{\cos ^2 x}dx - \int dx
Anche in questo caso abbiamo ottenuto due integrali, ma più semplici. Per il secondo non ci sono problemi perchè sappiamo che
\int dx = x +c mentre per il primo usiamo la formula dell’integrale immediato \int \frac{1}{\cos ^2 x}dx = \tg x +c
Quindi sostituiamo ed abbiamo risolto l’integrale!
=\tg x - x +c
Non dimenticatevi mai di scrivere il dx!
Esercizio 9. \int \frac{1}{\cos ^2 x \cdotp \sin ^2 x}dx
Quando vediamo un 1 e dei seni e coseni, ricordiamoci sempre che si può sfruttare la formula:
\sin ^2 x + \cos ^2 x =1
E sostituiamola nell’integrale!
\int \frac{1}{\cos ^2 x \cdotp \sin ^2 x}dx =\int \frac{\sin ^2 x + \cos ^2 x }{\cos ^2 x \cdotp \sin ^2 x}dx
Adesso, come prima, trucchetto già usato: spezziamo la frazione e l’integrale in due!
=\int \frac{\sin ^2 x}{\cos ^2 x \cdotp \sin ^2 x}dx + \int \frac{\cos ^2 x }{\cos ^2 x \cdotp \sin ^2 x}dx
Semplifichiamo ed otteniamo:
=\int \frac{1}{ \sin ^2 x}dx + \int \frac{1}{ \cos ^2 x}dx
Ora, abbiamo due integrali immediati, perchè possiamo usare le formule seguenti di integrali immediati:
\int \frac{1}{\sin ^2 x}dx = - \cotg x +c
\int \frac{1}{\cos ^2 x}dx = \tg x +c
Usiamo queste formule ed abbiamo risolto l’esercizio!
=- \cotg x + \tg x +c
Esercizio 10. \int \sin ^5 x \; dx
L’obiettivo nostro in questo caso è quello di ricondurci ad integrali immediati del tipo
\int f'(x) [f(x)]^\alpha \; dx =\frac{[f(x)]^{\alpha + 1 }}{\alpha + 1} +c con \alpha \ne -1
dove al posto di f(x) ho o il seno o il coseno. Dobbiamo far comparire all’opposto o un seno o un coseno: se ho un seno elevato a qualcosa devo avere un coseno perchè ne è la derivata, se ho un coseno elevato a qualcosa devo avere un seno vicino che ne è la derivata. Per far ciò scriviamo:
\int \sin ^5 x \; dx=\int \sin ^3 x \cdotp \sin ^2 x \; dx=\int \sin ^3 x \cdotp (1-\cos ^2 x) \; dx=
Spezziamo l’integrale in due.
=\int \sin ^3 x \; dx -\int \sin ^3 x \cos ^2 x \;dx
e facciamo la stessa cosa col seno del primo e con il seno del secondo integrale.
=\int \sin ^2 x \sin x \; dx -\int \sin ^2 x \sin x \cos ^2 x \;dx =\int (1- \cos ^2 x) \sin x \; dx -\int (1- \cos ^2 x) \sin x \cos ^2 x \;dx =
=\int \sin x \; dx- \int \cos ^2 x \sin x \; dx -\int \sin x \cos ^2 x \;dx + \int \sin x \cos ^4 x \;dx
Scriviamoli nella forma dell’integrale immediato \int f'(x) [f(x)]^\alpha \; dx =\frac{[f(x)]^{\alpha + 1 }}{\alpha + 1} +c con \alpha \ne -1
\int \sin x \; dx- 2 \int \sin x [\cos x]^2 \; dx + \int \sin x [\cos x]^4 \;dx
ed applicando la formula abbiamo risolto l’integrale. Ricordiamoci che il primo integrale è quello immediato del seno. Visto che abbiamo a che fare con le derivate del coseno, ricordiamoci che la derivata è il – seno. Quindi dobbiamo moltiplicare e dividere per -1 per far comparire la derivata esplicitamente laddove serva.
\int \sin x \; dx- 2 \int \sin x [\cos x]^2 \; dx - \int -\sin x [\cos x]^4 \;dx
=-\cos x + \frac{2}{3} \cos ^3 x - \frac{1}{5} \cos ^5 x + c
e l’abbiamo risolto! Continuiamo con gli esercizi svolti di integrali!
1. Esercizi svolti integrazione per SOSTITUZIONE
Livello FACILE
Esercizio 11. \int \frac{1 + e^{\sqrt{x} } }{\sqrt{x}} dx
Integrali come questo si possono anche svolgere usando gli integrali immediati direttamente, però se la professoressa ve lo chiede esplicitamente di utilizzare l’integrazione per sostituzione allora eccovi alcuni esempi. Più avanti invece, vedremo integrali che si possono svolgere solamente con la sostituzione. Quindi la sostituzione dovrà essere l’arma finale, se non sapete come svolgere l’integrale. Non ci sono regole fisse su quali sostituzioni in particolare fare, perciò è importante fare esercizi ed imparare più o meno come funzionano! Visto che sono più o meno sempre gli stessi, sarete pronti nella verifica!
In questo caso, quello che possiamo notare è che ci sono due termini di radice uguali. L’idea quindi sarebbe quella di porre \sqrt{x}=t, in questo modo l’integrale diventerebbe \int \frac{1 + e^t}{t} dx, quindi più semplice. Però attenzione! Bisogna anche sostituire il dx. E lo si ricava sempre con questa procedura:
\sqrt{x}=t \implies x=t^2 \implies dx= D(t^2) dt = 2t \; dt
Sostituiamo ed abbiamo un nuovo integrale della forma più semplice!
\int \frac{1 + e^t }{t} 2t \; dt
Ora, è comparsa una t che possiamo semplificare.
2 \int (1 + e^t) dt = 2 \int dt + 2 \int e^t dt
che sono due integrali immediati che già abbiamo risolto. Otteniamo allora:
=2t + 2 e^t + c
Dopo aver risolto l’integrale però bisogna tornare alla variabile dell’inizio, cioè la x. Risostituiamo:
=2 \sqrt{x} + 2 e^{ \sqrt{x}} + c
Esercizio 12. \int \frac{1}{x \sqrt{2x-1} } dx
In questo caso non è immediata la scelta. Quando non lo è voi provate: se vi riesce bene, se vi viene qualcosa di complicato fin da subito provate subito un’altra sostituzione. In questo caso quella vincente è \sqrt{2x-1} = t
E facciamo la stessa procedura di prima per il dt.
\sqrt{2x-1} = t \implies 2x-1 = t^2 \implies x= \frac{t^2}{2} +\frac{1}{2} \implies dx= t \; dt
Sostituiamo il tutto nell’integrale:
\int \frac{1}{x \sqrt{2x-1} } dx =\int \frac{1}{ \frac{t^2 +1}{2} \cdotp t} t \; dt =\int \frac{1}{ \frac{t^2 +1}{2}} dt
=2 \int \frac{1}{ t^2 +1} dt
Ed usando l’integrale immediato \int \frac{1}{ x^2 +1} dx = \arctg x +c otteniamo:
=2 \arctg t +c = 2 \arctg \sqrt{2x-1} +c
Esercizio 13. \int \frac{2 \arctg x + 1}{x^2 + 1} dx
Qui l’idea è che nell’integrale ciò che dà fastidio è l’arcotangente sicuramente. Partiamo da questo allora e proponiamo questa sostituzione: poniamo t= \arctg x
\implies x= \tg t \implies dx=D(\tg t) dt = (1 + \tg ^2 t )dt
Sostituiamo nell’integrale il tutto:
\int \frac{2 \arctg x + 1}{x^2 + 1} dx = \int \frac{2t +1}{\tg ^2 t + 1} (1 + \tg ^2 t )dt
Possiamo adesso semplificare ed avere solo polinomi, è quindi stata una scelta giusta!
=\int (2t+1)dt = 2 \int t \;dt+ \int dt = 2 \frac{t^2}{2} + t +c =t^2 + t +c
Ritorniamo alla variabile x dell’inizio:
= \arctg ^2 x + \arctg x +c
Livello MEDIO
Esercizio 14. \int \frac{2}{\sin x} dx
Quando si ha a che fare con integrali di soli seno e coseno, è quasi sempre la scelta giusta sostituire con le formule parametriche:
t= \tg \frac{x}{2} \implies \sin x= \frac{2t}{1+t^2} e \cos x = \frac{1-t^2}{1+t^2}
E sono utilissime perchè ci permettono di passare dalle funzioni seno e coseno a polinomi. In questo caso utilizziamo la formula parametrica appena scritta del seno, e calcoliamoci il dt.
t= \tg \frac{x}{2} \implies \frac{x}{2} = \arctg t \implies x= 2 \arctg t \implies dx= 2 D(\arctg t ) dt = \frac{2}{1+t^2} dt
Sostituiamo il tutto nell’integrale:
\int \frac{2}{\sin x} dx = \int \frac{2}{\frac{2t}{1+t^2}} \frac{2}{1+t^2} dt
Si può semplificare il 1+t^2 ( quando sono frazioni di frazioni, basta immaginare di capovolgere la frazione al denominatore e metterla all’incontrario sul numeratore e vedere se si può semplificare).
=2 \int \frac{1}{t} dt = 2 \ln |t| +c
Come sempre si ritorna alla variabile iniziale x:
= 2 \ln | \tg \frac{x}{2} | +c
Esercizio 15. \int \frac{1}{\cos x} dx
Anche in questo caso effettuiamo la sostituzione con la formula parametrica dette nell’esercizio precedente:
t= \tg \frac{x}{2} \implies \cos x = \frac{1-t^2}{1+t^2} con dx=\frac{2}{1+t^2} dt
e sostituiamo nell’integrale il tutto:
\int \frac{1}{\cos x} dx =\int \frac{1}{\frac{1-t^2}{1+t^2}} \frac{2}{1+t^2} dt = \int \frac{2}{1-t^2}dt
Adesso, utilizziamo un paio di trucchetti mai detti fino ad adesso. Il primo è scrivere il denominatore come 1-t^2 = (1-t)(1+t) ed il secondo ed importantissimo trucchetto è quello di aggiungere e sottrarre t. Inoltre il 2 lo scriviamo come 1+1 semplicemente, state attenti e leggete con calma!
= \int \frac{1+1+t-t}{(1-t)(1+t)}dt
Ora utilizziamo un altro trucchetto che però abbiamo già usato…quello di spezzare la frazione! E la spezziamo in modo tale che avvengano delle semplificazioni!
=\int \frac{1-t}{(1-t)(1+t)}dt + \int \frac{1+t}{(1-t)(1+t)}dt =\int \frac{1}{1+t}dt + \int \frac{1}{1-t}dt
Ora i due integrali li sappiamo risolvere, utilizziamo la formula dell’integrale immediato seguente:
\int \frac{f'(x)}{f(x)}dx = \ln |f(x)| +c
Segue che:
= \ln |1+t| - \ln |1-t| +c = \ln \frac{1+t}{1-t} +c =\ln \frac{1+\tg \frac{x}{2} }{1-\tg \frac{x}{2} } +c
avendo usato una proprietà del logaritmo che dice che: \ln a - \ln b = \ln \frac{a}{b}.
Continuiamo con gli esercizi svolti di integrali!
Esercizio 16. \int \frac{3}{4 +4 \sin x} dx
Notiamo che la prima cosa che possiamo fare fin da subito è mettere in evidenza il 4 e portarlo fuori. Inoltre essendo che non possiamo immediatamente ricondurlo a nessun integrale fondamentale, allora procediamo per sostituzione con formule parametriche viste anche prima.
\int \frac{3}{4 +4 \sin x} dx= \int \frac{3}{4(1+ \sin x)}=\frac{3}{4} \int \frac{1}{1+ \sin x} dx
Poniamo t= \tg \frac{x}{2} \implies \sin x = \frac{2t}{1+t^2} con dx=\frac{2}{1+t^2} dt
=\frac{3}{4} \int \frac{1}{1+ \frac{2t}{1+t^2}} \frac{2}{1+t^2} dt = \frac{3}{2} \int \frac{1}{\frac{1+t^2 +2t}{1+t^2}}\cdotp \frac{1}{1+t^2} dt
dove fatto il minimo comune multiplo al denominatore. Inoltre possiamo semplificare. Ricaviamo così questo integrale:
=\frac{3}{2} \int \frac{1}{1+t^2 +2t} dt
A questo punto al denominatore abbiamo un polinomio di secondo grado e lo possiamo anche scrivere in una forma più semplice se il Delta è uguale a zero o maggiore di zero. In questo caso è uguale a zero.
Abbiamo t^2 +2t+1. Calcoliamo le soluzioni t_{1,2}= \frac{-b \pm \sqrt{b^2 -4ac}}{2a}=-1
E visto che si può scrivere sempre at^2 +bt + c = (t-t_1)(t-t_2) = (t+1)(t+1)=(t+1)^2
Riscriviamo quindi il nostro integrale.
=\frac{3}{2} \int \frac{1}{(t+1)^2} dt=\frac{3}{2} \int (t+1)^{-2}
Utilizziamo la formula dell’integrale immediato indefinito \int f'(x) [f(x)]^\alpha \; dx =\frac{[f(x)]^{\alpha + 1 }}{\alpha + 1} +c con \alpha \ne -1
Ricaviamo la soluzione:
=- \frac{3}{2} (t+1)^{-1} =- \frac{3}{2} ( \tg \frac{x}{2} +1)^{-1}
Livello DIFFICILE
Esercizio 17. \int \sqrt{1-x^2} dx
Questi ultimi esercizi dell’integrazione per sostituzione sono particolari e da imparare a memoria, e c’è da dire che escono quasi mai nelle verifiche. Questo per esempio è un tipo di integrale della forma \int \sqrt{a^2-x^2} dx e si risolve sempre con la sostituzione di un seno x= \sin t, e ciò si può fare perchè la funzione integranda ha il codominio fra 1 e -1. Quindi avremo che:
x= \sin t \implies dx= \cos t \; dt
Sostituiamo nell’integrale:
\int \sqrt{1-x^2} dx = \int \sqrt{1-\sin ^2 t} \cos t \; dt = \int \cos t \cdotp \cos t \; dt =\int \cos ^2 t dt
Quindi la tattica è stata quella di sfruttare la formula fondamentale della trigonometria e far comparire solo un coseno al quadrato. Il coseno al quadrato ha più risoluzioni. Come detto prima il coseno ed il seno si risolvono quasi sempre con le formule parametriche, ma non qui: il coseno al quadrato si risolve semplicemente usando la formula di bisezione con angolo 2t ed elevandola al quadrato! Cioè:
\cos \frac{\alpha}{2} = \pm \sqrt{\frac{1+ \cos \alpha }{2}}
\cos ^2 \frac{\alpha}{2} = \frac{1+ \cos \alpha }{2}
Poniamo alfa uguale a 2t ed otteniamo la formula per un generico angolo:
\cos ^2 t =\frac{1+ \cos 2t}{2}
Sostituiamo nell’integrale:
=\int \frac{1+ \cos 2t}{2}dt = \frac{1}{2} \int dt + \frac{1}{2} \int \cos 2t dt = \frac{1}{2}t + \frac{1}{4} \sin 2t + c
=\frac{1}{2}t + \frac{1}{2} \sin t \cos t + c = \frac{1}{2}t + \frac{1}{2} \sin t \sqrt{1-\sin ^2 t}+ c =\frac{1}{2} \arcsin x + \frac{1}{2} x \sqrt{1-x^2}+ c.
Esercizio 18. \int \sqrt{9-x^2} dx
Questo integrale è della stessa forma di quello dell’esercizio precedente. Però nella sostituzione cambia della costante moltiplicativa, cioè si pone: x= 3 \sin t \implies dx=3 \cos t \; dt
Così elevato al quadrato ho un 9 vicino al seno e posso mettere in evidenza e portare fuori, ed avrò lo stesso integrale dell’esercizio precedente.
=\int \sqrt{9-(3 \sin t)^2} 3 \cos t \; dt = \int \sqrt{9-9 \sin ^2 t} \cdotp 3 \cos t \; dt =
=\int 3 \int \sqrt{9(1- \sin ^2 t)} \cos t \; dt =\int 3 \sqrt{9} \sqrt{1- \sin ^2 t} \cos t \; dt = 9 \int \cos ^2 t \; dt
ed abbiamo lo stesso identico integrale dell’esercizio precedente moltiplicato per 9.
Esercizio 19. \int \frac{1}{\sqrt{x^2 + 1}}dx
Questo è un integrale la cui forma generica è \int \frac{1}{\sqrt{x^2 \pm a^2}}dx e si risolve con la sostituzione t= x + \sqrt{x^2 \pm a^2 }, quindi come si può notare per niente intuitivo. Facciamo la sostituzione con a=1 e ricaviamo la x e il dx.
t= x + \sqrt{x^2 + 1 } \implies t-x=\sqrt{x^2 +1} \implies t^2 +x^2 -2tx=x^2 +1
2xt = t^2 -1 \implies x= \frac{ t^2 -1}{2t} \implies dx=\frac{t^2 + 1}{2t^2}dt
Quindi:
\int \frac{1}{\sqrt{x^2 + 1}}dx = \int \frac{1}{t-x}\frac{t^2 + 1}{2t^2}dt = \int \frac{1}{t- \frac{ t^2 -1}{2t}}\frac{t^2 + 1}{2t^2}dt =
E facendo il minimo comune multiplo al denominatore troviamo:
= \int \frac{1}{\frac{ t^2 +1}{2t}} \cdotp \frac{t^2 + 1}{2t^2}dt =\int \frac{1}{t}dt= \ln |t| +c = \ln (x + \sqrt{x^2 + 1 }) +c
Esercizio 20. \int \sqrt{x^2 + 9} dx
Anche per gli integrali della forma generale \int \sqrt{x^2 \pm a^2} dx si effettua la stessa sostituzione.
t= x + \sqrt{x^2 \pm a^2 } \implies t=x+ \sqrt{x^2 + 9 } \implies t-x=\sqrt{x^2 + 9 }.
t^2 +x^2 -2xt = x^2 + 9 \implies 2xt=t^2 - 9 \implies x=\frac{t^2 - 9 }{2t}
e, tralasciando a voi i calcoli analoghi a quelli di prima il differenziale dx=\frac{t^2 + 9}{2t^2} dt
Ritorniamo all’integrale. (sostituiamo dopo il dx per comodità)
\int \sqrt{x^2 + 9} dx=\int (t-x) dx = \int (t-\frac{t^2 - 9 }{2t}) dx=\int \frac{t^2 + 9}{2t} \cdotp \frac{t^2 + 9}{2t^2} dt
=\int \frac{t^4 + 18t^2 + 81}{4t^3}dt = \int \frac{t^4 }{4t^3}dt +\int \frac{ 18t^2 }{4t^3}dt +\int \frac{81}{4t^3}dt
E abbiamo tre semplici integrali.
=\frac{1}{4} \int t \; dt + \frac{81}{4} \int (t)^{-3} dt + \frac{18}{4} int \frac{1}{t}dt = \frac{1}{8} t^2 - \frac{81}{8} (t)^{-2} + \frac{18}{4} \ln |t|
=\frac{1}{8} (x+ \sqrt{x^2 + 9 })^2 - \frac{81}{8} (x+ \sqrt{x^2 + 9 })^{-2} + \frac{18}{4} \ln |x+ \sqrt{x^2 + 9 }|
Ecco fatto! Continuiamo con gli esercizi svolti di integrali!
2. Esercizi svolti Integrazione per PARTI
Livello FACILE
Esercizio 21. \int x \ln x \; dx
Quando si integra per parti? Molto spesso si sceglie l’integrazione per parti quando si ha nell’integrale diverse funzioni insieme: per esempio polinomi moltiplicati a logaritmi o seni o coseni ecc. Quindi funzioni diverse e non collegabili direttamente tramite qualche formula. Ricordiamo l’unica formula dell’integrazione per parti:
\int f(x) \cdotp g'(x) \; dx = f(x) \cdotp g(x) - \int f'(x) \cdotp g(x) \; dx
In pratica passiamo dal risolvere l’integrale a primo membro a risolvere l’integrale al secondo membro che deve essere chiaramente più semplice dell’altro. Nell’integrazione per parti una funzione dentro all’integrale viene derivata e l’altra viene integrata. La scelta di quale deve essere derivato e quale integrato deve essere fatta in modo tale che risulti più semplice l’integrale finale, tutto qui. Per capire meglio, ritorniamo subito all’esercizio.
La scelta più intuitiva è scegliere di derivare il logaritmo, perchè farne l’integrale è complicato. Quindi scegliamo f(x)=\ln x e g'(x)=x. Nella formula dell’integrazione per parti, che sta sopra, come possiamo vedere dobbiamo trovare prima f'(x) e g(x):
f(x) = \ln x \implies f'(x)= \frac{1}{x}
g'(x) = x \implies g(x)= \int x \; dx = \frac{1}{2}x^2 (senza mettere già la costante additiva, la si mette alla fine).
Sostituiamo queste quantità nella formula, otteniamo:
\int \ln x \cdotp x \; dx = \ln x \cdotp \frac{1}{2}x^2 - \int \frac{1}{x} \cdotp \frac{1}{2}x^2 \; dx =
= \ln x \cdotp \frac{1}{2}x^2 - \frac{1}{2} \int x \; dx
Come potete vedere ci siamo ricondotti al calcolo di un integrale molto più semplice ed immediato. Troviamo la soluzione:
= \ln x \cdotp \frac{1}{2}x^2 - \frac{1}{4}x^2 +c
Esercizio 22. \int x \; \cos x \; dx
Qui abbiamo un integrale con funzioni completamente diverse fra di loro. Scegliamo di derivare la x così nell’integrale finale scompare e ce lo leviamo da torno, e scegliamo da integrare il coseno.
f(x)=x \implies f'(x)= 1
g'(x)=\cos x \implies g(x)= \int \cos x \; dx = \sin x
Sostituiamo il tutto nella formula.
\int x \cdotp g'(x) \; dx =x \cdotp \sin x - \int 1 \cdotp \sin x \; dx = x \cdotp \sin x + \sin x +c
Per il calcolo dell’integrale basta vedere la tabella degli integrali immediati che sta sopra a tutto da imparare a memoria!
Esercizio 23. \int \frac{x+2}{e^x} dx
Anche in questo caso, come sempre, ci sono funzioni diverse. Per prima cosa grazie ad una proprietà degli esponenziali portiamo la e^x sopra con un segno meno all’esponente. In questo modo eliminiamo la frazione e sarà tutto più intuitivo.
\int \frac{x+2}{e^x} dx = \int (x+2) e^{-x} \; dx
Ora dobbiamo scegliere se derivare (x+2) o e^{-x}. Cosa deriviamo e cosa integriamo? Scegliamo di derivare la (x+2) visto che la derivata è 1 e non ci dà problemi. Anche l’integrale di e^{-x} è semplice ed immediato!
f(x) = (x+2) \implies f'(x)= 1
g'(x) = e^{-x} \implies g(x)= \int e^{-x} dx = - \int -e^{-x}dx = -e^{-x}
Se non sapete come si calcola questo integrale o questi d’ora in poi vedete nel primo capitolo e capirete tutto! Sostituiamo nella formula:
\int (x+2) \cdotp g'(x) \; dx =(x+2) \cdotp (-e^{-x}) - \int 1 \cdotp (-e^{-x}) \; dx=
=-(x+2) \cdotp e^{-x} - \int -e^{-x} \; dx=-(x+2) \cdotp e^{-x} -e^{-x}+c=e^{-x}(-x-2-1) +c = e^{-x}(-x-3) +c
Livello MEDIO
Esercizio 24. \int \ln x \; dx
Qui direte: ma non c’è una sola funzione? E allora come faccio? Piccolo trucchetto: scrivo \ln x come 1 \cdotp \ln x! Anche 1 è una funzione, funzione costante ma comunque una funzione. E scelgo di derivare il logaritmo e di integrare l’uno.
f(x) =\ln x \implies f'(x)= \frac{1}{x}
g'(x) = 1 \implies g(x)= \int dx =x
Sostituiamo nell’integrale come sempre.
\int 1 \cdotp \ln x \; dx =\ln x \cdotp x - \int \frac{1}{x} \cdotp x \; dx =x \ln x - \int dx = x \ln x - x +c
Non dimenticatevi mai alla fine la costante additiva c!
Esercizio 25. \int \ln ^2 x \; dx
Qui l’esercizio prenderà una piega ancora non vista, però andiamo per passi. Analogamente all’esercizio precedente, scriviamo il logaritmo moltiplicato per uno. Anche qui scegliamo di derivare il logaritmo al quadrato ed integrare l’1.
f(x) =\ln ^2 x \implies f'(x)= \frac{2 \ln x}{x}
g'(x) = 1 \implies g(x)= \int dx =x
Ricaviamo usando la formula dell’integrazione per parti:
\int 1 \cdotp \ln ^2 x \; dx =x \ln ^2 x - \int \frac{2 \ln x}{x} \cdotp x \; dx=x \ln ^2 x - 2 \int \ln x \; dx
Siamo ritornati al caso precedente: anche in questo caso l’integrale si deve risolvere integrando nuovamente per parti. Prendiamo un attimo da parte \int \ln x \; dx. Questo lo abbiamo già risolto nel numero 24. quindi non riscriviamo tutto il procedimento e quindi mettiamo solo il risultato:
\int \ln x \; dx = x \ln x - x + c
A questo punto possiamo sostituire questo risultato nel punto dove eravamo arrivati con l’integrale del logaritmo al quadrato.
x \ln ^2 x - 2 \int \ln x \; dx=x \ln ^2 x - 2 \cdotp (x \ln x - x) +c = x \ln ^2 x - 2 x \ln x + 2x + c
Consiglio: la costante c mettetela alla fine e non fatela entrare in nessun calcolo, perchè è una costante e scrivere c o 2c non cambia nulla: sempre una costante rimane ai fini dell’esercizio. Continuiamo con gli esercizi svolti di integrali!
Esercizio 26. \int x^2 \sin x \; dx
La scelta è semplice qui. Scelgo di derivare la x^2 chiaramente, perchè se derivo il seno: la derivata del seno mi dà il coseno e così via e non risolvo nulla e la x^2 aumenta sempre di grado.
f(x) = x^2 \implies f'(x)= 2x
g'(x) = \sin x \implies g(x)= \int \sin x \; dx= - \cos x
Utilizziamo, con queste funzioni, la formula dell’integrazione per parti:
\int x^2 \cdotp \sin x \; dx = - x^2 -\cos x + \int 2x \cos x \; dx
L’integrale nuovo da calcolare è \int 2x \cos x \; dx , il metodo di risoluzione è integrare nuovamente per parti, scegliendo sempre la 2x come la nuova f(x) da derivare e g'(x) il coseno.
f(x) = 2x \implies f'(x)= 2
g'(x) = \cos x \implies g(x)= \int \cos x \; dx= \sin x
Ed abbiamo:
\int 2x \cdotp \cos x \; dx = 2x \cdotp \sin x - \int 2 \cdotp \sin x \; dx = 2x \sin x +2 \cos x +c
Rimettiamo questa quantità nella prima relazione ed abbiamo finito l’esercizio.
- x^2 -\cos x + \int 2x \cos x \; dx =- x^2 -\cos x + ( 2x \sin x +2 \cos x +c)=- x^2 -\cos x + 2x \sin x +2 \cos x +c
Esercizio 27. \int \arcsin x \; dx
Scriviamo l’arcseno come arcseno moltiplicato per 1, come fatto prima!
\int 1 \cdotp \arcsin x \; dx
Scegliamo chiaramente da derivare l’arcseno e da integrare l’1, il contrario non avrebbe senso: integrare l’arcseno non avrebbe senso perchè già stiamo cercando di integrare l’arcseno che non sappiamo fare!
f(x) = \arcsin x \implies f'(x)= \frac{1}{\sqrt{1-x^2}}
g'(x) = 1 \implies g(x)= \int dx= x
Poniamo queste quantità nella formula dell’integrazione per parti:
\int 1 \cdotp \arcsin x \; dx = x \cdotp \arcsin x - \int \frac{1}{\sqrt{1-x^2}} x \; dx
L’integrale che ne è uscito fuori lo sappiamo risolvere dal primo capitolo! Se non lo avete visto andatelo a vedere più sopra! Scriviamo innanzitutto l’integrale nella forma nuova seguente:
\int \frac{1}{\sqrt{1-x^2}} x \; dx = \int x \cdotp (1-x^2)^{-\frac{1}{2}} dx
Lo risolviamo usando l’integrale fondamentale:
\int f'(x) [f(x)]^\alpha \; dx =\frac{[f(x)]^{\alpha + 1 }}{\alpha + 1} +c con \alpha \ne -1
Quindi moltiplichiamo e dividiamo per -2 per far uscire la derivata.
=- \frac{1}{2} \int -2x \cdotp (1-x^2)^{-\frac{1}{2}} dx =- \sqrt{1-x^2} +c
Mettiamo nella relazione totale ed otteniamo la soluzione.
x \cdotp \arcsin x - \int \frac{1}{\sqrt{1-x^2}} x \; dx =x \arcsin x + \sqrt{1-x^2} +c
Livello DIFFICILE
Esercizio 28. \int e^x \sin x \; dx
Questo è un integrale di risoluzione davvero particolare ed unica. Quando si hanno due funzioni di cui una se la derivo o integro rimane più o meno la stessa come e^x ed una che invece, se la derivo o integro, dopo due volte ritorna in sè stessa \sin x, si procede nel modo seguente. Il passaggio importante viene dopo, la scelta della f(x) può essere qualsiasi. Noi scegliamo per esempio:
f(x) = \sin x \implies f'(x)= \cos x
g'(x) = e^x \implies g(x)= \int e^x \; dx = e^x
Segue che:
\int e^x \sin x \; dx = e^x \sin x - \int e^x \cos x \; dx
Ripetiamo il procedimento. In generale la tattica è ripetere l’integrazione per parti fino a quando non ricompare la funzione iniziale. Applichiamo la formula solo all’integrale che compare chiaramente.
f(x) = \cos x \implies f'(x)= - \sin x
g'(x) = e^x \implies g(x)= \int e^x \; dx = e^x
\int e^x \cos x \; dx = e^x \cos x + \int e^x \sin x \; dx
E sostituiamo:
\int e^x \sin x \; dx = e^x \sin x - ( e^x \cos x + \int e^x \sin x \; dx)=e^x \sin x - e^x \cos x -\int e^x \sin x \; dx
Adesso avviene facciamo qualcosa di non intuitivo. Un altro trucchetto utile per il compito! Questa appena scritta, e che ora riscriviamo, è un’uguaglianza:
\int e^x \sin x \; dx =e^x \sin x - e^x \cos x -\int e^x \sin x \; dx
La trattiamo come una specie di equazione, cioè consideriamo come variabile l’integrale stesso e quindi l’integrale al secondo membro lo portiamo a primo membro, come potete vedere:
2 \int e^x \sin x \; dx =e^x \sin x - e^x \cos x =e^x ( \sin x - \cos x)
Ed ora dividendo il tutto per due abbiamo il risultato!
\int e^x \sin x \; dx =\frac{e^x \sin x - e^x \cos x }{2}
Esercizio 29.
Esercizio 30.
Ecco fatto! Continuiamo con gli esercizi svolti di integrali!
3. Esercizi svolti Integrali di funzioni RAZIONALI
Numeratore che è semplicemente la derivata del denominatore
Esercizio 31. \int \frac{x^3 - 1}{x^4 -4x +2} dx
Prima di provare qualsiasi tattica possibile e immaginabile verificate prima che il numeratore sia la derivata del denominatore: questo avviene soprattutto quando il numeratore è di primo grado, cioè qualche costante e basta. Se così fosse si può risolvere l’integrale in un passaggio, applicando l’integrale immediato seguente:
\int \frac{f'(x)}{f(x)} dx = \ln |f(x)| + c
Ed infatti basta moltiplicare e dividere per 4 per ricavare questa forma.
\int \frac{x^3 - 1}{x^4 -4x +2} dx = \frac{1}{4} \int \frac{4(x^3 - 1)}{x^4 -4x +2} dx=
=\frac{1}{4} \int \frac{4x^3 - 4)}{x^4 -4x +2} dx=\ln |x^4 -4x +2| +c
Denominatore di PRIMO grado
Esercizio 32. \int \frac{x+5}{x+3}dx
Quando si ha il denominatore di primo grado e non ci si può ricondurre al fatto che il numeratore sia la derivata del denominatore, allora si effettua la divisione di polinomi. La spiegheremo adesso e non più negli esercizi successivi.
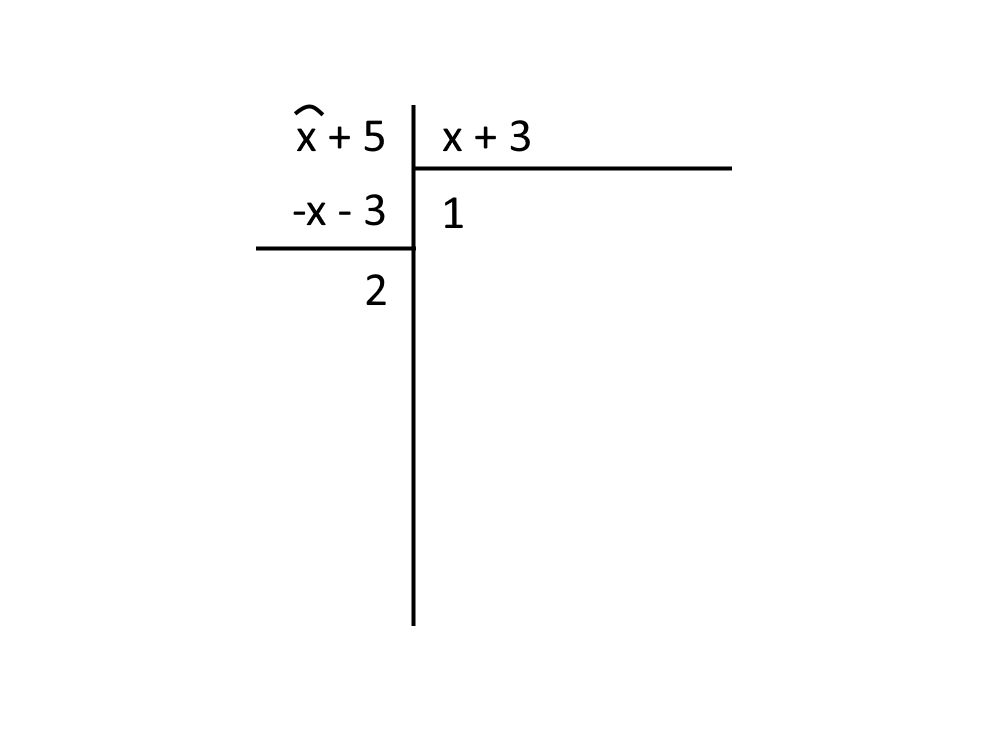
Abbassiamo la x e dividiamola per la x del divisore che fa ovviamente 1 e lo scriviamo. Dopo di che moltiplichiamo questo 1 per il divisore: cioè moltiplichiamo 1 per (x+3) e scriviamo sotto (x+5) il risultato ma cambiato di segno, quindi -x -3. Fatto ciò facciamo la somma di x+5 e di -x -3 che fa ovviamente 2. Quando siamo arrivati ad un numero solo, esso è il resto, mentre 1 è il quoziente.
Una divisione di polinomi fra un numeratore e denominatore può essere scritta come:
\frac{N(x)}{D(x)} = Q(x) + \frac{R(x)}{D(x)}
Quindi nel nostro caso sostituendo il quoziente trovato, il resto ed il denominatore otteniamo:
\frac{x+5}{x+3} = 1 + \frac{2}{x+3} (se fate il mcm come prova ritrovate infatti la frazione iniziale)
Riscriviamolo nell’integrale:
\int (1 + \frac{2}{x+3} )dx = \int dx + 2 \int \frac{1}{x+3}dx = x + \ln |x+3| +c
e siamo ritornati ad una frazione del caso precedente che sappiamo fare!
Esercizio 33. \int \frac{2x^2 -3x +4}{2x - 3}dx
Denominatore di primo grado…divisione di polinomi!
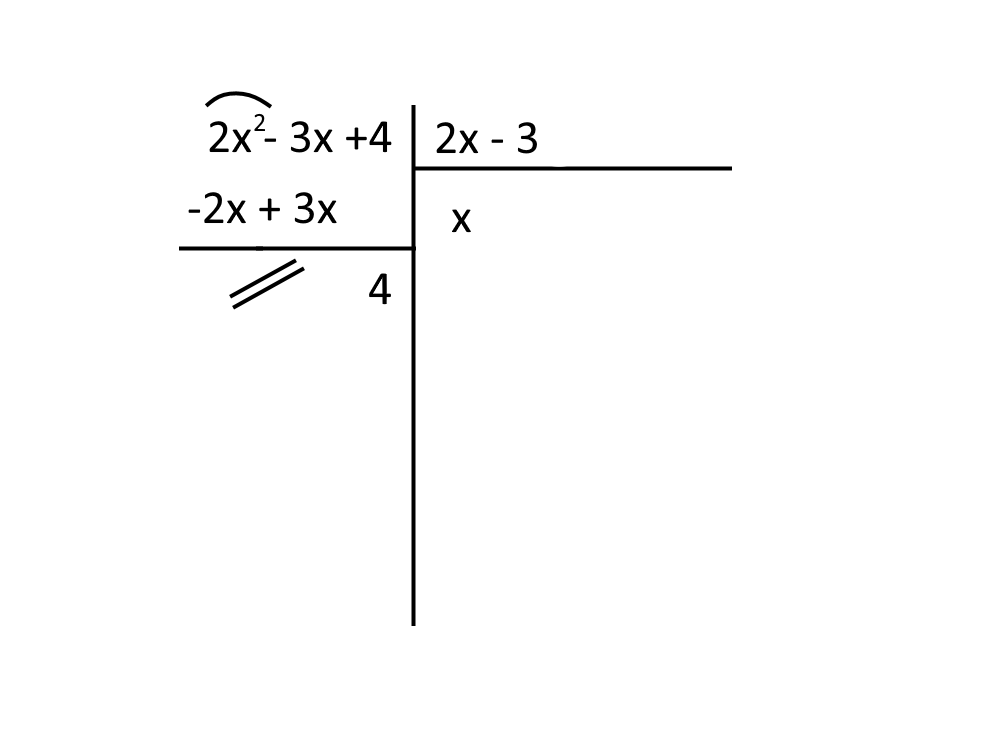
Sostituiamo i dati in \frac{N(x)}{D(x)} = Q(x) + \frac{R(x)}{D(x)}
\frac{2x^2 -3x +4}{2x - 3} = x + \frac{4}{2x-3}
Sostituiamo nell’integrale e spezziamolo.
\int \frac{2x^2 -3x +4}{2x - 3}dx = \int x dx+\int \frac{4}{2x-3}dx =
= \int x dx+2 \int \frac{2}{2x-3}dx = \frac{1}{2}x^2 + 2 \ln |2x-3| +c
Denominatore di SECONDO grado
Questo a sua volta si suddivide in tre casi: discriminante delta positivo, uguale a zero, negativo.
Discriminante positivo >0
Esercizio 34. \int \frac{x-3}{x^2 - x - 2}dx
Chiaramente prima di mostrare il metodo risolutivo, bisogna prima verificare se il numeratore sia la derivata del denominatore ed usare l’integrale fondamentale che abbiamo visto nel 31. Calcoliamo prima il discriminante del denominatore:
\Delta = b^2 - 4ac = 1 +8 = 9
E’ positivo, quindi rientra in questo caso. Il procedimento è il seguente: calcoliamo le soluzioni dell’equazione del denominatore:
x_{1,2}= \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{1 \pm 3}{2} =2,-1
Matematicamente è possibile scrivere x^2 - x - 2 = (x-x_1 )(x-x_2)=(x-2 )(x+1)
Scriviamo la frazione dell’integrale come:
\frac{x-3}{x^2 - x - 2} = \frac{A}{x-2} + \frac{B}{x+1}
dove A e B sono costanti da calcolare. Non serve capire il perchè si possa fare così, questo è un metodo risolutivo, da imparare a memoria! Ovviamente è possibile dimostrarlo, ma a noi non serve per risolvere un integrale. Calcoliamo adesso A e B, facendo il minimo comune multiplo.
\frac{A}{x-2} + \frac{B}{x+1} = \frac{A(x+1) + B(x-2)}{(x-2)(x+1)}=\frac{Ax+A+ Bx-2B)}{x^2 - x - 2}
Mettiamo in evidenza la x e le costanti.
\frac{x(A+B)+(A-2B)}{x^2 - x - 2}
Questa quantità chiaramente deve essere uguale alla frazione iniziale, altrimenti non avrebbe senso!
\frac{x-3}{x^2 - x - 2} = \frac{x(A+B)+(A-2B)}{x^2 - x - 2}
Questa qui sopra è una uguaglianza, quindi i due membri devono essere uguali. Per essere uguali A+B deve essere uguale ad 1 così abbiamo la stessa x del primo membro, e A-2B deve essere uguale a -3. Abbiamo un sistema.
\begin{cases} A+B=1 \\ A-2B = -3 \end{cases} \implies \begin{cases} A=1-B \\ A-2B=-3 \end{cases}
Sostituendo la A=1-B nella seconda equazione, otteniamo:
\begin{cases} A=1-B \\ 1-B -2B = -3 \end{cases} \implies \begin{cases} A=1-B \\ -3B = -4 \end{cases}
E quindi B=\frac{4}{3} \implies A=1-B=1-\frac{4}{3} = - \frac{1}{3}
Dopo tutto questo procedimento possiamo finalmente tornare al nostro integrale!
\int \frac{x-3}{x^2 - x - 2}dx = \int (\frac{A}{x-2} + \frac{B}{x+1} )dx =- \frac{1}{3} \int \frac{1}{x-2} + \frac{4}{3} \int \frac{1}{x+1} dx
=-\frac{1}{3} \ln |x-2| + \frac{4}{3} \ln |x+1| +c
Continuiamo con gli esercizi svolti di integrali!
Esercizio 35. \int \frac{4}{x^2 - 2x}dx
Il numeratore è la derivata del numeratore? No! Allora applichiamo il procedimento delle costanti A e B tale e quale all’esercizio precedente!
\Delta = b^2 - 4ac = 4
x_{1,2}= \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{2 \pm 2}{2} =2,0
Si può scrivere x^2 - 2x = (x-x_1 )(x-x_2)=(x-2 )(x+0)=x(x-2)
Una frazione di polinomi la si può scrivere come:
\frac{4}{x^2 - 2x} = \frac{A}{x} + \frac{B}{x-2}
Facciamo minimo comune multiplo, mettiamo in uguaglianza con la frazione iniziale e vediamo per confronto a quanto devono valere le costanti.
\frac{A}{x} + \frac{B}{x-2}=\frac{A(x-2) + xB}{x(x-2)}=\frac{x(A+B) -2A}{x^2 - 2x)}
Confrontiamo adesso con la frazione originaria.
\frac{4}{x^2 - 2x} =\frac{x(A+B) -2}{x^2-2x)}
\begin{cases} A+B=0 \\ -2A = 4 \end{cases} \implies \begin{cases} A=-B \\ A=-2 \end{cases}
E quindi, visto che A=-B allora la costante B=2. Ritorniamo all’integrale adesso!
\int \frac{4}{x^2 - 2x}dx = \int ( \frac{A}{x} + \frac{B}{x-2} )dx =\int (- \frac{2}{x} + \frac{2}{x-2} )dx =
=-2 \int \frac{1}{x}dx +2 \int \frac{1}{x-2}dx = -2 \ln |x| +2 \ln |x-2| +c
Discriminante nullo =0
Esercizio 36. \int \frac{x}{x^2 -4x +4}dx
Questo è un integrale di funzione razionale, calcoliamo il discriminante delta del denominatore innanzitutto.
\Delta = 16 -16=0 (Delta quarti o Delta normale è la stessa cosa)
Calcoliamo l’unica soluzione dell’equazione di secondo grado:
x_{1,2} = \frac{-b \pm 0}{2a}=\frac{4}{2}=2
e come visto negli esercizi precedenti si può sempre scrivere il polinomio di secondo grado come:
x^2 -4x +4 = (x-x_1 )(x-x_2) =(x-2)(x-2)=(x-2)^2 visto che abbiamo due soluzioni uguali. Riscriviamo in questa forma l’integrale.
\int \frac{x}{x^2 -4x +4}dx = \int \frac{x}{(x-2)^2}dx
Ora utilizziamo un trucchetto già usato in precedenza e che si utilizza praticamente sempre quando il discriminante è zero: aggiungiamo e sottraiamo al numeratore 2 e poi spezziamo la frazione in due.
\int \frac{x}{(x-2)^2}dx = \int \frac{x-2+2}{(x-2)^2}dx = \int \frac{x-2}{(x-2)^2}dx + \int \frac{2}{(x-2)^2}dx
= \int \frac{1}{x-2}dx +2 \int (x-2)^{-2} \; dx
Il trucco di aggiungere e sottrarre il 2 si fa quando si intravede la possibilità di ottenere due frazioni di cui sappiamo risolvere gli integrali! Di fatti questi li sappiamo risolvere, li abbiamo già visti nella tabella degli integrali immediati! Quindi la soluzione è:
=\ln |x-2| - (x-2)^{-1} + c
Esercizio 37. \int \frac{2x-1}{x^2 + 2x +1}dx
Anche qui stesso procedimento: lo possiamo calcolare fin da subito? No, e allora vediamo prima di tutto il discriminante.
\Delta = 4-4=0
Calcoliamo le due soluzioni uguali:
x_{1,2}=\frac{-b }{2a}=\frac{-2}{2}=-1
E scriviamo il polinomio di secondo grado come x^2 + 2x +1 =(x-x_1)(x-x_2)=(x+1)(x+1)=(x+1)^2
Riscriviamo l’integrale ora.
\int \frac{2x-1}{x^2 + 2x +1}dx = \int \frac{2x-1}{(x+1)^2}dx
Il trucco a cui voglio ambire è quello di aggiungere e sottrarre un numero per il quale poi riesco a semplificare una parte del numeratore col denominatore. Aggiungo e sottratto 3. In questo modo:
\int \frac{2x-1}{(x+1)^2}dx = \int \frac{2x-1-3+3}{(x+1)^2}dx = \int \frac{2x+2 -3}{(x+1)^2}dx
Così posso staccare la frazione, e mettendo in evidenza il 2 compare x+1 che posso semplificare. Questa non era semplice quindi rileggete!
\int \frac{2x+2-3}{(x+1)^2}dx=\int \frac{2x+2 }{(x+1)^2}dx-\int \frac{3}{(x+1)^2}dx =\int \frac{2(x+1) }{(x+1)^2}dx-\int \frac{3}{(x+1)^2}dx
=2 \int \frac{1}{x+1}dx -3 \int (x+1)^{-2}dx
Integrali che sono immediati e che sappiamo risolvere, vedendo nella tabella sopra a tutto:
=2 \ln |x+1| +3 (x+1)^{-1} + c
Continuiamo con gli esercizi svolti di integrali!
Discriminante negativo <0
Esercizio 38. \int \frac{1}{x^2 +4x +5}dx
Quando il discriminante è negativo come in questo caso: Delta = 16-20 <0 allora si cerca di ricondurre l’integrale a quello immediato seguente:
\int \frac{f'(x)}{k^2 + [f(x)]^2 } dx = \frac{1}{k} \arctg \frac{f(x)}{k} +c
Per far ciò dobbiamo cercare di riprodurre il quadrato di una funzione f(x). Nel nostro caso abbiamo al denominatore:
x^2 +4x +5 che si avvicina ad un quadrato: cioè x^2 +4x +4 = (x+2)^2
E allora scriviamo il 5 come 4+1.
x^2 +4x +5 = x^2 +4x +4 +1 =(x+2)^2 +1 = 1 + (x+2)^2
e ci siamo ricondotti così al modello che abbiamo all’inizio citato. Di fatti il nostro integrale ora lo scriviamo come:
\int \frac{1}{x^2 +4x +5}dx = \int \frac{1}{1 + (x+2)^2}dx
che si riconduce al modello di integrale immediato (con k=1): \int \frac{f'(x)}{k^2 + [f(x)]^2 } dx = \frac{1}{k} \arctg \frac{f(x)}{k} +c
E quindi abbiamo risolto il nostro integrale! Questo integrale svolto ha come soluzione:
= \frac{1}{k} \arctg \frac{f(x)}{k} +c = \frac{1}{1} \arctg \frac{x+2}{1} +c =\arctg (x+2) +c
Continuiamo con gli esercizi svolti di integrali!
Esercizio 39. \int \frac{2}{9x^2 +4}dx
Il discriminante è minore di zero: \Delta = 0 - 4 \cdotp 9 \cdotp 4 = -144 <0
Quindi lo dobbiamo cercare di ricondurre all’integrale immediato: \int \frac{f'(x)}{k^2 + [f(x)]^2 } dx = \frac{1}{k} \arctg \frac{f(x)}{k} +c
Ma lo abbiamo già di questa forma! Ci manca solo manipolare un attimo il numeratore! Scriviamo innanzitutto l’integrale in questa forma e portando il 2 fuori.
\int \frac{2}{9x^2 +4}dx = \int \frac{2}{2^2 + (3x)^2}dx = 2 \int \frac{1}{2^2 + (3x)^2}dx
Ora c’è bisogno di far comparire la derivata di 3x al numeratore, che è 3. Quindi moltiplichiamo e dividiamo per 3.
=\frac{2}{3} \int \frac{3}{2^2 + (3x)^2}dx = \frac{2}{3} \frac{1}{k} \arctg \frac{f(x)}{k} +c =
=\frac{2}{3} \frac{1}{2} \arctg \frac{3x}{2} +c = \frac{1}{3} \arctg \frac{3x}{2} +c
Continuiamo con gli esercizi svolti di integrali!
Denominatore di grado maggiore del secondo
Esercizio 40. Potete vedere questo caso su Wikipedia.
Ecco risolto!
4. Esercizi svolti Integrali INDEFINITI
Questi 5 esercizi svolti di integrali sono integrali misti, con tutti i metodi di risoluzione visti mischiati. Sono utilissimi anche per l’esame di maturità!
Esercizio 41. \int \frac{1+ \tg x }{1- \tg x }dx
Bisogna sempre cercare di semplificare gli integrali: tenere le tangenti non conviene: scriviamo il tutto come seno e coseno.
\int \frac{1+ \tg x }{1- \tg x }dx =\int \frac{1+ \frac{\sin x }{\cos x} }{1- \frac{\sin x }{\cos x} }dx
Poi facciamo il minimo comune multiplo e vediamo cosa esce.
=\int \frac{ \frac{\cos x + \sin x }{\cos x} }{\frac{\cos x - \sin x }{\cos x} }dx
Semplifichiamo i coseni innanzitutto. Abbiamo quindi:
=\int \frac{\cos x + \sin x }{\cos x - \sin x }dx
E possiamo notare che assomiglia all’integrale fondamentale:
\int \frac{f'(x)}{f(x)} dx = \ln |f(x)| + c
Vediamo se è cosi. Facciamo la derivata del denominatore:
D(\cos x - \sin x) = - \sin x - \cos x
Noi abbiamo questo, ma tutto positivo. Quindi basta moltiplicare e dividere per -1 ed il gioco è fatto!
=- \int \frac{-(\cos x + \sin x )}{\cos x - \sin x }dx = - \int \frac{- \cos x - \sin x )}{\cos x - \sin x }dx =
= - \ln |\cos x - \sin x | +c
Continuiamo con gli esercizi svolti di integrali!
Esercizio 42. \int \frac{1}{e^x + e^{-x} }dx
Non si può mettere in evidenza nulla di che, non possiamo aggiungere o sottrarre qualcosa, o altro. Procediamo per sostituzione quindi! Ricordate che quando non sapete come procedere in alcun modo andate per sostituzione! Poniamo:
e^x = t \implies x=\ln t \implies dx= \frac{1}{t} dt
Sostituiamo nell’integrale:
\int \frac{1}{e^x + e^{-x} }dx =\int \frac{1}{t + t^{-1} }\frac{1}{t} dt = \int \frac{1}{t + \frac{1}{t} }\frac{1}{t} dt
Facciamo il minimo comune multiplo al denominatore adesso.
=\int \frac{1}{ \frac{t^2 +1}{t} }\frac{1}{t} dt
Semplifichiamo il \frac{1}{t} ed otteniamo così:
=\int \frac{1}{ t^2 +1 } dt
Questo è l’integrale immediato che ci porta all’arcotangente:
\int \frac{1}{1 + x^2 } dx = \arctg x +c
Quindi otteniamo la soluzione con la variabile t seguente:
= \arctg t +c = \arctg e^x +c ritornando alla variabile x.
Continuiamo con gli esercizi svolti di integrali!
Esercizio 43. \int \frac{x^5 -x^3 -2x -3}{x^4} dx
La strada che seguiamo è quella di spezzare la frazione in 4, perchè vediamo subito che otteniamo 4 integrali immediatamente risolvibili, quindi è la strada giusta da seguire.
\int \frac{x^5 -x^3 -2x -3}{x^4} dx = \int \frac{x^5}{x^4} dx - \int \frac{x^3}{x^4} dx - \int \frac{2x}{x^4} dx - \int \frac{3}{x^4} dx
Semplifichiamo ed otteniamo 4 semplici integrali riconducibili agli integrali immediati:
\int x^\alpha \; dx =\frac{x^{\alpha + 1 }}{\alpha + 1} +c con \alpha \ne -1
e \int \frac{1}{x}dx = \ln |x| + c
Abbiamo quindi 4 termini, per la quale portiamo le costanti al numeratore fuori dagli integrali:
=\int x \; dx - \int \frac{1}{x} dx -2 \int x^{-3} dx -3 \int x^{-4} dx =
=\frac{1}{2} x^2 - \ln |x| + x^{-2} + x^{-3} +c
Continuiamo con gli esercizi svolti di integrali!
Esercizio 44. \int \frac{1+ \cos ^2 x}{\sin 2x} dx
Come sempre, bisogna semplificare la forma dell’integrale. Portare avanti il seno di 2x non ha senso. Utilizziamo quindi la formula di duplicazione: \sin 2x = 2 \sin x \cos x
\int \frac{1+ \cos ^2 x}{\sin 2x} dx = \int \frac{1+ \cos ^2 x}{2 \sin x \cos x } dx
Quando c’è il seno ed il coseno la presenza dell’1 deve sempre portare alla mente la formula:
\sin ^2 x+ \cos ^2 x = 1 e la inseriamo.
\int \frac{\sin ^2 x+ \cos ^2 x+ \cos ^2 x}{2 \sin x \cos x } dx =\int \frac{\sin ^2 x+2 \cos ^2 x}{2 \sin x \cos x } dx
Spezziamo la frazione in due più semplici, così da arrivare a delle semplificazioni.
= \int \frac{\sin ^2 x}{2 \sin x \cos x } dx + \int \frac{2 \cos ^2 x}{2 \sin x \cos x } dx =\frac{1}{2} \int \frac{\sin x}{ \cos x } dx + \int \frac{ \cos x}{ \sin x } dx
E ci siamo ricondotti al modello: \frac{f'(x)}{f(x)}dx = \ln | f(x) | +c
Nel secondo termine ce l’abbiamo, nel primo invece dobbiamo moltiplicare e dividere per –1 essendo la derivata -seno.
=-\frac{1}{2} \int \frac{- \sin x}{ \cos x } dx + \int \frac{ \cos x}{ \sin x } dx = -\frac{1}{2} \ln | \cos x | + \ln | \sin x | +c
Continuiamo con gli esercizi svolti di integrali!
Esercizio 45. \int x \frac{e^x + e^{-x} }{1+ e^{2x} }dx
Notiamo che l’integrale è una funzione x moltiplicata per una che contiene solo esponenziali. La x ci dà fastidio, e con la formula dell’integrazione per parti la potremmo levare da mezzo, se sappiamo risolvere poi l’integrale con i soli esponenziali. Poniamo allora:
f(x)=x \implies f'(x)=1
g'(x)=\frac{e^x + e^{-x} }{1+ e^{2x} } \implies g(x)= \int \frac{e^x + e^{-x} }{1+ e^{2x} }dx
La g(x) la calcoliamo procedendo per sostituzione. Poniamo:
e^x = t \implies x= \ln t \implies dx = \frac{1}{t}dt
g(x)= \int \frac{e^x + e^{-x} }{1+ e^{2x} }dx = \int \frac{t + t^{-1} }{1+ t^2 } \frac{1}{t}dt
e poi facciamo il minimo comune multiplo al numeratore
=\int \frac{t + \frac{1}{t} }{1+ t^2 } \frac{1}{t}dt = \int \frac{ \frac{t^2 + 1}{t} }{1+ t^2 } \frac{1}{t}dt
Semplifichiamo t^2 +1 ed otteniamo:
= \int \frac{1}{t} \frac{1}{t}dt =\int \frac{1}{t^2} dt = \int t^{-2} dt = - t^{-1} = - e^{-x}=g(x)
Ora che abbiamo calcolato anche la g(x) possiamo applicare la formula dell’integrazione per parti all’integrale dell’esercizio!
\int x \cdotp g'(x) \; dx = -x e^{-x} - \int -e^{-x} \; dx =-x e^{-x} - e^{-x}
Continuiamo con gli esercizi svolti di integrali!
5. Esercizi SVOLTI Integrali DEFINITI
Esercizio 46. \int_2 ^5 (x+1)dx
L’integrale definito serve per calcolare l’area fra il grafico e l’asse x che la funzione ricopre. Quindi se il problema vi chiede quanta area ricopre alla fine va messo il modulo. Se non vi dice nulla come in questo esercizio allora si procede normalmente. L’integrale definito è semplicemente un integrale che va calcolato come un integrale indefinito. La differenza sta nel fatto che gli estremi di integrazione ci danno il valore esatto della costante c. Calcoliamo quindi innanzitutto l’integrale.
\int_2 ^5 (x+1)dx = \int_2 ^5 x \; dx + \int_2 ^5 dx = \frac{1}{2}x^2 |_2 ^5 + x|_2 ^5
Quel simbolo | fra 2 e 5 significa che al posto della x ci dobbiamo mettere l’estremo superiore 5 e poi col segno meno sostituiamo il 2. Vedete qui per capire:
\frac{1}{2}x^2 |_2 ^5 + x|_2 ^5 =( \frac{1}{2}5^2 - \frac{1}{2}2^2 )+ (5-2) = \frac{25}{2} - 2+3= \frac{25}{2}+1
Esercizio 47. Si può calcolare l’integrale definito seguente? \int_{-1} ^1 \frac{1}{x} dx
L’integrale definito per esistere ed essere calcolato c’è bisogno che sia rispettata una condizione: la funzione integranda deve essere continua nell’intervallo di integrazione.
In questo caso quindi dobbiamo verificare che nell’intervallo chiuso [-1,1] la funzione integranda \frac{1}{x} sia continua. La funzione non è continua, perchè in x=0 c’è un asintoto verticale, e di conseguenza un punto di discontinuità.
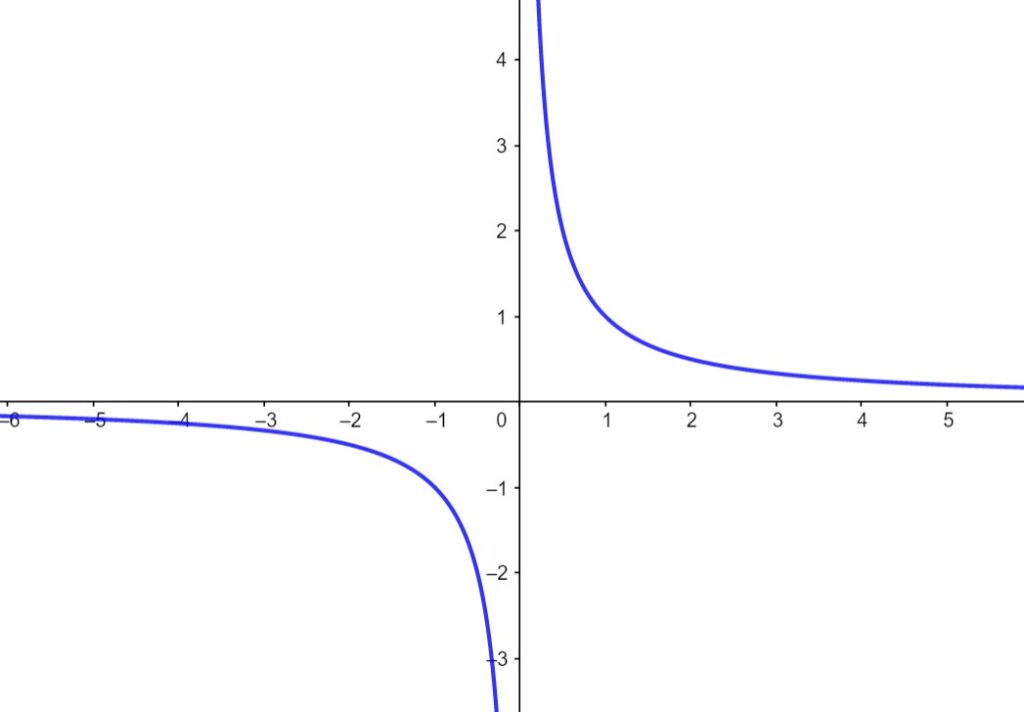
Questo integrale definito quindi non esiste.
Esercizio 48. \int_0 ^{\frac{\pi}{2}} (\sin x + \cos x )dx
Suddividiamo l’integrale in due pezzi.
\int_0 ^{\frac{\pi}{2}} (\sin x + \cos x )dx =\int_0 ^{\frac{\pi}{2}} \sin x \; dx + \int_0 ^{\frac{\pi}{2}} \cos x \; dx
Integrali semplici, la cui soluzione è:
=-\cos x|_0 ^{\frac{\pi}{2}} + \sin x |_0 ^{\frac{\pi}{2}} = (-\cos \frac{\pi}{2} - (- \cos 0)) + (\sin \frac{\pi}{2} - \sin 0 ) =
[katex]=(0-(-1)+(1-0)=2
Continuiamo con gli esercizi svolti di integrali!
Esercizio 49. Calcola l'area che ricopre la funzione -x fra nell'intervallo [3,5].
Dobbiamo quindi calcolare l'integrale definito \int_{3} ^5 -x \; dx e poi il risultato metterlo in modulo assoluto, poichè l'area è una quantità definita positiva.
\int_{3} ^5 -x \; dx = -\frac{1}{2}x^2 |_{3} ^5 = (-\frac{1}{2}5^2 - (-\frac{1}{2}3^2))=
=-\frac{25}{2} + \frac{9}{2} = - \frac{16}{2}
ed infine dobbiamo mettere il risultato in valore assoluto. Quindi A=|- \frac{16}{2}| = \frac{16}{2} !
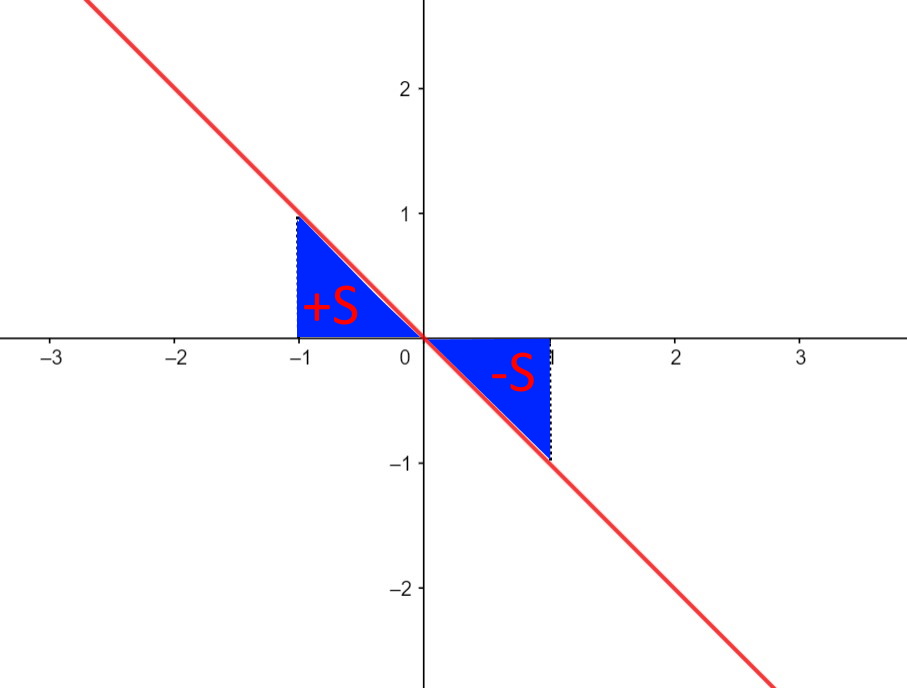
Esercizio 50. Senza fare nessun calcolo quanto vale l'integrale definito seguente?
\int_{-1} ^1 x \; dx
La funzione integranda è una funzione dispari, cioè una funzione simmetrica rispetto l'origine, e quindi ricopre superfici S e -S opposte ed uguali a destra e sinistra come in figura. La somma è quindi zero. Questo ovviamente quando gli estremi di integrazione sono uguali ma di segno opposto.
6. Regole e Consigli per risolvere qualsiasi INTEGRALE

Continuate a studiare sul nostro sito! Non solo esercizi svolti di integrali! Tante altre centinaia di esercizi svolti di matematica che altro ancora!
derivate
continua